Funções Condicionalmente Definidas
Um exemplo
Será que o esboço abaixo representa o gráfico de uma função $f:\mathbb{R}\rightarrow \mathbb{R}$ ?
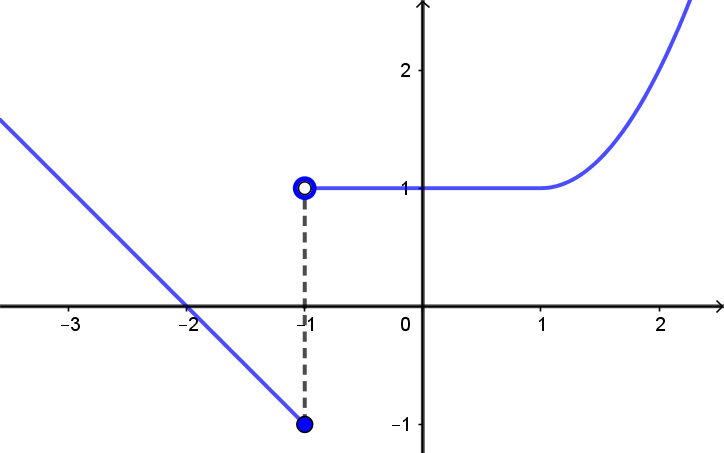
Lembre-se de que, para que o esboço represente o gráfico de uma função $f:\mathbb{R}\rightarrow \mathbb{R}$, para cada valor de $x \in \mathbb{R}$ deve haver um único ponto valor de $y \in \mathbb{R}$ tal que $(x,y)$ seja um ponto deste gráfico. Neste caso, teremos que $f(x) = y$.
Em termos geométricos, isto significa que toda reta vertical deverá cortar o esboço em um ponto e apenas um ponto.
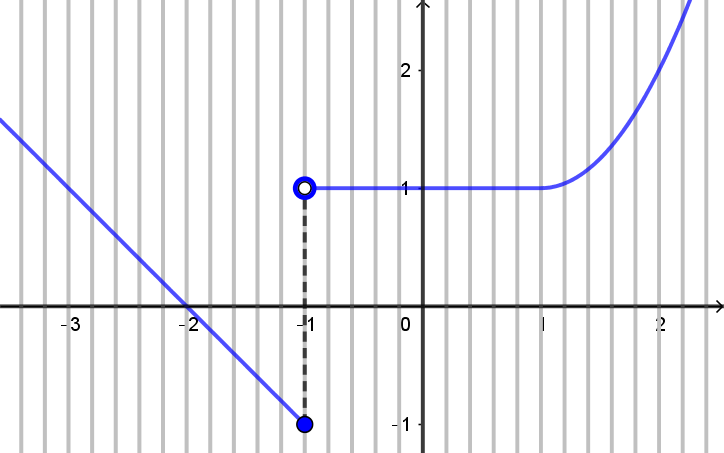
Podemos ver claramente que é isso o que ocorre no esboço apresentado. Você pode ficar com alguma dúvida com relação ao que acontece para $x=-1$, afinal, neste valor de $x$ há um "salto" na função. Note, porém, que o ponto $(-1,-1)$ pertence ao gráfico (o ponto está representado como uma "bolinha cheia"), enquanto o ponto $(-1,1)$ não pertence (o ponto está representado por uma "bolinha vazia"). Com isso, temos $f(-1) = -1$.
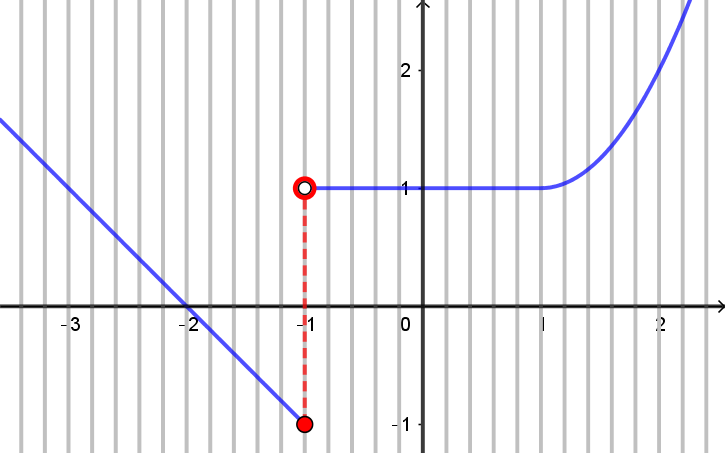
Será que podemos apresentar uma expressão $f(x)$ para esta função, isto é, obter uma expressão que dê explicitamente o valor que a função assume para cada valor de $x \in \mathbb{R}$? Isto depende das informações que temos sobre o gráfico.
Vamos supor que ele seja formado por pedaços de retas para $x \leqslant -1$ e para $-1 < x < 1$, e uma por parábola de vértice $(1,1)$ e concavidade para cima, para $x \geqslant 1$.
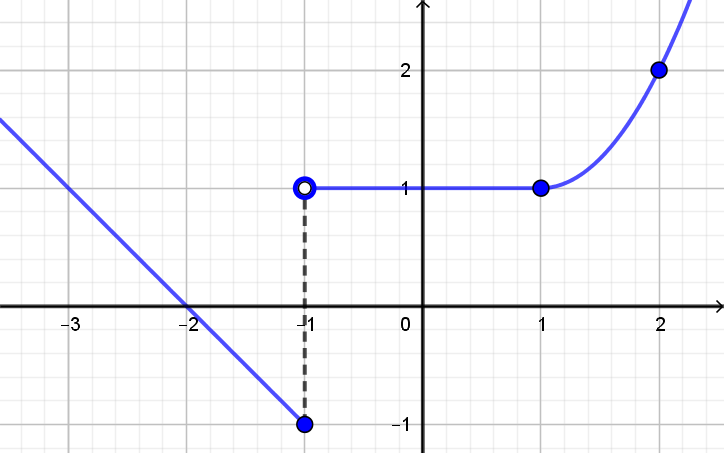
Esta função é
afim, com $f(-2)=0$ e $f(-1)=-1$, para $x\leqslant -1$.
constante e igual a 1, se $-1 < x < 1$.
e quadrática, com vértice $(1,1)$ e $f(2)=2$, quando $x \geqslant 2$.
Com isso, conseguimos obter uma expressão para a função em cada uma das condições acima.
$x\leqslant -1$:
\[b = \frac{\Delta y}{\Delta x} = \frac{y_1 - y_0}{x_1 - x_0} = \frac{-1 - 0}{-1 - (-2)} = \frac{-1}{1} = -1.\]
Nesta condição, a expressão da função será da forma $f(x) = bx + c$. Os pontos $(x_0, y_0) = (-2,0)$ e $(x_1,y_1) = (-1,-1)$ pertencem ao gráfico da função, portantoAssim, temos $y = f(x) = -x + c$. Substituindo $(-1,-1)$, temos
\[-1 = -(-1) + c \therefore c = -2.\]Portanto, $f(x) = -x-2$, se $x \leqslant -1$.
$-1 < x < 1$: Nesta condição, a função $f$ é constante e igual a 1. Assim, sua expressão é dada por $f(x) = 1$.
$x \geqslant 1$: Nesta condição, $f$ é quadrática, logo $f(x)=ax^2+bx+c$. O vértice é dado por
\[\left(-\frac{b}{2a},-\frac{\Delta}{4a}\right) = (1,1),\]logo
\[-\frac{b}{2a} = 1 \therefore b = -2a,\]e
\[-\frac{\Delta}{4a} = 1 \therefore -\frac{(-2a)^2-4ac}{4a} = 1 \therefore -\frac{4a^2-4ac}{4a} = 1 \therefore -\frac{4a(a-c)}{4a} = 1 \therefore -(a-c) = 1 \therefore c-a = 1\]
\[\therefore c=a+1.\]Com isso, a expressão é da forma
\[f(x) = ax^2 - 2ax + a+1.\]Substituindo o ponto $(2,2)$, temos
\[2 = a\cdot 2^2 - 2a\cdot 2 + a+1 \therefore 4a - 4a + a + 1 = 2 \therefore a = 1.\]Com isso, $b=-2a=-2$ e $c= a+1 = 2$, logo $f(x) = x^2-2x+2$, para $x \geqslant 1$.
Obtivemos uma expressão para a função $f$ em cada condição, mas como podemos reunir todas estas possibilidades em uma única expressão? Podemos escrever na forma
\[ f(x) = \begin{cases} -x-2, & \text{se } x \leqslant -1\\ 1, & \text{se } -1 < x < 1\\ x^2 - 2x + 2, & \text{se } x \geqslant 1 \end{cases} \]
Este tipo de escrita é chamado de condicional, e a função é dita condicionalmente definida, ou função partida. Note que estamos dizendo, claramente, como calcular o valor de $f(x)$ em todo os pontos $x$ do domínio $\mathbb{R}$ da função, pois
\[\mathbb{R} = \{x \in \mathbb{R}: x \leqslant -1\} \cup \{x \in \mathbb{R}: -1 < x < 1\} \cup \{x \in \mathbb{R}: x \geqslant 1\}.\] Além disso, para cada valor de $x \in \mathbb{R}$, há um único valor atribuído a $f(x)$, pois não há $x$ que esteja em duas condições diferentes. Mais abaixo, veremos que até seria "permitido" que um mesmo $x$ satisfizesse duas condições, desde que o valor da $f$ fosse igual em ambas.
O valor de $f(x)$ mudaria em algum valor de $x$ se, em vez da expressão acima, escrevêssemos o que se segue? (As mudanças em relação ao exemplo anterior estão em vermelho)
\[ f(x) = \left\{\begin{array}{lll} -x-2, & \text{se } x \leqslant -1\\ 1, & \text{se } -1 < x\;{\color{red}\leqslant}\;1\\ x^2 - 2x + 2, & \text{se } x\;{\color{red}>}\;1 \end{array}\right. \] Repare que $x=1$ agora satisfaz a segunda condição e não mais a primeira. Avaliando $x=1$ de acordo com a segunda condição, temos
Por outro lado, com a expressão que obtivemos anteriormente, o $x=1$ deveria ser avaliado de acordo com a terceira condição, e teríamos
\[ f(x) = \left\{\begin{array}{lll} -x-2, & \text{se } x \leqslant -1\\ 1, & \text{se } -1 < x\;{\color{red}<}\;1\\ x^2 - 2x + 2, & \text{se } x\;{\color{red}\geqslant}\;1 &{\color{red} \Rightarrow f(1) = 1^2 - 2\cdot 1 + 2 = 1.} \end{array}\right. \] Ou seja, a mudança feita não alteraria os valores $f(x)$ da função. São, portanto, expressões diferentes para a mesma função.
E se, agora, escrevêssemos da forma abaixo?
Note que agora trocamos a condição satisfeita pelo $x=-1$. Ele agora satisfaz a segunda condição, e não mais a primeira. Avaliando $x=-1$, temos
\[ f(x) = \left\{\begin{array}{lll} -x-2, & \text{se } x\;{\color{red}\leqslant} -1 &{\color{red} \Rightarrow f(-1) = -1}\\ 1, & \text{se } -1\;{\color{red}<}\;x < 1\\ x^2 - 2x + 2, & \text{se } x \geqslant 1. \end{array}\right. \]Por outro lado, na primeira expressão, antes da mudança, teríamos
\[ f(x) = \left\{\begin{array}{lll} -x-2, & \text{se } x\;{\color{red}<}\;-1\\ 1, & \text{se } -1\;{\color{red}\leqslant}\;x < 1 & {\color{red} \Rightarrow f(-1) = 1}\\ x^2 - 2x + 2, & \text{se } x \geqslant 1. \end{array}\right. \] Ou seja, a alteração feira mudou a função, uma vez que o valor $f(x)$ mudou para pelo menos um valor de $x$. Assim, seriam funções diferentes.
E será que poderíamos definir a função como abaixo?
Repare que $x=1$ satisfaz duas condições, a segunda e a terceira.
Não seria usual escrever desta forma, mas poderíamos sim. O único valor de $x \in \mathbb{R}$ que satisfaz duas condições é o $x=1$, sendo $f(1)$ avaliado com o mesmo valor nestas duas condições. Mas não poderíamos definir a função como abaixo
pois $x=1$ satisfaz à primeira e à segunda condições, tendo valores diferentes em cada uma. Na primeira, temos $f(-1)=-1$ e, na segunda, $f(-1)=1$. Assim, a função não estaria bem definida para $x=-1$.
Funções Condicionalmente Definidas
Uma função $f: \mathrm{D} \rightarrow \mathbb{R}$ é dita condicionalmente definida ou partida se sua expressão é apresentada na forma
\[f(x) = \begin{cases} f_1(x),& \text{se } \text{condição}_1 \\f_2(x),& \text{se } \text{condição}_2\\ \;\;\vdots\\f_n(x),& \text{se } \text{condição}_n \end{cases} \]Sendo
\[\mathrm{D} = \{x \in \mathbb{R}: x\;\textnormal{satisfaz a } \text{condição}_1\} \cup \{x \in \mathbb{R}: x\;\textnormal{satisfaz a } \text{condição}_2\} \cup \ldots \cup \{x \in \mathbb{R}: x\;\textnormal{satisfaz a } \text{condição}_n\}\]Além disso, se um mesmo $x_0 \in \mathrm{D}$ satisfaz a mais de uma condição diferente, por exemplo, $\text{condição}_i$ e $\text{condição}_j$, então $f_i(x_0) = f_j(x_0)$. O mais usual, porém, é que todos os valores de $x \in\mathrm{D}$ satisfaçam apenas uma das condições.

