O Módulo de um Número Real
Você deve se lembrar que, dado um número real, seu módulo ou valor absoluto é o próprio número, caso ele seja positivo ou zero, e seu simétrico positivo, caso o número seja negativo. Além disso, o módulo de 0 é 0.
Assim, por exemplo,
- $|0| = 0$
- $|2| = 2$
- $|-2|= 2 = -(-2)$
- $|\sqrt{2}-1|= \sqrt{2} -1$, pois $\sqrt{2} - 1 > 0$
- $|1 - \sqrt{2}|= \sqrt{2} -1$, pois $1 - \sqrt{2} < 0$, portanto sua "versão positiva" é o $-(1-\sqrt{2}) = \sqrt{2}-1$.
- $|\pi - 3,\!14| = \pi - 3,\!14$, pois $\pi - 3,\!14 > 0$
Como escrever a expressão $|x^2+1|$ sem o módulo?
Note que, pelo que foi visto em funções quadráticas, $x^2 + 1 > 0$ para todo $x\in \mathbb{R}$, portanto $|x^2+1| = x^2+1$.
Formalizando a definição de módulo para números reais, o módulo de $x \in \mathbb{R}$ é dado por
\[|x| = \begin{cases} x,& \text{se } x \geqslant 0\\-x,& \text{se } x < 0. \end{cases} \]Poderíamos também ter definido a o módulo de outras duas outras maneiras, que serão equivalentes:
\[\displaystyle |x| = \begin{cases} x,& \text{se } x > 0\\ 0, & \text{se } x = 0\\-x, & \text{se } x < 0 \end{cases} \;\;\;\;\;\; \displaystyle |x| = \begin{cases} x,& \text{se } x > 0\\-x, & \text{se } x \leqslant 0 \end{cases} \] A diferença entre as definições está apenas em como vamos avaliar o $x=0$. Mas observe que, em todas elas, independentemente da expressão que utilizemos para avaliar $|0|$, teremos 0 como resultado. E qual devemos usar? A mais conveniente à situação estudada, é claro!
Repare que o valor do módulo, isto é, $|x|$, será sempre um número positivo ou 0, sendo $|x|=0$ apenas quando $x=0$.
Neste ponto, é possível que você esteja estranhando uma coisa... Se
como pode, na terceira condição, termos $|x|=-x$, se o módulo é sempre positivo ou zero? Como pode o resultado do módulo ser $-x$? Mas repare que $|x|=-x$ apenas quando $x < 0$. Neste caso, como $x<0$, teremos que $-x > 0$, ou seja, $|x|=-x>0$. Ainda não ficou claro? Vejamos um exemplo. Se $x=-1$, como $x<0$, teremos $|x| = -x = -(-1) = 1$, ou seja, $|-1| = 1$.
Não se engane com o sinal; a expressão $-x$ não é necessariamente um número negativo. Ela será positiva se o $x$ for negativo.
Entre as várias propriedades do módulo, podemos agora destacar duas, que utilizaremos bastante:
- $|x| \geqslant 0, \forall x \in \mathbb{R}$. Além disso, $|x| = 0 \Leftrightarrow x = 0$.
- $|-x|=|x|, \forall x \in \mathbb{R}$
No final deste texto, apresentarmos mais algumas propriedades importantes do módulo.
Como escrever a expressão $|x-1|$ sem o módulo?
Não podemos afirmar o sinal de $x-1$, uma vez que este pode ser positivo, caso $x > 1$, negativo, quando $x < 1$, ou a expressão pode assumir valor 0, caso $x=1$.
Assim, $|x-1|$ depende do valor de $x$, e será dado por
que, pode ser reescrito como
\[|x-1| = \begin{cases} x-1, &\text{se } x \geqslant 1\\-x+1, &\text{se } x < 1 \end{cases} \]
Função Modular
Vamos agora definir a função modular.
A função modular é definida por $f: \mathbb{R} \rightarrow \mathbb{R}$ tal que
\[f(x)=|x| = \begin{cases} \;\;\,x,& \text{se } x \geqslant 0\\-x, & \text{se } x < 0. \end{cases} \]
O gráfico desta função está sobre a reta $y=-x$ quando $x < 0$, e sobre a reta $y=x$ quando $x \geqslant 0$.
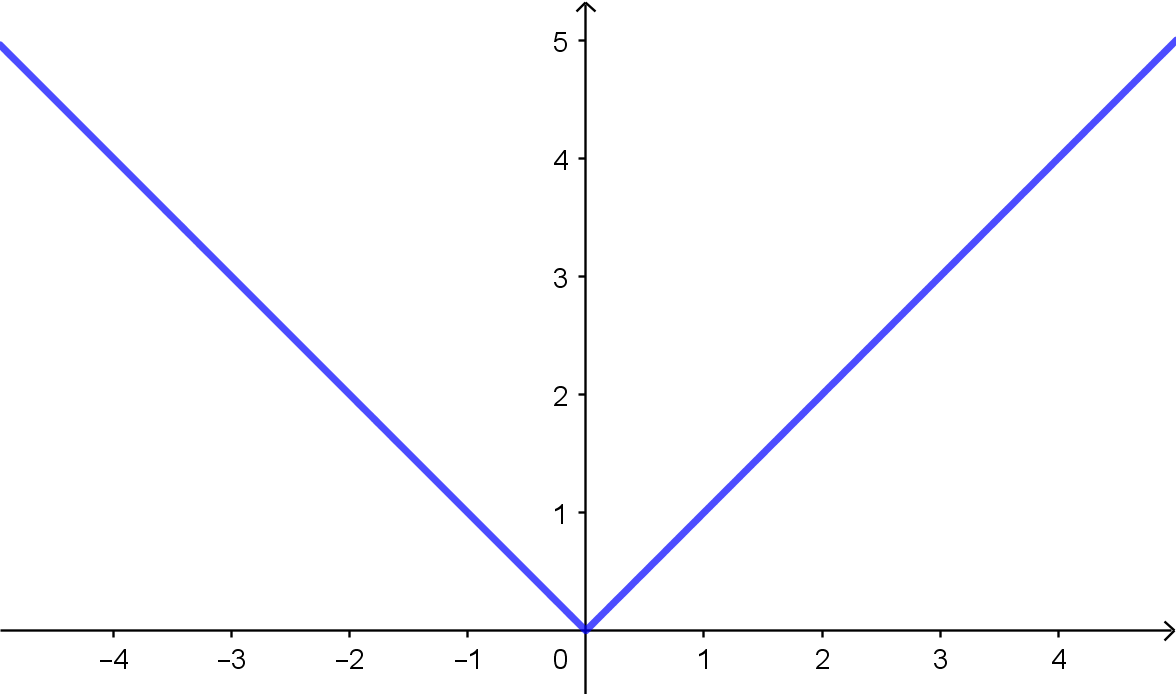
A partir do gráfico da função modular, é fácil percebermos algumas de suas propriedades.
A função modular $f: \mathbb{R} \rightarrow \mathbb{R}, f(x) = |x|$ possui as seguintes propriedades:
- $f(x) \geqslant 0, \forall x \in \mathbb{R}$. Além disso, $f(x) = 0 \Leftrightarrow x = 0$.
- A imagem de $f$ é $[0, +\infty)$
- $f(-x) = f(x), \forall x \in \mathbb{R}$ ($f$ é uma função par)
- $f$ é crescente em $[0, +\infty)$ e decrescente em $(-\infty, 0]$
Apresentar uma expressão para a função $f:\mathbb{R} \rightarrow \mathbb{R}$ definida por
\[f(x) = |x^2-1|,\]sem utilizar módulos e, depois, esboçar seu gráfico.
Pela definição de módulo,
\[|x^2-1| = \begin{cases} x^2-1, & \text{se } x^2-1 \geqslant 0\\ -(x^2-1), & \text{se } x^2-1 < 0 \end{cases} \]Lembre se que a expressão $x^2-1$ é negativa entre suas raízes, $-1$ e $1$, e positiva fora destas raízes, pois $y=x^2-1$ representa a parábola esboçada abaixo.
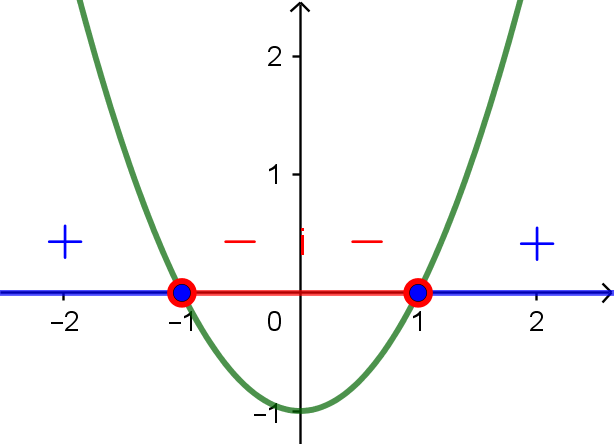
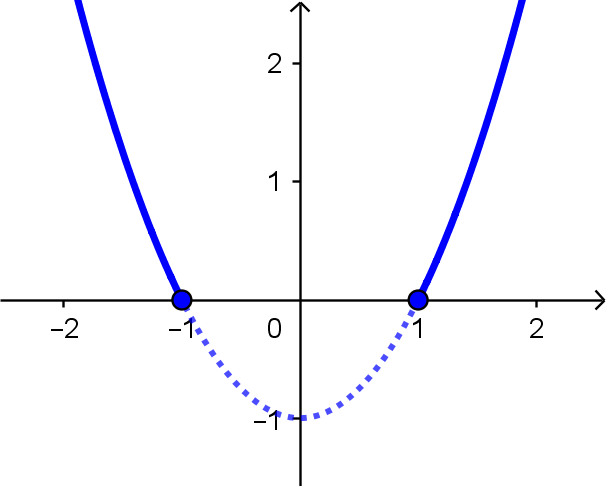
Com isso,
\[|x^2-1| = \begin{cases} x^2-1, & \text{se } x \leqslant -1 \text{ ou } x \geqslant 1 \\ -x^2+1, & \text{se } -1 < x < 1. \end{cases} \]Para $x \leqslant -1$ ou $x \geqslant 1$, temos então $f(x) = x^2-1$, logo seu gráfico será o da função quadrática de expressão $x^2-1$.
Para $-1 < x < 1$, temos $f(x) = - x^2+1$, logo seu gráfico será o da função quadrática de expressão $-x^2+1$.
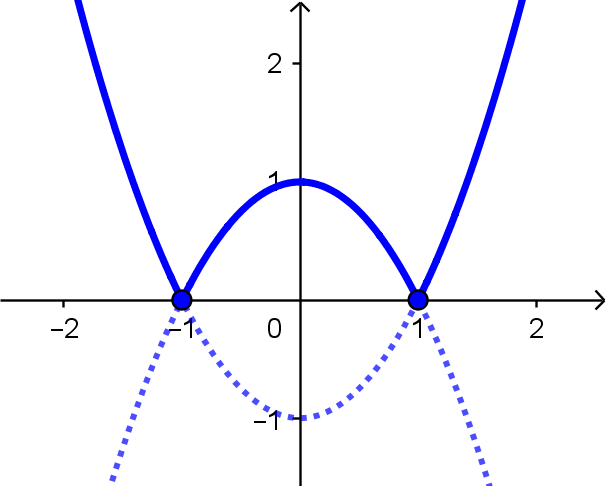
Apresentar uma expressão para a função $f:\mathbb{R} \rightarrow \mathbb{R}$ definida por
\[f(x) = |x-1|+|x+2|,\] sem utilizar módulos e, depois, esboçar seu gráfico.
Observe que
\[|x-1|= \begin{cases} x-1, &\text{se } x-1\geqslant 0\\ -(x-1),& \text{se } x-1 < 0 \end{cases} = \begin{cases} x-1, &\text{se } x\geqslant 1\\ -x+1,& \text{se } x<1, \end{cases} \]e
\[|x+2|= \begin{cases} x+2, &\text{se } x+2\geqslant 0\\ -(x+2),& \text{se } x+2 < 0 \end{cases} = \begin{cases} x+2, &\text{se } x\geqslant -2\\ -x-2,& \text{se } x<-2, \end{cases} \]Assim, vamos dividir o estudo da função $f$ em três possibilidades de valores para $x\in\mathbb{R}$.
$x < -2$: Para $x < -2$, temos $|x-1|=-x+1$ e $|x+2|=-x-2$. Logo
\[f(x) = (-x+1) + (-x-2) = -2x-1, \text{ para } x < -2.\]$-2 \leqslant x < 1$: Para $-2 \leqslant x < 1$, temos $|x-1|=-x+1$ e $|x+2|=x+2$. Logo
\[f(x) = (-x+1) + (x+2) = 3, \text{ para } -2 \leqslant x < 1.\]$x \geqslant 1$: Para $x \geqslant 1$, temos $|x-1|=x-1$ e $|x+2|=x+2$. Logo
\[f(x) = (x-1) + (x+2) = 2x+1, \text{ para } x \geqslant 1.\]
Reunindo as informações,
\[f(x) = |x-1|+|x+2| = \begin{cases} -2x-1, &\text{se } x < -2\\ 3, &\text{se } -2 \leqslant x < 1\\ 2x+1, &\text{se } x \geqslant 1. \end{cases} \]

Equações e inequações modulares
As propriedades da função modular podem ser utilizadas na solução de diversas equações e inequações modulares com as quais podemos nos deparar.
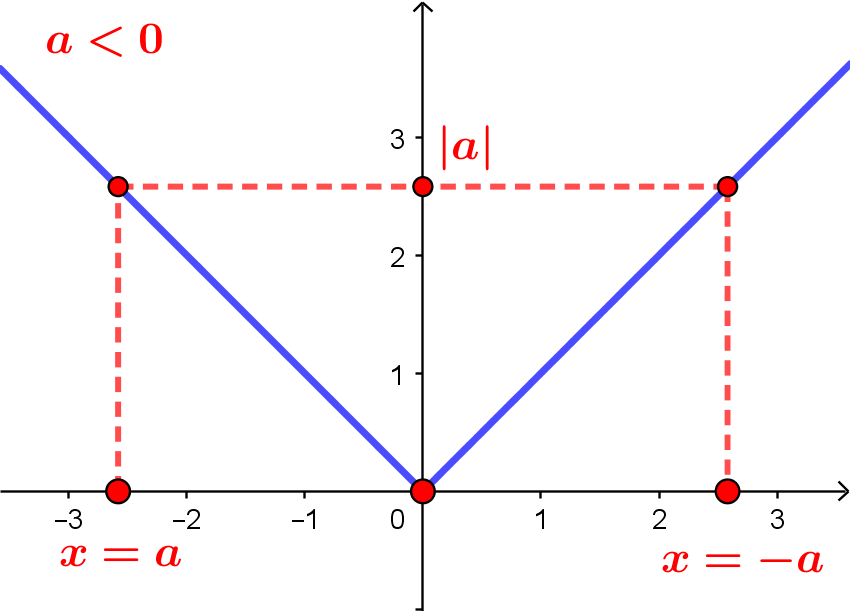
Resolver a equação $|x|=a$, com $a \in \mathbb{R}$.
Primeiro, lembre-se de que $|x| \geqslant 0$ para todo $x \in \mathbb{R}$. Logo, quando $a<0$, não há valores de $x$ tais que $|x| = a$. Isto pode ser confirmado visualmente pelo esboço de gráfico abaixo.
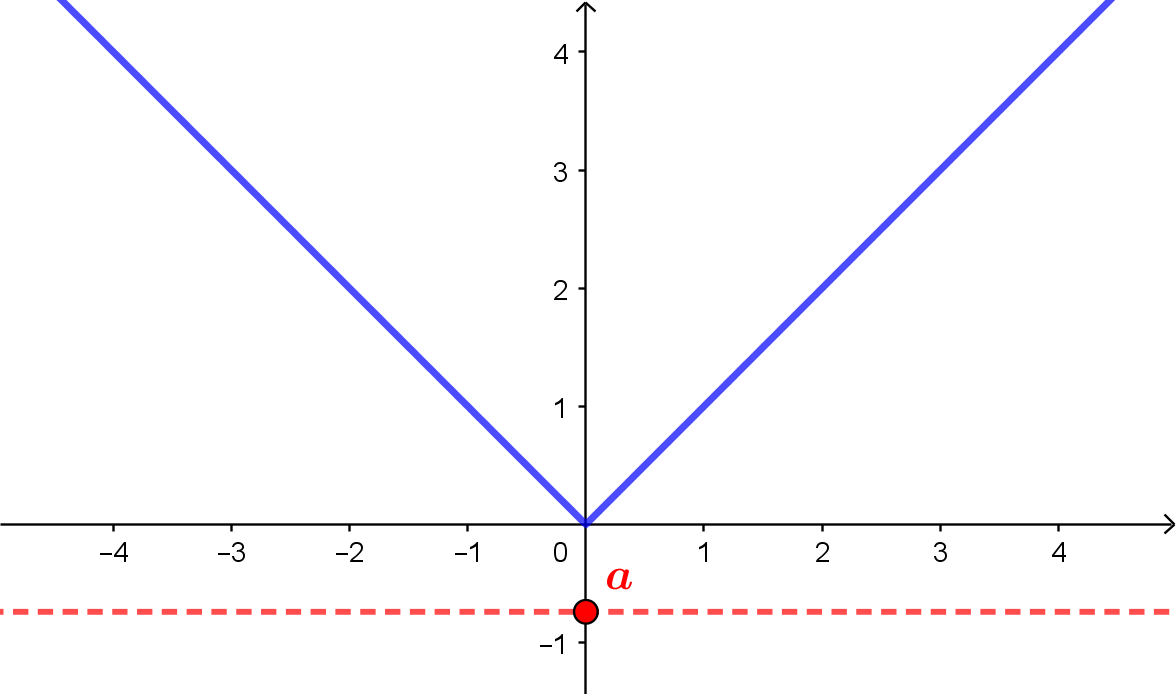
Já quando $a=0$, temos a equação $|x| = 0$, que possui apenas uma solução, $x=0$.
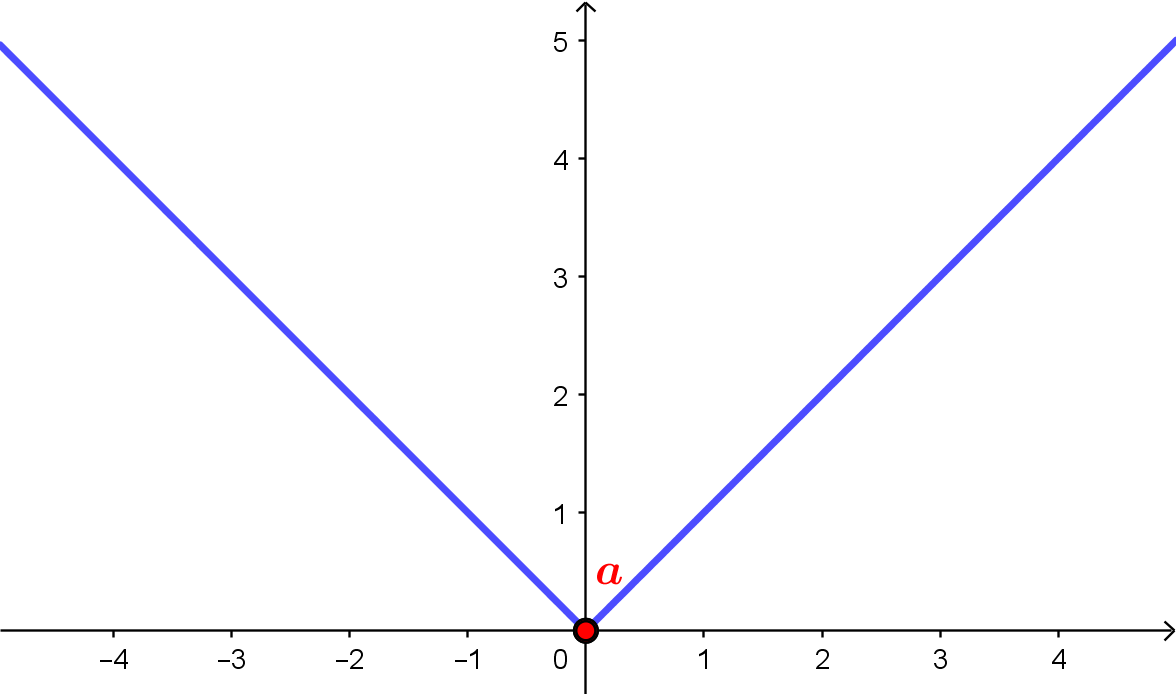
Por fim, observe no gráfico abaixo que, quando $a > 0$, teremos duas soluções, $x=-a$ e $x=a$.
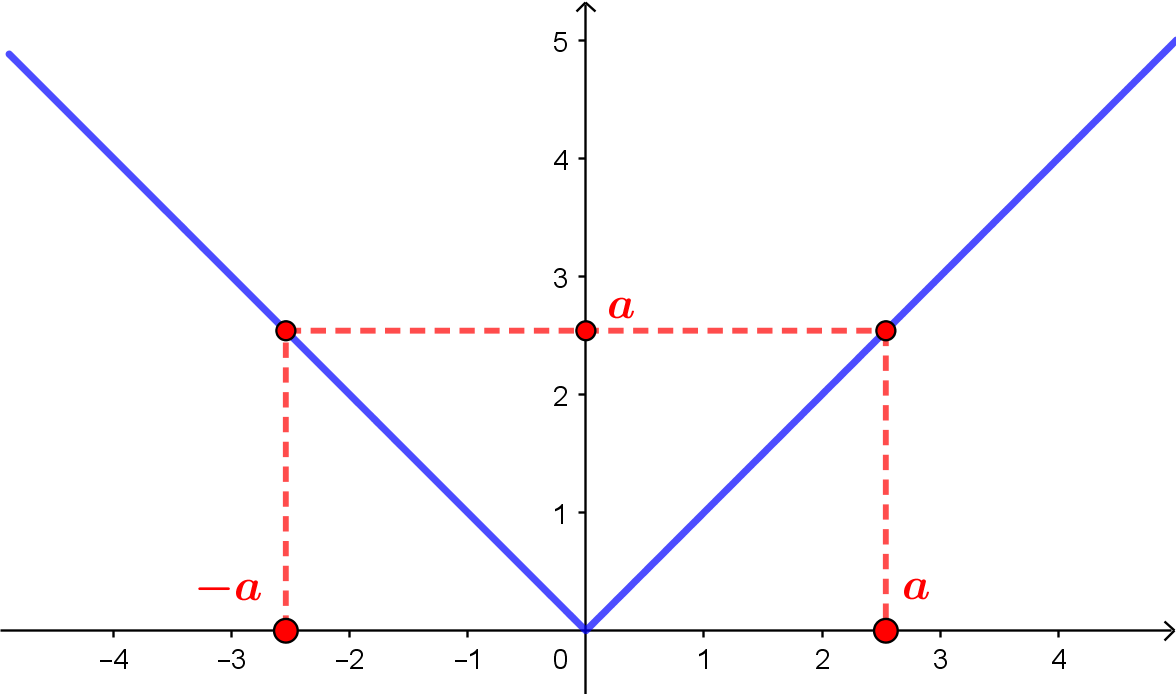
Assim, considerando a equação $|x| = a$,
se $a<0$, sua solução será vazia ($S=\emptyset$) .
se $a=0$, teremos $x=0$ ($S = \{0\}$)
se $a > 0$, teremos $x = a$ ou $x=-a$ ($S = \{-a, a\}$).
Note que podemos unificar a segunda e a terceira possibilidades, escrevendo simplesmente,
se $a<0$, sua solução será vazia ($S=\emptyset$) .
se $a \geqslant 0$, teremos $x = a$ ou $x=-a$ ($S = \{-a, a\}$).
Isto porque se $a=0$, então $-a = a = 0$.
Resolver a equação
\[|2x+1| = 3.\]
Utilizando o que vimos acima, como $3 > 0$,
\begin{eqnarray*} |2x+1| = 3 &\Leftrightarrow& 2x + 1 = 3 \text{ ou } 2x + 1 = -3\\ &\Leftrightarrow& 2x = 3-1 \text{ ou } 2x = -3-1\\ &\Leftrightarrow& 2x = 2 \text{ ou } 2x = -4\\ &\Leftrightarrow& x = 1 \text{ ou } x = -2 \end{eqnarray*}
Resolver a equação
\[|2x+1| = x + 3.\]
Antes de resolver com todo o cuidado, vamos "resolver" de uma forma bastante comum, mas incorreta! (Uma resolução correta será feita após o exemplo seguinte.)
\begin{eqnarray*} |2x+1| = x + 3 &\Leftrightarrow& 2x + 1 = x + 3 \text{ ou } 2x + 1 = -(x+3)\\ \\ &\Leftrightarrow& 2x + 1 = x+3 \text{ ou } 2x + 1 = -x - 3\\ \\ &\Leftrightarrow& 2x - x = 3-1 \text{ ou } 2x + x= -3-1\\ \\ &\Leftrightarrow& x = 2 \text{ ou } 3x = -4\\ \\ &\Leftrightarrow& x = 2 \text{ ou } x = -\frac{4}{3} \end{eqnarray*}
Vamos verificar se está correta esta solução que obtivemos,
\[|2x+1| = x+3 \Leftrightarrow x = 2 \text{ ou } x = -\frac{4}{3}.\]Testando, temos que,
para $x=2$,
\[|2x+1|= |2\cdot 2 + 1| = |5| = 5\]\[x + 3 = 2+3 = 5,\]logo $|2x+1| = x + 3$ quando $x=2$.
para $x=-\frac{4}{3}$,
\[|2x+1|=\left|2\cdot \left(-\frac{4}{3}\right) + 1\right| = |-\frac{8}{3} + 1| = |-\frac{5}{3}| = \frac{5}{3}\]
\[x+3 = -\frac{4}{3} + 3 = \frac{-4+9}{3} = \frac{5}{3},\]logo $|2x+1| = x + 3$ quando $x=-\frac{4}{3}$.
Então $x=2$ e $x=-\frac{4}{3}$ são mesmo solução da equação.
Porém, a forma como resolvemos está incorreta, mesmo que tenha conduzido, neste caso à solução correta. Esquecemos de algo muito importante nesta "solução"! Você saberia dizer o quê?
Antes de entendermos o que fizemos errado e resolver corretamente, vamos a um outro exemplo.
Resolver a equação
\[|2x-1| = 3x + 2.\]
Vamos "resolver" como fizemos no exemplo anterior... incorretamente!
\begin{eqnarray*} |2x-1| = 3x+2 &\Leftrightarrow& 2x - 1 = 3x + 2 \text{ ou } 2x - 1 = -(3x+2)\\ \\ &\Leftrightarrow& 2x - 1 = 3x+2 \text{ ou } 2x - 1 = -3x - 2\\ \\ &\Leftrightarrow& 2x - 3x = 2+1 \text{ ou } 2x + 3x= -2+1\\ \\ &\Leftrightarrow& -x =3 \text{ ou } 5x = -1\\ \\ &\Leftrightarrow& x = -3 \text{ ou } x = -\frac{1}{5} \end{eqnarray*}Obtivemos
\[|2x-1| = 3x+2 \Leftrightarrow x = -3 \text{ ou } x = -\frac{1}{5}\]Verificando, temos que,
para $x=-3$,
\[|2x-1|= |2\cdot (-3) - 1| = |-7| = 7\]\[3x + 2 = -3(-3) + 2 = -7, {\color{red} \text{ ou seja, não vale que } |2x-1| = 3x+2}\];
para $x=-\frac{1}{5}$,
\[|2x-1|= \left|2\cdot \left(-\frac{1}{5}\right) - 1\right| = \left|-\frac{7}{5}\right| = \frac{7}{5}\]
\[3x + 2 = -\frac{3}{5}+2 = \frac{7}{5}\]. Portanto, $x=-\frac{1}{5}$ é uma solução.
Assim, nossa técnica de solução está incorreta, pois gerou pelo menos uma raiz "falsa"!
O que fizemos de errado na solução dos exemplos anteriores?
Nos exemplos 7 e 8, utilizamos que
\[|2x-1| = 3x+2 \Leftrightarrow 2x - 1 = 3x + 2 \text{ ou } 2x - 1 = -(3x+2),\]
ou seja, tentamos resolver como no caso $|x|=a$, que, apenas quando $\boldsymbol{a\geqslant 0}$, equivale a
$x=a \text{ ou } x=-a$. Acontece que não podemos garantir, em princípio, que $x + 3 \geqslant 0$ e $3x+2 \geqslant 0$.
Voltando à solução da equação $|x| = a$,
Se $a<0$, a solução é vazia ($S=\emptyset$) .
Se $a=0$, temos $x=0$ ($S = \{0\}$)
Se $a > 0$, temos $x = a$ ou $x=-a$ ($S = \{-a, a\}$).
Podemos então escrever, de maneira geral, que
\[|x| = a \Leftrightarrow (x = a \;\text{ ou }\; x = -a) \;\text{ e }\; a\geqslant 0,\] isto é, $|x|=a$ é equivalente a $x=a$ ou $x=-a$ se, simultaneamente, tivermos $a \geqslant 0$.
Vamos voltar aos exemplos e resolvê-los corretamente:
Resolver a equação
\[|2x+1| = x + 3.\]
Temos
\begin{eqnarray*} |2x+1| = x+ 3 &\Leftrightarrow& \left(2x + 1 = x + 3 \text{ ou } 2x + 1 = -(x+3) \right)\text{ e } x+3 \geqslant 0\\ \\ &\Leftrightarrow& \left(2x + 1 = x+3 \text{ ou } 2x + 1 = -x - 3\right) \text{ e } x \geqslant -3\\ \\ &\Leftrightarrow& \left(2x - x = 3-1 \text{ ou } 2x + x= -3-1\right) \text{ e } x \geqslant -3\\ \\ &\Leftrightarrow& \left(x = 2 \text{ ou } 3x = -4\right) \text{ e } x \geqslant -3\\ \\ &\Leftrightarrow& \left(x = 2 \text{ ou } x = -\frac{4}{3}\right) \text{ e } x \geqslant -3\\ \\ &\Leftrightarrow& x = 2 \text{ ou } x = -\frac{4}{3} \end{eqnarray*}
Resolver a equação
\[|2x-1| = 3x + 2.\]
Temos
\begin{eqnarray*} |2x-1| = 3x+2 &\Leftrightarrow& \left(2x - 1 = 3x + 2 \text{ ou } 2x - 1 = -(3x+2)\right) \text{ e } 3x + 2 \geqslant 0 \\ \\ &\Leftrightarrow& \left(2x - 1 = 3x+2 \text{ ou } 2x - 1 = -3x - 2\right) \text{ e } 3x \geqslant -2 \\ \\ &\Leftrightarrow& \left(2x - 3x = 2+1 \text{ ou } 2x + 3x= -2+1\right) \text{ e } x \geqslant -\frac{2}{3}\\ \\ &\Leftrightarrow& \left(-x =3 \text{ ou } 5x = -1\right) \text{ e } x \geqslant -\frac{2}{3}\\ \\ &\Leftrightarrow& \left(x = -3 \text{ ou } x = -\frac{1}{5}\right) \text{ e } x \geqslant -\frac{2}{3}\\ \\ &\Leftrightarrow& x = -\frac{1}{5}. \end{eqnarray*}Na última equivalência, descartamos $x=-3$ pois não satisfaz a condição $x \geqslant -\frac{2}{3}$.
Resolver a equação
\[|x| = |a|.\]
Note que dois números reais $x$ e $a$ terão o mesmo módulo se, e somente se, $x=a$ ou $x=-a$.
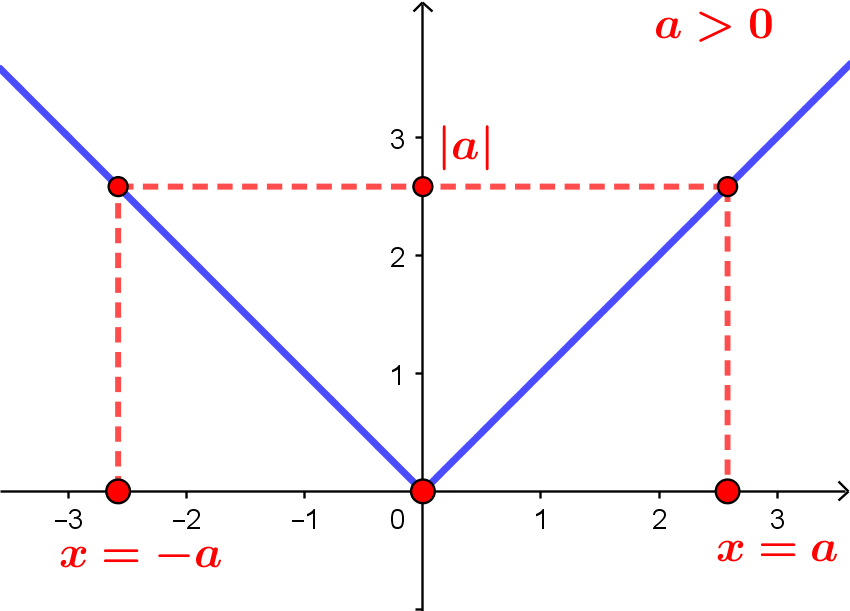
Assim,
\[|x|=|a| \Leftrightarrow x = a \;\text{ ou }\; x = -a.\]
Resolver a equação
\[|x+3| = |2x-1|\]
Utilizando a equivalência
\[|x|=|a| \Leftrightarrow x = a \;\text{ ou }\; x = -a\]vista no exemplo anterior, temos
\begin{eqnarray*} |x+3| = |2x-1| &\Leftrightarrow& x+3 = 2x-1 \;\text{ ou }\; x+3 = -(2x-1)\\ \\ &\Leftrightarrow& x+3 = 2x-1 \;\text{ ou }\; x+3 = -2x+1\\ \\ &\Leftrightarrow& x-2x = -1-3 \;\text{ ou }\; x+2x = 1-3\\ \\ &\Leftrightarrow& -x = -4 \;\text{ ou }\; 3x = -2\\ \\ &\Leftrightarrow& x = 4 \;\text{ ou }\; x = -\frac{2}{3} \end{eqnarray*}
Resolver a inequação
\[|x| > a.\]
Primeiramente, vamos pensar no caso em que $a > 0$. Observando o gráfico
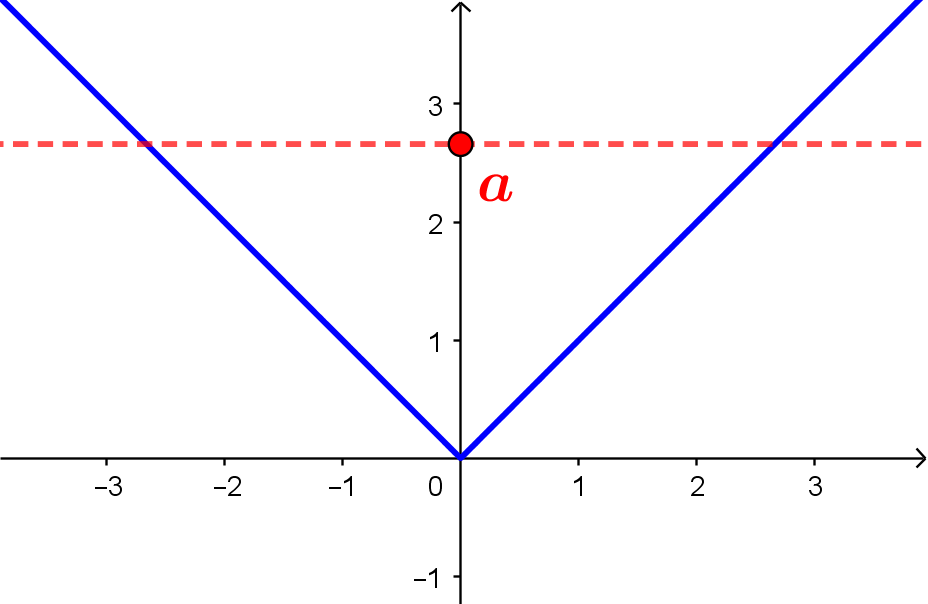
podemos ver que $|x| > a$ apenas quando $x > a$ ou $x < -a$.
Se $a < 0$, então $|x| > a$ será sempre verdadeiro, pois, para todo $x \in \mathbb{R}$, $|x| \geqslant 0 > a$. E também sempre será verdade que $x > a$ ou $x < -a$, pois teremos $a< 0 \leqslant x$ ou $-a > 0 \geqslant x$.
Se $a = 0$, então $|x| > a$ se, e somente se, $x \neq 0$, caso nos quais também teremos $x > a = 0$ ou $x < -a = 0$.
Assim, para todo $x \in \mathbb{R}$, vale a equivalência abaixo:
Resolver a inequação
\[|x| \geqslant a.\]
Como no exemplo anterior,
\[|x| \geqslant a \Leftrightarrow x \geqslant a \;\text{ ou } x \leqslant -a\]
Resolver a inequação
\[|2x + 5| > 3\]
Utilizando a equivalência vista no exemplo anterior, temos
\begin{eqnarray*} |2x + 5| > 3 &\Leftrightarrow& 2x + 5 > 3 \;\text{ ou }\; 2x + 5 < -3\\ \\ &\Leftrightarrow& 2x > 3 - 5 \;\text{ ou }\; 2x < -3 - 5\\ \\ &\Leftrightarrow& 2x > -2 \;\text{ ou }\; 2x < -8\\ \\ &\Leftrightarrow& x > -1 \;\text{ ou }\; x < -4 \end{eqnarray*}
Resolver a inequação
\[|x|<a.\]
Pensando no caso em que $a> 0$, observando o gráfico da função modular,  vemos que
vemos que
Se $a\leqslant0$, é fácil ver que $|x| < a$ nunca é verdadeiro. Por outro lado, como $a<0$, não poderemos ter, simultaneamente, $x < a$ e que $x > -a$.
Assim, para todo $x \in \mathbb{R}$, temos a equivalência
Note ainda que
\[|x| \leqslant a \Leftrightarrow -a \leqslant x \leqslant a \Leftrightarrow (x \geqslant -a) \;\text{ e }\; (x \leqslant a)\]
Resolver a inequação
\[|5 - 2x| \leqslant 3\]
Pela equivalência do exemplo anterior, temos
\begin{eqnarray*} |5 - 2x| > 3 &\Leftrightarrow& 5 - 2x \geqslant -3 \;\text{ e }\; 5 - 2x \leqslant 3\\ \\ &\Leftrightarrow& - 2x \geqslant -3 - 5\;\text{ e }\; - 2x \leqslant 3 - 5\\ \\ &\Leftrightarrow& - 2x \geqslant -8\;\text{ e }\; - 2x \leqslant -2\\ \\ &\Leftrightarrow& x \leqslant 4\;\text{ e }\; x \geqslant 1\\ \\ &\Leftrightarrow& 1 \leqslant x \leqslant 4 \end{eqnarray*}
Resolver a inequação
\[|x + 3| < |2x-1|\]
Vamos ler a inequação com $p = x+3$ e $a = |2x-1|$:
\[\begin{array}{rcl} \overbrace{\hphantom{|x + 3|}}^{|p|}& &\overbrace{\hphantom{|2x -1|}}^{a}\\ |x + 3| &<& |2x-1| \end{array}\]Podemos então usar a equivalência vista no exemplo 16:
\[ \begin{array}{rclcccc} \overbrace{\hphantom{|x + 3|}}^{|p|}& &\overbrace{\hphantom{|2x -1|}}^{a} & & \overbrace{\hphantom{\left(x + 3 > -|2x-1|\right)}}^{(p > -a)} && \overbrace{\hphantom{\left(x + 3 < |2x-1|\right)}}^{(p < a)}\\ \\ |x + 3| &<& |2x-1| &\Leftrightarrow& \left(x + 3 > -|2x-1|\right) &\text{ e }& \left(x + 3 < |2x-1|\right) \end{array}\]Reorganizando as desigualdades do lado direito, temos
\[|x + 3| < |2x-1| \Leftrightarrow \left(|2x-1| > -x - 3\right) \text{ e } \left(|2x-1| > x + 3\right)\]Vamos analisar as duas desigualdades que aparecem do lado direito. A desigualdade $|2x-1| > -x - 3$ é da forma $|p| > a$, portanto temos
\[ |2x-1| > -x - 3 \Leftrightarrow 2x-1 > -x - 3 \;\text{ ou }\; 2x-1 < -(-x - 3).\]O mesmo vale para a desigualdade $|2x-1| > x + 3$, e podemos reescrever
\[|2x-1| > x + 3\Leftrightarrow 2x-1 > x + 3 \;\text{ ou }\;2x-1 < -(x + 3).\]Assim,
\[ \begin{array}{ccccccccc} \\ \end{array} \]\[ \begin{array} {ccccccccc} |x + 3| < |2x-1 & \Leftrightarrow & (2x-1 > -x - 3) & \text{ ou } & 2x-1 <-(-x - 3)) & \text{ e } & (2x-1 > x + 3 & ou & 2x-1 < -(x + 3)) \\ \\ & \Leftrightarrow & \left(2x-1 > -x - 3 \right.&\text{ ou }&\left. 2x-1 < x + 3\right) & e & \left(2x-1 > x + 3\right. &\text{ ou }& \left.2x-1 < -x - 3\right) \\ \\ & \Leftrightarrow & \left(3x > -2 \right.&\text{ ou }&\left. x < 4\right) &\text{ e }& \left(x > 4\right. &\text{ ou }& \left.3x < -2\right) \\ \\ & \Leftrightarrow & & \underbrace{\left(x > -\frac{2}{3} \right. \text{ ou } \left. x < 4\right)} & &\text{ e }& \left(x > 4\right. &\text{ ou }& \left.x < -\frac{2}{3}\right) \\ \\ & \Leftrightarrow & & {(x \in \mathbb{R})} & &\text{ e }& \left(x > 4\right. &\text{ ou }& \left.x < -\frac{2}{3}\right) \\ \\ & \Leftrightarrow& {x > 4 \; \text{ ou } \; x < -\frac{2}{3} } \\ \\ \end{array} \]
Observe que é sempre verdade a condição $\left(x > -\frac{2}{3} \text{ ou } x < 4\right)$; qualquer número real $x$ satisfaz pelo menos uma das duas desigualdades.
Voltando a falar do módulo de números reais
Vamos acrescentar às propriedades 1 outras que surgiram do estudo das inequações, que fizemos na seção anterior.
O módulo possui as seguintes propriedades
- $|x| \geqslant 0, \forall x \in \mathbb{R}$. Além disso, $|x| = 0 \Leftrightarrow x = 0$.
- $|-x|=|x|, \forall x \in \mathbb{R}$.
- $|x| = a \Leftrightarrow (x = a \;\text{ ou }\; x = -a) \;\text{ e }\; a\geqslant 0$.
- $|x| = |a| \Leftrightarrow x=a \text{ ou } x = -a$.
- $|x| > a \Leftrightarrow x > a \;\text{ ou } x < -a$
- $|x| \geqslant a \Leftrightarrow x \geqslant a \;\text{ ou } x \leqslant -a$
- $|x| < a \Leftrightarrow -a < x < a \Leftrightarrow (x > -a) \;\text{ e }\; (x < a)$
- $|x| \leqslant a \Leftrightarrow -a \leqslant x \leqslant a \Leftrightarrow (x \geqslant -a) \;\text{ e }\; (x \leqslant a)$
O módulo possui uma importante interpretação geométrica. Observe os pontos abaixo, marcados sobre a reta dos números reais:
Representando por $d(A,B)$ a distância entre os pontos $A$ e $B$, temos
De maneira geral, considerando $a, b \in \mathbb{R}$, a distância $d(a,b)$ entre $a$ e $b$ será dada por
\[d(a, b) = \begin{cases} b - a, & \text{se } b \geqslant a\\a - b, & \text{se } a > b \end{cases} = |b-a|.\]Conclusão: $|b - a|$ representa a distância entre os números $a$ e $b$ na reta numérica.
Resolver geometricamente a desigualdade $|x + 1| < |x - 2|$.
Temos que
$|x + 1| = |x - (-1)|$ é a distância de $x$ a $-1$.
$|x - 2|$ é a distância de $x$ a $2$.
Assim, para que $|x - (-1)| < |x - 2|$, a distância de $x$ a $-1$ deve ser menor do que a distância de $x$ a $2$. Abaixo esboçamos o conjunto dos pontos que satisfazem a esta condição.

O conjunto solução é dado então por $S = \left(-\infty, \frac{1}{2}\right).$
O que representa o conjunto dos valores de $x\in\mathbb{R}$ tais que $|x-2| < 3$?
Note que $|x-2| < 3 \Leftrightarrow d(x,2) < 3.$
Assim, geometricamente, a desigualdade é satisfeita pelos valores de $x \in \mathbb{R}$ cuja distância ao 2 é menor do que 3,

ou seja, o intervalo $(-1, 5)$.
O que representa o conjunto dos valores de $x\in\mathbb{R}$ tais que $|x-c| < r$?
Note que $|x-c| < r \Leftrightarrow d(x,c) < r.$
Assim, geometricamente, a desigualdade é satisfeita pelos valores de $x \in \mathbb{R}$ cuja distância a $c$ é menor do que $r$,

ou seja, o intervalo $(c-r, c+r)$.

