Transformações de Gráficos de Funções
Dependendo da composição de funções que consideremos, poderemos facilmente identificar o gráfico do resultado da composição das funções observando o gráfico de uma das funções da composição. Nesta seção, considerando uma constante $c>0$, vamos apresentar como obter, a partir do gráfico da função $y=f(x)$, os gráficos das funções:
|
|
Veremos adiante como obter estas e outras transformações de gráficos de funções.
No applet abaixo, temos o exemplo de uma função dada por um polinônio de grau 3. Clicando nas diversas opções em escolhendo o valor para a constante $c$, você poderá experimentar como cada um dos tipos de composição transforma o gráfico. Antes de escolher as opções, você também pode também tentar adivinhar qual será o esboço do gráfico. Você também pode desmarcar a opção de mostrar $f(x)$, para poder visualizar melhor o gráfico obtido em qualquer uma das outras transformações.
Translações
Para obter o gráfico da função
$y=f(x)+c$, devemos deslocar o gráfico de $y=f(x)$ em $c$ unidades para cima;
$y=f(x)-c$, devemos deslocar o gráfico de $y=f(x)$ em $c$ unidades para baixo.
Para obter o gráfico da função $y=\cos( x) + \frac{3}{2}$ devemos deslocar $\frac{3}{2}$ unidades para cima, o gráfico da função $y= \cos (x)$.
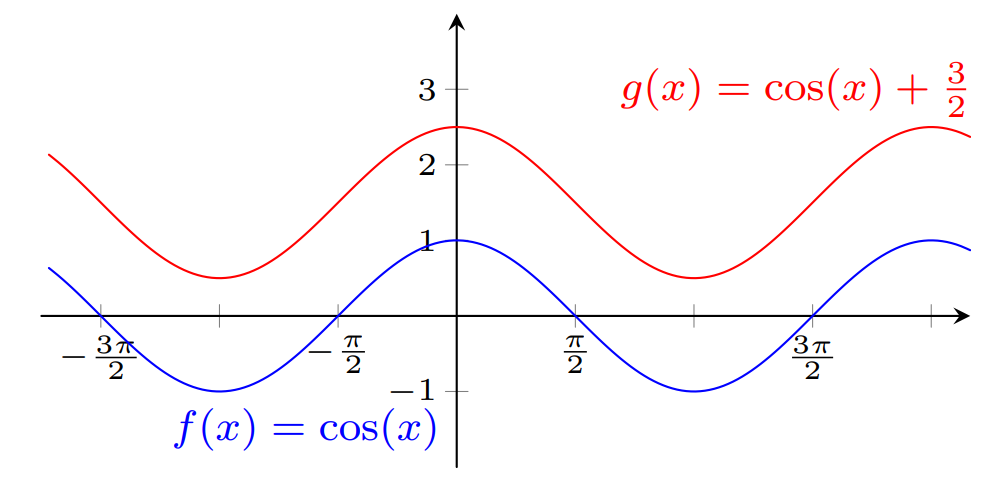
Pode ver uma animação em Geogebra que ilustra esta transformação, no endereço abaixo:
Para obter o gráfico de:
$y=f(x-c)$, desloque o gráfico de $y=f(x)$ em $c$ unidades para a direita;
$y=f(x+c)$, desloque o gráfico de $y=f(x)$ em $c$ unidades para a esquerda.
Para obter o gráfico da função $y=\left(x - \frac{5}{2}\right)^2$ devemos deslocar $\frac{5}{2}$ unidades para a direita, o gráfico da função $y= x^2$.
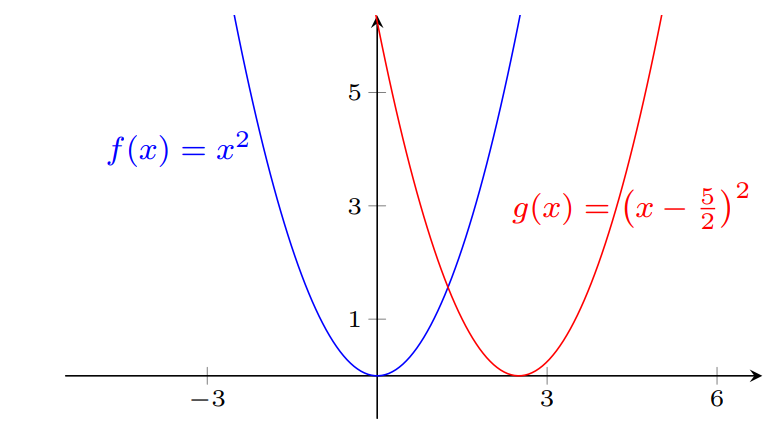
No endereço abaixo poderá ver uma animação com a translação horizontal do gráfico da função $f(x)= x^2$:
Expansão e Compressão
Suponha que $c>1$. Para obter o gráfico de:
$y=cf(x)$, expanda o gráfico de $y=f(x)$ verticalmente por um fator de $c$
$y=(1/c)f(x)$, comprima o gráfico de $y=f(x)$ verticalmente por um fator de $c$
Para obter o gráfico da função $y=2\cos (x)$ devemos expandir verticalmente o gráfico da função $y= \cos (x)$ pelo fator $2$.
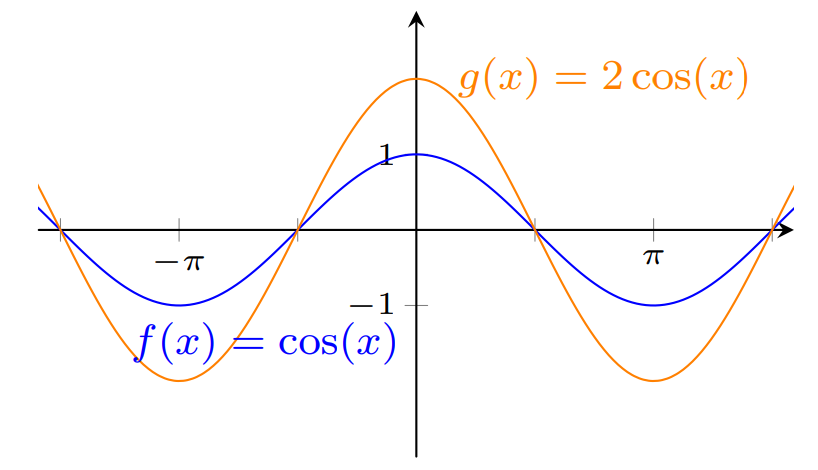
Para obter o gráfico da função $y=\frac{1}{2}\cos (x)$ devemos comprimir verticalmente o gráfico da função $y= \cos (x)$ pelo fator $2$.
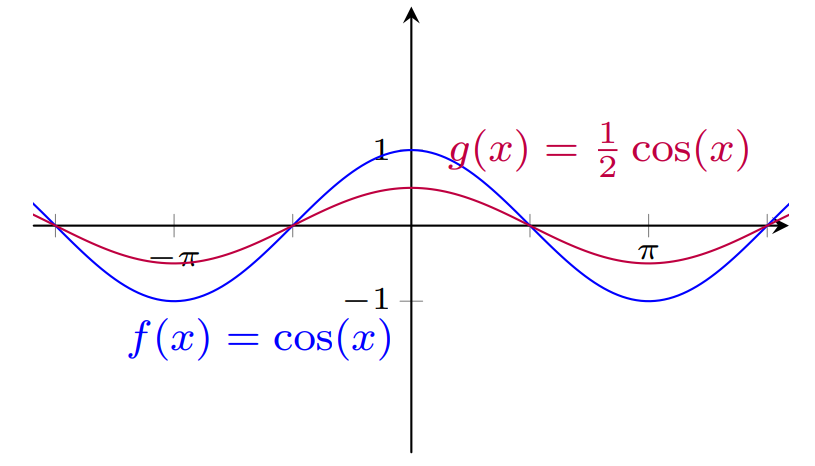
Suponha que $c>1$. Para obter o gráfico de:
$y=f(cx)$, comprima o gráfico de $y=f(x)$ horizontalmente por um fator de $c$;
$y=f(x/c)$, expanda o gráfico de $y=f(x)$ horizontalmente por um fator de $c$.
Para obter o gráfico da função $y=\cos (3x)$ devemos comprimir horizontalmente o gráfico da função $y= \cos (x)$ pelo fator $3$.
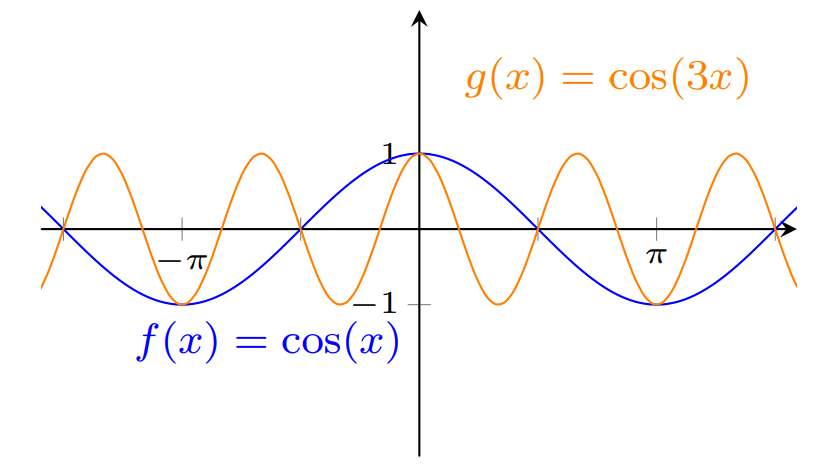
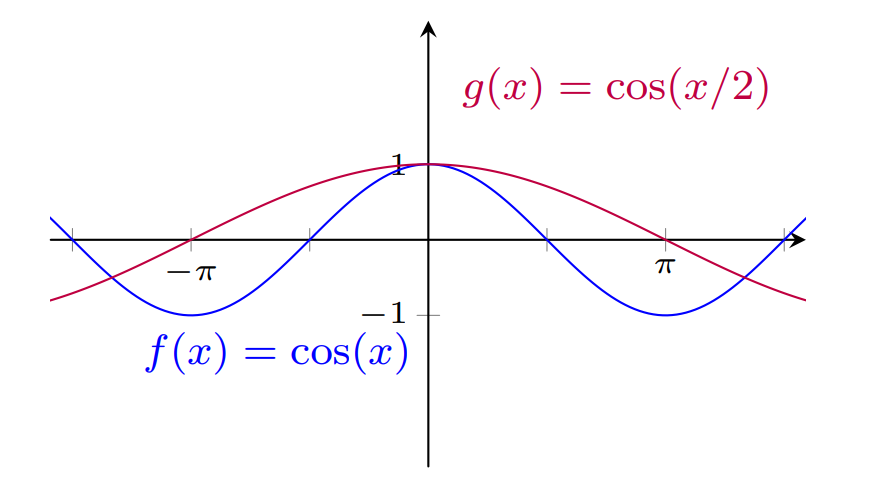
Para obter o gráfico da função $y=\cos (x/2)$ devemos expandir horizontalmente o gráfico da função $y= \cos (x)$ pelo fator $2$.
Reflexão
Para obter o gráfico de:
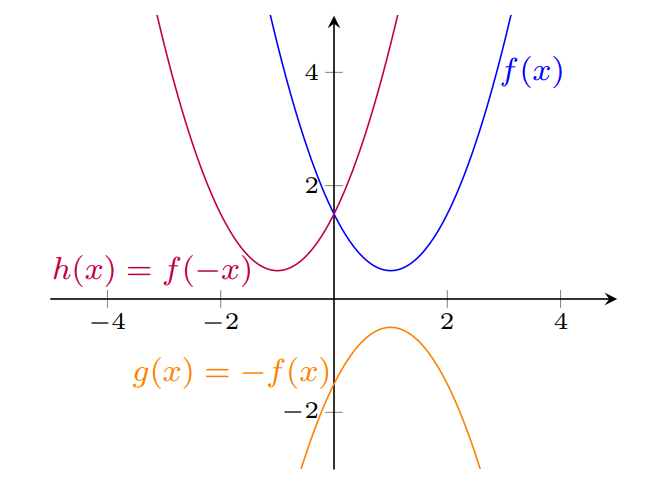
$y=-f(x)$, reflita o gráfico de $y=f(x)$ em torno do eixo $x$.
$y=f(-x)$, reflita o gráfico de $y=f(x)$ em torno do eixo $y$.
Reflexões do gráfico de $f(x)=1/2 + (x-1)^2$ em torno do eixo $x$ e do eixo $y$.
Vejamos como podemos obter o gráfico da função $f(x)=2\sqrt{x+4}-1$ a partir do gráfico de $y=\sqrt{x}$.
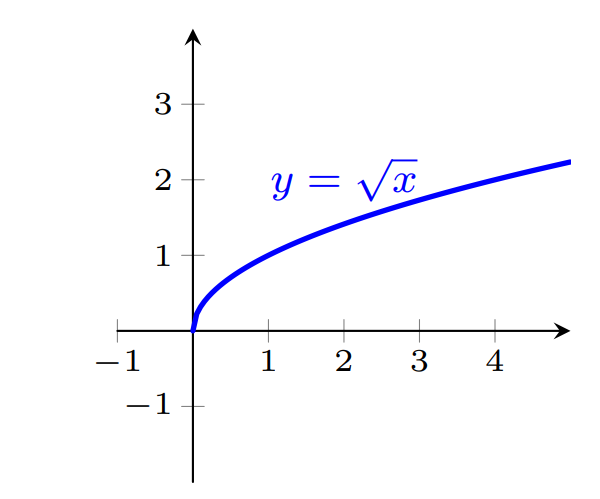
Transladando o gráfico anterior 4 unidades para a esquerda, obtemos o gráfico abaixo da função $y=\sqrt{x+4}$.
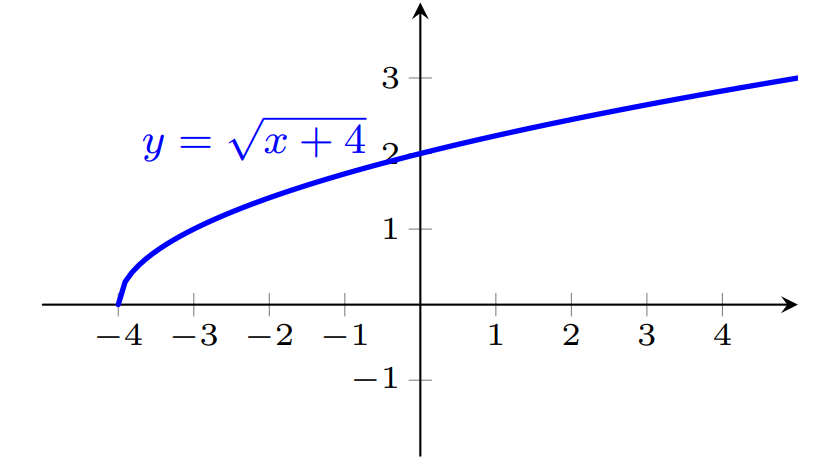
Depois multiplicamos por 2 a expressão da função anterior, fazemos com que o gráfico expanda na direção vertical por um fator 2, conforme a figura abaixo.
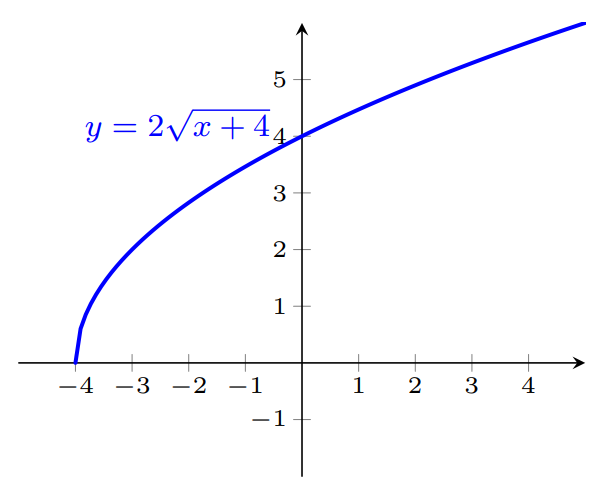
E para obter o gráfico da função pedida, basta transladar na vertical o gráfico anterior em uma unidade para baixo.
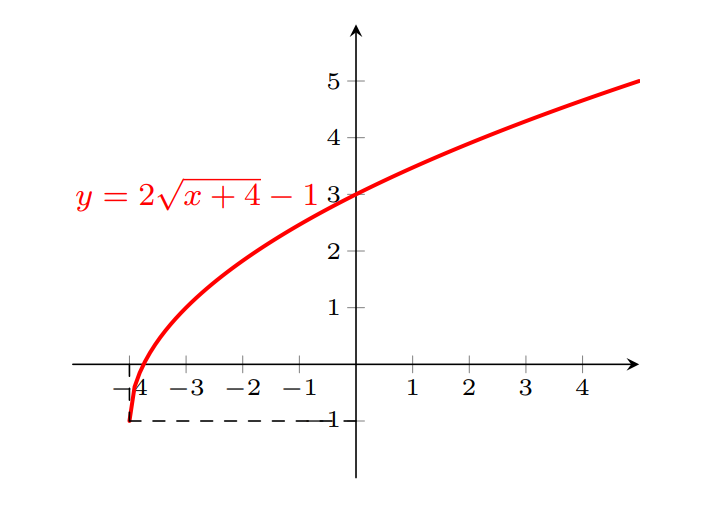
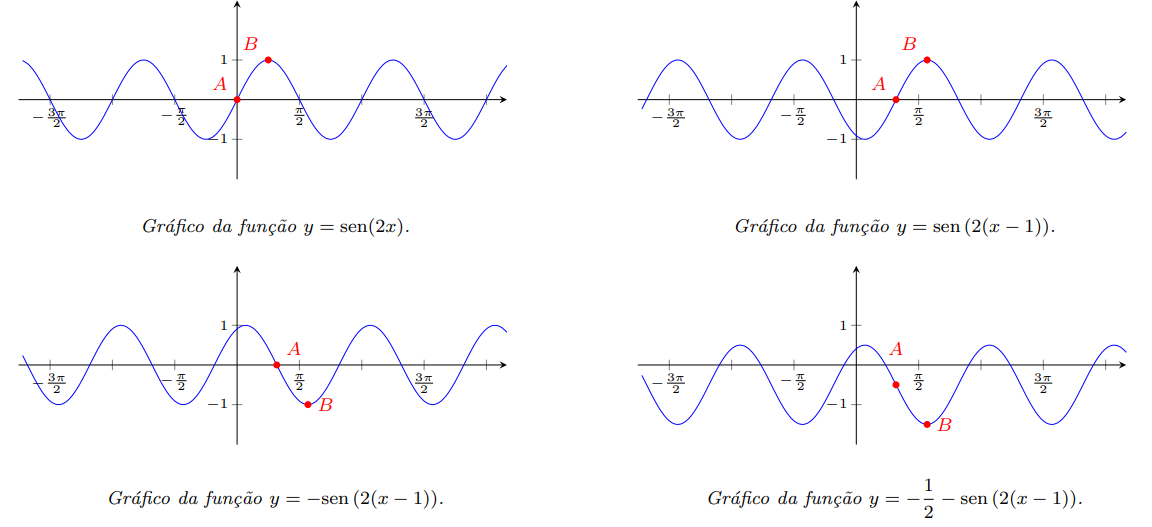
Para obter o gráfico da função $f(x)=-1/2-\textrm{sen}(2(x-1))$, podemos aplicar transformações ao gráfico de $f(x) = \textrm{sen} (x)$.
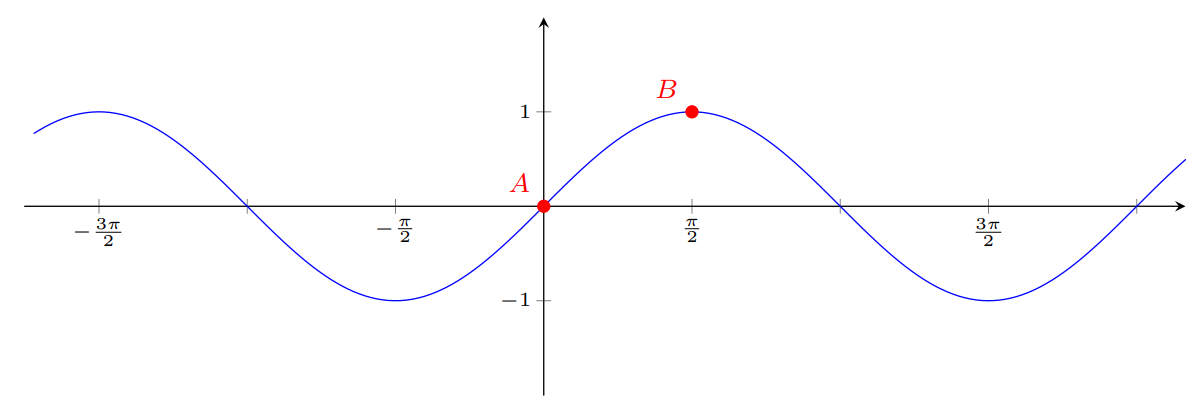
Os pontos $A$ e $B$ forma marcados no gráfico para irmos acompanhando o movimento deles, à medida que fazemos as transformações do gráfico.
Módulos
Outras transformações de gráficos que também são interessantes, são as que envolvem o valor absoluto.
Se $y=|f(x)|$, então por definição de valor absoluto temos:
$$|f(x)|= \left\{\begin{array}{lcc}f(x), & \text{se} & f(x) \geq 0. \\-f(x), & \text{se} & f(x) < 0.\end{array}\right.$$Assim, vemos que podemos obter o gráfico de $y=|f(x)|$ a partir do gráfico de $y=f(x)$. O gráfico de $y=|f(x)|$ coincide
com o gráfico de $y=f(x)$ nos pontos $(x,y)$ tais que $y=f(x) \geq 0$;
com o gráfico de $y=-f(x)$ nos pontos $(x,y)$ tais que $y=f(x) < 0$.
Para obter o gráfico de $\displaystyle g(x)=\left|\frac{1}{2} - (x-1)^2\right|$, podemos partir do gráfico de $\displaystyle f(x)=\frac{1}{2} - (x-1)^2$ e usar a descrição acima.
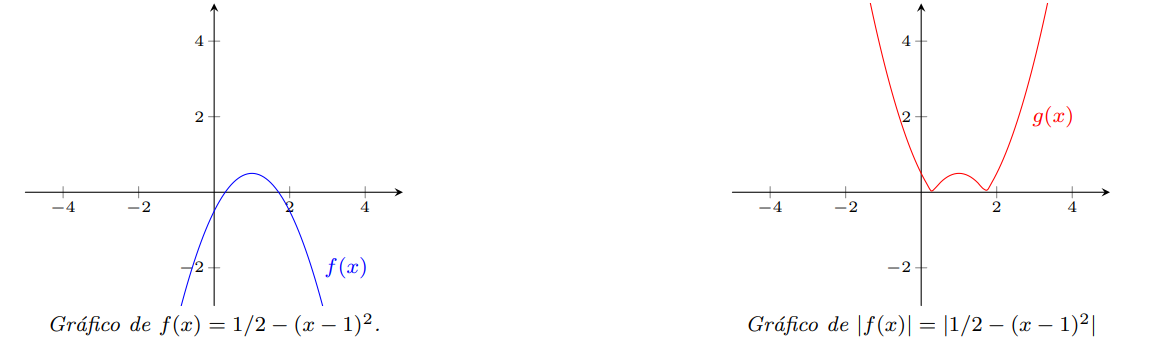
Vejamos agora como obter o gráfico da função $y=f(|x|)$ a partir do gráfico de $y=f(x)$. Por definição de valor absoluto, temos:
$$f(|x|)= \left\{\begin{array}{lcc}f(x), & \text{se} & x \geq 0. \\f(-x), & \text{se} & x < 0.\end{array}\right.$$Note que o domínio de $f$, deve conter valores positivos ou $0$, isto é $\mathrm{D}(f) \cap[0,+\infty) \neq \emptyset$ para que a função $f(|x|)$ esteja definida. Além disso, o domínio de $y=f(|x|)$ será um conjunto simétrico relativamente a $x=0$, pois será formado por todos os valores reais de $x$, tais que $|x|\in \mathrm{D}(f)$.
Logo:
o gráfico de $y=f(|x|)$ nos pontos $(x,y)$ tais que $x \geq 0$, coincide com o gráfico de $y=f(x)$.
nos pontos $(x,y)$ onde $x<0$, o gráfico de $y=f(|x|)$ é o simétrico do gráfico de $y=f(x)$ em relação ao eixo $y$.
Consideremos o gráfico de $f(x)=\sqrt{x}$, com $x \in [0,+\infty)$
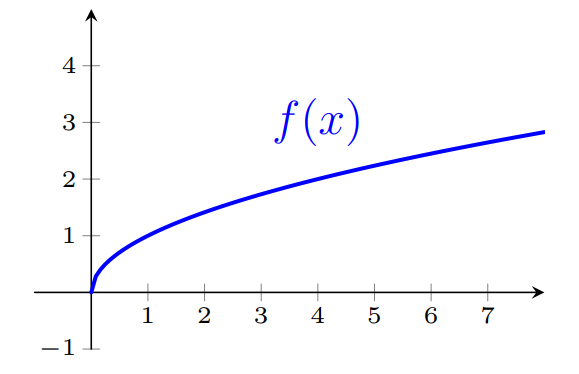
Para obter o gráfico da função $g(x)=f(|x|)$, devemos "espelhar" o gráfico de $f$ ao longo do eixo $y$, obtendo então
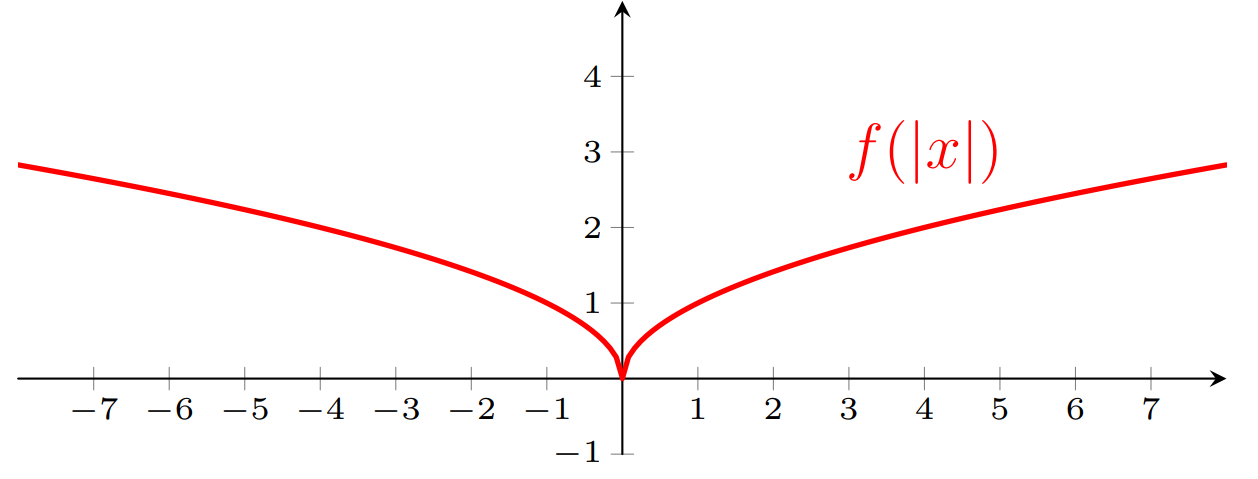
Note que o domínio da função $g$ é $\mathrm{D}(g)=\mathbb{R}$.
Para obter o gráfico de $g(x)=-1+(|x|-2)^2$, podemos partir do gráfico de $f(x)=-1+(x-2)^2$ e usar a descrição acima.
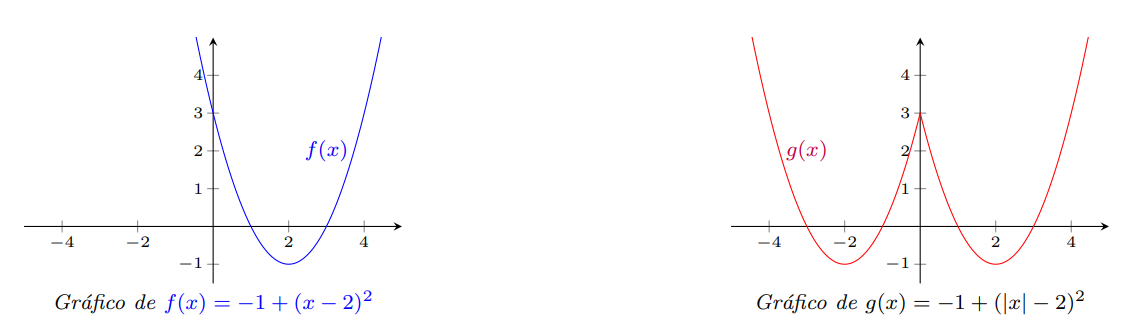
Vejamos como obter o gráfico da função $\displaystyle f(x)=2+\frac{1}{|x|-3}$.
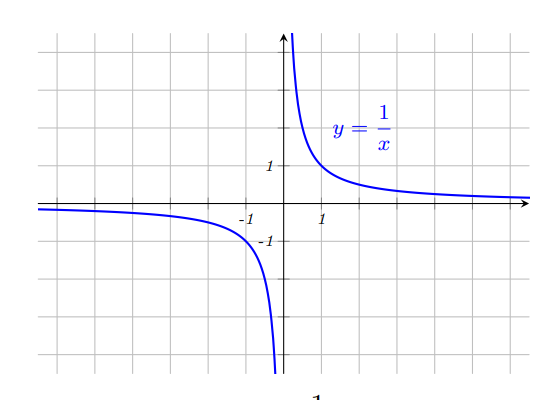
Podemos suspeitar que conseguiremos obter esse gráfico, aplicando transformações ao gráfico de $g(x) = \dfrac{1}{x}$.
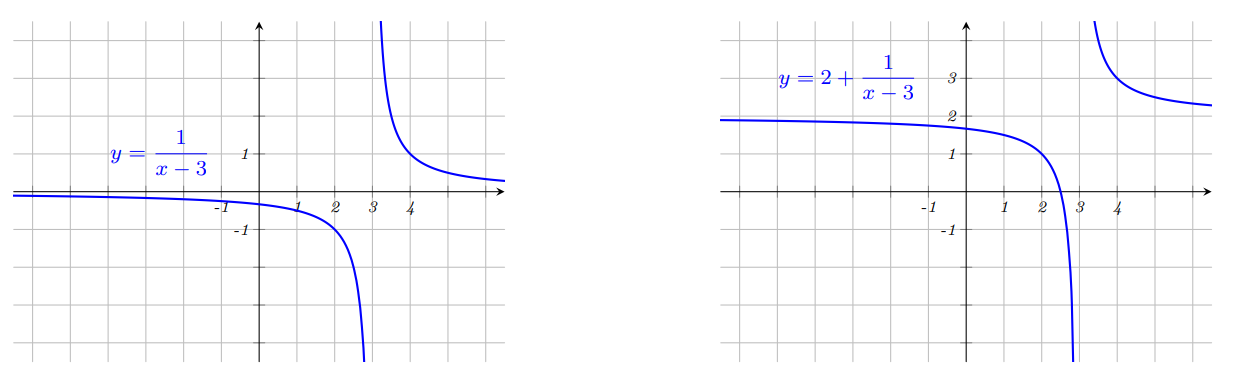
O primeiro passo é transladar o gráfico de $\displaystyle y=\frac{1}{x}$, 3 unidades para a direita de forma a obter o gráfico abaixo à esquerda e depois transladar este último 2 unidades para cima, obtendo o gráfico abaixo à direita.
Para passarmos do gráfico $\displaystyle y=2+\frac{1}{x-3}$ para o gráfico de $\displaystyle y=2+\frac{1}{|x|-3}$, devemos manter a parte do gráfico que corresponde aos pontos $(x,y)$ com $x \geq 0$ e fazer uma reflexão desta parte do gráfico em relação ao eixo $y$. Obtendo portanto o gráfico abaixo, que corresponde ao nosso objetivo.
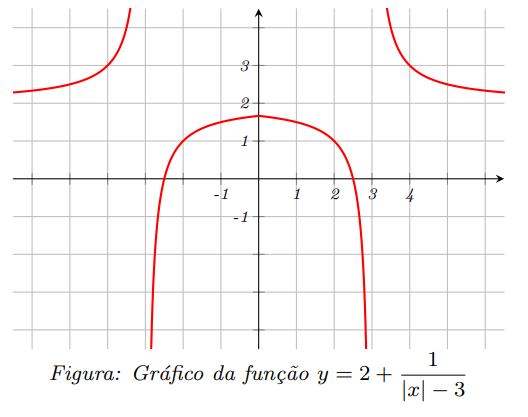
Observe que o gráfico da função obtida tem duas assíntotas verticais em $x=-3$ e $x=3$ e uma assíntota horizontal em $y=1$.

