A ideia de Limite

Nesta seção, vamos introduzir o conceito de limite de forma intuitiva, a partir da análise de gráficos de funções. Estudaremos os limites laterais (à esquerda e à direita) em pontos determinados. Antes de prosseguir, assista ao vídeo abaixo:

Vídeo "Introdução à Noção de Limites"

Agora, prossiga com o estudo dos exemplos abaixo.

Exemplo 1

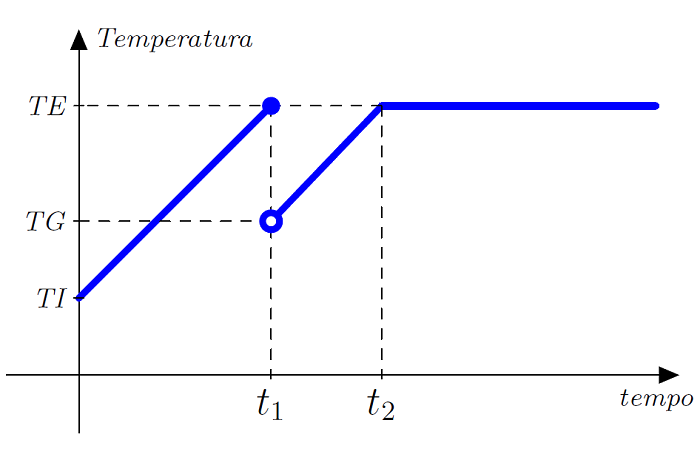
Uma panela com água foi colocada no fogo. No início, a água está em temperatura ambiente ( $T I$ ) e começa a aquecer. No instante em que começa a fervura ( $t_{1}$ ), alguém joga um balde de gelo, provocando uma queda brusca da temperatura, até $T G$ . Poderíamos representar essa situação como no gráfico abaixo.

Depois, a temperatura torna a subir até atingir a temperatura de ebulição, quando se estabiliza.

O que acontece com a temperatura quando o tempo se aproxima de $t_{1}$ ou $t_{2}$ ?

Se, antes do instante $t_{1}$ , fosse possível prever a temperatura em $t_{1}$ , iríamos dizer que a temperatura seria $T E$ , já que a temperatura está se aproximando deste valor antes de $t_{1}$ . Por outro lado, se fosse possível voltar o tempo para trás, e analizar o que acontece com a temperatura quando o tempo volta para $t_{1}$ , diríamos que a temperatura se aproximaria de $T G .$

Esta é a primeira noção de limite que temos, e o que está sendo estimado aqui é o limite à esquerda e à direita da temperatura, quando o tempo se aproxima de $t_{1}$ .

No limite à esquerda, estamos deixando o tempo $t$ se aproximar de $t_{1}$ com valores menores do que $t_{1}$ (à esquerda de $t_{1}$ na reta dos números reais) e vendo o que acontece com a temperatura. Se for possível fazer uma previsão, diremos que o limite da temperatura $T (t)$ quando $t$ tende a $t_{1}$ pela esquerda é o valor da previsão. Escrevemos

lim_{t \to t_{1}^{-}} T (t) = T E,

onde $T (t)$ é a temperatura dada em função do tempo $t$ . Repare no $-$ ao lado do $t_{1}$ , indicando que o limite é à esquerda

Da mesma forma, se aproximamos o tempo de $t_{1}$ com valores maiores que $t_{1}$ (à direita de $t_{1}$ ) e podemos prever que a temperatura se aproxima de um valor, diremos que o o limite de $T (t)$ quando $t$ tende a $t_{1}$ pela esquerda é este valor da previsão. Escrevemos

lim_{t \to t_{1}^{+}} T (t) = T G .

O $+$ ao lado do $t_{1}$ indica que o limite é à direita.

Em qualquer um dos limites acima, à esquerda ou à direita, o valor da função no instante exato $t_{1}$ não interessa. Se tivéssemos $T (t_{1}) = T G$ , os limites seriam os mesmos.

Formalmente, dado um valor fixo $x = a$ , de tal maneira que o conjunto $(a - r, a) \cup (a, a + r)$ está contido no domínio de $f$ , analisamos o comportamento de $f$ nesse conjunto para calcular $lim_{x \to a^{-}} f (x)$ ( lê-se: limite de $f (x)$ quando $x$ tende a $a$ , pela esquerda) e $lim_{x \to a^{+}} f (x)$ (lê-se: limite de $f (x)$ quando $x$ tende a $a$ , pela direita).

O limite à esquerda é verificado analisando o comportamento de $f$ em valores de $x$ menores que $a$ (à esquerda de $a$ na reta numérica), e muito próximos de $a$ . Analogamente, o limite pela direita é verificado analisando o comportamento de $f$ em valores de $x$ maiores que $a$ (à direita de $a$ na reta numérica), e muito próximos de $a$ .

Dizemos que o limite quando $x$ tende a $a$ de $f (x)$ existe e é igual ao número real $L$ , se ambos os limites laterais existem e valem $L$ . Isto é:

lim_{x \to a} f (x) = L \Leftrightarrow lim_{x \to a^{-}} f (x) = lim_{x \to a^{+}} f (x) = L

Exemplo 2

As figuras ??? e ??? apresentam os gráficos das funções $f$ e $g$ . Para cada uma das funções, existem os limites laterais em $x = - 1$ ? O limite existe?

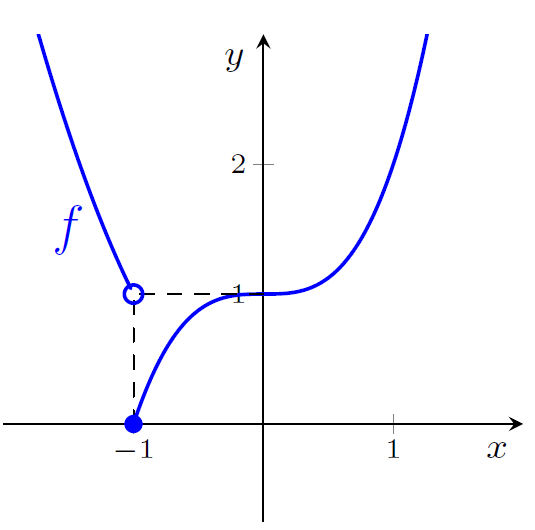
Figura 1: gráfico de $f$

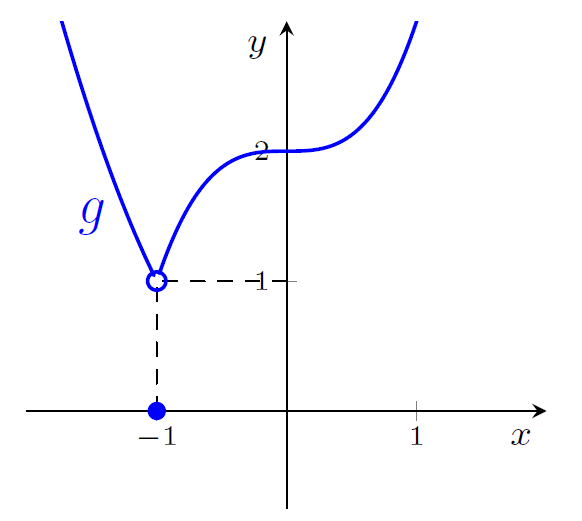
Figura 2: gráfico de $g$

Solução

Para $f (x)$ , fazendo $x$ se aproximar de $- 1$ por valores maiores que $- 1$ , vemos que $f (x)$ se aproxima de $0$ . Portanto, $lim_{x \to {- 1}^{+}} f (x) = 0$ . Para calcular o limite à esquerda, escolhemos valores menores que $x$ cada vez mais próximos de $- 1$ , para concluirmos $lim_{x \to {- 1}^{-}} f (x) = 1$ . Cada um dos limites laterais existe, mas são diferentes. Portanto, não existe $lim_{x \to - 1} f (x)$ . Procedendo de modo análogo para $g (x)$ , vemos que existem os limites laterais, e ambos valem $1$ . Portanto, $lim_{x \to - 1} g (x) = 1$ .

Exemplo 3

Nesse caso, em $x = 3$ , existe o limite à esquerda. O limite à direita não existe em $x = 3$ pois, quando $x$ se aproxima de $3$ pela direita, $f (x)$ não se aproxima de nenhum número, na verdade o valor de $f (x)$ fica tão grande quanto se queira (dizemos que tende a infinito). Assim, como um dos limites laterais não existe, o limite $lim_{x \to 1} f (x)$ não existe.

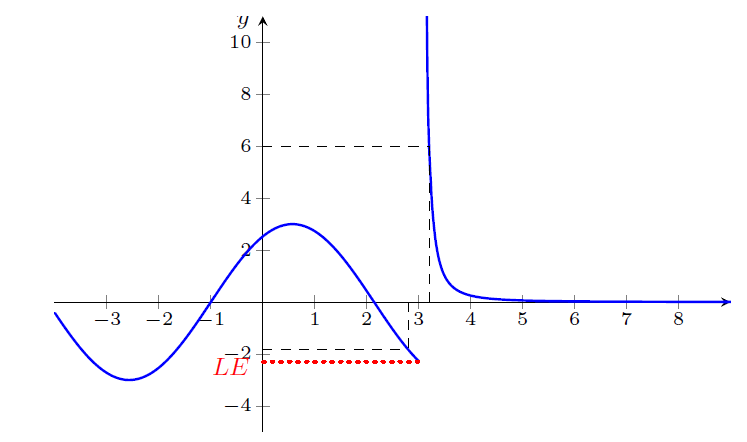
Figura 3: Não Existe o limite à direita em $x = 3$