Calculando Alguns Limites
Apresentamos nesta seção alguns resultados que permitem calcular diversos limites. Antes de prosseguir a leitura, assista ao vídeo abaixo:
Faremos agora um breve resumo esquematizado os resultados vistos no vídeo, resolveremos alguns exemplos e propomos exercícios.
Para algumas funções, sabe-se que, para todo $a$ do domínio, $\displaystyle\lim_{x \rightarrow a}f(x) = f(a)$. Citamos, nesse momento:
- Funções polinomiais
- Funções exponenciais
- Funções trigonométricas em seus domínios
- Funções logarítmicas, $x \in (0, \infty)$
- Funções raízes $n$-ésimas $y=\sqrt[n]{x}$, com $x \in [0, \infty)$ se $n$ for par e $x\in\mathbb{R}$ se $n$ for ímpar.
- Função modular $y=|x|$, $x \in \mathbb{R}$
Este fato será melhor apresentado e devidamente justificado no tópico continuidade. Por enquanto, vamos justificar intuitivamente com o fato de que o gráfico destas funções não apresenta ``quebras" em pontos do domínio.
É importante observar que este fato também vale para os limites laterais, isto é $\displaystyle\lim_{x \rightarrow a^+}f(x) = f(a)$ e $\displaystyle\lim_{x \rightarrow a^-}f(x) = f(a)$.
si
Além disso, também vimos que
Esse resultado é bem conhecido. Sua demonstração poderá ser feita com a introdução da noção formal de limite
Dadas duas funções, $f$ e $g$, tais que $\displaystyle\lim_{x\rightarrow a} f(x) = L_f$ e $\displaystyle\lim_{x\rightarrow a} g(x) = L_g$:
- $\displaystyle\lim_{x\rightarrow a} (f(x) + g(x)) = L_f + L_g$. (Lê-se: o limite da soma é a soma dos limites, caso os limites existam)
- $\displaystyle\lim_{x\rightarrow a} (f(x)\cdot g(x)) = L_f \cdot L_g$. (Lê-se: o limite do produto é o produto dos limites, caso os limites existam)
- Se $L_g \neq 0$, $\displaystyle\lim_{x\rightarrow a} \frac{f(x)}{g(x)} = \frac{L_f}{L_g}$. (Lê-se: o limite do quociente é o quociente dos limites, caso os limites existam e o denominador não tenha limite 0)
Nos primeiros exemplos, vamos justificar cada passo e sugerimos que você também faça isso para firmar a teoria. Com a prática, pode--se assumir como óbvias certas justificativas.
| $\displaystyle\lim_{x\rightarrow 2} e^x (x^3+2x)$ | $=$ | $\displaystyle\lim_{x\rightarrow 2}e^x \cdot \lim_{x\rightarrow 2} (x^3 + 2x)$ | Teorema 1 item (2) |
| $=$ | $12 e^2$ | Observação itens (1) e (2) |
| $\displaystyle\lim_{x \rightarrow 0}\left( \cos(x) + \frac{x^4 + 3x}{\mathrm{sen}(x+\pi/2)}\right)$ | $=$ | $\displaystyle\lim_{x \rightarrow 0} \cos(x) + \displaystyle\lim_{x \rightarrow 0} \frac{x^4 + 3x}{\mathrm{sen}(x+\pi/2)}$ | Teorema 1, item (1) |
| $=$ | $\displaystyle 1 + \dfrac{\displaystyle\lim_{x \rightarrow 0} (x^4 + 3x)}{\displaystyle\lim_{x \rightarrow 0}\mathrm{sen}(x+\pi/2)}$ | Teorema 1 item (3) | |
| $=$ | $\displaystyle 1 + \dfrac{0}{1}$ | Observação itens (2) e (3) | |
| $=$ | $1$ |
Vamos olhar $\displaystyle\lim_{x\rightarrow 1}f(x)$. Se $x \rightarrow 1^-$, $f(x)=x^3 - x^2 + 3 \rightarrow 3$. Se $x \rightarrow 1^+$, $f(x)=2x+5 \rightarrow 7$. A função tem limites laterais diferentes e, portanto, não existe $\displaystyle\lim_{x\rightarrow 1}f(x)$.
Vamos agora discutir um fato bastante intuitivo, e que nasce do próprio conceito de limite.
Sejam $f$ e $g$ funções definidas num intervalo aberto $I$ e seja $a \in I$. Se $f(x)=g(x)$ para todo $x \in I \backslash \{a\}$ e $\displaystyle \lim_{x\to a}g(x) = L$, então $\displaystyle \lim_{x\to a}f(x) = L$.
Note que esta proposição afirma que para comparar o limite de duas funções quando $x \to a$, apenas importa o que acontece em torno de $a$, independente do que possa acontecer em $a$. De fato, poderíamos até generalizar a proposição anterior e considerar que $f$ e $g$ são funções definidas no conjunto $I\backslash \{a\}$.
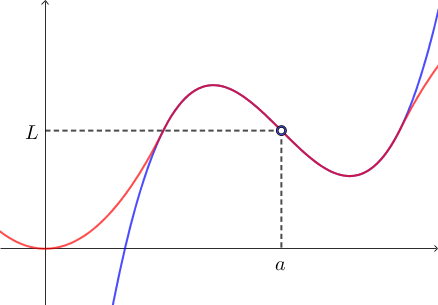
Observe na figura acima. Se duas funções coincidem perto de $x=a$, é natural que tenham o mesmo limite quando $x\to a$.
Este fato será muito utilizado ao longo do curso, e é o que justifica o cálculo de limites através de manipulações algébricas, como veremos no exemplo abaixo.
Calcular
\[\lim_{x\to-2}\frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)}.\]Nossa primeira tentativa seria utilizar o item (3) do Teorema 1 e fazer algo como
\[\lim_{x\to-2}\frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)} = \frac{\lim_{x\to-2} 2x^2+3x-2}{\lim_{x\to-2} (x+2)\;\mathrm{sen}(x)}.\]Mas, como o limite do denominador é 0, não poderíamos ter utilizado o item (3) do Teorema 1.
Uma forma de calcularmos este limite é observar que, perto de $-2$, o numerador e o denominador da fração tendem para $0$. Assim, vemos que é possível fatorar o numerador para reescrever, para $x \neq -2$,
\[\lim_{x\to-2} \frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)} = \lim_{x\to-2} \frac{(2x-1)(x+2)}{(x+2)\;\mathrm{sen}(x)} = \lim_{x\to-2} \frac{(2x-1)\cancel{(x+2)}}{\cancel{(x+2)}\;\mathrm{sen}(x)} = \lim_{x\to-2}\frac{2x-1}{\mathrm{sen}(x)} = \frac{-5}{\mathrm{sen}(-2)}.\]Em nosso curso, lidaremos com vários limites desta forma, e soluções como esta serão aceitas. Porém, é importante entender por que esta forma de calcular um limite está correta. Vamos então refazer as contas anteriores, justificando cuidadosamente com a Proposição 2. Considerando
\[f(x) = \frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)}, x \neq -2 \; \mbox{e} \; x\neq n\pi,\]queremos então calcular
\[\lim_{x\to-2}f(x).\]Para $x \neq -2$, temos
\[f(x) = \frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)} = \frac{(2x-1)\cancel{(x+2)}}{\cancel{(x+2)}\mathrm{sen}(x)} = \frac{2x-1}{\mathrm{sen}(x)}.\]Assim, para $x\neq -2$, $f(x) = g(x) = \dfrac{x+2}{\mathrm{sen}(x)}$. Logo, pela Proposição 2, temos que
\[\lim_{x\to-2}\frac{2x^2+3x-2}{(x+2)\;\mathrm{sen}(x)} = \lim_{x\to-2}f(x) = \lim_{x\to-2}g(x) = \lim_{x\to-2}\frac{2x-1}{\mathrm{sen}(x)} = \frac{-5}{\mathrm{sen}(-2)}.\]Na última igualdade, simplesmente substituímos $x=-2$.
Observe que $\mathrm{sen}(-2)$ é um número (uma calculadora nos dará uma boa aproximação), então já chegamos ao valor do limite. Não precisamos aqui calcular $\mathrm{sen}(-2)$.
Na última seção deste texto, veremos outros exemplos de limites em que utilizaremos fatoração e outras manipulações algébricas, sempre justificando a aplicabilidade destas manipulações pela Proposição 2.
Um segundo ponto, que discutimos no vídeo, foi a relação entre o limite de duas funções, $f$ e $g$ e o limite da composta: $f\circ g$. Como sempre, quando se trata de composição, precisamos entender a ordem com que as operações são feitas. Se estamos falando de $f \circ g (x)$, para cada $x$, primeiro calculamos $g$ para obter um valor e, depois, calculamos $f$ desse valor. Esquematicamente:
\[x \stackrel{g} \mapsto g(x) \stackrel{f} \mapsto f(g(x))\]Então, se queremos $\displaystyle\lim_{x \rightarrow a} f\circ g(x)$, precisamos calcular o limite quando $x$ tende a $a$ de $g$, e obter um valor $\ell$. Depois, precisamos estudar o que acontece com a função $f$ perto de $\ell$ e não de $a$. Esquematicamente:
\[\begin{array}{ccccc}x &\stackrel{g}\longmapsto & g(x)& \stackrel{f} \longmapsto & f(g(x))\\\downarrow & & \downarrow & & \downarrow \\a &\stackrel{\lim_{x\rightarrow a} g(x)} \longrightarrow & \ell & \stackrel{\lim_{x \longrightarrow \ell} f(x) }\longrightarrow & \mbox{???}\end{array} \]Formalmente, enunciamos o resultado:
Se $\displaystyle\lim_{x\rightarrow a} g(x) = \ell$, $\displaystyle\lim_{x \rightarrow \ell}f(x)=L$ e $\ell \notin D(f)$, então $\displaystyle\lim_{x \rightarrow a} f\circ g (x) = L$.
Observação: No teorema anterior, estamos supondo que existe $r >0$ tal que $(a-r,a) \cup (a,a+r) \subset D(g)$ e $g(x) \neq \ell, \, \forall x \in (a-r,a) \cup (a,a+r)$.
Suponha que $f(x)$ é uma função, tal que $\displaystyle\lim_{x \rightarrow 1} f(x) = 3$, $\displaystyle\lim_{x \rightarrow 0} f(x) = \sqrt{3}$ e
$\displaystyle\lim_{x \rightarrow -2} f(x) = 5$. Seja $g(x) = 3x -2$, $x \in \mathbb R$. Quanto vale $\displaystyle\lim_{x \rightarrow 0} f \circ g(x)$?
Representando no esquema:
\[\begin{array}{ccccc}x &\stackrel{g}\longmapsto & 3x-2& \stackrel{f} \longmapsto & f(3x-2)\\\downarrow & & \downarrow & & \downarrow \\0 &\stackrel{\lim_{x\rightarrow 0} 3x-2} \longrightarrow & -2 & \stackrel{\lim_{x \longrightarrow -2} f(x) }\longrightarrow & 5\end{array}\]Formalmente $\displaystyle\lim_{x \rightarrow 0}g(x) = -2$ e $\displaystyle\lim_{x \rightarrow -2} f(x) = 5 \Rightarrow \displaystyle\lim_{x \rightarrow 0} f \circ g(x) = 5$.
O Teorema 2 nos fornece uma técnica muito importante para o cálculo de limites, conhecida como substituição de variável. Para calcular o limite
\[\lim_{x \to a}f\left(g(x)\right),\]sabendo que $\displaystyle\lim_{x \to a} g(x) = \ell$, definimos $u = g(x)$ e, temos então
\[\lim_{x \to a}f\left(g(x)\right) = \lim_{u \to \ell}f(u)=L,\]que pode ser um limite muito mais simples de calcular. É muito importante se lembrar, de, além de trocarmos $g(x)$ por $u$, trocarmos o ponto no qual calculamos o limite, isto é, trocar $x\to a$ por $u\to \ell$.
Esta técnica é justificada pelo Teorema 2, pois ele afirma que, se $\displaystyle\lim_{x \to a} g(x) = \ell$ e $\displaystyle\lim_{x \to \ell}f(x) = L$ então
\[\lim_{x \to a}f\left(g(x)\right) = \lim_{x \to \ell}f(x),\]que é a mesma coisa que escrever $\displaystyle \lim_{u \to \ell}f(u)$, apenas estamos renomeando a variável.
Sabendo que $\displaystyle\lim_{x\to 0} f(x) = 2$, calcular
\[\lim_{x\to 1}\frac{f(x-1)}{x+1}.\]Podemos fazer $u = x-1$. Com isso, $x=u+1$, logo, o denominador pode ser reescrito como $x+1 = u+1+1 = u+2$. Além disso, temos $\displaystyle\lim_{x\to 1} (x-1) = 0$, logo $u\to 0$ quando $x\to 1$. Assim,
\[\lim_{x\to 1}\frac{f(x-1)}{x+1} = \lim_{u\to 0}\frac{f(u)}{u+2}=\frac{\displaystyle\lim_{u\to 0} f(u)}{\displaystyle\lim_{u\to 0} u+2} = \frac{2}{2}=1.\]
Sabendo que $\displaystyle\lim_{x\to 0} f(x) = 2$, calcular
\[\lim_{x\to 2}\frac{f(2x^2-8)}{x^2} .\]
Podemos fazer $u = 2x^2-8$. Com isso, $2x^2=u+8$ e então $x^2=\frac{u}{2}+4$. Além disso, temos $\displaystyle\lim_{x\to 2} 2x^2-8 = 0$, logo $u\to 0$ quando $x\to 2$. Assim,
\[\lim_{x\to 2}\frac{f(2x^2-8)}{x^2} = \lim_{u\to 0}\frac{f(u)}{\frac{u}{2}+4} = \frac{\displaystyle \lim_{u\to 0}f(u)}{\displaystyle \lim_{u\to 0}\frac{u}{2}+4} = \frac{2}{4}=\frac{1}{2}.\]
Vários outros exemplos serão vistos na última seção, quando utilizaremos susbstituição de variável para calcular alguns limites envolvendo funções trigonométricas.
Considere:
\[f(x) = \begin{cases} 3x+ 5,&\text{se } x <2 \\x^2,&\text{se } x>2 \end{cases} \;\; \text{ e } \;\; g(x) = \begin{cases} 2x,& \text{se } x <1 \\ 2x+2,& \text{se } x>1 \end{cases} \]Estude $\displaystyle\lim_{x \rightarrow 1} f \circ g(x)$.
se $x\rightarrow 1^-$, $g(x) \rightarrow 2^-$, porque para valores de $x$ menores que $1$, $g(x) = 2x$ e se $x<1$, $2x <2$. Se $x \rightarrow 2^-$, $f(x) \rightarrow 11$. Portanto, $\displaystyle\lim_{x \rightarrow 1^-} f\circ g(x) = 11$. Se se $x\rightarrow 1^+$, $g(x) \rightarrow 4$ e $\displaystyle\lim_{x \rightarrow 4} f(x) = 16$. Portanto $\displaystyle\lim_{x \rightarrow 1^+} f\circ g(x) = 16$. Conclusão: Não existe o limite da composta em $x=1$, porque os limites laterais são diferentes.

