Definição Formal

Atenção! Esta seção trará uma maior formalização do conceito de limite, e você deve ler com o objetivo de consolidar este conceito. Porém, não deve se preocupar em, necessariamente, saber reproduzir as ideias ou conseguir saber tratar, sozinho, os exemplos apresentados.

Antes de prosseguir, sugerimos que você assista ao vídeo Uma definição clássica de limite.

Até o momento, estudamos limites de uma forma intuitiva. A ideia fundamental é que

\[\lim_{x\rightarrow a} f(x) = L\]

se for possível verificar que o valor de $f(x)$ fica muito ``próximo’’ do número real $L$ quando $x$ se ``aproxima’’ de $a$. Infelizmente, o significado de ``estar próximo’’ pode variar muito; quando $x \rightarrow 1$, $3x$ está próximo de $3$, mas também está próximo de $2,\!99$, de $3,\!01$, e queremos um conceito de limite que torne o valor $3$ (nesse caso) único. Queremos que $3$ seja o limite e não um limite.

Imagine que alguém quer percorrer uma distância fixa, a partir de um ponto, marcado como $0$, usando a seguinte regra: cada passo deve ter exatamente metade da distância que falta. Não é difícil perceber que essa pessoa nunca atingirá o destino, mas chegará muito perto. Quão perto? Tanto quanto deseje, desde que disponha de tempo ``suficiente’’ para caminhar. Se pensarmos que a posição dessa pessoa no caminho é uma função que depende do tempo, $P(t)$, vemos que a imagem dessa função se aproxima tanto quanto se queira de um valor determinado (nesse caso, o ponto de chegada), se o domínio - os valores possíveis de $t$ - for escolhido de forma conveniente. Reside aqui a essência da concepção de limite: a imagem da função precisa se aproximar do limte, tanto quanto se queira, ainda que para isso seja preciso restringir o domínio.

É crucial termos uma definição precisa do que vem a ser tão perto quanto se queira. A noção de perto $\times$ longe, depende de uma medida de distância. Em $\mathbb R$, medimos a distância entre dois pontos, $p_1$ e $ p_2$, como $|p_1 - p_2|$. Em ``matematiquês’’, quando se quer dizer que alguma coisa pode se tornar tão pequena quanto se queira, é comum estabelecer que ela pode ser feita menor do que qualquer valor positivo. Assim, quando se quer garantir que alguma grandeza pode ficar arbitrariamente pequena, dizemos que esta grandeza pode se tornar - sob determinadas condições - menor do que $\epsilon$ (lê-se epsilon), para qualquer $\epsilon$ maior do que $0$. A letra $\epsilon$ está sendo usada aqui por uma questão de tradição mas, evidentemente, serviria qualquer símbolo} Aqui, queremos que a distância entre uma função e seu limite se torne tão pequena quanto se queira, então, vamos dizer que o limite será $l$ se $|f(x) - l| < \epsilon$, para todo $\epsilon >0$, desde que sejam escolhidos valores convenientes de $x$.

Vamos olhar para o exemplo inicial, $f(x) = 3x$. O meu candidato a limite quando $x$ tende a $1$ é $3$. Preciso garantir que $|3x -3| $ seja menor que qualquer $\epsilon$ positivo, desde que eu possa escolher quão perto $x$ está de $1$. Começo tentando $\epsilon = 1/2$. Escrevo um ``rascunho’’:

Será que $|3x -3| < 1/2$, se $x$ estiver bem perto de $1$? Posso escrever $|3x-3|$ como $3|x-1|$ e analiso: $|3x-3| = 3|x-1|<1/2 $? Bem, se $|x-1| <1/6$ vai dar certo. Vou fingir que não fiz rascunho nenhum e volto ao texto.

Se $\epsilon = 1/2$, escolho $|x-1| < 1/6$.

\[|x-1| < 1/6 \Leftrightarrow 3|x-1| < 3/6 \Leftrightarrow |3x-3|<1/2\]

e mostro que a distância entre $f(x)$ e o limite pode ser menor que $\epsilon = 1/2$ desde que eu escolha $x$ no intervalo $(1-1/6, 1+1/6)$. Ou seja, a distância entre $x$ e $1$ não pode ser maior que $1/6$.

Mas o resultado tem que valer para $\epsilon$ tão pequeno quanto se queira. Vou tentar com $\epsilon = 1/10$. Mais um rascunho:

Será que $|3x -3| < 1/10$, se $x$ estiver bem perto de $1$? Posso escrever $|3x-3|$ como $3|x-1|$ e analiso: $|3x-3| = 3|x-1|<1/10 $? Bem, se $|x-1| <1/30$ vai dar certo. Vou fingir que não fiz rascunho nenhum e volto ao texto.

Se $\epsilon = 1/10$, escolho $|x-1| < 1/30$.

\[|x-1| < 1/30 \Leftrightarrow 3|x-1| < 3/30 \Leftrightarrow |3x-3|<1/10\]

e mostro que a distância entre $f(x)$ e o limite pode ser menor que $\epsilon = 1/10$ desde que eu escolha $x$ no intervalo $(1-1/30, 1+1/30)$ Ou seja, a distância entre $x$ e $1$ não pode ser maior que $1/30$.

Bem, vamos tentar com um $\epsilon$ qualquer. Novo rascunho:

Será que $|3x -3| < \epsilon $, se $x$ estiver bem perto de $1$? Posso escrever $|3x-3|$ como $3|x-1|$ e analiso: $|3x-3| = 3|x-1|< \epsilon $? Bem, se $|x-1| <\epsilon/3$ vai dar certo. Vou fingir que não fiz rascunho nenhum e volto ao texto.

Seja $\epsilon$ maior que $0$ dado. Escolha $x$ tal que $|x-1|<\epsilon/3$. Então:

\[|x-1| < \frac{\epsilon}{3} \Leftrightarrow 3|x-1| < \frac{3\epsilon}{3} \Leftrightarrow |3x-3|<\epsilon\]

Esse procedimento sugere que podemos dizer que o $\displaystyle\lim_{x \rightarrow a} f(x) = l $ se e somente se para todo $\epsilon >0$ é possível determinar um intervalo em torno de $a$, tal que se $x$ está nesse intervalo, $|f(x) - l | < \epsilon$.

É comum substituir a expressão ``é possível determinar um intervalo em torno de $a$’’ por um modo mais conciso de afirmar a mesma coisa: diz-se que existe um $\delta>0$ (delta) tal que $|x-a| < \delta$. (Note que $|x-a| < \delta $ é equivalente a $ x \in (a-\delta, a+\delta)$. Então dizemos que o $\displaystyle\lim_{x \rightarrow a} f(x) = l $ se, e somente se, para todo $\epsilon >0$ é possível determinar um $\delta>0$, tal que se $|x-a|<\delta$, $|f(x) - l | < \epsilon$. Nesse ponto, incorporamos mais um detalhe: para efeito do cálculo do limite quando $x$ tende a $a$, o que acontece exatamente no ponto $a$ não é relevante; $a$ pode nem estar no domínio da função. Para incorporar esse fato, vamos nos restringir ao conjunto $(a - \delta,a) \cup (a, a+ \delta)$ ou, equivalentemente, vamos escrever que $0 < |x-a| < \delta $.

Temos agora os pré-requisitos para apresentar a famosíssima definição formal de limite por epsilons e deltas.

Definição 1

Dizemos que limite quando $x$ tende a $a$ de uma função $f(x)$ é igual ao número real $L$ se e somente se: para todo $\epsilon>0$ existe um $\delta >0 $, tal que, se $0<|x-a| < \delta$, então $|f(x) - L| < \epsilon $.

Em ``matematiquês’’ puro e castiço, fica:

\[\displaystyle\lim_{x \rightarrow a} f(x) = L \iff \forall \epsilon >0, \;\exists \delta >0, \text{tal que, se } 0< |x-a|< \delta \; \Rightarrow \;|f(x) -L| < \epsilon \]

A segunda parte da Definição 1 exemplifica bem as maravilhas e os horrores do matematiquês. Quem tem prática, consegue escrever de forma simples, curta e clara o que quer dizer. Quem não pratica, quando vai ler um texto técnico, encontra um monte de ``símbolos sem nexo’’. É sempre bom praticar. Ajuda a escrever, a ler, a pensar e a entender. Podemos olhar a interpretação gráfica da Definição 1 na Figura 1:

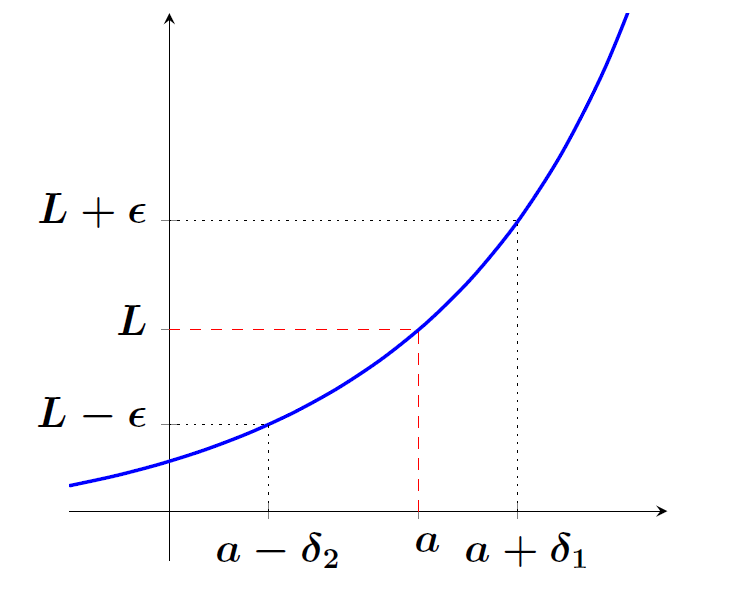
Figura 1: A imagem de $f$ em pontos próximos de $a$
está em um intervalo de raio $\epsilon$ em torno de $L$.

Definido um valor de $\epsilon$, verificamos que a imagem de $f$, em algum conjunto $(a-\delta_2, a) \cup (a, a+ \delta_1)$ em torno de $a$, está contida em uma faixa de raio $\epsilon$ em torno de $L$. Para efeito da definição, podemos escolher $\delta $ como o mínimo entre os dois, ou seja, $\delta=\min (\delta_1, \delta_2)$.

A definição formal de limite é bastante útil para fazer várias demonstrações; infelizmente, seu uso nem sempre é muito fácil porque ``descobrir o $\delta$ e mostrar que funciona’’ pode dar muito trabalho. Nesse texto, vamos fazer alguns exemplos do seu uso.

O próximo Teorema responde nossa pergunta inicial. Ele mostra que só pode existir um valor que satisfaz a defininição de limite. Apresentamos a demonstração numerando os passos e justificamos cada etapa logo depois.

Teorema 1

Seja $f(x)$ uma função real e suponha que existe um $r$ tal que o conjunto $(a-r,a) \cup (a, a+r)$ está contido no domínio de $f$. Se existe o limite quando $x$ tende a $a$ de $f(x)$, ele é único

Demonstração

Suponha que existem $l_1$ e $l_2$ tais que $\displaystyle \lim_{x \rightarrow a}f(x) = l_1$ e $\displaystyle \lim_{x \rightarrow a}f(x) = l_2$.
Basta mostrar que $|l_1 -l_2| < \epsilon $, $\forall \epsilon>0$.
Seja $\epsilon > 0$ dado e sejam $\delta_1$ e $\delta_2$ tais que se $ 0< |x- a| < \delta_1 \Rightarrow |f(x) - l_1| < \epsilon/2 $ e $ 0< |x- a| < \delta_2 \Rightarrow |f(x) - l_2| < \epsilon/2 $.
Escolha $\delta = \min (\delta_1, \delta_2)$.
Escolha $x$ tal que $0 < |x-a| < \delta $.
Para um tal $x$, $|l_1 - l_2| = | l_1 - f(x) + f(x) - l_2| \leq |l_1 - f(x)| + |f(x) - l_2| < \epsilon/2 + \epsilon/2 = \epsilon $.

Justificando cada passo:

Para mostrar que só pode existir um único valor, é comum começar supondo que existem dois, e provar que eles são iguais.
Como $l_1$ e $l_2$ são números fixos, se a diferença entre eles for menor que qualquer valor positivo, será zero, o que permite concluir que são iguais.
Os valores de $\delta_1$ e $\delta_2$ devem existir pela definição de limite.
Escolhemos o menor valor dentre os $\delta$s para que atenda a definição tanto para $l_1$ quanto para $l_2$.
Aqui, fixamos um $x$ no intervalo adequado apenas para utilizar o valor $f(x)$ como auxiliar na estimativa subsequente.
Somamos e subtraimos $f(x)$ como um recurso algébrico sem maior sentido. Apenas para usar a desigualdade $|a+b|\leq |a|+|b|$ como é feito nesse mesmo item. Ao escrever desse modo, a definição de limite permite fazer a estimativa adequada.

O Teorema ??? a seguir, que foi visto no texto anterior, é conhecido como Teorema do Anulamento. Ele afirma que, se uma função $g$ limitada é multiplicada por outra função $f$ que tende a zero em um ponto $x =a$, então produto de $f$ por $g$ tende a zero em $x=a$. Usamos esse resultado para estudar $\displaystyle \lim_{x\rightarrow 0} x\cdot \mathrm{sen}\frac{1}{x}$ e vários outros exemplos.

Teorema 2

(Anulamento) Seja $g(x)$ uma função limitada em algum intervalo em torno de $a$, exceto, possivelmente, no próprio $a$, ou seja, $|g(x)|\leq M, \forall x \in (a-r,a)\cup (a,a+r)$,para algum $r>0$. Se $\displaystyle \lim_{x\rightarrow a} f(x) =0$, então $\displaystyle \lim_{x \rightarrow a} f(x)g (x) = 0$.

Demonstração

Preciso mostrar que $\forall \epsilon>0$, $\exists \delta>0$, tal que $0<|x-a| < \delta \Rightarrow |f(x)g(x)|< \epsilon$.
Seja $\epsilon >0$ dado e escolha $\delta_1>0$, tal que $0<|x-a|< \delta_1 \Rightarrow |f(x)|< \frac{\epsilon}{M}$
$|f(x)g(x)|= |f(x)| |g(x)| < M|f(x)|$, $\forall x \in (a-r,a)\cup (a,a+r)$.
Se $0<|x-a| < \delta$, $|f(x)| < \epsilon/M$. Portanto, $|f(x)g(x)|<|f(x)| |g(x)| < M|f(x)| < M. \frac{\epsilon}{M} = \epsilon$, $\forall x \in (a-\delta,a)\cup (a,a+\delta)$, $\delta=min(\delta_1,r)$.

Justificando cada passo:

Decorre diretamente da definição de limite.
Dado $\epsilon>0$, $\epsilon/M$ é um valor positivo e, pela definição de limite, é possível achar $\delta_1>0$ tal que se $0<|x-a|< \delta_1$, então $|f(x)|< \epsilon/M$.
$|f(x) g(x)| = |f(x)| |g(x)|$ sempre! E $|f(x)|.|g(x)| < M |f(x)|$, $\forall x \in (a-r,a)\cup (a,a+r)$, pois por hipótese, $|g(x)|<M$, $\forall x \in (a-r,a)\cup (a,a+r)$.
Decorre diretamente dos passos anteriores.

Como último exemplo vamos mostrar uma das propriedades básicas de limite: O limite da soma é a soma dos limites.

Teorema 3

Sejam $f$ e $g$ duas funçãos reais definidas em algum intervalo em torno de $a$, exceto, possivelmente, em $a$. Suponha que $\displaystyle \lim_{x \rightarrow a} f(x) = lf$ e que $\displaystyle \lim_{x \rightarrow a} g(x) = lg$. Então $\displaystyle\lim_{x \rightarrow a} (f+g)(x) = lf + lg$.

Demonstração