O Teorema do Confronto
Calcular o limite $\displaystyle \lim_{x\to0}\frac{\mathrm{sen}(x) + x^3(1+\cos(10x)) }{x}$, caso exista.
Observe que, para todo $x\neq 0$,
\[\frac{\mathrm{sen}(x) + x^3(1+\cos(10x)) }{x} = \frac{\mathrm{sen}(x)}{x} + \frac{x^3(1+\cos(10x)) }{x}= \frac{\mathrm{sen}(x)}{x} + x^2(1+\cos(10x))\]Assim, fazendo
\[f(x) = \frac{\mathrm{sen}(x) + x^3(1+\cos(10x)) }{x},\]para todo $x\neq 0$, teremos
\[f(x) = \frac{\mathrm{sen}(x)}{x} + x^2(1+\cos(10x)).\]Observe que a função $\cos$ é limitada, assumindo valores no intervalo $[-1,1]$. Assim, $-1 \leqslant \cos(10x) \leqslant 1$, temos $0 \leqslant 1+\cos(10x) \leqslant 2$, e, portanto
\[\frac{\mathrm{sen}(x)}{x} \leqslant f(x) \leqslant \frac{\mathrm{sen}(x)}{x} + 2x^2.\]Definindo, para todo $x \neq 0$,
\[g(x) = \frac{\mathrm{sen}(x)}{x},\]\[h(x) = \frac{\mathrm{sen}(x)}{x} + 2x^2,\]
teremos, para $x\neq 0$,
\[g(x) \leqslant f(x) \leqslant h(x).\]Vamos agora calcular, caso existam, os limites de $g$ e $h$ com $x$ tendendo a 0. Temos
\[\lim_{x\to0}g(x) = \lim_{x\to 0}\frac{\mathrm{sen}(x)}{x} = 1,\]\[\lim_{x\to0}h(x) = \lim_{x\to 0}\left(\frac{\mathrm{sen}(x)}{x} + 2x^2\right) =\lim_{x\to 0}\frac{\mathrm{sen}(x)}{x} + \lim_{x\to 0} 2x^2= 1 + 0 = 1.\]
Assim, $g$ e $h$ têm o mesmo limite 1 quando $x$ tende a 0.
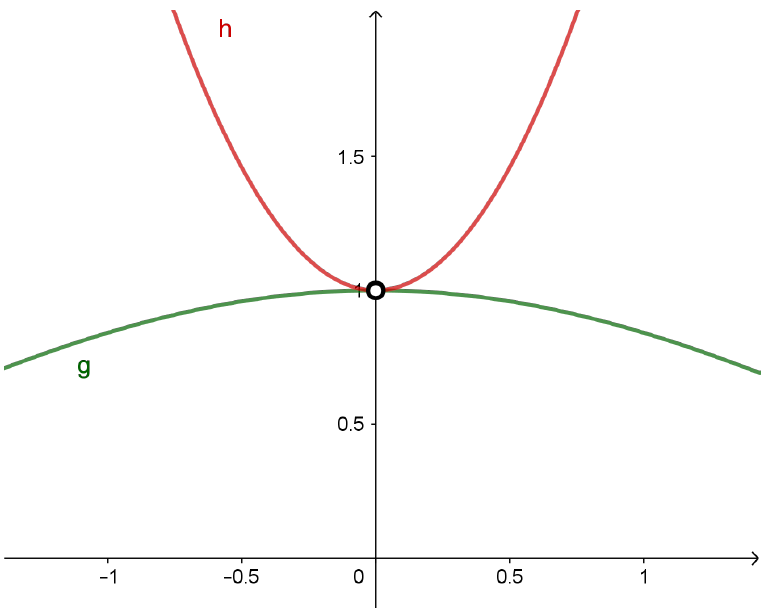
Mas lembre-se de que $g(x) \leqslant f(x) \leqslant h(x)$ para todo $x\neq 0$. Assim, a função $f$ terá seu gráfico compreendido entre os gráficos de $g$ e $h$, como mostrado abaixo.
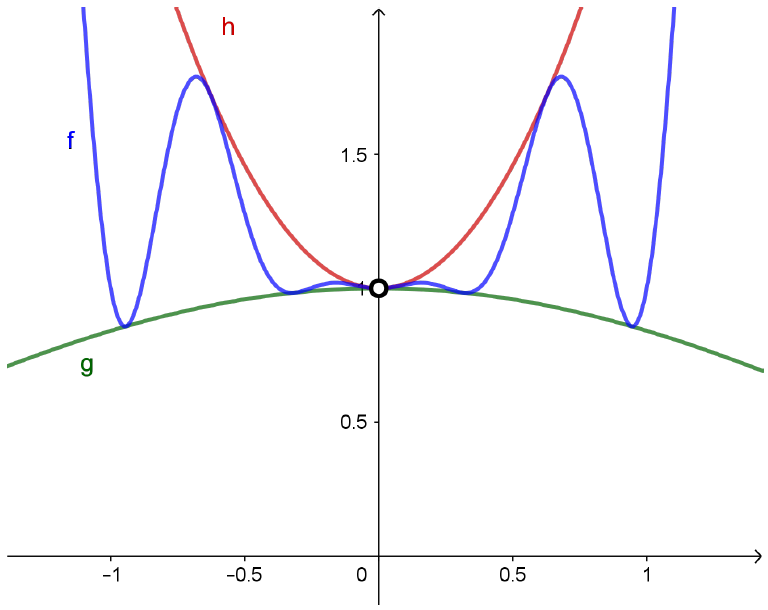
É razoável acreditarmos que
\[\lim_{x \to 0} g(x) \leqslant \lim_{x \to 0} f(x) \leqslant \lim_{x \to 0}h(x),\]e, como $\displaystyle \lim_{x \to 0} g(x) = \lim_{x \to 0} h(x) = 1$, teremos
\[1 \leqslant {\lim_{x \to 0}}f(x) \leqslant 1,\]logo
\[\lim_{x\to 0} f(x) = 1.\]
Teorema do Confronto
O que nos pareceu intuitivo no exemplo anterior é garantido pelo Teorema que enunciamos abaixo.
Sejam $f$, $g$ e $h$ três funções definidas próximas de $a\in\mathbb{R}$, mas que não precisam estar definidas em $a$, isto é, definidas em $(a-r,a) \cup (a,a+r)$, para algum $r>0$. Se
\[g(x) \leqslant f(x) \leqslant h(x)\]para todo $x \in (a-r,a) \cup (a,a+r)$, e
\[\lim_{x\to a}g(x) = \lim_{x\to a}h(x) = L,\]então
\[\lim_{x\to a}f(x) = L.\]
Vamos entender o enunciado deste Teorema. Primeiro, temos três funções $f, g$ e $h$ tais que
\[g(x) \leqslant f(x) \leqslant h(x)\]para todo $x$ próximo a $a \in R$, mas não importando o que aconteça para $x=a$. Na verdade, as funções nem precisam estar definidas em $x=a$. Agora, suponha que as funções $g$ e $h$ tenham o mesmo limite $L$ quando $x$ tende a $a$, isto é,
\[\lim_{x\to a}g(x) = \lim_{x\to a}h(x) = L.\]
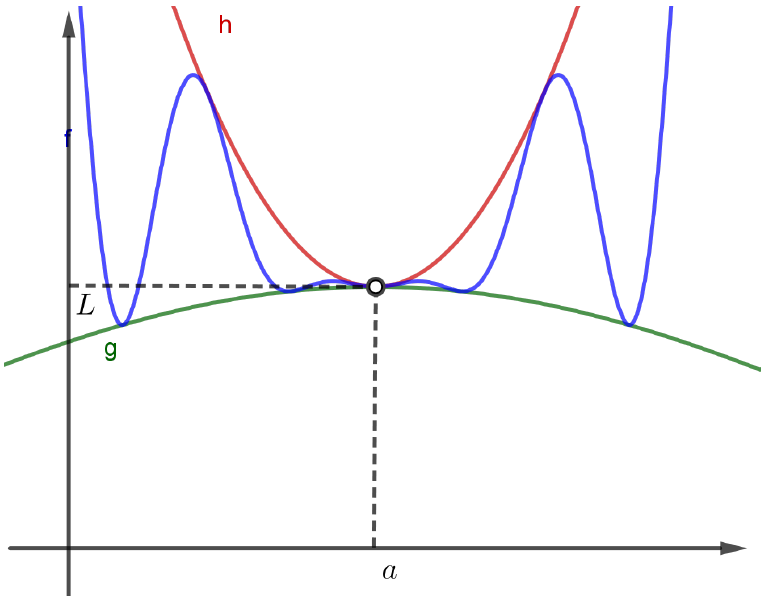
Isto significa que, perto de $x=a$, as funções $g$ e $h$ estão ``espremendo’’ a função $f$, fazendo com que ela tenha, também, o mesmo limite $L$ em $x=a$, isto é,
\[\lim_{x\to a}f(x) = L.\]No esboço que acabamos de apresentar, parece que temos $g(x) \leqslant f(x) \leqslant h(x)$, para todo $x\neq a$. Isto não precisa acontecer para podermos chegar à conclusão do Teorema. Veja o esboço abaixo:
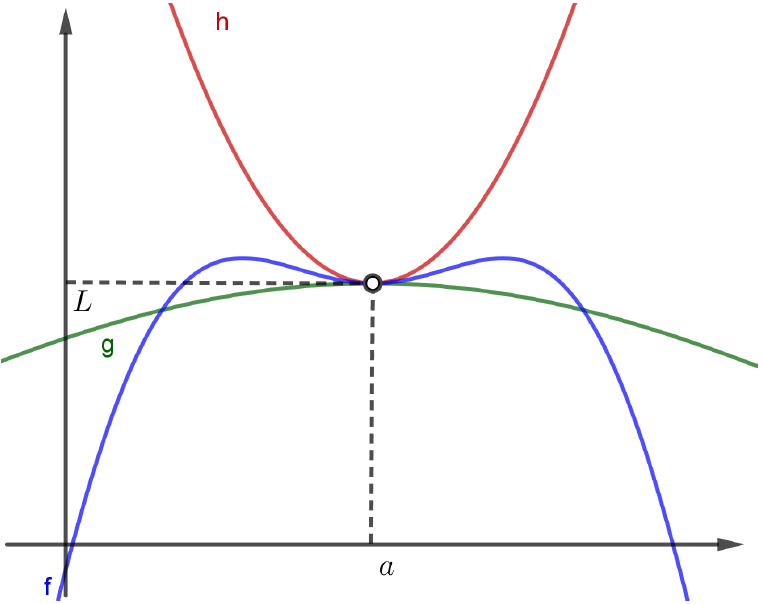
Neste esboço, claramente não é verdade que $g(x) < f(x)$ para todo $x \in \mathbb{R}-\{a\}$. De fato, se nos afastarmos de $x=a$, podemos ver que o valor de $f(x)$ é menor que $g(x)$.
Porém, lembre-se de que, para limites, o importante é o que acontece perto do ponto onde estamos estudando o limite. Neste caso, se nos restringirmos a valores próximos a $x=a$, como no esboço abaixo, a condição $g(x) \leqslant f(x) \leqslant h(x)$ será satisfeita; observe:
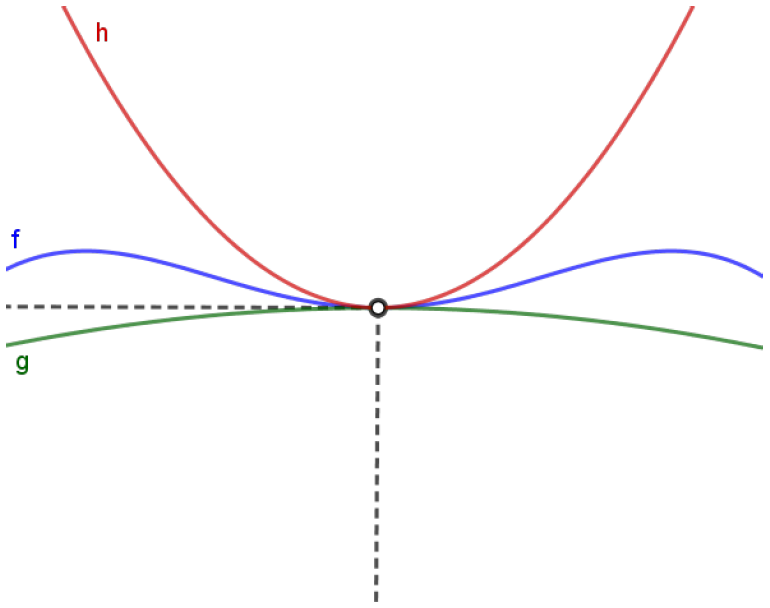
Teremos, de acordo com o Teorema do Confronto,
\[\lim_{x\to a}f(x) = L.\]Há um outro ponto que precisamos destacar. Você deve se lembrar de que, para a existência e para o cálculo do $\displaystyle \lim_{x\to a}f(x)$, o valor que $f(a)$ é absolutamente irrelevante. Na verdade, este valor sequer precisa estar definido. Isto se aplica também ao Teorema do Confronto. Releia o enunciado e veja que fizemos questão de destacar que as funções precisam estar definidas perto de $x=a$, mas não necessariamente em $x=a$. Além disso, a condição $g(x) \leqslant f(x) \leqslant h(x)$ também só foi exigida para todo $x$ perto de $a$ com $x\neq a$. Se esta condição vale ou não vale em $a$, é absolutamente irrelevante para a conclusão do Teorema. Observe o esboço abaixo:
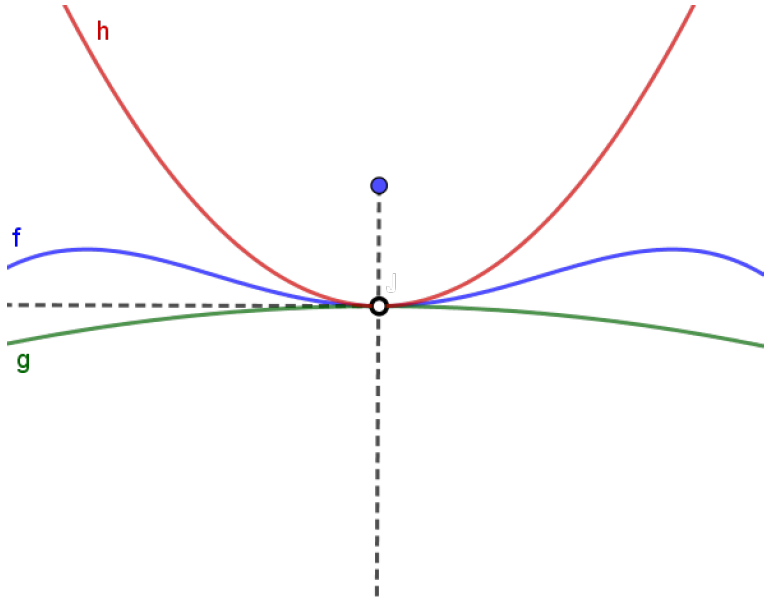
Repare que temos todas as condições satisfeitas:
\[\left\{\begin{array}{l}g(x) \leqslant f(x) \leqslant h(x), x \text{ próximo de } a, x \neq a\\\;\\ \displaystyle \lim_{x \to a} g(x) = \lim_{x\to a} h(x) = L\end{array}\right.\]Portanto, pelo Teorema do Confronto,
\[\lim_{x\to a} f(x) = L.\]
Uma divertida (eu pelo menos acho divertida!) observação sobre o Teorema do Confronto é que ele também é bastante (mesmo!) conhecido como Teorema do Sanduíche. Este nome é muito sugestivo do que acontece, uma vez que temos as funções $g$ e $h$ ensanduichando a função $f$. Observe, porém, que este sanduíche de funções deve ter sido comprimido em $x=a$, a ponto de as fatias $g$ e $h$ encontrarem.
Outras versões do Teorema do Confronto
Considere a situação do esboço abaixo,
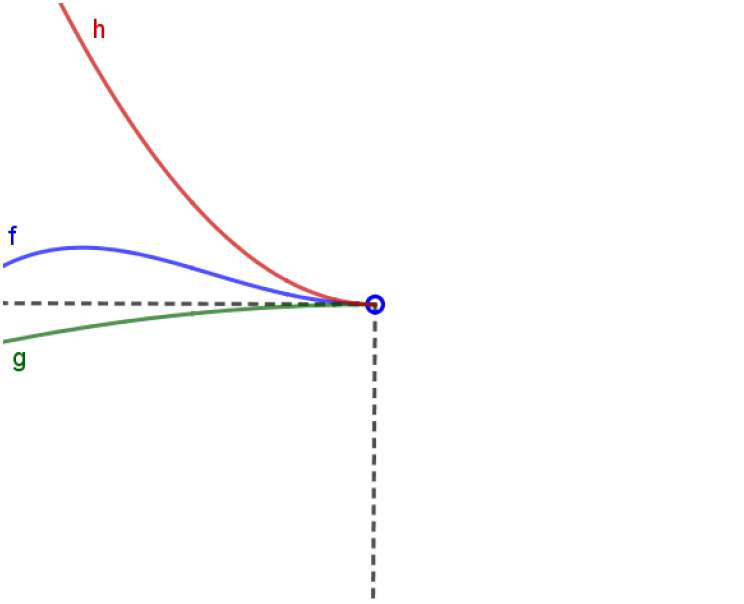
isto é, $g(x) \leqslant f(x) \leqslant h(x), \text{para todo } x \text{ próximo de } a, \text{ com } x < a$, e $\lim_{x \to a^-} g(x) = \lim_{x\to a^-} h(x) = L$.
A mesma intuição que nos faz acreditar no Teorema do Confronto que apresentemos anteriormente também nos permite concluir que
Esta seria uma versão ``à esquerda’’ do Teorema do Confronto. Não temos a menor ideia do que acontece à direita de $x=a$. Poderíamos até ter uma situação como abaixo:
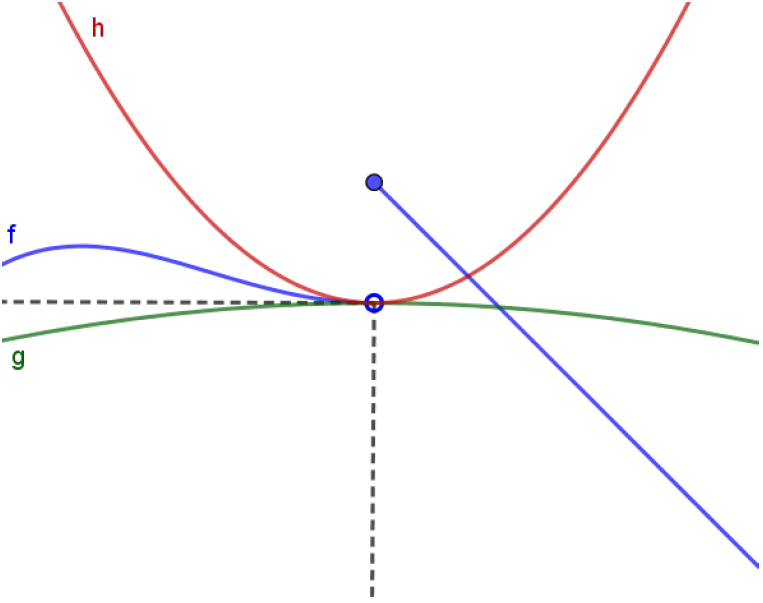
Mas, se restringirmos nosso estudo ao que acontece à esquerda de $x=a$, o limite $\lim_{x\to a^-} f(x) = L$ estaria garantido.
Temos então a seguinte versão ``lateral’’ do Teorema:
Sejam $f$, $g$ e $h$ funções definidas para todo $x$ próximo à esquerda de $a$, ou seja, para $x\in(a-r,a)$, para algum $r>0$. Se
\[g(x) \leqslant f(x) \leqslant h(x)\]para todo $x\in (a-r,a)$, e
\[\lim_{x\to a^-}g(x) = \lim_{x\to a^-}h(x) = L,\]então
\[\lim_{x\to a^-}f(x) = L.\]
Fizemos questão de repetir, no enunciado do Teorema, que a desigualdade só precisa valer ``para todo $x$ próximo a $a$ com $x < a$’’. Isto porque, mais uma vez, só importa o que acontece perto e à esquerda de $x=a$.
Analogamente, podemos enunciar uma versão ``à direita’’:
Sejam $f$, $g$ e $h$ funções definidas para todo $x$ próximo à direita de $a$, ou seja, para $x\in(a,a+r)$, para algum $r>0$. Se
\[g(x) \leqslant f(x) \leqslant h(x)\]para todo $x\in(a,a+r)$, e
\[\lim_{x\to a^+}g(x) = \lim_{x\to a^+}h(x) = L,\]então
\[\lim_{x\to a^+}f(x) = L.\]
O esboço abaixo ilustra bem o que este Teorema significa:
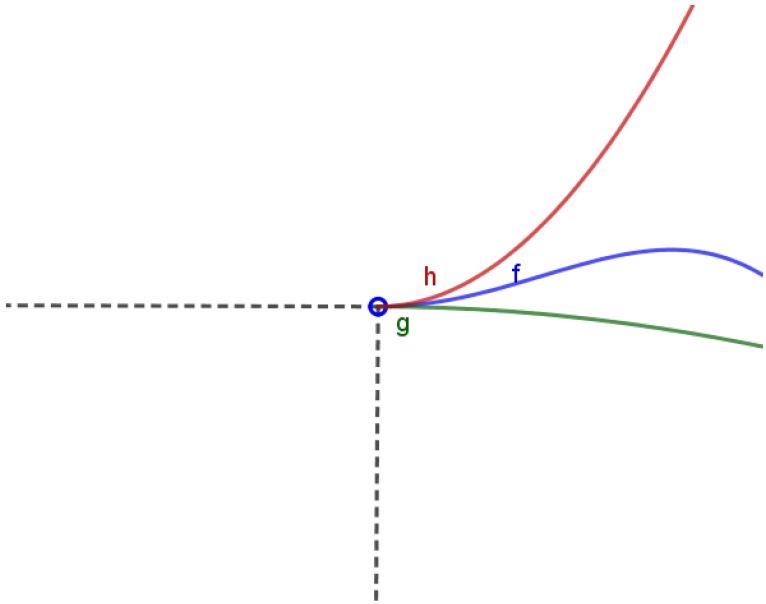
É fácil acreditarmos que, nas condições do Teorema anterior,
\[\lim_{x\to a^+}f(x) = L.\]Poderíamos ter algo como a figura abaixo:
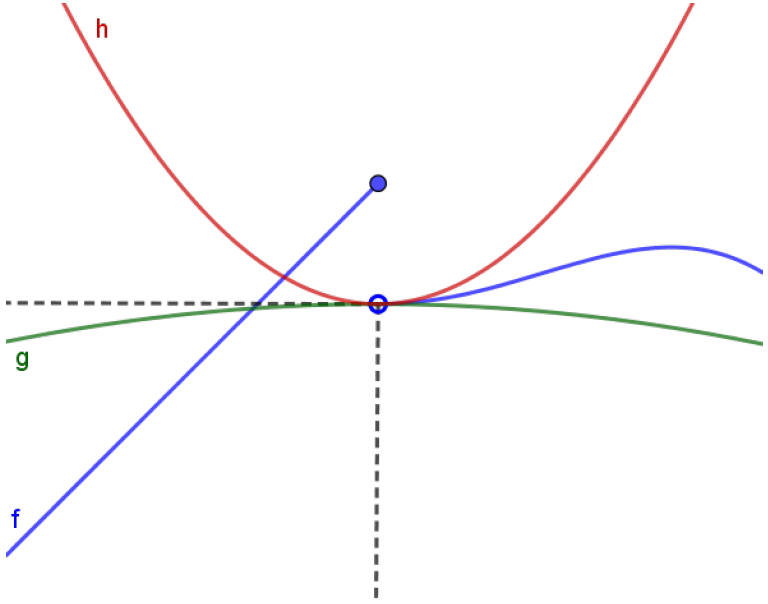
Repare que ainda assim, vale que $\displaystyle \lim_{x\to a^+}f(x) = L$. O que acontece à esquerda de $x=a$ não está sendo discutido nesta versão ``á direita’’ do Teorema.
Podemos ainda extrapolar as conclusões do Teorema do Confronto para o caso de limites no infinito. Vejamos um exemplo antes de enunciarmos mais verões do Teorema.
Calcular o limite $\displaystyle \lim_{x\to +\infty}\frac{2x^3 + 3x^2 - 10x + 2 + \mathrm{sen}(x) }{3x^3-1}$, caso exista.
Inicialmente, veja que temos sempre
\[-1 \leqslant \mathrm{sen}(x) \leqslant 1,\]logo
\[2x^3 + 3x^2 - 10x + 1 \leqslant 2x^3 + 3x^2 - 10x + 2 + \mathrm{sen}(x) \leqslant 2x^3 + 3x^2 - 10x + 3.\]Escolhendo um $x$ suficientemente grande, podemos garantir que $3x^3-1 > 0$. Assim, dividindo as desigualdades acima por $3x^3-1$, temos
\[\frac{2x^3 + 3x^2 - 10x + 1}{3x^3-1} \leqslant \frac{2x^3 + 3x^2 - 10x + 2 + \mathrm{sen}(x)}{3x^3-1} \leqslant \frac{2x^3 + 3x^2 - 10x + 3}{3x^3-1}.\] (Precisamos garantir, de alguma forma, que $3x^3-1 > 0$ pois, do contrário, ao dividir as desigualdades por $3x^3-1 > 0$, o sinal $\leqslant$ poderia se inverter... se lembra?)
Fazendo
\[g(x) = \frac{2x^3 + 3x^2 - 10x + 1}{3x^3-1},\]
\[h(x) = \frac{2x^3 + 3x^2 - 10x + 3}{3x^3-1},\]
temos então
\[g(x) \leqslant f(x) \leqslant h(x)\]para todo $x$ grande o suficiente. Além disso,
\[\lim_{x\to +\infty} g(x) = \lim_{x\to +\infty}\frac{2x^3 + 3x^2 - 10x + 1}{3x^3-1} = \frac{2}{3},\]\[\lim_{x\to +\infty} h(x) = \lim_{x\to +\infty}\frac{2x^3 + 3x^2 - 10x + 3}{3x^3-1} = \frac{2}{3}.\]
Vamos agora esboçar os gráficos de $f$, $g$ e $h$, apenas para tentar ilustrar um pouco a situação. O gráfico de $f$ está em azul, e os gráficos de $g$ e $h$ estão em verde e vermelho, respectivamente.
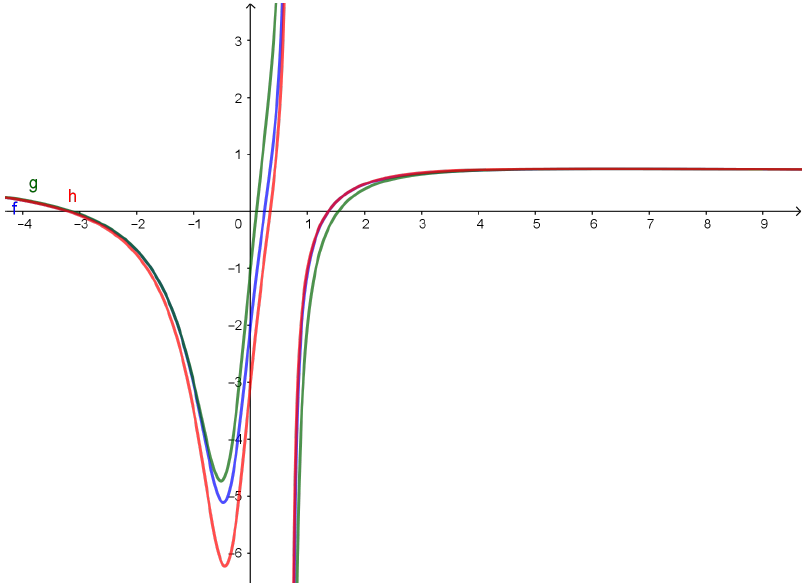
Observe o que acontece se nos concentramos em $x$ positivo e grande o suficiente (com $3x^3-1 > 0$):

Nesta parte observada do esboço, e daqui para $x\to +\infty$, vimos acima que
\[g(x) \leqslant f(x) \leqslant h(x),\]\[\lim_{x\to +\infty} g(x) = \frac{2}{3},\]
\[\lim_{x\to +\infty} h(x) = \frac{2}{3}.\]
É fácil acreditar que o gráfico de $f$ será ``espremido’’ pelos de $g$ e $h$, que estão se aproximando da reta $y=\dfrac{2}{3}$ (a assíntota horizontal). Com isso, teremos claramente
\[\lim_{x\to +\infty} f(x) = \frac{2}{3}.\]
A intuição que utilizamos na solução do exemplo anterior é garantida pelo
Sejam $f$, $g$ e $h$ funções definidas para todo $x > K$, onde $K$ é um número real grande o suficiente. Se
\[g(x) \leqslant f(x) \leqslant h(x)\]para $x > K$, e
\[\lim_{x\to +\infty}g(x) = \lim_{x\to +\infty}h(x) = L,\]então
\[\lim_{x\to +\infty}f(x) = L.\]
Uma versão equivalente pode ser definida para o caso em que $x\to-\infty$:
Sejam $f$, $g$ e $h$ funções definidas para todo $x < K$, onde $K$ é um número real negativo o suficiente. Se
\[g(x) \leqslant f(x) \leqslant h(x)\]para $x < K$, e
\[\lim_{x\to -\infty}g(x) = \lim_{x\to -\infty}h(x) = L,\]então
\[\lim_{x\to -\infty}f(x) = L.\]
Seja $f$ uma função definida em $\mathbb{R}$ tal que, para $x\neq -2$,
\[-x^2 + x + 2\leqslant f(x) \leqslant \dfrac{x^2-4}{x+2}.\]Calcule $\displaystyle \lim_{x \to -2} f(x)$, se existir. Solução: Temos
\[\lim_{x\to-2} -x^2 + x + 2 = -(-2)^2 + (-2) + 2 = -4\]e
\[\lim_{x\to-2} \frac{x^2-4}{x+2} = \lim_{x\to-2} \frac{(x-2)(x+2)}{x+2} = \lim_{x\to-2} (x-2) = -4.\]Assim, como $-x^2 + x + 2\leqslant f(x) \leqslant \dfrac{x^2-4}{x+2}$, temos pelo Teorema do Confronto,
\[\lim_{x\to-2} f(x) = -4.\]

