Continuidade
.
Vimos no estudo sobre limites que o limite de algumas funções quando $x$ tende a $a$ coincide com a imagem da função no ponto $a$. Funções com esta propriedade são ditas contínuas em $a$. A ideia matemática de continuidade é a da própria palavra, ou seja, de um processo contínuo, sem quebras, que não possui mudanças abruptas.
Quando pensamos, por exemplo, em um valor aproximado para $\sqrt{3,9}$, logo vem à mente o valor $2$, afinal, $3,9$ está próximo de 4! Isso é verdade, pois a função raiz quadrada é contínua em seu domínio, se não o fosse, seu valor em $3,9$ poderia estar bem ``longe'' de 2!
Considere a função definida por
\[f(x)=\begin{cases} x^2+1,&\text{se } x \leqslant 0\\x^3,&\text{se } x > 0. \end{cases} \]Como $\displaystyle\lim_{x\to 0^-}f(x) = \lim_{x\to 0^-}(x^2+1)=1 $ e $\displaystyle\lim_{x\to 0^+}f(x) = \lim_{x\to 0^+}x^3 = 0$, o limite $\displaystyle\lim_{x\to 0}f(x)$ não existe. No gráfico da $f$, ao lado, isto representa que há um ``salto'' ou uma ``quebra'' no ponto $x=0$.
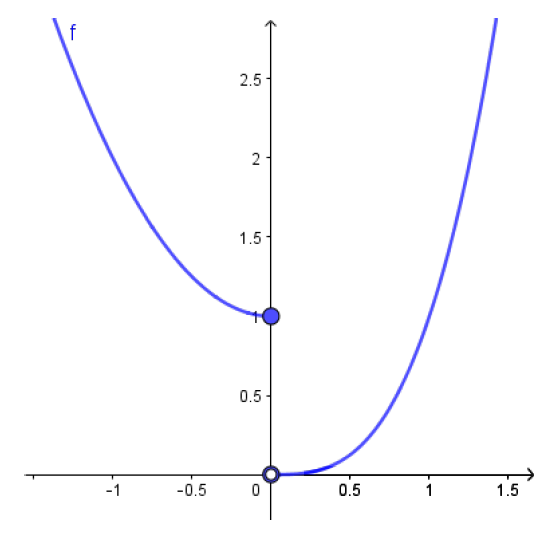
Considere a função definida por
\[f(x)=\begin{cases} |x|,&\text{se } x \neq 1\\0,&\text{se } x = 1. \end{cases} \]Sabemos que $\displaystyle\lim_{x\to 1}f(x) = \lim_{x\to 1}|x|=1 $. Entretanto, como
$f(1)=0$, temos que $\displaystyle\lim_{x\to 1}f(x)\neq f(1)$. No gráfico da $f$, ao lado, isto representa que há um ``salto'' ou uma ``quebra'' no ponto $x=1$.
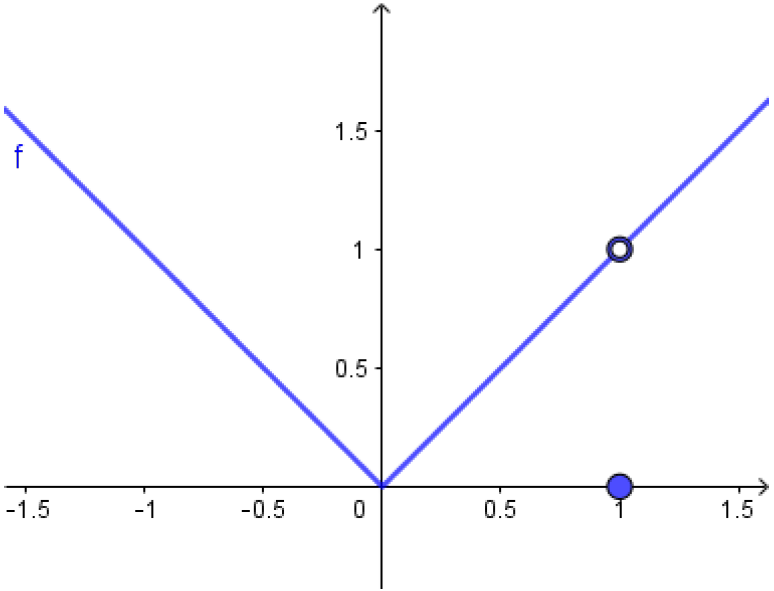
Definição de Continuidade
(Função contínua) Uma função $f:X\rightarrow \mathbb{R}$ é contínua em $a\in X$ se $\displaystyle\lim_{x\to a} f(x)=f(a)$.
Observe que na definição de continuidade há três aspectos envolvidos:
$f(a)$ está definido, isto é, o ponto $a$ está no domínio da função
o limite da função em $a$ existe
e o limite coincide com o valor que a função assume em $x=a$, isto é, $\displaystyle \lim_{x\to a}f(x) = f(a)$.
Diremos que $f:X\rightarrow \mathbb{R}$ é descontínua em $a\in X$ se $f$ não for contínua em $a$, isso ocorre por dois motivos: o limite da função no ponto $x=a$ não existe ou ele existe, mas é diferente de $f(a)$. Diremos ainda que $f$ é contínua em um conjunto $A \subset X$ se $f$ for contínua em todo ponto $a \in A$.
No Exemplo 1, a função $f$ é descontínua em $0$ e contínua em $\mathbb{R}-\{0\}$. De fato, para todo $a \neq 0$, teremos $\displaystyle \lim_{x\to a}f(x) = \lim_{x\to a}(x^2+1)=a^2+1 = f(a)$ se $a < 0$ e $\displaystyle \lim_{x\to a}f(x) = \lim_{x\to a}x^3=a^3 = f(a)$ se $a > 0$.
No Exemplo 2, a função $f$ é descontínua em $1$ e contínua em $\mathbb{R}-\{1\}$. De fato, para todo $a \neq 1$, teremos $\displaystyle \lim_{x\to a}f(x) = \lim_{x\to a}|x|=|a|=f(a)$.
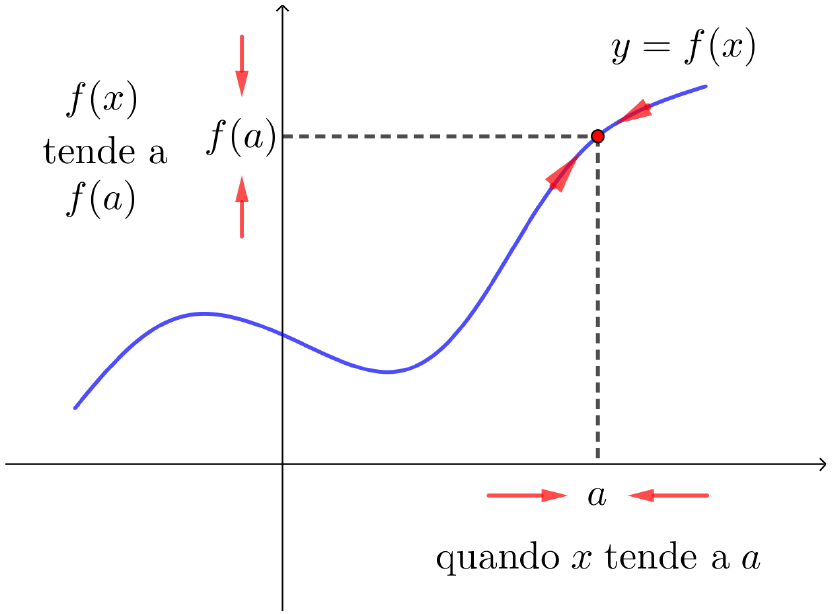 | Se $f$ é contínua em $a$, então $f(x)$ está próximo de $f(a)$, se $x$ estiver suficientemente próximo de $a$. Isto é, $f(x)$ tende a $f(a)$ quando $x$ tende a $a$. Geometricamente, o gráfico de uma função contínua em um ponto $a$ não possui quebra em $a$. Quando uma função é contínua em um intervalo, seu gráfico pode ser traçado sem nenhuma quebra, isto é, ``sem tirar o lápis do papel''. |
Se $f$ é contínua em $a$, então $f(x)$ está próximo de $f(a)$, se $x$ estiver suficientemente próximo de $a$. Isto é, $f(x)$ tende a $f(a)$ quando $x$ tende a $a$. Geometricamente, o gráfico de uma função contínua em um ponto $a$ não possui quebra em $a$. Quando uma função é contínua em um intervalo, seu gráfico pode ser traçado sem nenhuma quebra, isto é, ``sem tirar o lápis do papel''.
Pensando nos gráficos das funções trigonométricas, vemos que $y=\cos(x)$ e $y=\mathrm{sen}(x)$ são contínuas em todo ponto de $\mathbb{R}$, já $y=\tan(x)$ e $y=\sec(x)$ são contínuas em todo ponto de seus domínios, ou seja, para $x\neq \frac{\pi}{2} +k\pi$ e $y=\mathrm{cotg}(x)$ e $y=\mathrm{cossec}(x)$ são contínuas em $x\neq k\pi$. Outros exemplos de funções contínuas em todos os pontos de seus domínios são função modular, exponencial, logaritmo, raízes, polinômios e funções racionais.
Observação: Há uma pequena variação na forma como alguns autores definem e trabalham com o conceito de descontinuidade. Lembre-se de que nós definimos, alguns parágrafos acima, que a função ``$f :X\rightarrow \mathbb{R}$ é descontínua em $a\in X$ se $f$ não for contínua em $a$'', isto é, só definimos descontinuidade em pontos do domínio da função. Assim, por exemplo, com a nossa definição, não faz sentido falar que (e nem perguntar se) $f(x)=\dfrac{1}{x-1}$ ou $f(x)=\dfrac{x^2-1}{x-1}$ são contínuas ou descontínuas em $x=1$, pelo simples fato de que $x=1$ não pertence ao domínio destas funções, que é $\mathbb{R}-\{1\}$ em ambos os casos. Alguns autores, porém, definiriam que estas funções são descontínuas em $x=1$; no caso de $f(x)=\dfrac{1}{x-1}$, diriam ter uma descontinuidade infinita e, no caso de $f(x)=\dfrac{x^2-1}{x-1}$, uma descontinuidade removível.
Vamos verificar a continuidade da função abaixo em $x=1$.
$$f(x)= \begin{cases} \dfrac{x^2-1}{x-1}, & \text{se } x < 1. \\\cos(x-1)+1, & \text{se } x \geq1 . \end{cases} $$Vamos então ver, pela definição, se $f$ é contínua em $x=1$:
\[\displaystyle\lim_{x\to 1^-}f(x)= \displaystyle\lim_{x\to 1^-} \dfrac{x^2-1}{x-1}= \lim_{x\to 1^-} \dfrac{(x-1)(x+1)}{x-1}= \lim_{x\to 1^-}x+1=2,\] \[\lim_{x\to 1^+}f(x)= \lim_{x\to 1^+} \left(\cos(x-1)+1\right) = \cos(1-1)+1 = 2,\] \[f(1) = \cos(1-1)+1 = 2\]Assim, como $\displaystyle\lim_{x\to 1^-}f(x) = \displaystyle\lim_{x\to 1^+}f(x) = f(1)$, temos que o limite de $f$ existe em $x=1$ e este limite é igual a $f(1)$. Com isso, $f$ é contínua em $x=1$.
Vamos verificar a continuidade da função abaixo em $x=2$.
$$f(x)= \begin{cases} \dfrac{x^3-2x^2-x+2}{x-2}, & \text{se } x < 2. \\\sec(x-2)+1, & \text{se } 2 \leq x <2+\pi/2 . \end{cases} $$Vejamos os limites laterais em $x=2$:
Como os limites laterais são distintos, não existe o limite da $f$ quando $x$ tende a $2$, portanto a $f$ não pode ser contínua em $x=2$.
Vamos verificar a continuidade da função abaixo em $x=0$ e $x=1$.
$$f(x)= \begin{cases} \mathrm{sen}\left(\frac{1}{x}\right) , & \text{se } x < 0. \\5 , & \text{se } 0\leq x \leq1 . \\\dfrac{x}{1-x}, & \text{se } x > 1 . \end{cases} $$Vejamos primeiro os limites laterais quando $x$ tende a $0$:
mas esse limite não existe, pois o valor do seno fica oscilando entre -1 e 1 indefinidamente. Portanto, podemos afirmar que a $f$ não é contínua em $x=0$.
Analisando agora quando $x$ tende a $1$:
logo a $f$ também não pode ser contínua em $x=1$, pois o limite não existe.
Vamos verificar se existe algum valor de $b$, tal que a função abaixo seja contínua em $x=0$.
\[f(x)= \begin{cases} \dfrac{e^x+1}{x^2+1}, & \text{se } x < 0. \\b , & \text{se } x=0. \\ 2+ x^3 \,\mathrm{sen}\left(\dfrac{1}{x}\right), & \text{se } x > 0 . \end{cases} \]Temos
\[\displaystyle\lim_{x\to 0^-} f(x) = \displaystyle\lim_{x\to 0^-} \dfrac{e^x+1}{x^2+1} = \frac{e^0+1}{1}=2,\] \[\displaystyle\lim_{x\to 0^+} f(x) =\displaystyle\lim_{x\to 0^+} 2+ x^3 \,\mathrm{sen}\left(\dfrac{1}{x}\right) = 2+ 0=2,\]pois pelo Teorema do Anulamento $\displaystyle\lim_{x\to 0}x^3 \, \mathrm{sen}\left(\dfrac{1}{x}\right)=0$.
\[f(0) = b\]logo, para que $\displaystyle\lim_{x\to 0^-} f(x) = \lim_{x\to 0^+} f(x) = f(0)$, precisamos ter $b = 2$.
Verificar se existe algum valor de $b$, tal que a função abaixo seja contínua em $x=0$.
\[f(x)= \begin{cases} \dfrac{\mathrm{sen}(|x|)}{x}, & \text{se } x < 0 \\b , & \text{se } x=0 \\\ln(x+e), & \text{se } x > 0 . \end{cases} \]Temos
\[\displaystyle\lim_{x\to 0^-} f(x) = \displaystyle\lim_{x\to 0^-} \dfrac{\mathrm{sen}(|x|)}{x} \underset{x<0}{=} \displaystyle\lim_{x\to 0^-}\dfrac{\mathrm{sen}(-x)}{x}\underset{\substack{\text{o seno}\\\text{é}\\\text{ímpar}} }{=}\displaystyle\lim_{x\to 0^-}\dfrac{-\mathrm{sen}(x)}{x}=-1,\] \[\displaystyle\lim_{x\to 0^+} f(x) =\displaystyle\lim_{x\to 0^+} \ln(x+e)=\ln(e)=1.\]Como os limites laterais são diferentes, não existe $\displaystyle\lim_{x\to 0} f(x)$. Assim, não existe nenhum valor real para $b$ que torne a $f$ contínua em $x=0$.
Dizemos que a $f$ é contínua no intervalo fechado $[a,b]$, quando o for em $(a,b)$ e além disso $\displaystyle\lim_{x\to a^+}f(x)=f(a)$ (continuidade à direita em $a$) e $\displaystyle\lim_{x\to b^-}f(x)=f(b)$ (continuidade à esquerda em $b$).
Observação: $f(x)$ é contínua em $x=a$, quando para todo $\epsilon>0$ dado, existir $\delta>0$, tal que, se $|x-a|<\delta$, então $|f(x)-f(a)|<\epsilon$. Esta é a definição formal de continuidade, decorrente da definição formal de limite.
Dadas duas funções, $f$ e $g$, contínuas em $a$:
- A função soma $f(x) + g(x)$ é contínua em $a$. (A soma de funções contínuas é contínua.)
- A função diferença $f(x) - g(x)$ é contínua em $a$. (A diferença de funções contínuas é contínua.)
- A função produto $c\,f(x)$ é contínua em $a$, para todo $c \in\mathbb{R}$. (O produto de uma função contínua por uma constante é contínua.)
- A função produto $f(x)\cdot g(x)$ é contínua em $a$. (O produto de funções contínuas é contínua.)
- Se $g(a) \neq 0$, $\dfrac{f(x)}{g(x)}$ é contínua em $a$. (O quociente de funções contínuas é contínua, desde que o denominador não se anule.)
Esse resultado é bem conhecido. Sua demonstração decorre das propriedades análogas de limite.
A função $f(x)=\dfrac{\mathrm{sen}(x)}{x^4+1}$ é contínua em $\mathbb{R}$, pois $\mathrm{sen}(x)$ e $x^4+1$ são contínuas em $\mathbb{R}$ e $x^4+1 \neq 0$ para todo $x \in \mathbb{R}$. Portanto, pelo Teorema 1, o quociente será uma função contínua em $\mathbb{R}$.
A função $f(x)=\dfrac{|x|\,\cos(x)}{1-x^2}$ é contínua em $\mathbb{R}-\{-1,1\}$. De fato, $|x|$ e $\cos(x)$ são contínuas em $\mathbb{R}$, logo pelo Teorema 1, $|x|\,\cos(x)$ também é. Além disso, $1-x^2$ é contínua em $\mathbb{R}$ e $x^2-1 \neq 0$ para todo $x \in \mathbb{R}-\{-1,1\}$, portanto o quociente será uma função contínua em $\mathbb{R}-\{-1,1\}$.
Determinar os valores de $a$ e $b$ reais para que a função $f$ definida abaixo seja contínua em $\mathbb{R}$:
\[f(x)= \begin{cases} \dfrac{\mathrm{sen}(x)}{|x|}, & \text{se } x < 0 \\ax+b, & \text{se } 0\leq x \leq 1 \\\ln(x), & \text{se } x > 1 . \end{cases} \]Para $x<0$, $f(x) = \dfrac{\mathrm{sen}(x)}{|x|}$ é contínua. O mesmo acontece para $x>1$, onde $f(x) = \ln(x)$ e para $0 < x < 1$, onde $f(x)$ é a função afim $ax+b$, que é contínua independentemente do valor dos parâmetros $a$ e $b$.
Assim, para que $f$ seja contínua em $\mathbb{R}$, só falta garantir que seja contínua em $0$ e $1$, ou seja, que $\displaystyle\lim_{x\to 0}f(x) = f(0)$ e $\displaystyle\lim_{x\to 1}f(x) = f(1)$.
\[\lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} \frac{\mathrm{sen}(x)}{|x|} \underset{x<0}{=} \lim_{x\to 0^-} \frac{\mathrm{sen}(x)}{-x} = -\lim_{x\to 0^-} \frac{\mathrm{sen}(x)}{x}=-1.\]Assim, teremos $\displaystyle\lim_{x\to 0^+} f(x)= a\cdot 0 + b = f(0) = \displaystyle\lim_{x\to 0^-} f(x) = -1$, logo $b = -1$. Por outro lado,
\[\displaystyle\lim_{x\to 1^+} f(x) = \displaystyle\lim_{x\to 1^+} \ln(x) = \ln(1) = 0.\]Assim, teremos $\displaystyle\lim_{x\to 1^-} f(x)= a\cdot 1 + b \underset{b=-1}{=} a - 1 = f(1) = \displaystyle\lim_{x\to 1^+} f(x) = 0$, logo $a-1 = 0$, e então $a=1$.
Note que, como $f(x)$ é polinomial para $0 \leq x \leq 1$, temos também $\displaystyle\lim_{x\to 0^+} f(x) = f(0)$ e $\displaystyle\lim_{x\to 1^-} f(x) = f(1)$.
O próximo Teorema nos diz que ``composta de funções contínuas é contínua''.
Se $g$ é contínua em $x=a$ e $f$ é contínua em $x=g(a)$, então a função $f\circ g$, dada por $(f\circ g)(x) = f(g(x))$ é contínua em $x=a$.
A função definida por $h(x) = \mathrm{sen}(x^2)$ é contínua em $\mathbb{R}$, pois $g(x) = x^2$ e $f(x)=\mathrm{sen}(x)$ são contínuas em $\mathbb{R}$.
A função definida por $F(x) = \ln(1+\cos(x))$ é contínua em $\mathbb{R} - \{\pi+2k\pi, k\in\mathbb{Z}\}$. Sabemos que $f(x) = \ln(x)$ é contínua em seu domínio $(0,+\infty)$ e $g(x)=1+\cos(x)$ é contínua em $\mathbb{R}$, com isso, $f(g(x))$ será contínua sempre que $g(x)$ pertencer ao domínio de $f$, isto é, sempre que $g(x) > 0$. Como $\cos(x) \geqslant -1$, $g(x)$ só estará fora de $(0,+\infty)$, que é o domínio de $f$, quando $1+\cos(x)=0$, logo $\cos(x)= -1$, ou seja, $x=\pi+2k\pi, k \in \mathbb{Z}$. Assim, o domínio de $F=f\circ g$ é $\mathbb{R} - \{\pi+2k\pi, k\in\mathbb{Z}\}$.

