Teorema do Valor Intermediário
O Teorema do Valor Intermediário é um dos resultados centrais relativos à continuidade. Apesar de suas muitas aplicações e da profundidade de sua conclusão, sua afirmação é bastante intuitiva e tão fácil de entender quanto de acreditar.
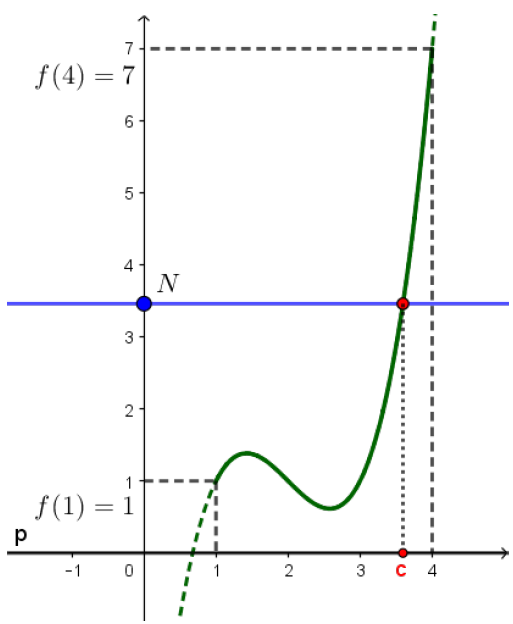
Se $f$ é uma função contínua no intervalo $[a,b]$, o gráfico da função é desenhado com um único traço unindo os pontos $(a,f(a))$ e $(b,f(b))$. Vamos supor que $f(a) < f(b)$, como na figura ao lado.
Considere então qualquer reta horizontal que passe entre os pontos $(a,f(a))$ e $(b,f(b))$, isto é, qualquer reta $y=N$, com $f(a) < N < f(b)$. Esta reta deverá, obviamente, cortar o gráfico da função, pois, como $f$ é contínua no intervalo, seu gráfico não pode saltar de um lado para outro da reta, sem passar por ela. Assim, existirá algum $c \in (a,b)$ tal que $f(c) = N$.
Obviamente, o resultado continua valendo se $f(a) > f(b).$
A existência deste $c$, tal que $f(c) = N$, dada que a função seja contínua, é o que garante o Teorema do Valor Intermediário (TVI), que enunciaremos a seguir.
(Teorema do Valor Intermediário) Suponha que $f$ seja contínua em um intervalo fechado $[a,b]$ e seja $N$ um número qualquer entre $f(a)$ e $f(b)$. Então, existe $c \in (a,b)$, tal que $f(c) = N$.
Uma conclusão natural deste resultado, é que, com $x$ variando no intervalo $(a,b)$, uma função contínua assume todos os valores entre $f(a)$ e $f(b)$.
Considerando a função definida por $f(x)=x^3-7x^2+16x-11$, existe algum $c \in (1,4)$, tal que $f(c) = 1$?
Sim, pois a $f$ é contínua no intervalo fechado $[1,4]$, $f(1) = -1$, $f(4)=5$ e $-1 < 1 < 5$, logo o TVI garante que exista tal $c$. Observe que o TVI não nos diz como encontrar o valor de $c$ (por curiosidade, existem dois valores, $c=2$ e $c=3$).
Considerando a função definida por $f(x) = \dfrac{1}{x^2+1}$, existe $c \in (0,+\infty)$, tal que $f(c) = \dfrac{1}{\pi}$?
O TVI não foi enunciado para intervalos ilimitados, como este, portanto não podemos utilizá-lo diretamente, o que não quer dizer que ele não será útil. Como $\displaystyle \lim_{x\to+\infty} \dfrac{1}{x^2+1} = 0$, pela definição de limite com $x\to+\infty$, existe $k > 0$ tal que $f(k) < \dfrac{1}{\pi}$ (se o valor de $f$ se aproxima de 0 quando $x\to+\infty$, ele obviamente terá que ser menor que $\dfrac{1}{\pi}$ em algum valor de $x$). Assim, temos $ f(k)< \dfrac{1}{\pi}<f(0)=1$ e, como $f$ é contínua em $[0,k]$, existe $c \in (0,k)$, tal que $f(c) = \dfrac{1}{\pi}$.
Todo polinômio de grau ímpar possui pelo menos uma raiz real. Seja $p(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x+a_0$, com $n$ ímpar e $a_n \neq 0$. Suponha inicialmente que $a_n > 0$ e, neste caso, teremos $\displaystyle\lim_{x\to+\infty} p(x) = +\infty$ e $\displaystyle\lim_{x\to-\infty} p(x) = -\infty$. Assim, existem $a < 0$ e $b>0$ tais que $p(a) < 0 < p(b)$ e, como $p$ é uma função contínua em $[a,b]$, o TVI nos garante que existe $c \in (a,b)$, tal que $p(c) = 0$. Se, por outro lado, tivéssemos $a_n < 0$, então $\displaystyle\lim_{x\to+\infty} p(x) = -\infty$ e $\displaystyle\lim_{x\to-\infty} p(x) = +\infty$ e poderíamos tomar $a < 0, b> 0$ tais que $p(a) > 0 > p(b)$, e o resultado seguiria da mesma forma.
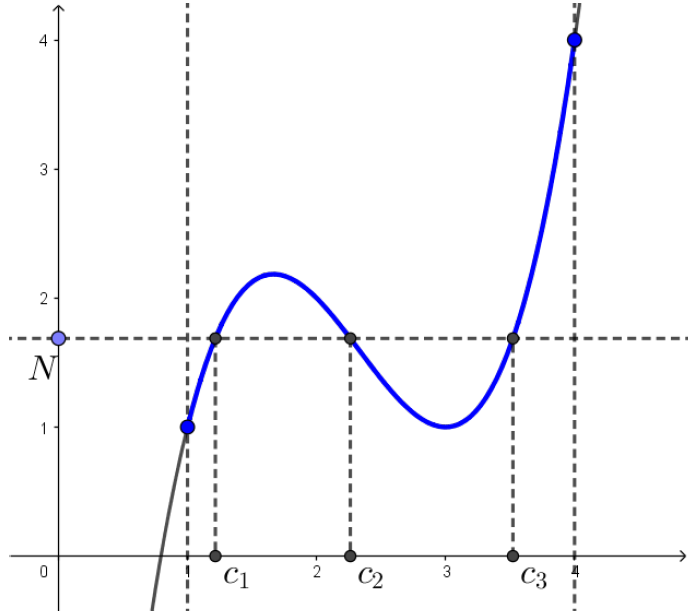
Observação: Como visto no Exemplo 1, na conclusão do Teorema do Valor Intermediário, pode existir mais de um valor para $c$ tal que $f(c)=N$. No exemplo abaixo, podemos ver que, existem três valores distintos $c_1$, $c_2$ e $c_3$ no intervalo $(a,b)$ tais que $f(c_1)=f(c_2)=f(c_3) = N$.
Este exemplo mostra que a conclusão do Teorema do Valor Intermediário não é válida, em geral, para funções descontínuas. Consideremos a função $f:[0,1]\rightarrow\mathbb{R}$, definida por $f(x)=0$ se $0\leq x<\frac{1}{2}$ e $f(x)=1$ se $\frac{1}{2}\leq x\leq 1$.
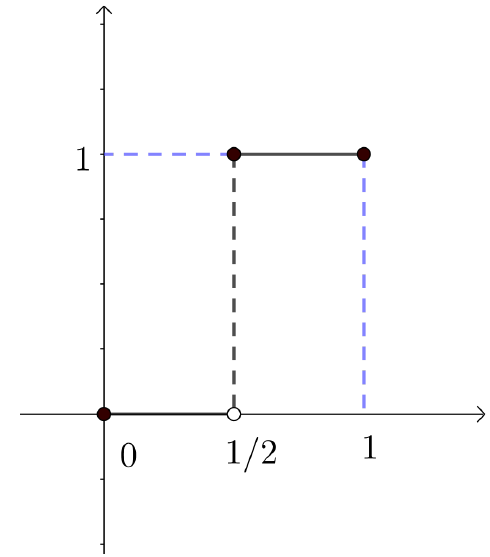
A função $f$ não é contínua em $[0,1]$ já que não é contínua em $\frac{1}{2}$. Se tomarmos qualquer número real $N$, com $f(0)=0<N<1=f(1)$, não é possível encontrar $x\in(0,1)$ com $f(x)=N$. Isto significa que a conclusão do TVI não é válida para a função $f$. Isto, obviamente, não indica que o teorema não escteja correto, mas sim que esta função não satisfaz suas hipóteses ($f$ não é contínua em $[a,b]$).
Observe que bastou um único ponto de descontinuidade em $[0, 1]$ para o TVI não poder ser aplicado à função $f$.
Existência de raízes de equações
O TVI é muito utilizado para garantir a existência de raízes de equações, e até mesmo para dar uma estimativa destas raízes, quando a equação pode ser escrita na forma $f(x) = c$. Vejamos alguns exemplos.
Mostrar que a equação $4x^3-6x^2+3x-2 = 0$ tem uma raiz no intervalo $(1,2)$.
A equação pode ser escrita como $f(x)=0$, onde $f(x) = 4x^3-6x^2+3x-2$. Note que, por ser uma função polinomial, $f$ é contínua em $[1,2]$.
Temos $f(1)=4-6+3-2 = -1 < 0$ e $f(2)=32-24+6-2=12 >0$. Assim, $f(1) < 0 < f(2)$, logo $N = 0$ é um número entre $f(1)$ e $f(2)$. Como $f$ é contínua, o TVI nos garante que existe $c \in (1,2)$, tal que $f(c) = 0$, o que implica que $4x^3-6x^2+3x-2 = 0$ tem pelo menos uma raiz em $(1,2)$.
Provar que existe $x\in\mathbb{R}$, tal que $x = \cos^3(x) + \mathrm{sen}^3(x)$.
Seja $f(x) = x - \cos^3(x) - \mathrm{sen}^3(x)$. Note que $f(x) = 0$ se, e somente se, $x = \cos^3(x) + \mathrm{sen}^3(x)$, assim, buscar uma raiz para a equação é equivalente a encontrar $x$ tal que $f(x)=0$.
Temos $f(0) = 0 - \cos^3(0) - \mathrm{sen}^3(0) = -1$ e $f\left(\frac{\pi}{2}\right) = \frac{\pi}{2} - \cos^3\left(\frac{\pi}{2}\right)-\mathrm{sen}^3\left(\frac{\pi}{2}\right) = \frac{\pi}{2} - 0^3 - 1^3 = \frac{\pi}{2} - 1 > 0$, pois $\pi > 2$. Assim, $f(0) < 0 < f\left(\frac{\pi}{2}\right)$ e, como $f$ é contínua em $\left[0,\dfrac{\pi}{2}\right]$, existe $x \in \left(0,\dfrac{\pi}{2}\right)$ tal que $f(x)=0$, logo $x = \cos^3(x) + \mathrm{sen}^3(x)$.
Localize uma raiz de $f(x)=\sqrt{x^3+1}-2x$ em um intervalo de comprimento 1.
Observe que $f(0)=1>0$ e $f(1)=\sqrt{2}-2<0$. Como a $f$ é contínua em $[0,1]$, pois $\sqrt{x^3+1}$ é composta de contínuas e $2x$ também é contínua, o TVI nos diz que, existe $c\in(0,1)$, tal que $f(c)=0$. Portanto, $x=c$ é uma raiz da função $f$.
Mostre que os gráficos de $f(x)=x^3-x^2$ e $g(x)=x+1$ possuem um ponto de interseção no intervalo $[1,2]$.
Precisamos mostrar que $f(x)=g(x)$ para algum $x\in[1,2]$, mas esse fato equivale a mostrar que $f(x)-g(x)=0$ para algum $x\in[1,2]$. Definimos $h(x)=f(x)-g(x)$, para $x\in[1,2]$. Observe que $h$ é contínua em $[1,2]$, $h(1)=-2<0$ e $h(2)=2^3-2^2-2-1=1>0$, portanto pelo TVI, existe $c\in(1,2)$, tal que $h(c)=0$, ou seja, $f(c)=g(c)$.

