Expressões do Primeiro Grau

Abaixo, vamos descrever uma situação do dia-a-dia.

Você pode visualizar como o preço $y$ da corrida varia em função da quantidade de quilômetros percorridos no applet abaixo:

Expressões como a do valor da corrida acima são chamadas expressões do primeiro grau.

A expressão $y=bx+c$

Uma expressão do primeiro grau é do tipo

\begin{eqnarray}\tag{1}y=bx+c,\end{eqnarray}

com \(x \in \mathbb{R}\), onde $b$ e $c$ são constantes reais, com $b\not = 0$. $b$ e $c$ são ditos, respectivamente, coeficientes angular e linear.

Dados dois pontos $P_1=(x_1,y_1)$ e $P_2=(x_2,y_2)$ que satisfazem a expressão (1), temos que,

\[y_1=bx_1+c \text{ e } y_2=bx_2+c,\]

de modo que,

\[y_1-y_2=bx_1+c-(bx_2+c)=bx_1-bx_2=b(x_1-x_2).\]

Portanto, se definirmos $\Delta y$ como $\Delta y=y_1-y_2$ e $\Delta x$ como $\Delta x=x_1-x_2$, segue que,

\begin{equation}\tag{2}\Delta y=b\;\Delta x,\end{equation}

de forma que,

\begin{equation}\tag{3}\dfrac{\Delta y}{\Delta x}=b.\end{equation}

Observe que:

• (3) significa que a taxa de variação média de $y$ em relação a $x$ é constante e igual a $b$.

• (2) nos diz que quando $x$ varia de uma quantidade $\Delta x$, $y$ sofre uma variação $\Delta y=b\;\Delta x$. Por exemplo, se tomarmos $b=4$ e $x$ sofrer um acréscimo de $0.1$, então $y$ sofrerá um acréscimo de $4\times 0.1=0.4$. Já se tivermos $b=-2$ e $x$ sofrer um acréscimo de $0.1$, então $y$ sofrerá uma variação de $-2\times 0.1=-0.2$, ou seja, sofrerá um decréscimo de $0.2$.

Retas

A representação de $y=bx+c$, \(x \in\mathbb{R}\), no plano cartesiano, dada pelos pares ordenados $(x,y)$ da forma $(x,bx+c)$ é uma reta não-vertical.

• Quando $b=0$, temos a equação $y=c$, que é a equação de uma reta horizontal, ou seja, uma reta paralela ao eixo $y$. Neste caso, observa-se que para cada valor de $x$, o $y$ associado é o mesmo, formando pontos da forma $(x,c)$.
  

  

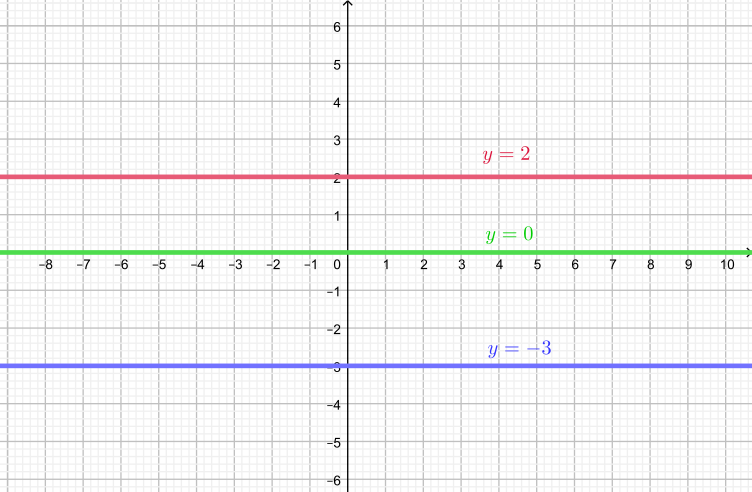
• Se $b>0$, então a medida que aumentamos $x$, isto é, variando de $x_1$ para $x_2$, onde $x_1 < x_2$, vimos anteriormente que a reta $y=bx+c$ é crescente e ``corta'' o eixo $x$ na raiz \(x=-\dfrac{c}{b}\). Portanto, a reta $y=bx+c$ estará acima do eixo $x$ após a raiz e estará abaixo do eixo $x$ antes da raiz. Estar acima do eixo $x$, significa que a ordenada $y$ do ponto da reta $(x,y)=(x, bx+c)$ é positiva e, da mesma forma, estar abaixo do eixo $x$, significa que a ordenada $y$ do ponto da reta $(x,y)=(x, bx+c)$ é negativa. Temos assim, que

  \[y=bx+c>0 \Leftrightarrow x>-\dfrac{c}{b};\]
  \[y=bx+c<0 \Leftrightarrow x<-\dfrac{c}{b} \text{ e }\]
  \[y=bx+c=0 \Leftrightarrow x=-\dfrac{c}{b}.\]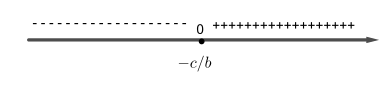

  

• Se $b<0$, vimos anteriormente que a reta $y=bx+c$ é decrescente e ``corta'' o eixo $x$ na raiz \(x=-\dfrac{c}{b}\). Portanto, a reta $y=bx+c$ estará acima do eixo $x$ antes da raiz e estará abaixo do eixo $x$ após raiz. Portanto a ordenada $y$ do ponto da reta $(x,y)=(x, bx+c)$ é positiva antes da raiz e negativa após a raiz. Temos assim, que

  \[y=bx+c>0 \Leftrightarrow x<-\dfrac{c}{b};\]
  \[y=bx+c<0 \Leftrightarrow x>-\dfrac{c}{b} \text{ e }\]
  \[y=bx+c=0 \Leftrightarrow x=-\dfrac{c}{b}.\]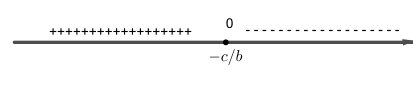

  

Observe o sinal da expressão \(y=\dfrac{x}{2} + 1\) da segunda figura da página 4 (em verde).

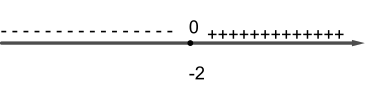
Note, no gráfico, que $y>0$ corresponde à parte do gráfico acima do eixo $x$ e que $y<0$ corresponde à parte do gráfico abaixo do eixo $x$.

Repare o sinal da expressão $y=-2x + 4$ da terceira figura da página 2 (em vermelho).

De posse dos conhecimentos adquidos anteriormente, vamos resolver o problema do exemplo inicial e determinar em que meses ela estará juntando dinheiro para a viagem?

Observe que após $x$ meses, a pessoa terá economizado $500+180x$. Assim terá juntado o dinheiro para o celular quando

$$500+180x-2480=0.$$

Portanto, ela passará a economizar para a viagem quando

$$500+180x-2480 >0.$$

Sendo assim, o problema se resume ao estudo do sinal da expressão.

$$y=500+180x-2480=180x-1980.$$

Como estamos diante de uma expressão do primeiro grau, nosso primeiro passo é encontrar a raiz da equação $180x-1980=0$. Neste caso, temos $180x-1980=0 \Leftrightarrow x=11$. O segundo passo é verificar o sinal do coeficiente $b$ do termo de primeiro grau. Como $b=180>0$, a reta associada à expressão $y=180x-1980$ é crescente e, portanto, $y=180x-1980$ é positivo depois da raiz e negativo, antes. Ou seja, temos que. \(y=180x-1980>0 \Leftrightarrow x>11;\) \(y=180x-1980<0 \Leftrightarrow x<11 \text{ e }\) \(y=180x-1980=0 \Leftrightarrow x=11.\) Logo, em 11 meses terá o dinheiro para o celular e a partir de 11 meses, ou seja, do décimo segundo mês em diante,ela já estará economizando para a viagem.

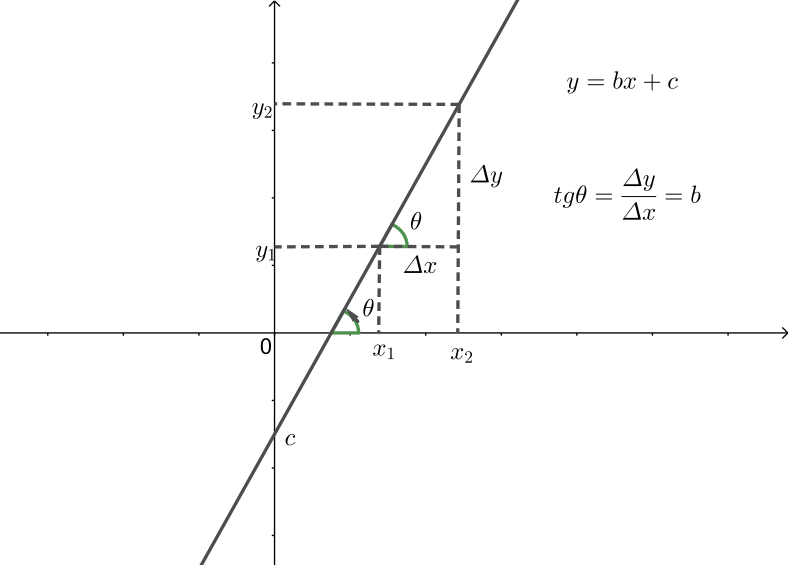
Coeficiente Angular $\times$ Tangente

Dada a expressão $y=bx+c$, lembre-se que na expressão (3), vimos que

\[b=\dfrac{\Delta y}{\Delta x}.\]

Conforme você pode ver na figura abaixo, o coeficiente angular $b$ é igual à tangente do ângulo que a reta faz com o eixo $x$, marcando o ângulo a partir do semieixo positivo dos $x$ até a reta, no sentido anti-horário.

Por esta razão, o coeficiente $b$ é dito a inclinação da reta de equação $y=bx+c$.

Observações:

1. Reta vertical: uma reta vertical é descrita da forma $x=k$, \(k\in \mathbb{R}\). Neste caso, o ângulo formado é de $90^\circ$ e não existe tangente desse ângulo. Mas, observe que esta reta não pode ser colocada na forma $y=bx+c$ que é a expressão com a qual estamos trabalhando.

2. Reta horizontal: uma reta horizontal é descrita da forma $y=c$. Sendo horizontal, o ângulo formado é de $0^\circ$ e, de fato, $b=0=\tan(0^\circ)$.

3. Retas paralelas possuem o mesmo coeficiente angular.

4. Conhecendo o coeficiente angular $b$ de uma reta e um ponto $(x_0,y_0)$ pertencente à reta, podemos determinar sua equação, a saber:

   \begin{eqnarray}\tag{4}y=b(x-x_0)+y_0.\end{eqnarray}

   De fato, se $(x_0,y_0)$ é uma ponto da reta $y=bx+c$, isto significa que este ponto satisfaz esta equação e, portanto, temos que $y_0=bx_0+c$. Desta forma, segue que

   \begin{eqnarray*}y_0=bx_0+c \Leftrightarrow c=y_0-bx_0.\end{eqnarray*}

   Substituindo o resultado acima na equação da reta, temos que

   \begin{eqnarray*}y=bx+c \Rightarrow y=bx+y_0-bx_0= b(x-x_0)+y_0.\end{eqnarray*}

   Esse fato será muito importante ao longo da disciplina! Guarde no coração!

5. Dados dois pontos sobre uma reta, podemos calcular o coeficiente angular $b$ da reta através da equação $b=\dfrac{\Delta y}{\Delta x}$ e, escolhendo um dos pontos, somos capazes de escrever a equação da reta utilizando a equação (4).