Derivadas das Funções Elementares e Regras de Derivação (soma, produto e quociente)
Estudamos anteriormente a definição de derivada. O cálculo de derivadas nem sempre é feito pela definição: para um conjunto considerável de funções existem regras e tabelas que facilitam. Essa seção e a próxima tratam exatamente dessa possibilidade.
Nessa seção enunciamos os resultados formalmente, mas nem todas as demonstrações serão apresentadas. Elas podem ser encontradas na maioria dos livros de cálculo de uma variável real e, em particular, em Cálculo 1, volume 1, aulas 9 e 10:
Algumas demonstrações serão apresentadas aqui.
Derivadas de Funções Básicas
A derivada de $x^a$, $a \in \mathbb R$.
Seja $a$ um número real e considere a função $f(x)=x^a$ para todo $x \in \mathbb R\setminus \{0\}$. Então $f$ é diferenciável no seu domínio e $f'(x) = a x^{a-1}$.
Optamos por não apresentar a demonstração geral aqui. Todavia, pode ser interessante conhecer uma demonstração do caso particular $a \in \mathbb N$. A intenção não é tanto provar o resultado, mas apresentar uma forma de argumentar conhecida como "indução matemática", bastante usada. Ressaltamos que não haverá prejuízo para o aluno se a leitura dessa prova for postergada para uma segunda oportunidade.
Seja $n$ um número natural e considere a função $f(x)=x^n$ para todo $x \in \mathbb R$. Então, $f$ é diferenciável no seu domínio e $f'(x) = n x^{n-1}$.
Demonstração:
A ideia aqui é desenvolver a demonstração com os seguintes passos:
Mostramos que o resultado vale para $n=0$.
Mostramos que se o resultado vale para algum valor $n=N$, ele valerá para $n = N+1$. (Isso é: se for verdade para $n=5$, por exemplo, também será para $n=6$.)
Como já teremos provado que o resultado vale para $n=0$, podemos concluir que valerá para $n = 0+1= 1$. Mas aí já saberemos que vale para $n=1$ e, portanto, valerá para $n= 1+1 =2$. Se valer para $n=2$, valerá para $n=3$ e, por esse argumento (conhecido como argumento de indução) mostraremos que o resultado é verdade para todo expoente natural.
Passamos, então, à demonstração.
a) O resultado vale para $n=0$.
Suponha que $n=0$ e, portanto, estamos falando da função constante $f(x) = x^0 =1$ e devemos mostrar que $f'(x) = 0x^{0-1}=0$. Para calcular a derivada, escrevemos:
$$f'(x_0) = \lim_{x \to x_0} \frac{f(x) - f(x_0)}{x-x_0} = \lim_{x \to x_0}\frac{1-1}{x-x_0} = 0.$$b) Se o resultado vale para $n=N$, também valerá para $n=N+1$.
Suponha que vale para $n=N$. Isto é, $(x^N)'= Nx^{N-1}$. Precisamos mostrar que $(x^{N+1})' = (N+1) x^N$. Se $f(x) = x^{N+1}$, escrevemos a derivada como:
$$\begin{array}{lll}f'(x_0)& = &\lim_{x \to x_0} \frac{f(x) - f(x_0)}{x-x_0} \\& & \\& = & \lim_{x \to x_0} \frac{x^{N+1} - {x_0}^{N+1}}{x-x_0} \\& & \\& = & \lim_{x \to x_0} \frac{x^N(x-x_0)-x_0({x_0}^N-x^N)}{x-x_0}\\& & \\& = & \lim_{x \to x_0}\left(x^N + x_0 \frac{x^N -{x_0}^N}{x-x_0}\right)\\& & \\& = & x_0^N + x_0\lim_{x \to x_0}\frac{x^N -{x_0}^N}{x-x_0} \mbox{ (usando que o resultado vale para n=N)} \\& & \\& = & x_0^N + Nx_0\cdot x_0^{N-1}\\& & \\& = & x_0^N(1+N),\end{array}$$portanto, vale para $n=N+1$.
Assim, por indução, mostramos a proposição.
No Teorema 1, excluímos $x=0$. O que acontece nesse caso? Bem, depende do expoente. Se o expoente for negativo, por exemplo, a função não será nem definida em $x=0$. Se o expoente for positivo, mas menor do que $1$, e tentarmos derivar usando o Teorema, obteremos, na derivada, um expoente negativo e a derivada não será definida em $x=0$. Esse caso está tratado nos exemplos. Se o expoente for maior ou igual a $1$, o Teorema vale em $x=0$.
A derivada do seno
Seja $\displaystyle f(x)= \mathrm{sen} (x)$ para todo $x \in \mathbb{R}$, estudemos a derivabilidade de $f$. Vamos usar aqui a definição de derivada na forma:
$$f'(x) = \lim_{h \to 0}\frac{f(x+h) -f(x)}{h}.$$Seja $x \in \mathbb{R}$ arbitrário. Para todo $h \neq 0$, temos
\begin{array}{lll}\displaystyle\frac{f(x+h)-f(x)}{h} & = &\displaystyle\frac{\mathrm{sen} (x+h) - \mathrm{sen}(x)}{h}\\ \\ & = &\displaystyle\frac{\mathrm{sen} x \cos h + \cos x\ \mathrm{sen} h - \mathrm{sen} x}{h}\\ \\ & = &\cos x \left( \displaystyle\frac{\mathrm{sen} h}{h} \right) + \mathrm{sen} x \left(\displaystyle\frac{\cos h -1}{h}\right). \end{array}
Sabemos que $\displaystyle\lim_{h \to 0} \frac{\mathrm{sen} h}{h} = 1$ e $\displaystyle\lim_{h \to 0} \frac{\cos h - 1}{h} = 0$.
Concluímos que:
\begin{array}{lll}f'(x) & = &\displaystyle\lim_{h \to 0} \displaystyle\frac{f(x+h)-f(x)}{h}\\ \\ & = &\cos x \displaystyle\lim_{h \to 0} \left( \displaystyle\frac{\mathrm{sen} h}{h} \right) + \mathrm{sen}(x) \displaystyle\lim_{h \to 0} \left(\displaystyle\frac{\cos h -1}{h}\right)\\ \\ & = &\cos x. \end{array}
Acabamos de mostrar que $f$ é derivável em $\mathbb{R}$ e $f'(x)= \cos x$.
Apresentamos alguns resultados formais. A partir de agora, esses resultados (e outros, que serão enunciados com menos formalismo) constituirão a base para uma série de exemplos. Todas as demonstrações e formalizações podem ser consultadas na bibliografia da disciplina.
Cálculos de Derivadas (soma, produto e quociente).
Vamos apresentar nessa seção, de forma esquemática, as derivadas de algumas funções e algumas regras (fórmulas) para derivar soma, produto e quociente de funções. Essas informações serão a base para a construção de vários exemplos. O objetivo agora não é ser formal nem desenvolver teorias, mas apresentar ferramentas de cálculo. Não faremos, portanto, as demonstrações. Elas podem ser encontradas na maioria dos livros de cálculo de uma variável real e, em particular, em Cálculo 1, volume 1, aulas 9 e 10:
Com o objetivo de sermos sucintos, apresentamos as derivadas das funções elementares em forma de tabela. A discussão do domínio de cada uma das funções derivadas será feita nos exemplos.
| $f(x)$ | $x^{a}$ | $e^{x}$ | $\ln(x)$ | $\mathrm{sen}(x)$ | $\cos(x)$ |
| $f'(x)$ | $ax^{a-1}$ | $e^{x}$ | $\frac{1}{x}$ | $\cos(x)$ | $-\mathrm{sen}(x)$ |
Derivada das funções elementares.
Regras de Derivação
Suponha que $f: \mathrm{D} \subset \mathbb{R} \longrightarrow \mathbb{R}$ e $g: \mathrm{D} \subset \mathbb{R} \longrightarrow \mathbb{R}$ são funções diferenciáveis em $\mathrm{D}$. Então, para todo $x$ em $\mathrm{D}$, valem os resultados seguintes:
\begin{equation}\tag{1} (f + g)'(x) = f'(x) + g'(x). \end{equation} \begin{equation} \tag{2}(fg)'(x) = f'(x)g(x) + g'(x)f(x). \end{equation} \begin{equation} \tag{3} \mbox{Se } g(x) \neq 0 \mbox{ então } \left(\frac{f(x)}{g(x)}\right)'= \frac{f'(x) g(x) - g'(x) f(x)}{g^2(x)}. \end{equation} \begin{equation} \tag{4} \mbox{Se } k \mbox{ é constante em } \mathbb R, \; (kf)'(x) = k f'(x). \end{equation}Usando a tabela 2 e as regras em 1, 2, 3 e 4 vamos fazer alguns exemplos.
Se $f(x) = x^4$, usamos a tabela que diz que $(x^a)'= a x^{a-1}$ e, portanto:
$(x^4)'= 4x^3$.
Se $f(x) = 5x^3$ usamos a regra 4 para escrever $(5x^3)' = 5(x^3)'$ e, usando a expressão da derivada de $x^a$, escrevemos:
$5(x^3)' = 5 \cdot 3 x^2 = 15 x^2$.
Generalizando os dois exemplos anteriores, vemos que para derivar qualquer expressão do tipo $k x^a $ podemos fazer:
$$(kx^a)' = k (x^a)' = kax^{a-1}.$$como sabemos de 1 que a derivada da soma é a soma das derivadas, vemos que é possível derivar qualquer polinômio. Por exemplo:
\[\begin{array}{lll}(3x^5-6x^3 + 2x)' & = & 3\cdot 5 x^{5-1} - 6 \cdot 3 x^{3-1} + 2\cdot 1 x^{1-1} \\& = & 15 x^4 - 18 x^2 +2.\end{array}\]Aqui, é importante observar que as regras confirmam aquilo que nossa intuição geométrica já havia percebido. Por exemplo, se o gráfico de $f(x)$ é uma reta com equação $ y = ax +b$, podemos usar as regras de derivação para escrever $y' = (a x^{1} + b x^0)' = ax^{1-1} + b\cdot0 x^{0-1} = a$. Assim, concluímos que o coeficiente angular da reta tangente a uma reta, é o próprio coeficiente angular da reta, como era de se esperar. Em especial, se a reta é horizontal, o coeficiente angular da reta tangente vale $0$ pois se $y = b$, escrevemos $y = bx^0 $ e derivamos: $y' = b\cdot0\cdot x^{-1} = 0$.
Quanto vale $(\sqrt{x})'$?
Escrevemos $\sqrt{x} = x^{1/2}$ e mais uma vez usamos a tabela para derivar: $(x^{1/2})' = \frac{1}{2} x^{1/2-1} = \frac{1}{2\sqrt{x}}$. Note que ${f'}_+(0)$ não pode ser definida por essa expressão. Na verdade, uma análise do gráfico da função raiz, permite verificar que a reta tangente em $x=0$ coincide com o eixo $y$ e, portanto, teria coeficiente angular infinito (se fizesse sentido dizer isso).
Mesmo que, nesse momento, nossa preocupação maior seja fazer as contas quase mecanicamente, não podemos nos descuidar de interpretar os resultados. O próximo exemplo traz uma função contínua em $\mathbb R$ cuja derivada não está definida em todos os pontos.
Considere $f(x) = x^{1/3}$. Usando as fórmulas, derivamos $f$ como $f'(x) = \frac{1}{3} x^{\frac{1}{3}-1} = \frac{1}{3}x^{-2/3} = \frac{1}{x^{2/3}}$. Evidentemente, a derivada que calculamos não está definida em $x=0$, embora a função esteja.
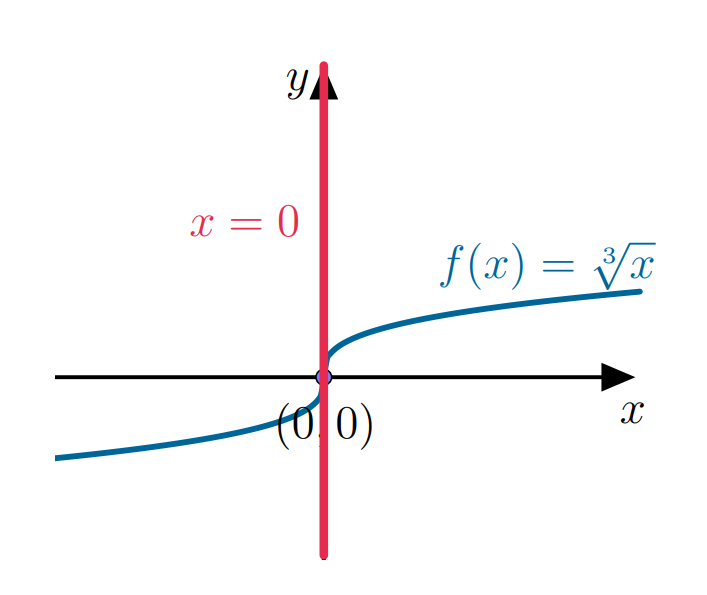
Gráfico de $f(x) = x^{1/3}$.
Considere a função $ f(x) = |x|$, $x \in \mathbb R$ definida como:
\[|x|=\left\{\begin{array}{ccc}-x & \mbox{se} & x<0, \\x & \mbox{se} & x \geq 0.\end{array} \right.\]O gráfico de $f$ está na figura abaixo:
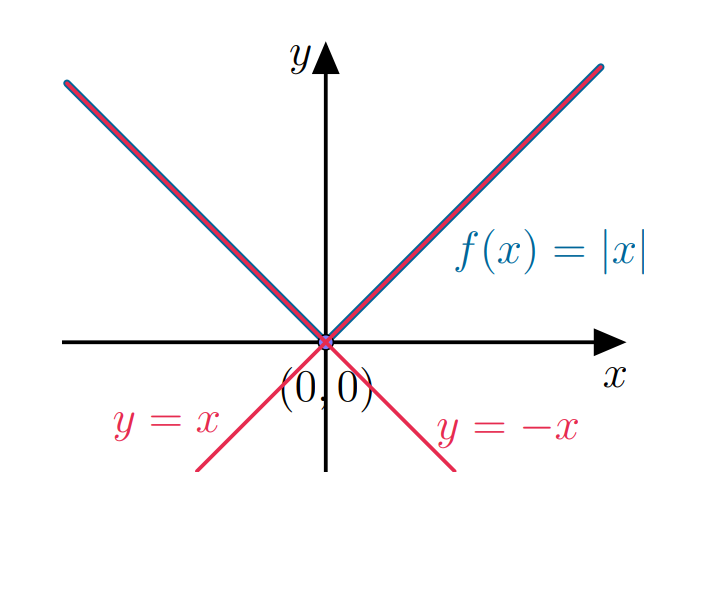
Se derivarmos a expressão de $f(x)$, $x \neq 0$, teremos qual função?
A função $h: \mathbb{R} \to \mathbb{R}$ definido por $h(x)=\mathrm{sen}(x) \cos(x)$ para todo $x \in \mathbb{R}$, é derivável em $\mathbb{R}$ e $h'(x)=\cos^2 (x) - \mathrm{sen}^2 (x)$, para todo $x \in \mathbb{R}$. Definamos as funções $f(x)=\mathrm{sen}(x)$ e $g(x)=\cos(x)$ para todo $x \in \mathbb{R}$, então $h=fg$. Vamos usar a regra do produto.
\begin{array}{lll}h'(x)& = &f'(x)g(x)+g'(x)f(x) \\& & \\& = & (\cos(x)) \cos(x) + (-\mathrm{sen}(x)) \mathrm{sen} (x) \\& & \\& = & \cos^2 x - \mathrm{sen}^2 x.\\& & \\\end{array}
Qual a derivada de $(x^2 \cos(x))' $?
Aqui temos um produto. Usando a regra 2 escrevemos:
\[(x^2 \cos(x))' = (x^2)' \cos(x) + x^2 \cos'(x) = 2x \cos(x) - x^2 \mathrm{sen}(x).\]Escreva a equação da reta tangente ao gráfico de $f(x) = e^x (2x^4 + 3x) $ no ponto $(1,5e)$.
Vamos resolver passo-a-passo.
A função é diferenciável porque é produto de funções diferenciáveis.
O ponto $(1,5e)$ no gráfico corresponde a $x=1$ no domínio. Portanto, $f'(1)$ é o coeficiente angular da reta tangente procurada.
$f'(x) = (e^x)' (2x^4 + 3x) + e^x (2x^4 + 3x)'$ pela regra do produto 2.
Calculando a derivada, temos $f'(x) = e^x (2x^4+3x) + e^x (8x^3 +3) $.
Avaliando em $x=1$, $f'(1) = 16e$.
Precisamos da reta com coeficiente angular $16e$ , contendo o ponto $(1,5e)$. Portanto, $y = 5e + 16e(x-1)$. (Observação: Não há, a menos que seja explicitamente pedido, necessidade de fazer mais nenhuma conta. Todavia, alguns alunos se \sentem desconfortáveis em não ver uma equação na forma $y = ax+b$. Nada impede que a equação seja reescrita como: $ y = 16e x + (5e -16)$).
Calcule a derivada de $f(x) = \mathrm{cotg}(x), \; x \neq n\pi, \; n \in \mathbb Z$.
Aqui, temos um quociente, pois $\mathrm{cotg} (x) = \frac{\cos(x)}{\mathrm{sen}(x)}$. Os valores de $x$ que anulam o denominador não estão no domínio de $f$ mas, é preciso lembrar que a função tem assíntotas verticais. Vamos fazer a conta e, depois, tomar cuidado com isso.
\[\begin{array}{lll}(\mathrm{cotg})'(x)& = & \left(\dfrac{\cos(x)}{\mathrm{sen}(x)}\right)' = \dfrac{\cos' (x) \mathrm{sen}(x) - \mathrm{sen}' (x)\cos(x)}{\mathrm{sen}^2 (x)}\\& & \\& = & \dfrac{-\mathrm{sen}^2 (x) - \cos^2 (x) }{\mathrm{sen}^2 (x)} \\& & \\& = & \dfrac{-1}{\mathrm{sen}^2 (x)} = -\csc^2 (x).\end{array}\]Então, temos $(\mathrm{cotg})'(x) = -\csc^2 (x)$, $x \neq n \pi$, $ n \in \mathbb Z$.
Se $ f(x) = \frac{3x^2 + 5x}{\ln(x)}, \; x>0 \text{ e } x \neq 1$ então usamos a regra do quociente 3 para escrever:
Seja $f(x)=\frac{x^7-9x^4}{x^2-1}$ para todo $x \in \mathbb{R}-\{-1,1\}$, calculemos $f'(x)$. Temos um quociente de polinômios e, portanto, sabemos da regra do quociente 3 que para todo $x \in \mathbb{R}-\{-1,1\}$, as funções $x^7-9x^4$ e $x^2-1$ são deriváveis.
\begin{array}{111} f'(x) & = &\dfrac{(x^7-9x^4)'(x^2-1)-(x^7-9x^4)(x^2-1)'}{(x^2-1)^2}\\ \\ & = &\dfrac{(7x^6-36x^3)(x^2-1)-(x^7-9x^4)(2x)}{(x^2-1)^2}.\end{array}Seja $f(x)= \tan x$, definida para $x \in \mathbb{R}$, $x \neq (2k+1) \frac{\pi}{2}$, onde $k \in \mathbb{Z}$. Calculemos $f'(x)$.
Como $f(x)=\frac{\mathrm{sen} (x)}{\cos(x)}$, e sabendo que as funções $\mathrm{sen} (x)$ e $\cos(x)$ são deriváveis, pela regra do quociente 3 sabemos que $f$ é derivável e
\begin{array}{111} f'(x) & = &\dfrac{(\mathrm{sen} (x))'(\cos (x))-(\mathrm{sen}(x))(\cos(x))'}{\cos^2 x}\\ \\ & = &\dfrac{(\cos(x))(\cos(x))-(\mathrm{sen}(x))(-\mathrm{sen} x)}{\cos^2 x}\\ \\ & = &\dfrac{\cos^2 x + \mathrm{sen} ^2 x}{\cos^2 x} = \dfrac{1}{\cos^2 x} = \sec^2 x,\end{array}para todo $x \in \mathbb{R}$, $x \neq (2k+1) \frac{\pi}{2}$.

