Lista 3

Exercício 1

Em cada um dos gráficos a seguir, discuta a existência dos limites laterais e do limite propriamente dito nos pontos a indicados.


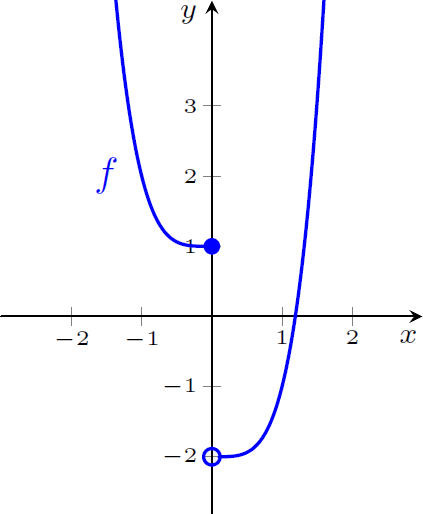
Figura 1: $a=0$


Figura 2: $a=-1$


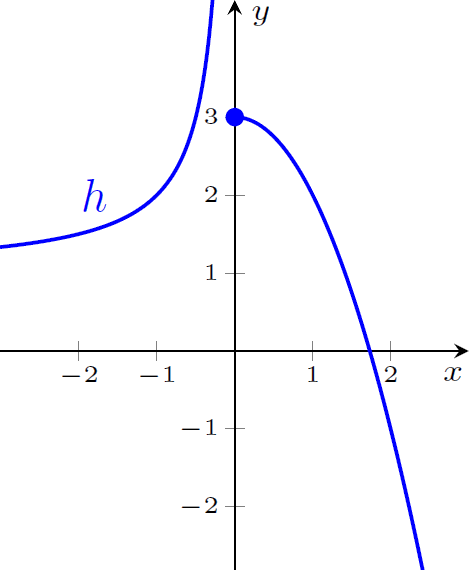
Figura 3: $a=0$

Solução

Na Figura 1 temos que o limite à esquerda vale $1$, o limite à direita vale $-2$. Não existe o limite em $a=0$ pois os limites laterais são diferentes. Na Figura 2 temos que o limite à esquerda vale $2$, o limite à direita vale $2$. Portanto, $\displaystyle \lim_{x \rightarrow a} f(x)=2$. Na Figura 3 temos que o limite à esquerda não existe pois a função não se aproxima de nenhum valor finito, o limite à direita vale $3$. Não existe o limite em $x=a$.

Exercício 2

Considerando o gráfico de h representado à direita, determine caso exista o $\displaystyle \lim_{x \rightarrow 0} h(x^2+3)$.


Solução

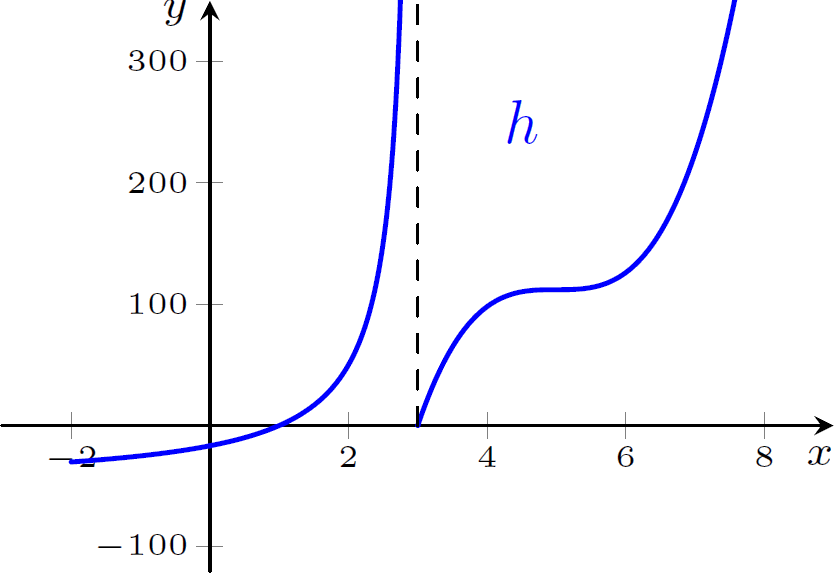
Temos que $\displaystyle \lim_{x \rightarrow 0^-} h(x^2+3)=\displaystyle \lim_{y\rightarrow 3^+} h(y)=0$ e $\displaystyle \lim_{x\rightarrow0^+} h(x^2+3)=\displaystyle \lim_{y\rightarrow3^+}h(y)=0$. Como os limites laterais são iguais, então $\displaystyle \lim_{x\rightarrow0^+} h(x^2+3)=0$.

Exercício 3

Em cada um dos exercícios abaixo calcule o limite (se existir) das funções no ponto a indicado. Se o limite não existir, explique por quê.

  1. $a=1, f(x)=\displaystyle \frac{3x-5}{2x+1}, \space x \in \mathbb{R} \backslash \{-1/2\}$

  2. $a=\pi, f(x)= \mathrm{ln}(x) \cdot \mathrm{sen}(x), \space x \in (0,\infty)$

  3. $a=\pi/4, f(x)=\mathrm{cos}(x)-\mathrm{sen}(x), \space x \in \mathbb{R}$

  4. $a=1^+, f(x)=\displaystyle \frac{ln(x)}{e^x}, \space x>1$

  5. $a=2, f(x)=\begin{cases} 2x+1, & \text{se } x>2\\3x-1, & \text{se } x<2 \end{cases} $

  6. $a=2, f(x)=\begin{cases} 2x+3, & \text{se } x>2\\3x-1, & \text{se } x<2 \end{cases} $

Solução

  1. $-2/3$;

  2. $0$;

  3. $0$;

  4. $0$;

  5. $\displaystyle \lim_{x\rightarrow2^+} f(x) =5$, e $\displaystyle \lim_{x\rightarrow2^-} f(x)=5 \Rightarrow \displaystyle \lim_{x\rightarrow2} f(x)=5$

  6. $\displaystyle \lim_{x\rightarrow2^+} f(x) =7$, e $\displaystyle \lim_{x\rightarrow2^-} f(x)=5 \Rightarrow \nexists \displaystyle \lim_{x\rightarrow2^+} f(x)$

Exercício 4

Considere:

$f(x)=\begin{cases} e^x+2, & \text{se } x>2\\3x+1, & \text{se } x<1 \end{cases} $ e $f(x)=\begin{cases} x^2+1, & \text{se } x<0\\x^3, & \text{se } x<1 \end{cases} $

Estude $\displaystyle \lim_{x \rightarrow 0} f \circ g(x)$

Solução

Se $x\rightarrow0^-$, $g(x)\rightarrow1^+$, porque para valores de $x$ menores que $0$, $g(x)=x^2+1$ e $x^2+1>1$. Se $x\rightarrow1^+$, $f(x)\rightarrow e + 2$. Portanto, $\displaystyle \lim_{x\rightarrow0^-} f\circ g(x)=e+2$. Se $x\rightarrow0^+$, $g(x)\rightarrow0^+$ e $\displaystyle \lim_{x\rightarrow0^+} f(x)=1$. Portanto, $\displaystyle \lim_{x\rightarrow0^+} f\circ g(x)=1$. Conclusão: Não existe o limite da composta, porque os limites laterais são diferentes.

Exercício 5

Em cada um dos itens abaixo calcule os limites laterais (se existirem) e discuta a existência do limite no ponto $a$ indicado:

  1. $a=2, f(x)=\displaystyle \frac{(x^2-4)^2}{(x-2)^2(x+3)}$

  2. $a=0, f(x)=\displaystyle \frac{e^x-1}{e^x+1}$

  3. $a=1, f(x)=\displaystyle \frac{ln(x^2)}{2x-4}$

  4. $a=1, f(x)=\displaystyle \frac{x^3+x+2}{x-1}$

  5. $a=1, f(x)=\displaystyle \frac{|x-1|}{x^2-1}$

Solução

  1. $16/5$

  2. $0$

  3. $0$

  4. O limite não existe.

  5. O limite não existe pois os limites laterais são distintos, $\displaystyle \lim_{x\rightarrow1^+} \frac{|x-1|}{x^2+1}=\frac{1}{2}$ e $\displaystyle \lim_{x\rightarrow1^-} \frac{|x-1|}{x^2-1}=-\frac{1}{2}$

Exercício 6

Seja $f(x)=2x, x\in\mathbb{R}$. Encontre uma expressão para $\displaystyle \lim_{x \rightarrow 3} f^n(x)$ onde $f^n$ é a composta da função $f$ um número $n$ de vezes: $f^n=f\circ f\circ \overset{n}{\cdots} \circ f$, ou seja, $n$ vezes ($n\geq1$).

Solução

Observe

$$f(x)=2x,$$ $$f^2(x)=f\circ f(x)=f(f(x))=f(2x)=2(2x)=2^2x,$$ $$f^3(x)=f\circ f\circ f\circ f(x)=f(f\circ f(x))=f(f^2(f(x))-f(2^2x)=2(2^2x)=2^3x,$$ $$\cdots$$

Assim $f^n(x)=2^n(x)$ para qualquer $n\geqslant1$. Finalmente, obtemos que $\displaystyle \lim{x\rightarrow3} f^n(x)=2^n\cdot3$.

Exercício 7

Em cada um dos itens abaixo, determine:

  1. $\displaystyle \lim_{x\rightarrow-1} \frac{2x^2-3x-5}{x+1}$

  2. $\displaystyle \lim_{x\rightarrow2} \frac{\sqrt{4x+1}-3}{x-2}$

  3. $\displaystyle \lim_{x\rightarrow-3} \frac{x^3+5x^2+7x+3}{2x^3+9x^2+10x+3}$

  4. $\displaystyle \lim_{x\rightarrow0} \frac{\sqrt{1+x}-\sqrt{1-x}}{x}$

  5. $\displaystyle \lim_{x\rightarrow-1} \frac{\sqrt[3]{x}+1}{x+1}$

  6. $\displaystyle \lim_{x\rightarrow-1} \frac{\sqrt[3]{x}-\sqrt[3]{a}}{x-a}$

Solução

  1. $\displaystyle \lim_{x\rightarrow-1}\frac{2x^2-3x-5}{x+1}=\displaystyle \lim_{x\rightarrow-1} \frac{(x+1)(2x-5)}{x+1}=\displaystyle \lim_{x\rightarrow-1}(2x-5)=-7$

  2. $\displaystyle \lim_{x\rightarrow2}\frac{\sqrt{4x+1}-3}{x-2}=\displaystyle \lim_{x\rightarrow2}\frac{(\sqrt{4x+1}-3)}{(x-2)}\cdot\frac{(\sqrt{4x+1}-3)}{(\sqrt{4x+1}-3)}=\displaystyle \lim_{x\rightarrow2}\frac{4(x-2)}{(x-2)(\sqrt{4x+1}-3)}=\displaystyle \lim_{x\rightarrow2}\frac{4}{(\sqrt{4x+1}-3)}=\frac{2}{3}$

  3. $\displaystyle \lim_{x\rightarrow-3} \frac{x^3+5x^2+7x+3}{2x^3+9x^2+10x+3}=\displaystyle \lim_{x\rightarrow-3}\frac{(x+1)^2(x+3)}{(x+1)(x+3)(2x+1)}=\displaystyle \lim_{x\rightarrow-3}\frac{(x+1)^2}{(x+1)(2x+1)}=\frac{2}{5}$

  4. $\displaystyle \lim_{x\rightarrow0}\frac{\sqrt{1+x}-\sqrt{1-x}}{x}=\displaystyle \lim_{x\rightarrow0}\frac{\sqrt{1+x}-\sqrt{1-x}}{x}\cdot\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}=\displaystyle \lim_{x\rightarrow0}\frac{1+x-(1-x)}{x(\sqrt{1+x}+\sqrt{1-x})}=\displaystyle \lim_{x\rightarrow0}\frac{2x}{x(\sqrt{1+x}+\sqrt{1-x})}=\displaystyle \lim_{x\rightarrow0}\frac{2}{(\sqrt{1+x}+\sqrt{1-x})}=\frac{2}{2}=1$

  5. $\displaystyle \lim_{x\rightarrow-1} \frac{\sqrt[3]{x}+1}{x+1}=\displaystyle \lim_{x\rightarrow-1} \frac{\sqrt[3]{x}+1}{x+1}\cdot\frac{\sqrt[3]{x^2}-\sqrt[3]{x}+1}{\sqrt[3]{x^2}-\sqrt[3]{x}+1}=\displaystyle \lim_{x\rightarrow-1} \frac{x+1}{(x+1)(\sqrt[3]{x^2}-\sqrt[3]{x}+1)}=\displaystyle \lim_{x\rightarrow-1} \frac{1}{(\sqrt[3]{x^2}-\sqrt[3]{x}+1)}=\frac{1}{3}$

  6. $\displaystyle \lim_{x\rightarrow a} \frac{\sqrt[3]{x}-\sqrt[3]{a}}{x-a}=\displaystyle \lim_{x\rightarrow a} \frac{\sqrt[3]{x}-\sqrt[3]{a}}{x-a}\cdot\frac{\sqrt[3]{x^2}+\sqrt[3]{ax}+\sqrt[3]{a^2}}{\sqrt[3]{x^2}+\sqrt[3]{ax}+\sqrt[3]{a^2}}=\displaystyle \lim_{x\rightarrow a}\frac{x-a}{(x-a)(\sqrt[3]{x^2}+\sqrt[3]{ax}+\sqrt[3]{a^2})}=\displaystyle \lim_{x\rightarrow a} \frac{1}{\sqrt[3]{x^2}+\sqrt[3]{ax}+\sqrt[3]{a^2}}=\frac{1}{3\sqrt[3]{a^2}}=\frac{\sqrt[3]{a}}{3a}$

Exercício 8

Seja $f:\mathbb{R} \rightarrow \mathbb{R}$ uma função tal que $\displaystyle \lim_{x\rightarrow0} \frac{f(x)}{x}=1$. Determine:

  1. $\displaystyle \lim_{x\rightarrow0} \frac{f(3x)}{x}$

  2. $\displaystyle \lim_{x\rightarrow0} \frac{f(x-1)}{x-1}$

Solução

  1. $\displaystyle \lim_{x\to 0} \dfrac{f(3x)}{x} = \displaystyle \lim_{x\to 0} \dfrac{f(3x)\cdot3}{x\cdot3} \\ = 3 \cdot \displaystyle \lim_{x\to 0} \dfrac{f(3x)}{3x} = 3 \cdot \displaystyle \lim_{t\to 0} \dfrac{f(t)}{t} = 3$.

  2. $\displaystyle \lim_{x\to 1} \dfrac{f(x-1)}{x-1} = \displaystyle \lim_{t\to 0} \dfrac{f(t)}{t} = 1$.

Exercício 9

  1. $\displaystyle \lim_{x\rightarrow0} x^2 \space \mathrm{sen} \left(\frac{1}{x}\right)$

  2. $\displaystyle \lim_{x\rightarrow0} x^{27} \space \mathrm{cos} \left(\frac{1}{49x}\right)$

  3. $\displaystyle \lim_{x\rightarrow0^+} \sqrt{x}\space e^{\mathrm{sen} \left(\dfrac{\pi}{x}\right)}$

  4. $\displaystyle \lim_{x\rightarrow0} (\mathrm{cos}(x)-1)\space \mathrm{sen} \left(\frac{1}{x}\right)$

  5. $\displaystyle \lim_{x\rightarrow-1} (2x^2+x-1)\mathrm{cos}\left(\frac{1}{x+1}\right)$

Solução

Em todos os itens aplicaremos o teorema do anulamento. Para isso, lembramos que precisamos comprovar que a função, cujo limite queremos calcular, se pode escrever como produto de uma função limitada por uma função com limite zero.

  1. $\displaystyle \lim_{x\to0} x^2\cdot \mathrm{sen}(\frac{1}{x})=0$

  2. $\displaystyle \lim_{x\to0} x^{27}\cdot \mathrm{cos}\left(\frac{1}{49x}\right)=0$

  3. $\displaystyle \lim_{x\to0^+} \sqrt{x}\cdot e^{\mathrm{sen}\left(\dfrac{\pi}{x}\right)}=0$

  4. $\displaystyle \lim_{x\to0} (\mathrm{cos}(x)-1)\mathrm{sen}\left(\frac{1}{x}\right)=0$

  5. $\displaystyle \lim_{x\to-1} (2x^2+x-1)\cdot\mathrm{cos}\left(\frac{1}{x+1}\right)=0$

Exercício 10

Determine:

  1. $\displaystyle \lim_{x\rightarrow0} \frac{\mathrm{sen}(2020x)}{x}$

  2. $\displaystyle \lim_{x\rightarrow0} \frac{\mathrm{tg}(x)}{x}$

  3. $\displaystyle \lim_{x\rightarrow p} \frac{\mathrm{tg}(x-p)}{x^2-p^2}; p\neq0$

  4. $\displaystyle \lim_{x\rightarrow0} \frac{\mathrm{sen}(x-3)}{|x^2-2x-3|}$

  5. $\displaystyle \lim_{x\rightarrow0} \frac{1-\mathrm{sen}(x)}{2x-\pi}$

Solução

  1. $\displaystyle \lim_{x\to0}\frac{\mathrm{sen}(2020x)}{x}=\displaystyle \lim_{x\to0}\frac{\mathrm{sen}(2020x)\cdot2020}{x\cdot2020}=2020\cdot\displaystyle \lim_{y\to0}\frac{\mathrm{sen}(y)}{y}=2020$

  2. $\displaystyle \lim_{x\to0}\frac{\mathrm{tg}(x)}{x}=\displaystyle \lim_{x\to0}\frac{\mathrm{sen}(x)}{x \space \mathrm{cos}(x)}=\displaystyle \lim_{x\to0}\frac{\mathrm{sen}(x)}{x}\cdot\displaystyle \lim_{x\to0}\frac{1}{\mathrm{cos}(x)}=1$

  3. $\displaystyle \lim_{x\to p}\frac{\mathrm{tg}(x-p)}{x^2-p^2}=\displaystyle \lim_{x\to p}\frac{\mathrm{tg}(x-p)}{(x-p)(x-p)}=\displaystyle \lim_{h\to0}\frac{\mathrm{tg}(h)}{h(h+2p)}=\frac{1}{2p}$

  4. Como temos um módulo no denominador e $x^2-2x-3=(x-3)(x-1)$ tem sinais diferentes à esquerda e à direita de $3$, vamos calcular os limites laterais.

     

    $\displaystyle \lim_{x\to3^-}\frac{\mathrm{sen}(x-3)}{|x^2-2x-3|}=\displaystyle \lim_{x\to3^-}\frac{\mathrm{sen}(x-3)}{-(x-3)(x+1)}=\displaystyle \lim_{x\to3^-}\frac{-1}{x+1}\cdot\displaystyle \lim_{x\to3^-}\frac{\mathrm{sen}(x-3)}{x-3}=\left(-\frac{1}{4}\right)\cdot\displaystyle \lim_{t\to0^-}\frac{\mathrm{sen}(t)}{t}=-\frac{1}{4}$

     

    Analogamente, $\displaystyle \lim_{x\to3^+}\frac{\mathrm{sen}(x-3)}{|x^2-2x-3|}=\frac{1}{4}$, portanto $\displaystyle \lim_{x\to3}\frac{\mathrm{sen}(x-3)}{|x^2-2x-3|}$ não existe.

     

  5. $\displaystyle \lim_{x\to\frac{\pi}{2}}\frac{1-\mathrm{sen} \space x}{2x-\pi}=\displaystyle \lim_{t\to0}\frac{1-\mathrm{sen}\left(t+\dfrac{\pi}{2}\right)}{2t}=\displaystyle \lim_{t\to0}\frac{1-\mathrm{sen}(t)\space\mathrm{cos}\left(\dfrac{\pi}{2}\right)-\mathrm{cos}(t)\space\mathrm{sen}\left(\dfrac{\pi}{2}\right)}{2t}=\displaystyle \lim_{t\to0}\frac{1-\mathrm{cos}(t)}{2t}$

    $\text{portanto, }\displaystyle \lim_{t\to0}\frac{1-\mathrm{cos}(t)}{2t}=\displaystyle \lim_{t\to0}\frac{1-\mathrm{cos}(t)}{2t}\cdot\frac{1+\mathrm{cos}(t)}{1+\mathrm{cos}(t)}=\displaystyle \lim_{t\to0}\frac{1-\mathrm{cos}^2(t)}{2t\cdot(1+cos(t))}=\displaystyle \lim_{t\to0}\frac{\mathrm{sen}^2(t)}{2t\cdot(1+\mathrm{cos}(t))}=\frac{1}{2}\cdot\displaystyle \lim_{t\to0}\frac{\mathrm{sen}(t)}{t}\cdot\displaystyle \lim_{t\to0}\frac{\mathrm{sen}(t)}{1+\mathrm{cos}(t)}=0$

Exercício 11

Assumindo que $\displaystyle \lim_{x\rightarrow0} x \cdot \mathrm{cosec}(x)=1$, calcule $\displaystyle \lim_{x\rightarrow0} \frac{\mathrm{tg}(3x)}{\mathrm{sen}(4x)}$

Solução

$\displaystyle \lim_{x\to0}\frac{\mathrm{tg}(3x)}{\mathrm{sen}(4x)}=\displaystyle \lim_{x\to0}\frac{\mathrm{tg}(3x)}{\mathrm{sen}(4x)}\cdot\frac{12x}{12x}=\displaystyle \lim_{x\to0}\frac{3}{4}\cdot\frac{\mathrm{tg}(3x)}{3x}\cdot\frac{4x}{\mathrm{sen}(4x)}=\frac{3}{4}\displaystyle \lim_{y\to0}\frac{\mathrm{tg}(y)}{y}\cdot\displaystyle \lim_{t\to0}\frac{t}{\mathrm{sen}(t)}=\frac{3}{4}$