Funções inversas
A Noção Intuitiva
A noção de função inversa é bastante natural. Grosso modo, podemos imaginar que uma função realiza determinada operação sobre um valor do seu domínio e a inversa deve "desfazer" essa operação e retornar ao ponto inicial. Se o domínio de uma função é um conjunto de pessoas e a operação é subir escada é bastante intuitivo que a operação inversa deveria ser: descer escada. Da mesma forma, se o domínio é um conjunto de folhas de papel e a operação sobre cada elemento do conjunto é dobrar papel, também parece razoável sugerir que operação inversa seja desdobrar papel. Esses dois exemplos, ingênuos e imprecisos, podem dar informações importantes sobre as principais características daquilo que o senso comum chama de "inverso"; a matemática trará precisão e formalismo a essa noção.
Duas coisas devem ser ressaltadas nos dois exemplos:
-
Se as duas operações são efetuadas consecutivamente, o elemento que sofre as alterações retorna a seu estado inicial. Ou seja, se alguém sobe uma escada, depois desce, não sai do lugar; ou se começa em cima, desce e depois sobe, também não sai do lugar. Da mesma forma, se uma folha de papel é dobrada e, depois, desdobrada, ela não se altera; ou, se um papel dobrado é desdobrado e dobrado novamente, ele volta ao seu estado "inicial". O que se pode extrair desse senso comum para o universo matemático? Espera-se que, se duas funções são uma inversa da outra, quando avaliadas consecutivamente, não alteram o elemento em que foram avaliadas. Qual a operação que pode traduzir a ideia de avaliação consecutiva? A composição! Pensando desse modo seria coerente dizer que dadas duas funções reais, representadas por $f$ e $g$, $g$ será inversa de $f$ se $g\circ f (x) = x$, para qualquer $x$, ou $f \circ g (y) = y$ para qualquer $y$.
Só pode subir quem está em baixo e só pode descer, quem está em cima. Da mesma forma, só pensamos em dobrar o papel desdobrado e só desdobramos o que já foi dobrado. A ideia, traduzida para o formalismo matemático, é que uma função $f$ e sua inversa não são avaliadas no mesmo conjunto. Só faz sentido pensar na inversa de $f$ como "inversa" de alguma coisa, em valores que já foram previamente calculados por $f$. Em outras palavras, a inversa de $f$ tem domínio na Imagem de $f$. Se chamarmos de $x$ o elemento em que $f$ é calculada e de $y$ o elemento na Imagem de $f$ ($f(x)=y$), a inversa de $f$ será calculada em $y$.
Formalizando a Intuição
Vamos proceder dando uma roupagem mais científica e formal às noções que comentamos anteriormente. Estamos falando de funções e isso exige que sejam explicitados domínio e imagem. Vamos chamar de $\mathrm{D}(f)$ o domínio de $f$ e de $x$ um elemento de $\mathrm{D}(f)$. Por conveniência, vamos escolher o conjunto Imagem de $f$ para contradomínio (discutiremos a adequação dessa escolha posteriormente) e representar por $y$ um elemento na Imagem de $f$. Traduzimos isso considerando uma função:
\[\begin{array}{lccl}f: & \mathrm{D} \subseteq \mathbb{R} & \longrightarrow & Im(f) \subseteq \mathbb{R} \\& x & \longmapsto & y\end{array}\]Definimos agora uma função, que chamaremos de $f^{-1}$ cujo domínio é a imagem de $f$ e o contradomínio é $\mathrm{D}$ e representamos como:
\[\begin{array}{lccl}f^{-1}: & Im(f) \subseteq \mathbb{R} & \longrightarrow & \mathrm{D} \subseteq \mathbb{R} \\& y & \longmapsto & x\end{array}\]E, finalmente, formalizamos a definição:
Dadas duas funções:
\[\begin{array}{lcl}\begin{array}{lccl}f: & \mathrm{D} \subseteq \mathbb{R} & \longrightarrow & Im(f) \subseteq \mathbb{R} \\& x & \longmapsto & y\end{array} \mbox{ e } &\begin{array}{lccl}f^{-1}: & Im(f) \subseteq \mathbb{R} & \longrightarrow & \mathrm{D} \subseteq \mathbb{R} \\& y & \longmapsto & x\end{array}\end{array}\]dizemos que $f^{-1}$ é a função inversa de $f$ se e somente se, para todo $x$ em $\mathrm{D}(f)$, $f^{-1} \circ f (x) =x$ ou, equivalentemente, para todo $y$ na imagem de $f$, $f \circ f^{-1} (y) = y$.
Esquematicamente, estamos pensando como:
\[\begin{array} {lll}x &\stackrel{f} \longmapsto & y \\& \stackrel{f^{-1}} \longleftarrow&\end{array}\]Considere $f(x) = 2x -3, \; x\in \mathbb{R}$. Podemos ver que $f$ "atua" sobre a variável $x$ multiplicando por 2 e subtraindo $3$. Se, ao calcular $f$, obtemos um valor $y$, é razoável pensar que somando $3$ a $y$ e dividindo por $2$, teremos a função inversa. Esquematicamente:
$$$$ \[\begin{array}{ccccc}& \textcolor{blue}{\times 2} & & \textcolor{blue}{-3} & \\x &\longmapsto & 2x &\longmapsto & 2x-3 = y \\\frac{y+3}{2} & \longleftarrow & y+3 &\longleftarrow y \\ & \textcolor{blue}{\div 2} & &\textcolor{blue}{+3}\end{array}\]São dadas as funções $f$ e $g$ a seguir:
\[\begin{array}{lcl}\begin{array}{lccc}f : &(-1, \infty) &\longrightarrow & Im(f) \\& x & \longmapsto & \sqrt{e^{3x+2}} = y\end{array}& \mbox{ e }\begin{array}{lccc}g : & Im(f) &\longrightarrow & (-1,\infty) \\& y & \longmapsto & \left( \frac{\ln y^2-2}{3}\right)\end{array}\end{array}\]aonde $Im(f)$ é o conjunto imagem de $f$. Vamos verificar se $g$ é inversa de $f$. Para isso, basta verificar se $f\circ g(y) = y $ ou $g \circ f(x) =x$; se uma das condições acontecer, a outra necessariamente acontece
Aqui, escolhemos domínio e contradomínio de modo a garantir bijetividade. A necessidade dessa escolha será discutida posteriormente.
Vamos calcular $g \circ f(x)$:
\[\begin{array}{lcl}g \circ f (x) & = & g (\sqrt{e^{3x+2}}) \\& = & \frac{\ln(y^2)-2}{3} \\& = & \frac{\ln \left(\sqrt{e^{3x+2}}\right)^2-2}{3} \\& = & \frac{\ln(e^{3x+2}) -2}{3} \\& = & \frac{{3x+2-2}}{3} \\& = & \frac{1}{3} (3x) = x\end{array}\]A Existência da Função Inversa
Pensar se uma função $f: A \rightarrow B$ tem uma função inversa é um processo relativamente independente de determinar essa função (caso exista). Em geral, é bastante improvável, para uma função arbitrária, que se consiga determinar uma fórmula para sua inversa, mesmo quando se tem certeza que a função é inversível. Queremos determinar condições para que a inversa exista, mesmo quando não possa ser explicitada.
Dada uma função $f: A \longrightarrow B$, sabemos que a função inversa deve ser definida com domínio em $B$ e contradomínio em $A$. Isso significa que todo elemento de $b \in B$ precisa ter uma correspondência com um elemento $a \in A$ de tal modo que $f(a) = b$. Para que isso aconteça é necessário que $B$ seja a imagem de $f$. Em outras palavras, $f$ deve ser sobrejetora. O Diagrama de Venn na figura ??? ilustra o que acontece quando a Imagem de $f$ e o contradomínio ($B$) são diferentes, isto é: existem elementos em $B$ que não são imagem de nenhum valor em $A$. Se tomarmos, por exemplo, $F \in B$ na figura, não será possível determinar $f^{-1} (F)$ e, portanto, não teremos uma função inversa com domínio em $B$.
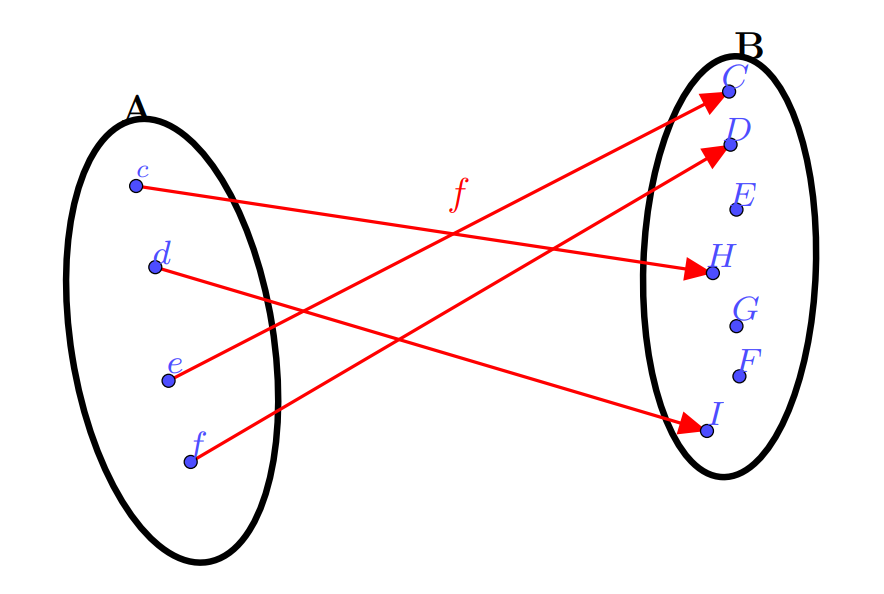
O contradomínio é diferente da imagem
Uma segunda condição é que todo elemento $b \in B$ deve ter uma correspondência com um único elemento de $A$ para que, mais uma vez, a definição de função seja satisfeita. Para que isso ocorra, dados $a_1$ e $a_2$ em $A$ precisamos garantir que $f(a_1) \neq f(a_2)$. Em outras palavras, $f$ deve ser injetora. O diagrama de Venn a seguir ilustra o que pode acontecer se a função não for injetora. Se tomarmos $\mathrm{D}$ na imagem de $f$, vemos que a relação inversa pode associá-lo a dois valores distintos e, portanto, não será uma função.
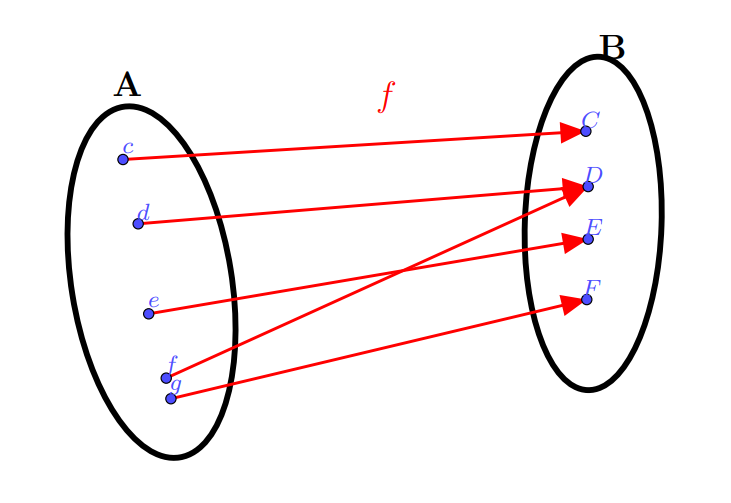
A função não é injetora.
As duas condições mencionadas implicam que $f$ deve ser bijetora. De um modo geral, a sobrejetividade sempre pode ser garantida escolhendo a Imagem de $f$ como contradomínio; a injetividade precisa ser verificada.
Vamos verificar se a função $f: \mathbb{R}^+ \longrightarrow \mathbb{R}$ descrita por $f(x)=\sqrt{x^3 +2}$ tem uma função inversa.
$f$ é injetora?
$f$ é sobrejetora?
Escolha $x_1$ e $x_2$ em $\mathbb{R}^+$. Suponha que $\sqrt{{x_1}^3 +2} = \sqrt{{x_2}^3 +2}$. Então, elevando ao quadrado dos dois lados, temos ${x_1}^3 +2 = {x_2}^3 +2$ e, portanto ${x_1}^3 = {x_2}^3 $ o que nos permite concluir que $x_1 = x_2$ e $f$ é injetora. (importante atentar para o fato de que trabalhamos em $\mathbb{R}^+$ o tempo todo).
Não é difícil ver que a Imagem de $f$ é sempre positiva e, portanto, $f$ não é sobrejetora.
Assim, a função $f$ não é inversível. Todavia, podemos definir uma nova função $g: \mathbb{R}^+ \longrightarrow (\sqrt{2}, \infty)$ que será inversível, com $g(x)= \sqrt{x^3+2}$ pois escolhemos o contradomínio igual à Imagem de $f$.
Considere a relação que a cada $x$ associa o valor $-x^2 +3x+1$.Vamos definir uma função inversível (isto é: escolher domínio e contradomínio) com essa relação. Se tomarmos $\mathbb{R}$ como domínio sabemos que o gráfico será uma parábola com concavidade para baixo como na figura ???. Podemos escolher vários intervalos aonde a função é injetora. Qualquer intervalo que não contenha o ponto $(3/2, 0)$ (o vértice da parábola) no seu interior, serviria. Escolhemos para domínio o intervalo $\left(\frac{-3-\sqrt{13}}{2}, \infty\right)$ e contradomínio $\mathbb{R}^-$. Escolhemos o intervalo cujo limite inferior é a raiz positiva e o gráfio nos conta que a imagem é $\mathbb{R}^-$. Por isso, tomamos essa imagem como contradomínio.
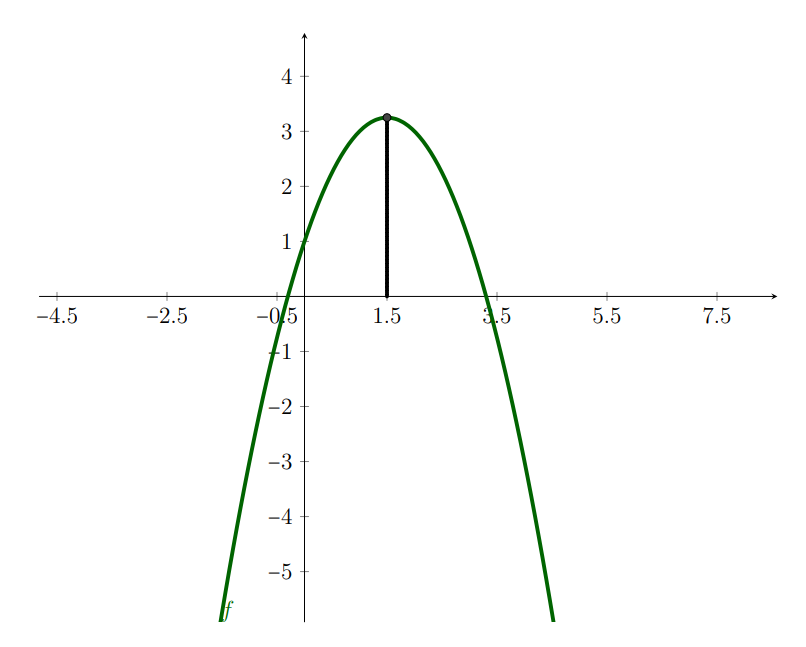
É possível escolher vários intervalos aonde a função terá inversa.
Cabe observar que o estudo de existência da inversa (mesmo quando não pode ser calculada) é de suma importância. Imagine, por exemplo, que determinada função $f(x)$ associa o grau de poluição do subsolo com a quantidade de defensivos agrícolas encontrada em um produto. Se soubermos que essa função é inversível, por exemplo, podemos mensurar a variação de contaminação do subsolo, medindo a contaminação do produto.
Sob o ponto de vista matemático, é interessante notar que funções inversíveis têm propriedades que podem ser deduzidas da inversibilidade. Por exemplo, uma função inversível em determinado domínio, sempre será monótona - crescente ou decrescente - naquele domínio; também, se a função for monótona, será inversível. A figura ??? ilustra o que acontece quando a função não é monótona. Como, nesse caso, ela cresce e depois decresce (ou vice-versa) alguma reta horizontal, ($y = constante$) vai interceptar o gráfico de $f$ em mais de um ponto.Todos os pontos de intersecção (da forma $(x,k)$) têm a mesma imagem, mas os valores da primeira coordenada ($x$) em cada um deles é diferente. Esse comportamento mostra que a função não é injetora.
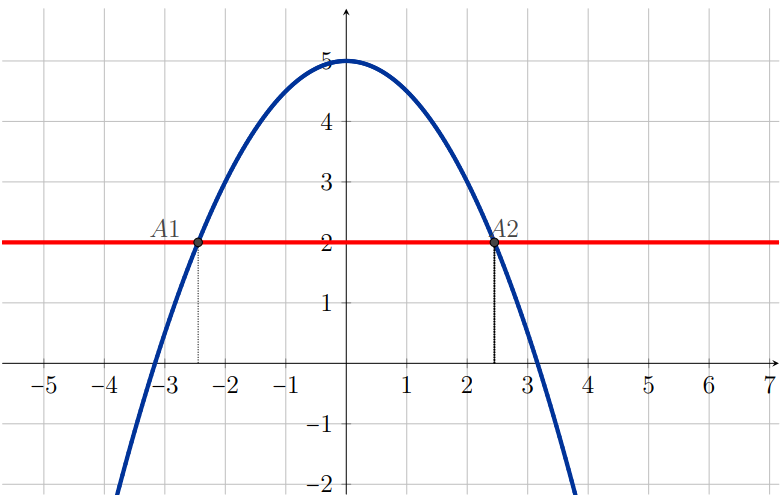
Se a função não for monótona, existe uma reta horizontal que intersecta o gráfico em mais de um ponto, o que mostra que a função não é injetora.
Relação Entre o Gráfico da Função e o Gráfico da Inversa
Para as funções:
\[\begin{array}{lcl}\begin{array}{cccc}f: & A &\longrightarrow & B \\& a & \longmapsto & b\end{array}& \mbox{ e } &\begin{array}{cccc}f^{-1}: & B &\longrightarrow & A \\& b & \longmapsto & a\end{array}\end{array}\]sabemos que $(a,b)$ pertence ao gráfico de $f$ se e somente se $(b,a)$ pertende ao gráfico de $f^{-1}$. A figura ??? ilustra o fato de que os pontos $(a,b)$ e $(b,a)$ são simétricos em relação à reta $y = x$. Por essa razão, é frequente, para traçar o gráfico da inversa, fazer o rebatimento (em relação à essa reta) do gráfico da função. Esse procedimento é útil mas deve ser feito com o entendimento de que, ao fazer isso, estamos "misturando os eixos". Se olharmos só o gráfico da função, o eixo horizontal representa o domínio de $f$. Se olharmos só o gráfico da inversa, o eixo horizontal representará a imagem da função $f$, pois será o domínio da inversa.

Note a simetria entre os pontos $(a,b)$ e $(b,a)$.
A figura ??? mostra o gráfico de $f(x) = \frac{x^3}{8}$ e de sua inversa. Observe a simetria em relação à reta $y = x$.

Note a simetria em relação à reta $y = x$ da função e de sua inversa.
A Noção de Inverso Na Matemática
Essa parte é opcional. Ela se propõe a localizar a noção de função inversa dentro de um contexto um pouco mais geral na matemática. Para isso, discutimos como a noção de inverso se apresenta em algumas situações conhecidas e fazemos a analogia com a ideia de função inversa. A leitura dessa parte pode ser omitida sem que haja prejuízo ao aluno no sentido do conteúdo esperado em Cálculo-1A.
Se você perguntar a alguém qual o inverso, por exemplo, do número $3$ é provável que a resposta seja $1/3$ ou, ainda, $-3$. Se essa pessoa souber um pouquinho a respeito de matrizes e você perguntar pelo inverso de uma matriz $A$, é provável que ela mencione aquela matriz $A^{-1}$ cuja característica é descrita pela equação: $AA^{-1} = A^{-1}A = Id$ em que $Id$ é a matriz conhecida como matriz identidade. Nossa intenção, aqui, é entender o que esses casos têm em comum e qual a relação com a ideia de função inversa.
O que nos leva a achar que $1/3$ é uma boa opção para ser ``o inverso" de $3$ é o fato de que $(1/3)\cdot 3 = 1$. O que o número $1$ tem de tão especial? Bem, o $1$ é o único número que, quando se considera a operação de multiplicação, não altera o elemento que está sendo multiplicado. Sabemos que $1x = x1 = x$, para todo $x$. Em outras palavras, o $1$ não tem efeito sobre a multiplicação de reais e é conhecido como elemento neutro da multiplicação. Assim, quando mencionamos, por exemplo $1/4$ como inverso de $4$, estamos aludindo ao fato de que a multiplicação de $4$ por $1/4$ conduz ao elemento neutro da multiplicação.
Pensando dessa forma, se considerarmos a operação de soma, o número $0$ é o elemento neutro da soma de reais, já que $0+x = x+0 =x$. Em outras palavras, um número não se altera quando somado ao $0$. Dentro dessa perspectiva, poderíamos dizer que,quando consideramos o conjunto dos reais com a operação de soma, o inverso de $3$ é $-3$ já que $3 + (-3) = \mbox{ elemento neutro da soma}$.
Se olharmos para o conjunto de matrizes quadradas, $n \times n$, inversíveis, com a operação de multiplicação de matrizes, a matriz conhecida como $Id_{n \times n}$, que contem o número $1$ na diagonal e o número $0$ nas outras posições faz o papel de elemento neutro da operação. Pois, $A\dot Id_{n \times n} = \dot Id_{n \times n} A = A$. Isto é, uma matriz $A$ não se modifica quando multiplicada pela matriz identidade. E a matriz conhecida como inversa de $A$ é justamente aquela que, multiplicada por $A$, tem como resultado a Identidade.
Podemos pensar um pouco, à luz desses exemplos, como a noção de função inversa se insere nessas ideias. Vamos analisar o conjunto de todas as funções reais com imagem real com a operação de composição. A função que vai atuar como elemento neutro desse conjunto é aquela que - não por acaso - é chamada função identidade e definida por $id(x) = x, \; x \in \mathbb{R}$. Observe que, dada qualquer função $f$ no conjunto, $id \circ f (x) = f \circ id(x) = f$. Ou seja, a função $id(x)$, quando composta com outra do conjunto, não altera essa outra. É, portanto, o elemento neutro da operação de composição. É neste pano de fundo que definimos a função inversa de $f$: ela é a função $g$ que ``operada'' (com a operação de composição) com $f$ nos dá o elemento neutro da composição.
Discutimos alguns exemplos do uso da noção de inverso em matemática. Resumindo, é frequente que essa palavra apareça associada a um conjunto com uma operação que tem um elemento neutro, que será a identidade da operação. E a noção do inverso de um elemento aparece associada à ideia de que, um elemento do conjunto ``operado" com o seu inverso (se existir) terá como resultado a identidade dessa operação nesse conjunto.

