As funções seno hiperbólico e cosseno hiperbólico são definidas, respectivamente, por
\[ \mathrm{cosh}(x)=\frac{e^x+e^{-x}}{2} \qquad \text{e} \qquad \mathrm{senh}(x)=\frac{e^x-e^{-x}}{2}.\]Mostre que $\mathrm{cosh}^2(x) - \mathrm{senh}^2(x) = 1$.
Isto mostra que o ponto de coordenadas $\left(\mathrm{cosh}(x), \mathrm{senh}(x)\right)$ está sobre a hipérbole de equação $x^2-y^2=1$. Para refletir sobre o que isto representa e comparar com o seno e o cosseno tradicionais (também chamados de circulares), lembre-se de que o ponto $\left(\cos(x), \mathrm{sen}(x)\right)$ está sobre o círculo de equação $x^2+y^2=1$.
Mostre que $\mathrm{cosh}'(x) = \mathrm{senh}(x)$ e $\mathrm{senh}'(x) = \mathrm{cosh}(x)$.
Definindo $\mathrm{tgh}(x)=\dfrac{\mathrm{senh}(x)}{\mathrm{cosh}(x)}$ e $\mathrm{sech}(x)=\dfrac{1}{\mathrm{cosh}(x)}$, calcule $\mathrm{tgh}'(x)$ e $\mathrm{sech}'(x)$. Você percebe alguma semelhança com as derivadas de $\mathrm{tg}$ e $\sec$ ?
\begin{eqnarray}\mathrm{cosh}^2(x) - \mathrm{senh}^2(x) &=&\left( \dfrac{e^x+e^{-x}}{2}\right)^2 - \left( \dfrac{e^x-e^{-x}}{2}\right)^2 \\ \\& = & \dfrac{e^{2x}+2e^x e^{-x}+e^{-2x}}{4} - \dfrac{e^{2x}-2e^x e^{-x}+e^{-2x}}{4}=\dfrac{4e^{x}e^{-x}}{4}=\dfrac{4}{4}=1\end{eqnarray}
$$\mathrm{cosh}'(x) = \left( \dfrac{e^x+e^{-x}}{2}\right)'= \dfrac{e^x-e^{-x}}{2}=\mathrm{senh}(x)$$
$$ \text{e}$$
$$\mathrm{senh}'(x) = \left( \dfrac{e^x-e^{-x}}{2}\right)'= \dfrac{e^x-(-e^{-x})}{2}=\mathrm{cosh}(x)$$-
Aplicando a Regra do Quociente:
\begin{eqnarray}\mathrm{tgh}'(x) & = &\left( \dfrac{\mathrm{senh}(x)}{\mathrm{cosh}(x)}\right)=\dfrac{\mathrm{senh}'(x)\mathrm{cosh}(x)-\mathrm{senh}(x)\mathrm{cosh}'(x)}{\mathrm{cosh}^2(x)} \\ \\ & = & \dfrac{\mathrm{cosh}^2(x)-\mathrm{senh}^2(x)}{\mathrm{cosh}^2(x)} =\dfrac{1}{\mathrm{cosh}^2(x)}=\mathrm{sech}^2(x).\end{eqnarray} \begin{eqnarray}\qquad \qquad \mathrm{sech}'(x) & = &\left(\dfrac{1}{\mathrm{cosh}(x)}\right)' \\ \\& = & \dfrac{-\mathrm{cosh}'(x)}{\mathrm{cosh}^2(x)}=-\dfrac{1}{\mathrm{cosh}(x)}\dfrac{\mathrm{senh}(x)}{\mathrm{cosh}(x)} \\ \\& = &-\mathrm{sech}(x)\mathrm{tgh}(x).\end{eqnarray}
Muitos fenômenos naturais, como crescimento populacional ou decaimento radioativo ou de concentração, são caracterizados por terem a derivada da função envolvida proporcional ao valor da própria função, ou seja,
\[f'(x) = \alpha \cdot f(x).\]Para $C$ e $\alpha$ reais, calcule a derivada da função definida por $f(x) = C\,e^{\alpha\,x}$ e verifique que $f$ satisfaz a condição $f'(x) = \alpha \cdot f(x)$.
Dê 2 funções diferentes que satisfazem a condição $f'(x) = -2\,f(x)$.
Uma determinada população de animais pode ser aproximada por uma função $P(t)$, em função do tempo $t$ em anos, satisfazendo $P'(t) = 0,1\cdot P(t)$. Se a população inicial (isto é, quando $t=0$) é de 1.000.000 indivíduos, determine uma possível expressão para a função $P(t)$.
A concentração de um determinado remédio, quando no sangue humano, é dada pela função $c(t)$, com $t$ medido em horas. A derivada desta concentração é proporcional ao valor da própria concentração, isto é, $c'(t)=\alpha\cdot c(t)$. Determine uma possível expressão para esta concentração, sabendo que a concentração inicial é $0,5$ml por litro de sangue e que a concentração uma hora depois é $3,03265$ml por litro de sangue.
Observação: Em Cálculo 2A, você verá que as possíveis expressões encontradas nos itens 3 e 4 são, na realidade, a única possibildiade para as funções.
$f'(x)=\alpha C e^{\alpha x}=\alpha \cdot f(x)$.
$f_1(x)= 3e^{-2x}$ e $f_2(x)= -e^{-2x}$
Pelo item~1, podemos pensar que a função é da forma $P(t)=C e^{0,1t}$. Como $C=P(0)=1000000$, então $P(t)=1000000 e^{0,1t}$.
Pelo item~1, podemos pensar que a função é da forma $c(t)=0,5 \cdot e^{\alpha t}$. Como $c(1)=3,03265 \iff 0,5\cdot e^{\alpha}=3,03265 \iff e^{\alpha}=6,0653 \iff \alpha=\ln(6,0653) \approx 1,8951$
Derive as funções dos itens abaixo (se for conveniente, use derivação logarítmica)
$f(x)=e^{\sqrt x}\ln{\sqrt x}$
$f(x)=\ln\left(x\sqrt{x^2+1}\right)$
$f(x)=\left(e^x\right)^{x}$
$f(x)=\ln\dfrac{\sqrt{x+1}}{(x-1)^3}$
-
Aplicando a regra do produto e regra da cadeia: $f'(x)=\left(e^{\sqrt x}\ln{\sqrt x}\right)'= \dfrac{1}{2\sqrt{x}}e^{\sqrt{x}} \ln \sqrt{x} + e^{\sqrt{x}} \dfrac{\frac{1}{2\sqrt{x}}}{\sqrt{x}}= \dfrac{\sqrt{x}\ln \sqrt{x}}{2x} e^{\sqrt{x}} + e^{\sqrt{x}} \dfrac{1}{2x} =\dfrac{e^{\sqrt x}\left(1+\sqrt x \ln {\sqrt x}\right)}{2x}$
-
Aplicando a regra do produto e regra da cadeia: $f'(x)=\left(\ln\left(x\sqrt{x^2+1}\right)\right)' = \dfrac{\sqrt{x^2+1}+x\frac{x}{\sqrt{x^2+1}}}{x\sqrt{x^2+1}} = \dfrac{\frac{x^2+1+x^2}{\sqrt{x^2+1}}}{x\sqrt{x^2+1}} = \dfrac{2x^2+1}{x\left(x^2+1\right)}$
Note que $f(x)=\left(e^x\right)^x=e^{x^2}$. Apesar que para calcular $f'(x)$ pode diretamente derivar usando a regra de derivação da função exponencial e da cadeia, também podemos aplicar $\ln$ em ambos os lados obtendo $\ln f(x)=x^2$ e derivando
$$\frac{f'(x)}{f(x)}=2x \iff f'(x) = 2xf(x)=2x\left(e^x\right)^x$$Como $f(x)=\ln\dfrac{\sqrt{x+1}}{(x-1)^3}=\ln \sqrt{x+1}-3\ln(x-1)$, então
$f'(x)=\dfrac{1}{2\sqrt{x+1}}\dfrac{1}{\sqrt{x+1}}-\dfrac{3}{x-1} = \dfrac{1}{2(x+1)}-\dfrac{3}{x-1}=\dfrac{x-1-6(x+1)}{2(x^2-1)} = -\dfrac{5x+7}{2(x^2-1)}$
Dadas constantes reais $\mu$ e $\sigma$, podemos definir a Distribuição Normal de Gauss através da função
\[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\]Esta é a função mais utilizada na Probabilidade, para modelar fenômenos naturais ou mesmo ligados ao comportamento humano. O número $\mu$ é chamado de esperança e indica o ``centro'' do gráfico. Já o número real $\sigma$ é chamado de desvio padrão, e está relacionado ao formato da curva; quanto maior o valor de $\sigma$, mais baixa e aberta é a curva, quanto menor, mais alta e pontuda ela é. Alguns exemplos abaixo:
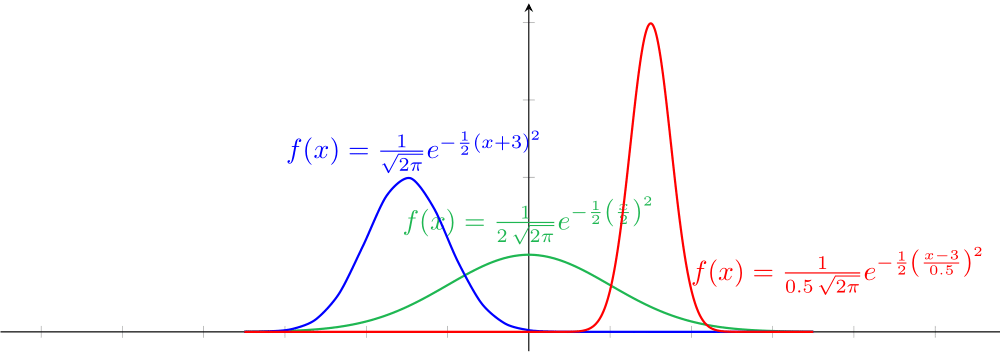
Verde:$\mu=0$ e $\sigma=2$ Azul:$\mu=-3$ e $\sigma=1$ Vermelho:$\mu=3$ e $\sigma=0.5$
Calcule $f'(x)$.
Determine os intervalos em que $f$ é crescente e descrescente.
Verifique que $f(\mu+k) = f(\mu-k)$ para todo $k \in \mathbb{R}$. Com isso, o gráfico de $f$ é simétrico em relação à reta $x=\mu$.
Calcule $\displaystyle\lim_{x\to-\infty} f(x)$ e $\displaystyle\lim_{x\to+\infty} f(x)$.
$f'(x)=\dfrac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\left(-\dfrac{1}{\sigma^2}\right)\left(\dfrac{x-\mu}{\sigma}\right)=-\frac{1}{\sigma^4\sqrt{2\pi}}\left(x-\mu\right)e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$.
A função $f$ é crescente quando $f'(x)>0$, ou seja para $x<\mu$ e é decrescente quando $f'(x)<0$, ou seja para $x>\mu$.
Basta calcular $f(\mu+k)$ e $f(\mu-k)$.
$\displaystyle\lim_{x\to \pm \infty} f(x)=\displaystyle\lim_{x\to \pm \infty} \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}=0$, porque o expoente da exponencial tende a $-\infty$.
Calcule $y'$ nos itens abaixo
$\mathrm{sen}({e^{xy}})=x$
$\dfrac{y^2 \cos (x)}{e^x}=2^{\ln(y)}$, para $x=0$ e $y=1$
Usando regra da cadeia para derivar implicitamente $\mathrm{sen}({e^{xy}})=x$, obtemos
$(y+xy')e^{xy}\cos(e^{xy})=1 \Rightarrow y'xe^{xy}\cos(e^{xy})= 1 - ye^{xy}\cos(e^{xy}) \Rightarrow y'=\dfrac{1-ye^{xy} \cos(e^{xy})}{x e^{xy} \cos(e^{xy})}$.
Temos que $\dfrac{y^2 \cos (x)}{e^x}=e^{-x}y^2 \cos (x)$ e $2^{\ln y}=e^{\ln y \ln 2}$. Derivando implicitamente a equação $e^{-x}y^2 \cos (x)=e^{\ln y \ln 2}$ obtemos:
$$-e^{-x}y^2 \cos (x)+e^{-x}2yy' \cos(x) -e^{-x}y^2 \mathrm{sen} (x)= \dfrac{\ln 2 y'}{y}e^{\ln 2 \ln y}$$Para $x=0$ e $y=1$ temos $-1+2y'= \ln 2 y'$. Logo $y'=\dfrac{1}{2-\ln 2}$.
Nos itens a seguir verifique se o Teorema de Rolle pode ser aplicado a $f$ nos intervalos indicados.
$f(x)=(x-3)(x+1)^2, \ \ x\in [-1,3]$
$f(x)=x-x^{\frac{1}{3}},\ \ x\in [0,1]$
$f(x)=x-x^{\frac{1}{3}},\ \ x\in [-1,1]$
Sim
Sim
Não, $f$ diferenciável em $(-1,1)$ não se verifica, pois $f$ não é diferenciável em $x=0\in (-1,1)$.
A altura de uma bola, $t$ segundos após o lançamento, é dada por $f(t)=-16t^2+48 t+32$.
Verifique que $f(1)=f(2)$;
Segundo o Teorema de Rolle, qual deve ser a velocidade $v$ da bola em algum instante do intervalo $[1,2]$? Enuncie o Teorema de Rolle;
Encontre a velocidade média da bola durante os dois primeiros segundos;
Em que instante a velocidade instantânea é igual à velocidade média acima? Enuncie o teorema que nos garante isso.
$f(1)=f(2)=64$
$v=0$
$16$ m/seg
$t=1$ seg
Seja $f:[-1,2]\longrightarrow \mathbb{R}$ contínua em $[-1,2]$, diferenciável em $(-1,2)$, com $f(-1)=-1$ e $f(2)=5$. Prove que existe um ponto no gráfico de $f$ em que a reta tangente é paralela à reta $y=2x$.
Existe uma reta tangente ao gráfico e paralela à reta $y=2x$ $\Longleftrightarrow \exists x \in [1,2]\ \text{ tal que } f'(x)=2$ (coeficientes angulares iguais). Calcule o coeficiente angular da reta secante ao gráfico que contém os pontos $(-1,f(-1))$ e $(2,f(2))$, depois aplique o Teorema do Valor Médio (TVM).
Seja $p(x)=Ax^2+Bx+C$. Prove que, para qualquer intervalo $[a,b]$, o valor de $c$ cuja existência é garantida pelo Teorema do Valor Médio (TVM), é o ponto médio do intervalo.
(i) $p$ é contínua em $[a,b]$ pois $p$ é uma função polinomial; (ii) $p$ é diferenciável em $(a,b)$ pois $p$ é uma função polinomial. Se valem as hipóteses (i) e (ii) do TVM, então vale a tese: $\exists c\in (a,b)$ tal que
\begin{eqnarray} p'(c) &=&\dfrac{p(b)-p(a)}{b-a}=\dfrac{\left(Ab^2+Bb+C\right)-\left(Aa^2+Ba+C\right)}{b-a} =\dfrac{A\left(b^2-a^2\right)+B(b-a)}{b-a} \\ \\&=&\dfrac{A(b-a)(b+a)+B(b-a)}{b-a}=\dfrac{(b-a)[A(b+a)+B]}{b-a}= A(b+a)+B.\end{eqnarray}Além disso, como $p'(x)=2Ax+B$, temos que $p'(c)=2Ac+B$.
Igualando as duas expressões de $p'(c)$ e simplificando, chegamos a $c=\dfrac{a+b}{2}$.
Se $a>0$ e $n$ é um inteiro não negativo qualquer, prove que $p(x)=x^{2n+1}+ax+b$ não pode ter duas~raízes~reais.
Suponha, por absurdo, que $p(x)$ tem duas raízes reais $x_1$ e $x_2$ com $x_1 < x_2$. Observe que as hipóteses do Teorema de Rolle para $p$ em $[x_1,x_2]$ são verdadeiras: (i) $p$ é contínua em $[x_1,x_2]$, (ii) $p$ é diferenciável em $(x_1,x_2)$ pois $p$ é uma função polinomial e (iii) $p\left(x_1\right)=p\left(x_2\right)=0$ pois $x_1$ e $x_2$ são raízes de $p(x)$. Portanto, podemos aplicar o Teorema de Rolle:
\begin{equation} \tag{1}\exists c\in (x_1,x_2) \quad \text{tal que} \ \ p'(c)=0.\end{equation}Por outro lado, $p'(x)=(2n+1)x^{2n}+a=(2n+1)\left(x^n\right)^2+a$. Como, $(2n+1)\left(x^n\right)^2\geq 0$, para todo $x\in \mathbb{R}$ e por hipótese $a>0$, temos que
\begin{equation} \tag{2} p'(x)>0, \quad \forall x\in\mathbb{R} \end{equation}Finalmente observe que as conclusões 1 e 2 são contraditórias. Logo não é possível supor que existem duas raízes reais.
Mostre que $g(x)=8x^3+30x^2+24x+10$ admite uma única raiz no intervalo $(-3,-2)$.
$1{^{a}}$parte: Como a função polinomial $g$ é contínua em $[-3,-2]$, $g(-3)=-8<0$ e $g(-2)=18>0$, pelo Teorema do Valor Intermediário, $g$ possui pelo menos uma raiz entre $-3$ e $-2$.
$2{^{a}}$parte: Suponha, por absurdo, que $g$ admite duas raízes $c_1$ e $c_2$ tal que $-3<c_1 < c_2<-2$. Logo $g(c_1)=g(c_2)=0$. Como a função polinomial $g$ é contínua em $[-3,-2]$ e diferenciável em $(-3,-2)$, pelo Teorema de Rolle,
\begin{equation} \tag{3}\exists c \in (-3,-2)\ \ \text{entre $c_1$ e $c_2$ tal que $g'(c)=0$}.\end{equation}Por outro lado, $g'(x)=24x^2+60x+24=12(x+2)(2x+1)$. Analisando o sinal de $g'(x)$, temos $g'(x)>0$ quando $-3<x<-2$. Em particular $g'(c)>0$, que contradiz com~3. Conclusão: $g$ não admite duas raízes entre $-3$ e $-2$.
Pela $1{^{a}}$ parte, $g$ possui pelo menosuma raiz entre $-3$ e $-2$ e pela $2{^{a}}$ parte, $g$ não admite duas raízes entre $-3$ e $-2$, consequentemente $g$ possui uma única raiz entre $-3$ e $-2$.
Seja $P$ uma função polinomial não constante.
Prove que, entre dois zeros consecutivos de $P'$ (isto é, dois valores de $x$ que anulam a derivada e tal que entre eles não existe outro valor que anula a derivada), existe no máximo uma raiz de $P$.
Se $P$ tem três raízes distintas em $[a,b]$, prove que $P''(c)=0$, para algum valor $c \in (a,b)$.
Suponha que $x_1$ e $x_2$ são dois zeros consecutivos de $P'$. Suponha, por absurdo, que entre $x_1$ e $x_2$ existem duas raízes de $P$. Sejam $x_3$ e $x_4$, com $x_3<x_4$ essas raízes de $P$. Assim, $\left(x_3,x_4\right)\subset\left(x_1,x_2\right)$.
Aplicando o Teorema de Rolle para a função $P$ em $\left[x_3,x_4\right]$: $\left[\mathrm{(i)} P\left(x_3\right)=P\left(x_4\right)=0\right]$, verifique as outras duas hipóteses, afirmamos que $\exists \ c\in \left(x_3,x_4\right)\subset\left(x_1,x_2\right)$ tal que $P'(c)=0 \Longrightarrow$ $\exists \ c\in \left(x_1,x_2\right)$ tal que $P'(c)=0$, o que contradiz com a hipótese de que $x_1$ e $x_2$ são dois zeros consecutivos de $P'$.
Sejam $x_1$, $x_2$ e $x_3$ as três raízes, com $x_1<x_2<x_3$. O Teorema de Rolle aplicado a $P$ nos intervalos $\left[x_1,x_2\right]$ e $\left[x_2,x_3\right]$ nos garante (verifique as hipóteses) que $\exists \ c_1 \in\left(x_1,x_2\right)$ e $\exists \ c_2 \in\left(x_2,x_3\right)$ tais que $P'\left(c_1\right)=P'\left(c_2\right)=0$. Agora, o Teorema de Rolle aplicado a $P'$ no intervalo $\left[c_1,c_2\right]$ nos garante (verifique as hipóteses) que $\exists \ c \in\left(c_1,c_2\right)$ tal que $P''\left(c\right)=0$.
Calcule os limites dos itens abaixo.
$\displaystyle\lim_{x\rightarrow{0}}\dfrac{\cos^2(x)-1}{e^{x^2}-1}$
$\displaystyle\lim_{x\rightarrow{(3\pi/2)^{+}}}(\sec(x)-\mathrm{tg}(x))$
$\displaystyle\lim_{x\rightarrow{+\infty}}{\left(x^2-1\right)e^{-x^2}}$
$\displaystyle\lim_{x\rightarrow{+\infty}}\dfrac{\ln{(\ln(x)})}{\ln (x)}$
$\displaystyle\lim_{x\rightarrow{\pi}}\dfrac{\mathrm{sen}(x)}{1-\cos(x)} $
$\displaystyle\lim_{x\rightarrow{0^+}}\dfrac{\ln (\mathrm{arcsen}(x))}{\cot(x)}$
$\displaystyle\lim_{x\rightarrow{0}}\dfrac{x}{\mathrm{arctg}(x)}$
${\displaystyle\lim_{x\rightarrow{+\infty}}}\left(\frac {\ 2\,}{\pi}\mathrm{arctg}(x)\right)^x$
${\displaystyle\lim_{x\rightarrow{+\infty}}}\left(\cos\left(\dfrac{2}{x}\right)\right)^{x^2}$
$\displaystyle\lim_{x\rightarrow{0^+}}\left(\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)\right)^x$
$\displaystyle\lim_{x\rightarrow{+\infty}}(\ln(x)-\ln(e^x+2))$
$\displaystyle\lim_{x\rightarrow{+\infty}}\dfrac{x^2}{\sqrt[3]{x^3+2}}$
$\displaystyle \lim_{x\to 0}\dfrac{\cos^2(x)-1}{e^{x^2}-1} =\lim_{x\to 0}\dfrac{-2\cos(x)\mathrm{sen}(x)}{e^{x^2}2x} =\lim_{x\to 0}\dfrac{-\mathrm{sen}(2x)}{2xe^{x^2}} =\lim_{x\to 0}\dfrac{-2\cos(2x)}{2e^{x^2}+4x^2e^{x^2}}=\frac{-2}{2+0}=-1$
$\displaystyle\lim_{x\rightarrow{(3\pi/2)^{+}}}(\sec(x)-\mathrm{tg}(x))=+\infty -(-\infty)=+\infty$
$\displaystyle\lim_{x\rightarrow{+\infty}}{\left(x^2-1\right)e^{-x^2}} =\lim_{x\rightarrow{+\infty}} \dfrac{x^2-1}{e^{x^2}} = \lim_{x\rightarrow{+\infty}} \frac{2x}{2xe^{x^2}}=\lim_{x\rightarrow{+\infty}} \frac{1}{e^{x^2}}=0$
$\displaystyle\lim_{x\rightarrow{+\infty}}\dfrac{\ln (\ln(x))}{\ln (x)} =\lim_{x\rightarrow{+\infty}}\dfrac{\dfrac{1}{x\ln(x)}}{\dfrac{1}{x}}=\lim_{x\rightarrow{+\infty}}\dfrac{1}{\ln(x)}=0$
$\displaystyle\lim_{x\rightarrow{\pi}}\dfrac{\mathrm{sen}(x)}{1-\cos(x)}=\frac{0}{1-(-1)}=0$
indeterminação do tipo $\frac{\infty}{\infty}$,podemos usar L'Hospital
\begin{eqnarray}\displaystyle\lim_{x\rightarrow{0^+}}\dfrac{\ln (\mathrm{arcsen}(x))}{\cot(x)} & = &\lim_{x\rightarrow{0^+}}\dfrac{ \frac{1}{\mathrm{arcsen}(x)\sqrt{1-x^2}}}{-\csc^2(x)} =\lim_{x\rightarrow{0^+}}-\dfrac{\mathrm{sen}^2(x)}{\mathrm{arcsen}(x)\sqrt{1-x^2}} =\lim_{x\rightarrow{0^+}}- \dfrac{\mathrm{sen}(2x)}{\frac{\sqrt{1-x^2}-x\mathrm{arcsen}(x)}{\sqrt{1-x^2}}} \\ & = &\lim_{x\rightarrow{0^+}}- \dfrac{\mathrm{sen}(2x)\sqrt{1-x^2}}{\sqrt{1-x^2}-x\mathrm{arcsen}(x)}=\frac{0}{1-0}=0\end{eqnarray}$\displaystyle\lim_{x\rightarrow{0}}\dfrac{x}{\mathrm{arctg}(x)} = \lim_{x\rightarrow{0}}\dfrac{1}{\frac{1}{1+x^2}} = \lim_{x\rightarrow{0}}1+x^2=1$
${\displaystyle\lim_{x\rightarrow{+\infty}}} \left(\frac {2}{\pi}\mathrm{arctg}(x)\right)^x = \displaystyle \lim_{x\rightarrow{+\infty}} e^{\ln\left(\frac {\ 2\,}{\pi}\mathrm{arctg}(x)\right)^x} = \lim_{x\rightarrow{+\infty}} e^{x\ln\left(\frac{2}{\pi}\mathrm{arctg}(x)\right)}$.
Vamos então calcular
\begin{eqnarray} \lim_{x\rightarrow{+\infty}} x\ln\left(\frac {2}{\pi}\mathrm{arctg}(x)\right) & = &\lim_{x\rightarrow{+\infty}}\dfrac{ \ln\left(\frac{2}{\pi}\mathrm{arctg}(x)\right)}{\frac{1}{x}} =\lim_{x\rightarrow{+\infty}}\dfrac{\dfrac{\frac{2}{\pi}\frac{1}{1+x^2}}{{\frac{2}{\pi}\mathrm{arctg}(x)}}}{-\dfrac{1}{x^2}} \\ & = & \lim_{x\rightarrow{+\infty}}\dfrac{\dfrac{1}{(1+x^2)\mathrm{arctg}(x)}}{-\dfrac{1}{x^2}}= \lim_{x\rightarrow{+\infty}}-\dfrac{x^2}{(1+x^2)\mathrm{arctg}(x)} \\ & = &\lim_{x\rightarrow{+\infty}}-\dfrac{x^2}{(1+x^2)}\dfrac{1}{\mathrm{arctg}(x)}=-\dfrac{2}{\pi}\end{eqnarray}Portanto $\displaystyle \lim_{x\rightarrow{+\infty}} e^{x\ln\left(\frac{2}{\pi}\mathrm{arctg}(x)\right)}=e^{-\frac{2}{\pi}}$
$\displaystyle\lim_{x\rightarrow{+\infty}}\left(\cos\left(\dfrac{2}{x}\right)\right)^{x^2} =\displaystyle \lim_{x\rightarrow{+\infty}} e^{\ln\left(\cos\left(\dfrac{2}{x}\right)\right)^{x^2}}=\lim_{x\rightarrow{+\infty}} e^{x^2\ln\left(\cos\left(\dfrac{2}{x}\right)\right)}$. Vamos então calcular
\begin{eqnarray}\lim_{x\rightarrow{+\infty}} x^2\ln\left(\cos\left(\dfrac{2}{x}\right)\right) & = & \lim_{x\to{+\infty}} \dfrac{\ln\left(\cos\left(\dfrac{2}{x}\right)\right)}{\dfrac{1}{x^2}} = \lim_{x\rightarrow{+\infty}} \dfrac{\dfrac{\frac{2}{x^2}\mathrm{sen}\left(\dfrac{2}{x}\right)}{\cos\left(\dfrac{2}{x}\right)}}{-\dfrac{2}{x^3}}=\lim_{x\rightarrow{+\infty}} -\dfrac{x\mathrm{sen}\left(\dfrac{2}{x}\right)}{\cos\left(\dfrac{2}{x}\right)} \\ & = & \lim_{x\rightarrow{+\infty}} -\dfrac{\mathrm{sen}\left(\dfrac{2}{x}\right)}{\dfrac{2}{x}}\dfrac{2}{\cos\left(\dfrac{2}{x}\right)}=-2.\end{eqnarray}Portanto $\displaystyle\lim_{x\rightarrow{+\infty}}\left(\cos\left(\dfrac{2}{x}\right)\right)^{x^2}=e^{-2}$.
$\displaystyle\lim_{x\rightarrow{0^+}}\left(\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)\right)^x =\displaystyle \lim_{x\rightarrow{0^+}}e^{x\ln\left(\mathrm{tg}\left(\dfrac{\pi} {x+2}\right)\right)}$. Vamos então calcular
\begin{eqnarray} \lim_{x\rightarrow{0^+}}x\ln\left(\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)\right) & = &\lim_{x\rightarrow{0^+}} \frac{\ln\left(\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)\right)}{\dfrac{1}{x}} =\lim_{x\rightarrow{0^+}} \dfrac{\dfrac{-\dfrac{\pi}{(x+2)^2}\sec^2\left(\dfrac{\pi}{x+2} \right)}{\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)}}{-\dfrac{1}{x^2}} \\ \\& = & \lim_{x\rightarrow{0^+}} \dfrac{-\dfrac{\pi}{(x+2)^2\mathrm{sen}\left(\dfrac{\pi}{x+2} \right)\cos\left(\dfrac{\pi}{x+2} \right)}}{-\dfrac{1}{x^2}}=\lim_{x\rightarrow{0^+}} \dfrac{\pi x^2}{(x+2)^2\mathrm{sen}\left(\dfrac{\pi}{x+2} \right)\cos\left(\dfrac{\pi}{x+2} \right)} \\ \\ & = & \lim_{x\rightarrow{0^+}} \dfrac{2\pi x^2}{(x+2)^2\mathrm{sen}\left(\dfrac{2\pi}{x+2} \right)} =\lim_{x\rightarrow{0^+}} \dfrac{4\pi x}{2(x+2)\mathrm{sen}\left(\dfrac{2\pi}{x+2} \right)-\cos\left(\dfrac{2\pi}{x+2}\right)}=\dfrac{0}{4\mathrm{sen}(\pi)-\cos(\pi)}=0\end{eqnarray}Então $\displaystyle\lim_{x\rightarrow{0^+}}\left(\mathrm{tg}\left(\dfrac{\pi}{x+2}\right)\right)^x=e^0=1$.
O $\displaystyle\lim_{x\rightarrow{+\infty}}(\ln(x)-\ln(e^x+2))$ tem uma indeterminação do tipo $\infty-\infty$ onde não podemos usar a regra de L'Hospital. Mas podemos aplicar a seguinte propriedade do logaritmo: $\ln(a)-\ln(b)=\ln\left(\dfrac{a}{b}\right)$. Então
$\displaystyle\lim_{x\rightarrow{+\infty}}(\ln(x)-\ln(e^x+2)) = \displaystyle\lim_{x\rightarrow{+\infty}}\ln\left(\frac{x}{e^x+2}\right)$. Mas $\displaystyle\lim_{x\rightarrow{+\infty}}\frac{x}{e^x+2} =\lim_{x\rightarrow{+\infty}}\frac{1}{e^x}=\lim_{x\rightarrow{+\infty}}e^{-x}=0$. Portanto, $\displaystyle\lim_{x\rightarrow{+\infty}}\ln\left(\frac{x}{e^x+2}\right)=\lim_{u\to 0^+}\ln\left(u\right)=-\infty$.
Este $\displaystyle\lim_{x\rightarrow{+\infty}}\dfrac{x^2}{\sqrt[3]{x^3+2}}$ apresenta uma indeterminação do tipo $\frac{\infty}{\infty}$, onde podemos aplicar a regra de L'Hospital. Tente calcular dessa forma! No entanto podemos também resolver como já fazíamos antes de aprender esta regra.
$$\displaystyle\lim_{x\rightarrow{+\infty}}\dfrac{x^2}{\sqrt[3]{x^3+2}}= \lim_{x\rightarrow{+\infty}}\sqrt[3]{\dfrac{x^6}{x^3+2}}=\lim_{x\rightarrow{+\infty}}\sqrt[3]{\dfrac{x^3}{1+\frac{2}{x^3}}}=+\infty$$
Nos exercícios abaixo encontre o valor de $a$ que satisfaz a igualdade.
$\displaystyle\lim_{x\rightarrow{+\infty}}\left(\frac{1+e^{2x}}{2}\right)^{\frac{a}{x}}=\sqrt{e}$
$\displaystyle\lim_{x\rightarrow{+\infty}}\left(\dfrac{x+a}{x-a}\right)^x=4$
$\displaystyle \lim_{x\rightarrow{+\infty}}\left(\dfrac{1+e^{2x}}{2}\right)^{\frac{a}{x}}=\lim_{x\rightarrow{+\infty}}e^{\frac{a}{x} \ln \left(\frac{1+e^{2x}}{2}\right)}$. Basta então verificar para qual valor de $a$ temos $\lim_{x\rightarrow{+\infty}} \frac{a}{x} \ln \left(\frac{1+e^{2x}}{2}\right)=\frac{1}{2}$.
$\displaystyle \lim_{x\rightarrow{+\infty}} \frac{a}{x} \ln \left(\frac{1+e^{2x}}{2}\right)=\lim_{x\rightarrow{+\infty}} \frac{a \ln \left(\frac{1+e^{2x}}{2}\right)}{x}= \lim_{x\rightarrow{+\infty}} \dfrac{ \frac{2ae^{2x}}{1+e^{2x}}}{1}= \lim_{x\rightarrow{+\infty}} \dfrac{2ae^{2x}}{1+e^{2x}}= \lim_{x\rightarrow{+\infty}} \dfrac{4ae^{2x}}{2e^{2x}}=2a$.
Portanto $2a=\frac{1}{2}$, logo $a=\frac{1}{4}$.
$\displaystyle\lim_{x\rightarrow{+\infty}}\left(\dfrac{x+a}{x-a}\right)^x=\lim_{x\rightarrow{+\infty}}e^{x\ln \left(\dfrac{x+a}{x-a}\right)}$. Como $4=e^{2\ln 2}$, basta então verificar para qual valor de $a$ temos $\displaystyle \lim_{x\rightarrow{+\infty}} x\ln \left(\dfrac{x+a}{x-a}\right)=2\ln 2$.
Mas $\displaystyle \lim_{x\rightarrow{+\infty}} x\ln \left(\dfrac{x+a}{x-a}\right)=\lim_{x\rightarrow{+\infty}} \dfrac{\ln \left(\frac{x+a}{x-a}\right)}{\frac{1}{x}}= \lim_{x\rightarrow{+\infty}} \dfrac{\frac{-2a}{x^2-a^2}}{\frac{-1}{x^2}}=\lim_{x\rightarrow{+\infty}} \dfrac{2ax^2}{x^2-a^2}=2a$, logo $a= \ln 2$.
Nos itens abaixo encontre, se existirem, as assíntotas horizontais e verticais do gráfico da função.
$f(x)=\dfrac{x}{\ln(x)}$
$f(x)=e^{\frac{1}{x}}$
$f(x)=x^2\ln(x)$
$f(x)=xe^{-x}$
$f(x)=\pi^{x^{3}}$ \hfill \ \
$\mathrm{D}$($f$)=$\left(0,1\right) \cup \left(1,+\infty\right)$
Assíntota vertical: $x=1$, pois $\displaystyle \lim_{x\to 1^{+}} \dfrac{x}{\ln(x)}=+\infty$ $\left( \text{e } \displaystyle \lim_{x\to 1^{-}} \dfrac{x}{\ln(x)}=-\infty\right)$.
Assíntotas horizontais não tem, pois $\displaystyle \lim_{x\to \pm\infty} \dfrac{x}{\ln(x)}= \lim_{x\to \pm\infty} \dfrac{1}{\frac{1}{x}}=\lim_{x\to \pm\infty} x=\pm \infty$$\mathrm{D}$($f$)=$\mathbb{R} \setminus \left\{0\right\}$
Assíntota vertical: $x=0$, pois $\displaystyle \lim_{x\to 0^+} e^{\frac{1}{x}}=+\infty$.
Assíntota horizontal: $y=1$, pois $\displaystyle \lim_{x\to \pm \infty} e^{\frac{1}{x}}=1$.$\mathrm{D}$($f$)=$\left( 0, +\infty\right)$
Assíntota vertical: não tem, pois $\displaystyle \lim_{x\to 0^+} x^2\ln(x)= \lim_{x\to 0^+} \frac{\ln(x)}{\frac{1}{x^2}}=\lim_{x\to 0^+} \frac{\frac{1}{x}}{-\frac{2}{x^3}}=\lim_{x\to 0^+} -x^2=0$.
Assíntota horizontal: não tem, pois $\displaystyle \lim_{x\to +\infty} x^2\ln(x)= +\infty$.$\mathrm{D}$($f$)=$\mathbb{R}$
Assíntota vertical: não tem.
Assíntota horizontal: $y=0$, $\displaystyle \lim_{x\to +\infty} xe^{-x}= \lim_{x\to +\infty} \dfrac{x}{e^{x}}= \lim_{x\to +\infty} \dfrac{1}{e^{x}}=0$.$\mathrm{D}$($f$)=$\mathbb{R}$
Assíntota vertical: não tem.
Assíntota horizontal: $y=0$, pois $\displaystyle \lim_{x\to -\infty} \pi^{x^{3}}=0$.
Seja $f: \mathbb{R} \to \mathbb{R}$ de classe $C^1$, tal que a reta tangente ao gráfico no ponto $(0,0)$ é $y=-x$. Calcule
$$\lim_{x \to 0} \dfrac{f(x)}{e^x-1}.$$Como $(0,0)$ é um ponto do gráfico de $f$ então $f(0)=0$ e a equação da reta tangente ao gráfico nesse ponto é $y=-x$, concluímos que $f'(0)=-1$. Assim, o limite pedido apresenta uma indeterminação do tipo $\frac{0}{0}$, logo podemos aplicar a Regra de L'Hospital:
$$\lim_{x \to 0} \dfrac{f(x)}{e^x-1}=\lim_{x \to 0} \dfrac{f'(x)}{e^x}=-1.$$

