Introdução às Derivadas
Em muitas situações pode ser bastante relevante aproximarmos uma função \(f\), a partir de um ponto \(x_0\), por um polinômio de grau 1. Lembrando que um polinômio de grau 1 tem como gráfico uma reta, isto significa que tentaremos aproximar o gráfico da função por uma reta. Entre algumas utilidades para esta aproximação podemos citar, por exemplo, saber se a função é crescente ou decrescente próximo ao ponto onde ela está sendo aproximada. Mas o que é uma boa aproximação?
Neste Applet, você pode movimentar livremente o ponto azul sobre o gráfico da função e, depois, movimentar o ponto vermelho para definir uma reta, isto é, uma função polinomial \(p\) de grau 1. Depois, movimente o ponto verde sobre o eixo x para calcular o erro da aproximação, isto é, a diferença entre \(p(x)\) e \(f(x)\).
Na primeira videoaula (Introdução às Derivadas - Parte 1), você verá que a melhor aproximação é aquela em que o erro, definido por \(erro(x) = p(x) - f(x)\), é tal que
\begin{equation}\lim_{x\to x_0} \frac{erro(x)}{x-x_0} = 0,\end{equation}ou seja,
\begin{equation}\lim_{x\to x_0} \frac{p(x)-f(x)}{x-x_0} = 0.\end{equation}Você verá também que, para que isto aconteça, o coeficiente angular \(a\) da reta é dado por
\begin{equation}a = \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}.\end{equation}Este número real é chamado de derivada da função \(f\) no ponto \(x_0\) e denotado por
$$f'(x_0)$$.
Assista o primeiro dos vídeos (Introdução às Derivadas - Parte 1) e à continuação leia a seção 1 do texto junto com os primeiros exercícios da lista.
No segundo vídeo (Introdução às derivadas - Parte 2), daremos uma interpretação geométrica para este valor. Repare que a razão \(\frac{f(x)-f(x_0)}{x-x_0}\) mede a inclinação da reta que passa pelos pontos \((x_0,f(x_0))\) e \((x,f(x))\), como no Applet abaixo. Aproxime \(x\) de \(x_0\), movendo o ponto vermelho, para ver o que acontece com a reta.
Esta reta estará se aproximando da reta tangente ao gráfico da função, no ponto \((x_0,f(x_0))\).
Assista o segundo vídeo (Introdução às derivadas - Parte 2) e depois ja pode ler o resto do texto e da lista de exercícios.
A Derivada como Aproximação
Nesse texto, queremos definir um conceito muito importante do cálculo: a derivada. Partimos da pergunta: dada uma função $f(x)$, é possível obter um polinômio de grau $1$, ou seja do tipo $p(x) = ax +b$, que seja uma boa aproximação para essa função? Muitas questões podem surgir dessa pergunta. Por que essa aproximação é útil? Só existe uma maneira de aproximar (se existir alguma)? O que é uma boa aproximação?
Podemos começar escrevendo:
$$f(x) \approx \underbrace{ax + b}_{p(x)}$$A Figura a seguir mostra os gráficos de uma função $f(x)$ e de algum polinômio de grau $1$, $p(x)$.
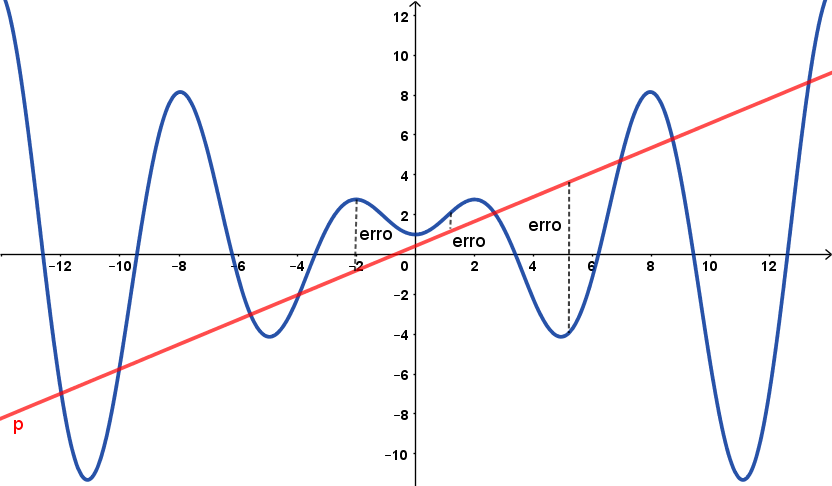
Note que para alguns valores de $x$, os gráficos de $f$ e $p$ estão próximos. Para outros valores, estão bem afastados. Queremos medir o quão próximo $f$ e $p$ estão, calculando a diferença $f(x) - p(x)$. Essa diferença será entendida como o erro da nossa aproximação. Esse erro depende do ponto $x$ e definimos uma funçao $erro(x)= f(x) - p(x)$.
Seja $f(x)= -x^3 + 2x$, e considere $p(x) = -x$. O gráfico dessas funçoes está representado na Figura abaixo:
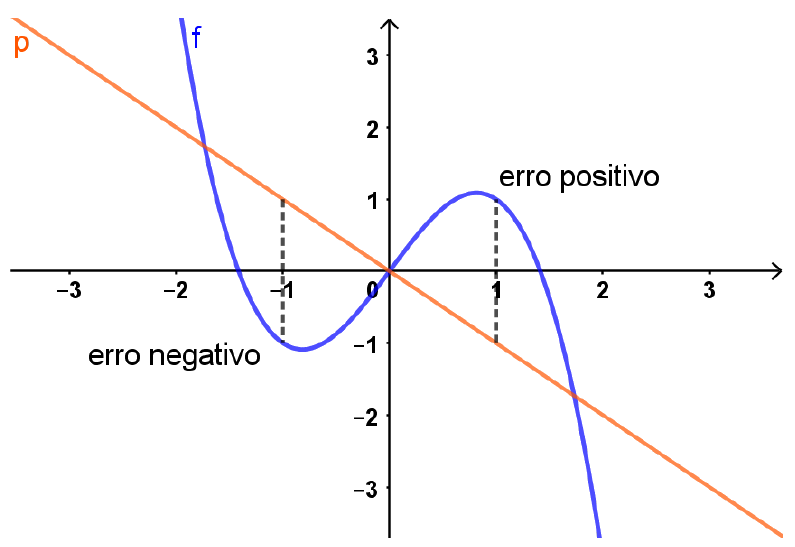
O erro pode ser positivo ou negativo.
Em $x = -1$, podemos calcular o erro como $erro(-1) = f(-1) - p(-1) = -1-1 = -2$. Em $x= 0$, temos $erro(0) = 0$.
Considere $f(x) = x^2 -x$ e $p(x) = x+1$. Se $p(x)$ fosse sugerido para aproximar $f$, qual seria a expressão do $erro(x)$? Em que pontos a aproximação seria exata ($erro = 0$)? Quanto vale $erro(0)$?
$erro(x) = x^2 - 2x -1$, a expressão é exata em $x = 1 + \sqrt{2}$ e $x= 1-\sqrt{2}$, em $x=0$, $erro(0) = -1$.
Faça o gráfico das funçãos $f$ e $p$ do Exemplo 1 e interprete seu resultado geometricamente.
Para uma função arbitrária, é improvável que uma única reta forneça uma aproximaçao razoável em todo valor de $x$. Vamos fixar algum ponto $x_0$, no domínio de $f$, e tentar procurar uma aproximação que seja boa em algum intervalo em torno desse valor. Vamos exigir que a aproximação seja exata em $x_0$, isto é: $erro(x_0)=0$. Além disso, como queremos uma boa aproximação "perto" de $x_0$, vamos exigir que $\lim_{x\rightarrow x_0} erro(x) =0$. Observe que essa última exigência implica na continuidade de $erro(x)$ em $x_0$.
Reescrevemos nosso problema como segue. Seja $x_0$ um ponto do domínio de $f$. Procuramos $a$ e $b$ tais que
$\begin{cases} f(x) = ax + b + erro(x),\\ \\ erro(x_0) = 0, \\ \\ \lim_{x \rightarrow x_0}erro(x) = 0. \end{cases} $
Como $erro(x_0) = 0$, temos $f(x_0) = ax_0 + b$ e, portanto, $b= f(x_0) - ax_0$. Substituindo esse valor de $b$ na expressão de $f$, obtemos: $f(x) = ax + f(x_0) - ax_0 + erro(x)$. Reescrevendo, temos o problema de determinar $a$ tal que:
\begin{equation}\tag{1}f(x) = f(x_0) + a(x-x_0) + erro(x).\end{equation}Geometricamente, teremos alguma reta contendo o ponto $(x_0,f(x_0))$ como na Figura abaixo:

A aproximaçao é exata em um ponto.
A questão, agora, é determinar qual, dentre as retas que satisfazem essas condições, vamos escolher. Note, na Figura 1, que várias retas poderiam servir. Em todas elas, o erro tende a $0$. O que as diferencia é a velocidade com que esse erro tenderá a $0$.
Olhando para a expressão 1 e tomando o limite dos dois lados:
$$\lim_{x \rightarrow x_0} f(x) = f(x_0) + \cancelto{0}{a(x-x_0)} + \cancelto{0} {erro(x)}.$$Vemos que, perto de $x_0$, $f$ está sendo aproximada por $f(x_0)$ mais a soma de dois termos, cada um deles tendendo a $0$. A pergunta chave, aqui, é: perto de $x_0$, qual dos dois termos será mais relevante? Será que, na medida que nos aproximamos de $x_0$, o valor da expressão que aproxima $f$ será mais próximo de $f(x_0) + a(x-x_0)$ ou de $f(x_0) + erro(x)$? Bem, isso depende da velocidade relativa com que $a(x-x_0)$ e $erro(x)$ estão se aproximando de $0$. Se $a(x-x_0)$ for a $0$ muito mais rápido que o $erro$, quanto mais perto $x$ estiver de $x_0$, mais o termo $erro(x)$ será relevante na aproximação e mais $a(x-x_0)$ será desprezível. Na verdade, perto de $x_0$, estaríamos usando $f(x_0) + \cancel{a(x-x_0)} + erro(x)$ para aproximar $f$, uma vez que o termo linear seria desprezível perto de $erro(x)$. Mas, isso é exatamente o que não queremos!!! Começamos o problema, buscando uma aproximaçao de grau $1$. Então é razoável pedir que $erro(x)$ tenda a $0$ mais rápido que $a(x-x_0)$, quando $x \rightarrow x_0$.
Como comparar a velocidade com que duas funçãos vão para $0$? Imagine que você tem uma quantidade de dinheiro que depende do tempo, $din(t)$, e quer distribuir esse dinheiro por uma quantidade (que também depende do tempo) de pessoas, $pess(t)$. A cada tempo $t$, cada pessoa vai receber $\frac{din(t)}{pess(t)}$ reais. Suponha que, com o passar do tempo, o dinheiro comece a diminuir (tendendo a zero) e o número de pessoas também vá diminuindo. Quanto cada uma vai receber? Se o dinheiro diminuir muito mais rápido, a tendência é que cada pessoa receba cada vez menos. Isso é $\frac{din(t)}{pess(t)}$ vai tender a zero. Por outro lado, se o núumero de pessoas diminuir muito mais rápido que o dinheiro, a tendência é que cada uma delas receba cada vez mais com o passar do tempo; isto é: $\frac{din(t)}{pess(t)}$ tende a infinito. Se o dinheiro e o número de pessoas diminuir na mesma proporção, a quantidade de dinheiro que cabe a cada uma tenderá a se manter constante. Esse raciocínio natural torna razoável uma definição mais formal para compararmos a velocidade com que duas funçãos tendem a zero.
Suponha que $f$ e $g$ são duas funçãos com domínio e contradomínio real e suponha $\displaystyle \lim_{x \rightarrow x_0} f(x) = \lim_{x \rightarrow x_0} g(x) = 0$.
Se $\displaystyle \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)}= 0$, dizemos que $f$ tende a zero mais rápido que $g$, em uma vizinhança de $x_0$.
Se $\displaystyle \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)}= \infty $, dizemos que $g$ tende a zero mais rápido que $f$, em uma vizinhança de $x_0$.
Se $\displaystyle \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)}= K $, $K$ constante, $K \neq 0$, dizemos que $f$ e $g$ tendem a zero com a mesma velocidade.
Sejam $f(x) = x^2 $ e $g(x) = x^{1/3}$. Para saber quem tende a zero mais rápido, olhamos o $\displaystyle \lim_{x \rightarrow 0} \frac{x^2}{x^{1/3}}$. Como o limite é zero, dizemos que $x^2$ tende a zero mais rápido que $x^{1/3}$, na vizinhança de $x=0$. A Figura ??? mostra o desenho das duas funções. Não é difícil ver que, muito próximo de $x = 0$, $x^2$ é substancialmente menor que $x^{1/3}$.
Estamos lançando mão aqui de um conceito muito usado em cálculo numérico, conhecido como ordem de convergência frequentemente denotado por $\cal{O}$.

Comparando a velocidade de convergência de $x^2$ e $x^{1/3}$
Na nossa aproximaçao queremos que $erro(x)$ tenda a zero mais rápido que $a(x-x_0)$. Então, o problema passa a ser formulado assim: procuramos determinar $a$, tal que:
\begin{equation}\tag{2}\begin{cases} f(x) = f(x_0) + a(x-x_0) + erro(x),\\ \\ erro(x_0) = 0, \\ \\ \displaystyle\lim_{x \rightarrow x_0}\frac{erro(x)}{x-x_0} = 0. \end{cases} \end{equation}
Vale observar que, no problema formulado em 2, $f$ é necessariamente contínua se a aproximaçao existir. As condiçoes sobre $erro(x)$, garantem essa continuidade. Tente fazer o exercício a seguir (antes de ver a solução).
Mostre que se existe $a$ que satisfaz o problema 2, $f$ é contínua em $x_0$.
Como $\\lim_{x \rightarrow x_0}\frac{erro(x)}{x-x_0} = 0$, podemos concluir que $\lim_{x \rightarrow x_0} erro(x) = 0 = erro(x_0)$. Portanto $erro(x)$ é uma função contínua em $x_0$; logo, $f$ é contínua em $x_0$ por ser a soma de funções contínuas em $x_0$.
Suponha, agora, que existe um $a$ que satisfaz o problema 2. A funçao $f$ será dita diferenciável (ou derivável) em $x_0$ e o valor de $a$ será chamado de derivada de $f$ em $x_0$, e comumente denotado por $f'(x_0)$.
Pensando dessa maneira, a derivada é um determinado valor que serve para construir uma aproximaçao de grau $1$, com características bem determinadas, para a função. Esse conceito é um tanto abstrato e seria natural perguntar: como calcular esse valor? Quando a derivada em um ponto existe (isto é, a aproximaçao que satisfaz 2 existe) só tem um valor? Ou poderíamos encontrar mais de um valor para $a$?
Essas perguntas podem ser respondidas com alguns algebrismos. Nas contas seguintes, vamos supor que $a$ existe e, de acordo com a nossa definição/notaçao de derivada, vamos substituir o símbolo $a$ por $f'(x_0)$. Se $f$ é diferenciável em $x_0$:
$$\begin{align*} f(x) = f(x_0) + f'(x_0)(x-x_0) + erro(x) &\Longleftrightarrow f(x) - f(x_0) = f'(x_0) (x-x_0) + erro(x),\\ \\&\Longleftrightarrow \dfrac{f(x) -f(x_0)}{(x-x_0)} = f'(x_0) + \dfrac{erro(x)}{x-x_0}. \end{align*} $$
Tomando o $\lim_{x \rightarrow x_0}$ dos dois lados, temos:
\begin{equation}\displaystyle \lim_{x \rightarrow x_0}\frac{f(x) -f(x_0)}{x-x_0} = f'(x_0) + \lim_{x \rightarrow x_0}\frac{erro(x)}{x-x_0}.\end{equation}E como $\displaystyle \lim_{x \rightarrow x_0}\frac{erro(x)}{x-x_0} = 0$, obtemos explicitamente uma expressão para $f'(x_0)$:
\begin{equation}\tag{3}\displaystyle f'(x_0) = \lim_{x \rightarrow x_0}\frac{f(x) -f(x_0)}{x-x_0}.\end{equation}Observe que, se o limite em 3 existir, já sabemos que é único. O que responde a nossa pergunta sobre quantas aproximaçoes poderemos ter. De fato, só teremos uma.
Podemos, refrasear nossa definiçao de derivada por uma definiçao equivalente dizendo que:
Se existir o limite em 3, dizemos que $f$ é diferenciável (ou derivável) em $x_0$ e que sua derivada (comumente denotada por $f'(x_0)$) é o valor desse limite:
\begin{equation}\tag{4}\displaystyle f'(x_0) = \lim_{x \rightarrow x_0}\frac{f(x) -f(x_0)}{(x-x_0)}.\end{equation}Uma outra notaçao bastante comum para derivada é: $\displaystyle\frac{dy}{dx}(x_0)$.
É comum escrever a razão na equação 4 como:
$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x_0+h) - f(x_0)}{h}.$$
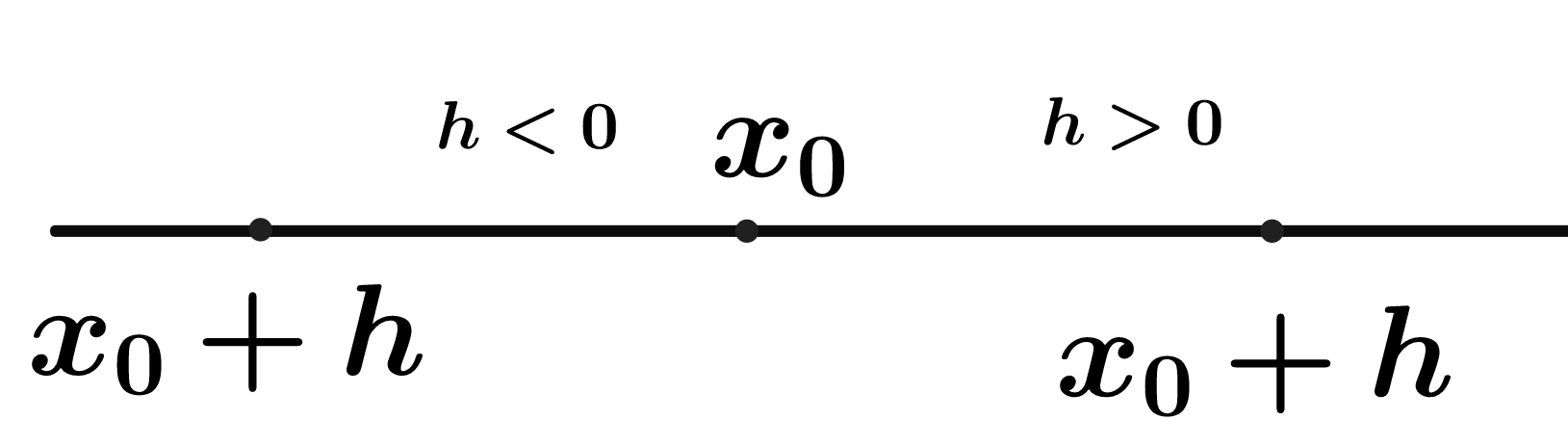
Mudança de variável $x = x_0 +h$.
Nesse caso, imaginamos que existe uma variável $h$ e que $x= x_0 + h$ como na Figura 3. Para que $x$ tenda a $x_0$, tomamos o limite quando $h$ tende a $0$.
Nessa seçao tentamos construir o conceito de derivada buscando aproximar uma função por um polinômio. Nos tópicos seguintes, vamos trabalhar geométrica e fisicamente com a noçao de derivada.
Algumas questões para pensar (serão tratadas nas próximas seções, mas seria interessante tentar respondê-las antes de seguir adiante).
Se $f$ tem derivada em um ponto, aproximamos $f$ pelo polinômio $p(x) = f(x_0) + f'(x_0) (x-x_0)$, cujo gráfico é uma reta. Como essa reta e o gráfico de $f$ se relacionam?
Comece verificando que essa reta contém (como era de se imaginar) o ponto $(x_0, f(x_0))$ e o coeficiente angular dela é $f'(x_0)$. O que será que esse coeficiente angular nos conta? Lembre que é um limite. Desenhe uma curva qualquer, fixe um ponto $(x_0, f(x_0))$. Escolhendo valores de $x$ próximos desse ponto, tente dar um significado geométrico para $\frac{f(x) -f(x_0)}{(x-x_0)}$. Quando $x$ tender para $x_0$, qual reta terá esse coeficiente?
Imagine que $f$ representa a posiçao de um objeto em movimento. Qual o significado físico de $\displaystyle \frac{f(x) -f(x_0)}{(x-x_0)}$?
E se $f$ representar a velocidade de um objeto em movimento?
Discutiremos essas e outras questõoes nos próximos tópicos. Também começaremos a ver, na prática, como derivadas são calculadas.

