O Polinômio de Taylor
Já vimos que a derivada em um ponto $x_0$ permite uma aproximação polinomial de grau $1$ de uma função $f$, na forma:
\begin{equation}f(x) = f(x_0) + f'(x_0)(x-x_0) + erro(x) \mbox{ e } \tag{1}\end{equation} \begin{equation}\lim_{x \to x_0} \frac{erro(x)}{x-x_0} = 0 \tag{2}\end{equation}Vimos também que, sendo a derivada única, $f'(x_0)$ é a única constante que pode ser usada como coeficiente angular de forma a obter as equações 1 e 2, considerando que o $erro$ é a diferença entre $f$ e a aproximação afim. É natural nos perguntarmos o que aconteceria se quiséssemos uma aproximação de grau $2$ (ou maior) em uma vizinhança de $x_0$. Isto é, poderíamos perguntar: será que existem $a_1$ e $a_2$ tais que:
\begin{equation}\tag{3}f(x) = f(x_0) + a_1(x-x_0) + a_2 {(x-x_0)}^2 + erro(x) \mbox{?}\end{equation}A próxima seção é dedicada a estudar essa aproximação. Na primeira parte, construímos a dedução da aproximação (ou algo muito perto disso); na segunda, discutimos algumas propriedades e aplicações. A primeira parte (dedução) envolve detalhes bastante técnicos. Sendo esse um primeiro curso de cálculo, o aluno que não se sentir à vontade em acompanhar tantos detalhes, pode perfeitamente pular a primeira parte (a dedução) e, acreditando que a aproximação existe, passar à subseção dedicada às aplicações e considerações gerais.
Justificativa da Fórmula (quase uma dedução)
Vamos supor que existe alguma aproximação como na equação 3. Se substituirmos $x$ por $x_0$ na equação teremos $f(x_0) = f(x_0) + erro(x_0)$ de onde concluímos que, se a aproximação existir, $erro (x_0) = 0$.
De modo análogo ao que procedemos na definição de derivada, queremos que $erro(x)$ vá a $0$ mais rápido que ${(x-x_0)}^2$ para que, perto de $x_0$, a parte quadrática do polinômio sobressaia sobre o $erro(x)$. Isso significa, a exemplo do que fizemos na definição de derivada, que estamos impondo a condição:
\begin{equation}\tag{4}\lim_{x \to x_0} \frac{erro(x)}{(x-x_0)^2} = 0\end{equation}Observe que a equação 4 implica, também, que $erro'(x_0) = 0$. De fato,
\[erro'(x_0) = \lim_{x \to x_0} \frac{erro(x)-erro(x_0)}{x-x_0}\]e, como $erro(x_0) = 0$, temos:
\[erro'(x_0) = \lim_{x \to x_0} \frac{erro(x)}{x-x_0}\]Mas, como estamos supondo que
$$\lim_{x \to x_0} \frac{erro(x)}{(x-x_0)^2} = 0$$podemos escrever:
\begin{eqnarray}0 \leq |erro'(x_0)| = \left| \lim_{x \to x_0} \frac{erro(x)}{x-x_0}\right|\leq \left|\lim_{x \to x_0} \frac{erro(x)}{(x-x_0)^2}\right| = 0\end{eqnarray}Então, nosso problema completo é verificar quais seriam as constantes $a_1$ e $a_2$ que poderiam nos levar a essa aproximação. Vamos admitir que $f$ pode ser derivada quantas vezes desejarmos em algum intervalo contendo $x_0$. Derivando a equação 3 uma vez, temos:
\begin{equation}\tag{5}f'(x) = a_1 + 2a_2 (x-x_0) + erro'(x).\end{equation}Avaliando a equação 5 em $x=x_0$ e lembrando que $erro'(x_0) = 0$ obtemos:
\begin{equation}\tag{6}f'(x_0) = a_1\end{equation}De onde sabemos que $a_1$ deve ser a derivada de $f$ em $x_0$. Com essa informação, reescrevemos 5 como:
\begin{equation}f'(x) = f'(x_0) + 2a_2 (x-x_0) + erro'(x)\end{equation}Passando $f'(x_0)$ para o lado esquerdo da igualdade e dividindo os dois lados por $(x-x_0)$ temos:
\begin{equation}\tag{7}\frac{f'(x) - f'(x_0)}{x-x_0} = 2a_2 + \frac{erro'(x)}{(x-x_0)} \\\end{equation}.
Tomando $\lim_{x \to x_0}$ dos dois lados da equação, vem:
\begin{equation}\tag{8}\lim_{x \to x_0}\frac{f'(x) - f'(x_0)}{x-x_0} = \lim_{x \to x_0} 2a_2 + \cancelto{0}{\lim_{x \to x_0}\frac{erro'(x)}{(x-x_0)}}\end{equation}Na equação 8 usamos que:
\[\lim_{x \to x_0}\frac{erro'(x)}{(x-x_0)} = \lim_{x \to x_0}\frac{\frac{erro(x) - erro(x_0)}{(x-x_0)}}{x-x_0} = \lim_{x \to x_0}\frac{erro(x) }{(x-x_0)^2}\]Da equação 8 concluímos que
$$2a_2 = f''(x_0).$$Reescrevemos as equações 3 e 4 como
\begin{equation}\tag{9}f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f^{(2)}(x_0)}{2} {(x-x_0)}^2 + erro(x)\end{equation} \begin{equation}\tag{10}\lim_{x \to x_0}\frac{erro(x)}{(x-x_0)^2} = 0\end{equation}Concluímos que, se for possível escrever $f(x)$ como uma aproximação polinomial de grau $2$ na forma da equação 3 com o erro se aproximando de $0$ mais rápido que $(x-x_0)^2$ quando $x \to x_0$, $a_1$ deve ser $f'(x_0)$ e $a_2$ deve ser $\frac{f''(x_0)}{2}$.
Poderíamos repetir o procedimento, buscando uma aproximação de grau 3 da forma:
\[f(x) = f(x_0) + a_1(x-x_0) + a_2(x-x_0)^2 + a_3 (x-x_0)^3 + erro(x)\]Supondo que essa aproximação exista, que $f$ seja de classe $C^4(I)$ - onde $I$ é algum intervalo em torno de $x_0$ - chegaríamos à conclusão que $a_3$ estaria relacionado com a terceira derivada de $f$; mais precisamente, $a_3 = \frac{f^{'''}(x_0)}{3!}$ (em que o símbolo ``$!$'' representa fatorial).
O polinômio de Taylor, aplicações e considerações gerais
Na seção anterior justificamos o Teorema a seguir:
Se $f$ tiver $n+1$ derivadas em algum intervalo $I$ contendo $x_0$ (em particular isso implica que $f \in C^n(I)$) então, é possível fazer a aproximação polinomial
\begin{equation}\tag{11}f(x) = f(x_0) + f'(x_0) (x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \frac{f^{'''}(x_0)}{3!}(x-x_0)^3 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + erro(x)\end{equation}em que $\lim_{x \to x_0} \frac{erro(x)}{(x-x_0)^{n}} = 0$.
O polinômio:
\begin{equation}\tag{12}P(x) = f(x_0) + f'(x_0) (x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \frac{f^{(3)}(x_0)}{3!}(x-x_0)^3 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\end{equation}é conhecido como polinômio de Taylor de ordem (ou grau) $n$ da função $f$ e é muito usado para aproximar funções. Existem várias fórmulas para o $erro$ (diferença entre $f(x)$ e $P(x)$). Uma estimativa muito usada é conhecida como fórmula de Lagrange, que colocamos no teorema a seguir.
Nas mesmas hipóteses do Teorema 1, existe um $c$ entre $x_0$ e $x$ ($x<c<x_0$ ou $x_0 < c < x$) tal que:
\begin{equation}\tag{13}erro(x) = \frac{f^{(n+1)}(c)}{(n+1)!} (x-x_0)^{n+1}\end{equation}Mais uma vez, se explicita que o erro tende a zero mais rápido que $(x-x_0)^n$, o que significa que, quanto maior o $n$ ou, equivalentemente, quanto mais vezes você puder derivar a função, menor será o erro da aproximação no limite quando $x\to x_0$. Vale ressaltar que o fato do erro ser pequeno, no limite, para $n$ grande, diz que a aproximação é boa em algum intervalo em torno de $x_0$. Todavia, o tamanho desse intervalo depende muito das características particulares da função que está sendo aproximada. Muitas vezes, o intervalo em que essa aproximação é boa é bastante pequeno. Além disso, é possível que tenhamos que tomar $n$ muito grande para conseguir uma boa aproximação.
As figuras ??? e ??? exibem em vermelho o gráfico de $\cos(10x)$ e, em azul, os gráficos de polinômios de Taylor (de ordem $3$ e $10$, respectivamente) de $\cos(10x)$. Nas figuras ??? e ??? estão os gráficos de $\cos(x)$ em vermelho e, em azul, as aproximações de ordem $3$ e $10$, respectivamente. Vamos comparar os intervalos em que as aproximações têm erros pequenos. Note que a amplitude do intervalo (em torno de $0$) em que as aproximações são boas, é muito maior na função $\cos(x)$ do que na função $\cos(10x)$. Ambas as funções são de classe $C^{\infty} (\mathbb{R})$. O que faz com que o tamanho desses intervalos varie tanto é a presença de "picos mais íngremes" no gráfico de $\cos(10x)$. Essa noção pode ser formalizada com um conceito conhecido como módulo de continuidade de uma função. Aqui, estamos apenas exemplificando.
Grosso modo, o módulo de continuidade de $f$ em um intervalo $[a,b]$ é dado pela variação máxima de $f$ quando $[a,b]$ é particionado em subintervalos, cada vez menores.
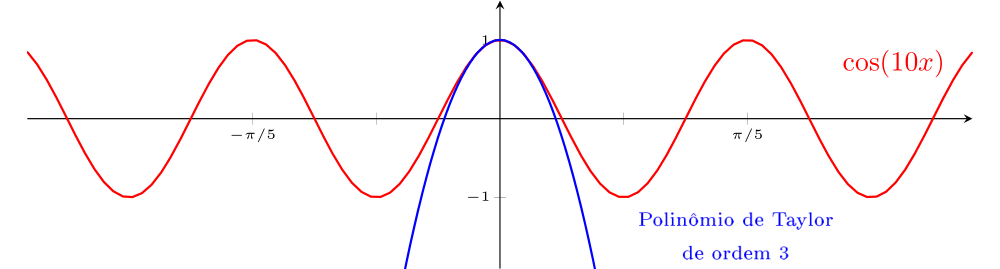
$\cos(10x)$ em vermelho e sua aproximação pelo polinômio de Taylor de ordem $3$ (em azul).
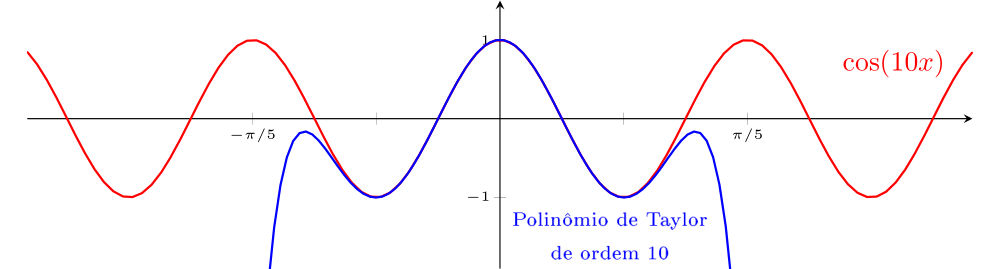
$\cos(10x)$ em vermelho e sua aproximação pelo polinômio de Taylor de ordem $10$ (em azul).
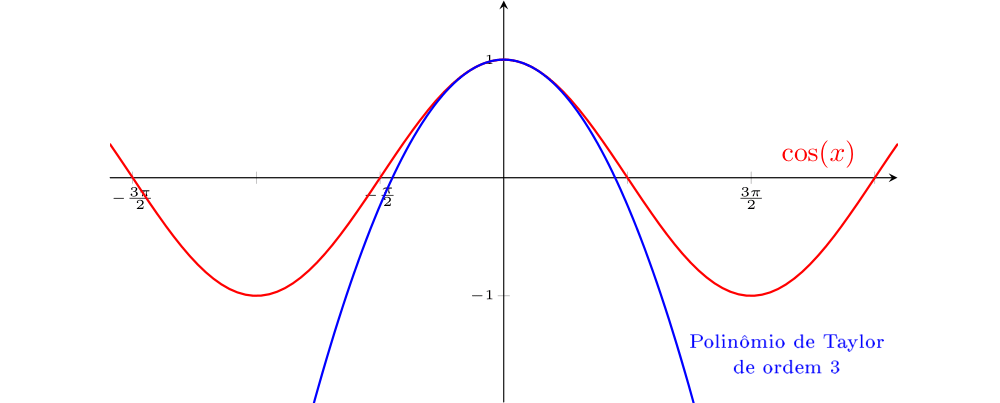
$\cos(x)$ em vermelho e sua aproximação pelo polinômio de Taylor de ordem $3$ (em azul).
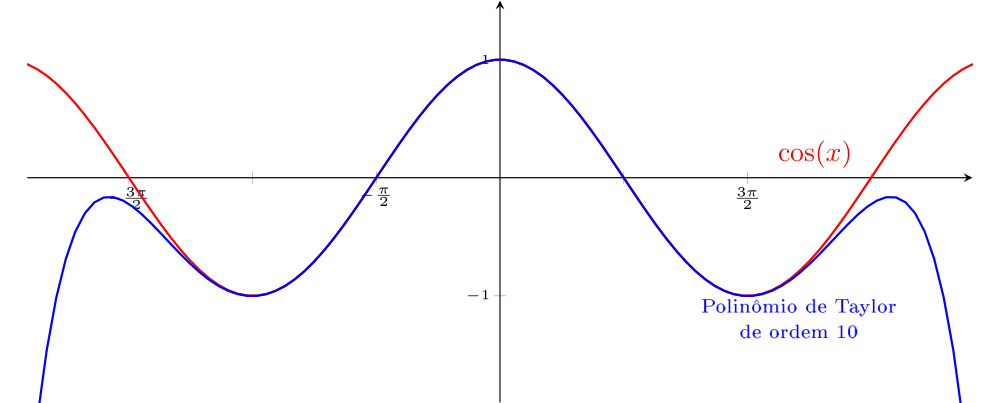
$\cos(x)$ em vermelho e sua aproximação pelo polinômio de Taylor de ordem $8$ (em azul).
Frequentemente, o polinômio de Taylor de ordem $n$ da função $f$, em torno de $x_0$, é escrito como:
\begin{equation}\tag{14}\sum_{j=0}^n \frac{f^{(j)}(x_0)}{j!}(x-x_0)^j\end{equation}Quando se considera o $\lim_{n \to \infty} \sum_{j=0}^n \frac{f^{j}(x_0)}{j!}(x-x_0)^j$ obtemos uma soma infinita, conhecida como série de Taylor da função.
Para calcularmos o polinômio de Taylor de grau $n$, em torno de $x_0$, de uma função, precisamos determinar suas derivadas em $x_0$. Nos próximos exemplos, calculamos alguns casos bem conhecidos.
Obtenha o polinômio de Taylor de grau 6, em torno de $x_0=0$, de $f(x) = e^x$.
Vamos calcular as derivadas de ordem $n$ de $e^x$, para $n = 1,2, \ldots, 6$. No caso da exponencial, temos que $e^x = f^{(0)}(x)= f^{(1)}(x) = f^{(2)}(x) = \cdots = f^{(6)}(x)$. Como estamos calculando em torno de $x_0=0$, vamos avaliar cada uma das derivadas em $x=0$. Como todas as derivadas valem $e^x$, temos, $f^{(n)}(x)|_{x=0} = e^x|_{x=0} =1$. Usando a equação 12 temos o polinômio de Taylor da exponencial:
\begin{eqnarray}\tag{15}e^x & \approx f(x_0) + f'(x_0) (x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \frac{f^{'''}(x_0)}{3!}(x-x_0)^3 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\\ \\& = 1+ x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!}\end{eqnarray}Observe que se tomarmos infinitos termos na expressão polinomial, (admitindo que, nesse caso, o erro seja $0$, o que é verdade mas não provamos) obteremos:
\[e^x = 1+ x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!} + \cdots\]derivando dos dois lados:
\[\begin{array}{lll}(e^x)' & = & \left( 1+ x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!} + \cdots\right)'\\& & \\& = & 1+ x + \frac{x^2}{2} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \frac{x^6}{6!} + \cdots\end{array}\]Ao derivarmos a expressão, obtemos a própria expressão, o que é compatível com o fato da função exponencial ter por derivada ela mesma.
Obtenha o polinômio de Taylor de ordem $6$, em torno de $x_0 = 0$ da função $f(x) = \cos(x)$.
Para usar a fórmula, precisamos calcular as derivadas de $\cos(x)$ até ordem $6$ e avaliar em $x=0$. Fazemos isso na tabela a seguir:
| {$n$} | $f^{(n)}(x)$ | $f^{(n)}(0)$ |
| $0$ | $\cos(x)$ | $1$ |
| $1$ | $-\mathrm{sen}(x)$ | $0$ |
| $2$ | $-\cos(x)$ | $-1$ |
| $3$ | $\mathrm{sen}(x)$ | $0$ |
| $4$ | $\cos(x)$ | $1$ |
| $ 5$ | $-\mathrm{sen}(x)$ | $0$ |
| $6$ | $-\cos(x)$ | $ -1$ |
Usando os cálculos da tabela, e usando que $f(x) = \cos(x)$ escrevemos:
\begin{eqnarray}\tag{16}\cos(x) & \approx f(x_0) + f'(x_0) (x-x_0) + \frac{f''(x_0)}{2!} (x-x_0)^2 + \frac{f^{'''}(x_0)}{3!}(x-x_0)^3 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \\ \\& = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!}\end{eqnarray}Observe que o polinômio encontrado é uma função par, assim como a função cosseno.
Calcule $\lim_{x \to 0}\frac{\cos(x) - 1}{x}$.
Sabemos que, no limite, o polinômio de Taylor aproxima $\cos(x)$. Usando o exemplo anterior, escrevemos:
\[\begin{array}{lll}\lim_{x \to 0}\frac{\cos(x) -1}{x} & = & \lim_{x \to 0}\frac{1}{x} \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots + \frac{x^{2n}}{(2n)!} +erro(x) - 1\right) \\ \\& = & \lim_{x \to 0}\frac{1}{x} \left( \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots +\frac{x^{2n}}{(2n)!} +erro(x)\right) \\ \\& = & \lim_{x \to 0} \left(\frac{x}{2!} + \frac{x^3}{4!} - \frac{x^5}{6!} + \cdots + \frac{x^{2n-1}}{(2n)!} + \frac{erro(x)}{x} \right) \\ \\& = & 0\end{array}\]Várias manipulações algébricas podem ser feitas com polinômios de Taylor. Por exemplo, se a função cujo polinômio estamos calculando puder ser derivada $n$ vezes perto de $x_0$, o polinômio de Taylor de ordem $n-1$ da derivada pode ser obtido derivando o polinômio de Talor da função, como no exemplo a seguir.
Obtenha o polinômio de Taylor de ordem $5$ de $f(x) = \mathrm{sen}(x)$.
Vamos proceder derivando o polinômio de Taylor de $g(x) = -\cos(x)$. Temos:
\[-\cos(x) \approx -1 + \frac{x^2}{2!} - \frac{x^4}{4!} + \frac{x^6}{6!}\]Derivando os dois lados da equação, temos o polinômio de Taylor de ordem $5$ de $\mathrm{sen}(x)$:
\[\mathrm{sen}(x) \approx x - \frac{x^3}{3!} + \frac{x^5}{5!}\]Listamos a seguir aproximações muito usadas, provenientes de cálculos de polinômios de Taylor, todas em torno de $x_0=0$. Nessa lista, em que todas as funções são de classe $C^{\infty}$ nos seus domínios não estabelecemos a ordem do polinômio, uma vez que podemos aumentar $n$ tanto quanto quisermos:
\[\begin{array}{llll}e^x & \approx & 1 + x +\frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots + \dfrac{x^n}{n!} & n = 0,1,2,3 \ldots \\\cos(x) & \approx & 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots + \dfrac{(-1)^n x^{2n}}{(2n)!} & n = 0,1,2,3 \ldots\\\mathrm{sen}(x) & \approx & x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + \dfrac{(-1)^nx^{2n+1}}{(2n+1)!} & n =0, 1,2,3, \ldots \\\ln(1+x) & \approx & x -\frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4}+ \frac{x^5}{5} + \cdots + \dfrac{(-1)^{n} x^{n+1}}{n+1} & n = 0, 1,2,3 \ldots \\\end{array}\]Observe que no caso do $\ln(1+x)$, $x$ varia em torno de $0$, de modo que $\ln(1+x)$ está variando em torno de $\ln(1)$. Vamos resolver mais alguns exemplos usando as aproximações dessa lista.
Vamos considerar o polinômio de Taylor de ordem $5$ para $e^x$ no ponto $x=1$.
\[e \approx 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!}\]Com que precisão, esse polinômio aproxima o número $e$?
Sabemos que o erro máximo é dado por $\frac{f^{(n+1)}(c)}{(n+1)!} $ para algum $c$ entre $0$ e $1$. No caso da exponencial, ${f^{(n+1)}(c) = e^c}$ e como $c \in (0,1)$ estimamos o valor máximo para a derivada como $e^1 <3$. Portanto podemos escrever:
\begin{equation}\tag{17}0 < \left|e -\left( 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!}\right)\right| \leq \frac{3}{6!}\end{equation}Usando um polinômio de ordem $n$, escrevemos:
\begin{equation}\tag{18}0 \leq \left|e -\left( 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} + \cdots + \frac{1}{n!}\right)\right| \leq \frac{3}{(n+1)!}\end{equation}Usando o Teorema do confronto (tomando $ \lim_{n \to \infty}$) na equação 18 podemos escrever uma igualdade:
\[e = \sum_{n=0}^\infty \frac{1}{n!}\]Isso permite descrever o número $e$ como limite de uma soma.
Calcule um valor aproximado para a soma:
\[1 + 2 + \frac{2^2}{2!} + \frac{2^3}{3!} + \frac{2^4}{4!} + \frac{2^5}{5!}\]olhando a expressão, vemos que ela é um polinômio de Taylor de $e^x$ em $x=2$. Portanto, podemos tomar $e^2$ como valor aproximado da expressão.
Quanto vale $ \lim_{x \to 0}\frac{\mathrm{sen}(x)}{x}$?
A aproximação do seno é:
\[x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + \dfrac{(-1)^n x^{2n+1}}{(2n+1)!}\]Podemos dividir essa aproximação por $x$ para obter:
\[\frac{\mathrm{sen}(x)}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} -\frac{x^6}{7!}+ \cdots \dfrac{(-1)^n x^{2n+1}}{(2n+1)!} + \dfrac{erro(x)}{x}\]Note que, se tomarmos o limite quando $x \to 0$ da aproximação, ela tende a $1$, como deveria acontecer. Note também que o polinômio de Taylor do seno é uma função ímpar.
Qual o polinômio de Taylor, em torno de $x=0$ de $\ln(1+2x)$?
Vamos usar a aproximação de $\ln(1+x)$:
\[\ln(1+x) \approx x -\frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4}+ \frac{x^6}{6} + \cdots + \dfrac{(-1)^n x^{n+1}}{n+1}\]Substituindo $x$ por $2x$, escrevemos:
\[\ln(1+2x) \approx 2x -\frac{4x^2}{2} + \frac{8x^3}{3} - \frac{2^4x^4}{4}+ \frac{2^6x^6}{6} + \cdots + \dfrac{(-1)^n 2^{n+1}x^{n+1}}{n+1}\]O exemplo anterior induz uma pergunta natural. Suponha que $g(x)$ é uma função qualquer. Se $P(x)$ é polinômio de Taylor de $f$, será que $P(g(x))$ é o polinômio de Taylor de $f(g(x))$? Repare que foi exatamente isso que fizemos no exemplo anterior se pensarmos que $f(x) = ln(1+x)$ e $g(x) = 2x$. A resposta dessa pergunta depende de vários fatores. Vamos dar aqui uma resposta simples, que está longe de esgotar o assunto, mas ajuda em vários problemas.
Suponha que $f \in C^{\infty}(I_{0})$ em que $I_{0}$ é algum intervalo em torno de $0$. Suponha que o polinômio de Taylor de ordem $n$ de $f(x)$ em torno de $0$ é $P(x)$. Então, $P(ax^j)$ é polinômio de Taylor (de alguma ordem) de $f(ax^j)$, em torno de $0$.
Obtenha o polinômio de Taylor, em torno de $0$ de ordem $10$ de $e^{x^2}$.
Sabemos que o polinômio de Taylor de $e^x$ é:
\[P(x) = 1 +x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \dfrac{x^n}{n!}\]Fazendo $P(x^2)$ podemos escrever:
\[e^{x^2} \approx 1 + x^2 + \frac{x^4}{2!} + \frac{x^6}{3!} + \frac{x^8}{4!}+ \frac{x^{10}}{5!}\]Obtenha o polinômio de Taylor de $\mathrm{sen}(x^3)$ em torno de $x=0$.
Sabemos que o polinômio de Taylor de $\mathrm{sen}(x)$ é dado por:
\[x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + \dfrac{(-1)^n x^{2n+1}}{(2n+1)!}\]Substituindo $x$ por $x^3$, temos o polinômio de $\mathrm{sen}(x^3)$:
\[x^3 - \frac{x^9}{3!} + \frac{x^{15}}{5!} - \frac{x^{21}}{7!} + \cdots + \dfrac{(-1)^n x^{6n+3}}{(2n+1)!}\]Lema: Se $p(x)$ é um polinômio de grau $n$ o polinômio de Taylor de ordem $n$ de $p(x)$ é ele mesmo.
Para concluir essa discussão, por ora, fazemos algumas observações sobre polinômios de Taylor em geral.Polinômios de Taylor são usados para aproximar funções perto de algum ponto de seu domínio.
Para que um polinômio de grau $n$ possa ser calculado em torno de um ponto, é suficiente que a função tenha $n+1$ derivadas no ponto.
O erro na aproximação em tornos de $x_0$ por um polinômio de grau $n$ em um ponto $x $ tende a $0$ mais rápido que $(x-x_0)^n$, supondo que a função tenha $n+1$ derivadas contínuas.

