Imagem e Gráfico
O Conjunto Imagem de uma função $f$ é denotado por $Im(f)$ e é definido como
$Im(f)=\left\{f(x)\in B;x\in \mathrm{D}(f) \right\}$.
Assim, $Im(f)$ é um subconjunto do contradomínio $B$, $Im(f)\subset B$. Pode ocorrer de $Im(f)= B$ ou não, nesse caso serão conjuntos distintos, isto é $Im(f)\varsubsetneq B$.
A função definida por $f(x)=x+4$, $x\in \mathbb{R}$, tem como conjunto imagem todos os reais. De fato, dado qualquer número real $y$, ele pode ser escrito como imagem do número real $y-4$, ou seja, pela lei de formação da $f$, a imagem de $y-4$ é dada por $f(y-4)=(y-4)+4=y$.
A função definida por $f(x)=x^2+1$, $x\in \mathbb{R}$, tem como conjunto imagem o intervalo $[1,+\infty)$. De fato, pense na parábola que está associada à expressão da função, qualquer número $y\geq1$ no eixo $y$ está associado a um valor de $x$ real, tal que $y=x^2+1$.
O Gráfico de uma $f$ é denotado por $Gr(f)$ e é definido como
$Gr(f)=\left\{(x,f(x))\in \mathbb{R}^2;x\in \mathrm{D}(f) \right\}$.
Note que o $Gr(f)$ é um subconjunto do plano $\mathbb{R}^2$, formado pelos pares ordenados onde a primeira coordenada é um ponto do domínio e a segunda coordenada é a imagem correspondente.
O comportamento de uma função é claramente visualizado através de seu gráfico, que é o conjunto dos pares ordenados $Gr(f)=\left\{(x,f(x))\in \mathbb{R}^2;x\in \mathrm{D}(f)\right\}$. O esboço do gráfico no plano cartesiano nos fornece o comportamento da $f$, seu domínio e sua imagem. De fato, repare que, dado o gráfico da função, como ele só contém pontos da forma $(x,f(x)), x \in \mathrm{D}(f)$, podemos descobrir o domínio da função projetando o gráfico sobre o eixo $x$. Da mesma forma, se projetarmos o gráfico sobre o eixo y, teremos a imagem da função, pois só pontos com ordenada $y=f(x)$ estarão no gráfico.
Quando o $\mathrm{D}(f)$ é um intervalo ilimitado, procuramos traçar uma parte do seu gráfico que contenha todas as suas propriedades interessantes, como raízes, pontos de mudança de crescimento, onde ocorrem saltos, entre outros, e tal que se tenha uma ideia do que ocorre no restante do gráfico.
Observação: Uma forma de saber se uma curva no plano $xy$ pode ou não ser o gráfico de uma função de $x$, é fazendo o teste da reta vertical. Se alguma reta vertical intersectar a curva em mais de um ponto, esta curva não pode ser o gráfico de uma função de $x$, pois estaríamos associando a um determinado ponto $x$ do domínio, mais do que apenas um ponto do contradomínio. Por outro lado, se toda reta vertical intersectar a curva em no máximo um ponto, então essa curva é gráfico de uma função de $x$.
As duas curvas a seguir não são gráficos de uma função de $x$.
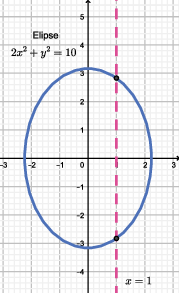
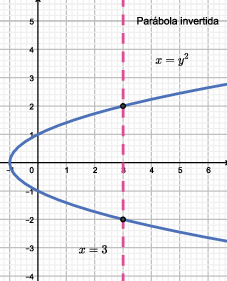
Na próxima seção veremos exemplos de gráficos básicos de funções, com os quais trabalharemos no restante do curso.
Tipos Básicos de Gráficos de Funções
Já sabemos que $f(x)=bx+c$, $x\in \mathbb{R}$, onde $b$ e $c$ são constantes, é dita uma função afim. O gráfico é uma reta horizontal, se $b=0,$ ou uma reta inclinada, se $b\neq 0$.
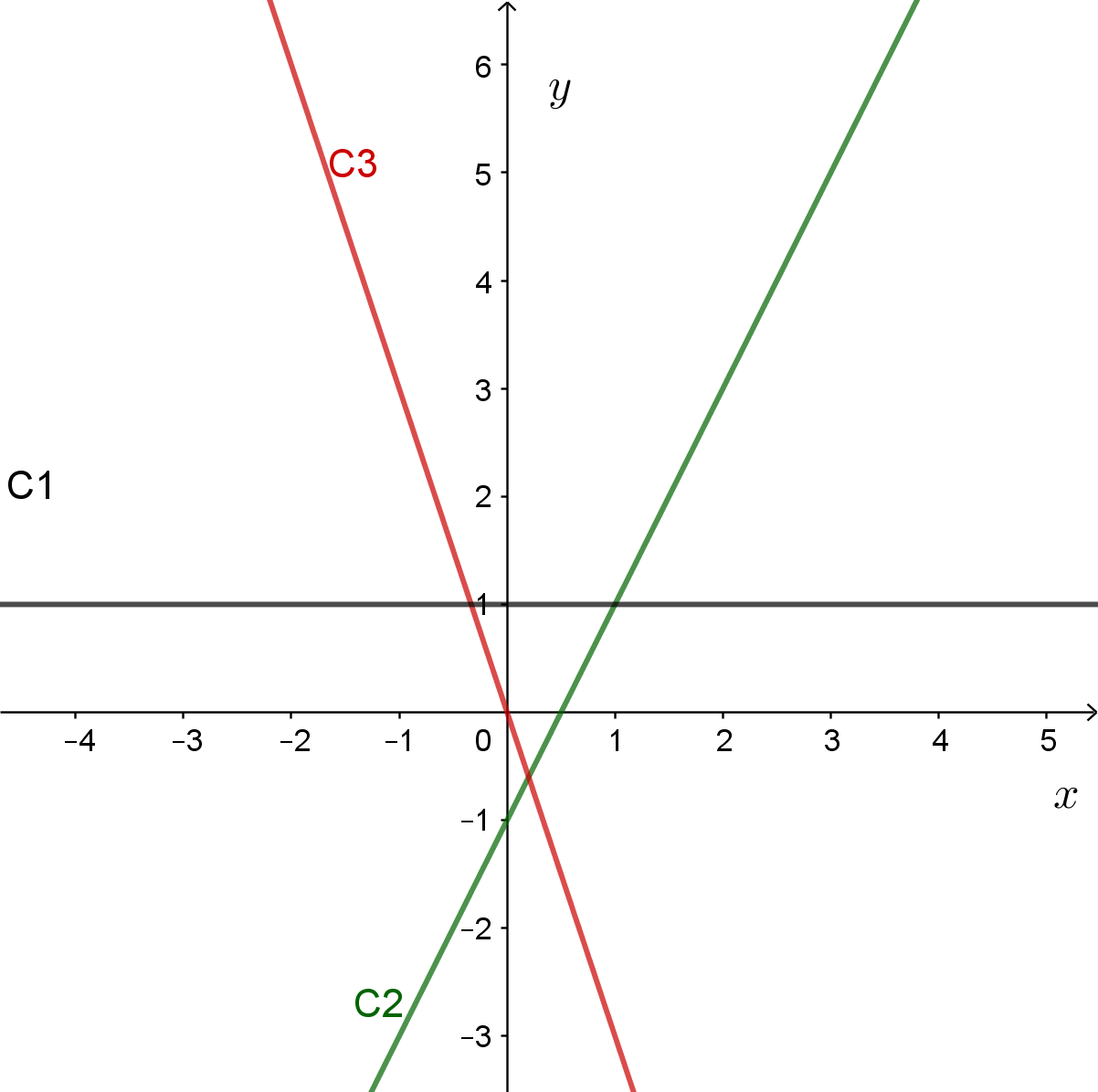
$c_1$ é a reta $y=1$, $c_2$ é $y=2x-1$ e $c_3$ é $y=-3x$.
Excetuando as retas horizontais $(b=0)$, o conjunto imagem de uma reta é todos os reais $\mathbb{R}$.
Considere a função definida por $f(x)=x^2$, $x\in \mathbb{R}$. O gráfico é uma parábola, que ao projetar no eixo $y$, permite obter o conjunto imagem $[0,+\infty)$.
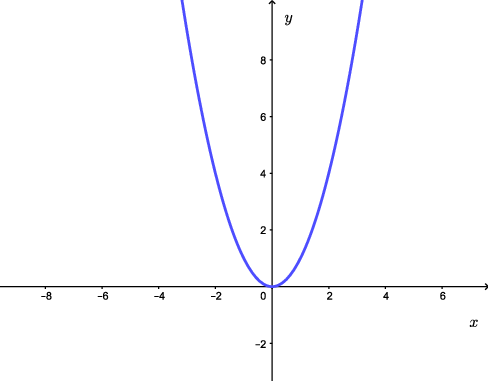
O conjunto imagem é $[0,+\infty)$.
Considere a função definida por $f(x)=\sqrt{x}$, $x\geq 0$. Note, pela observação do gráfico abaixo, que projetando o gráfico no eixo $y$, temos $Im(f)=[0,+\infty)$.
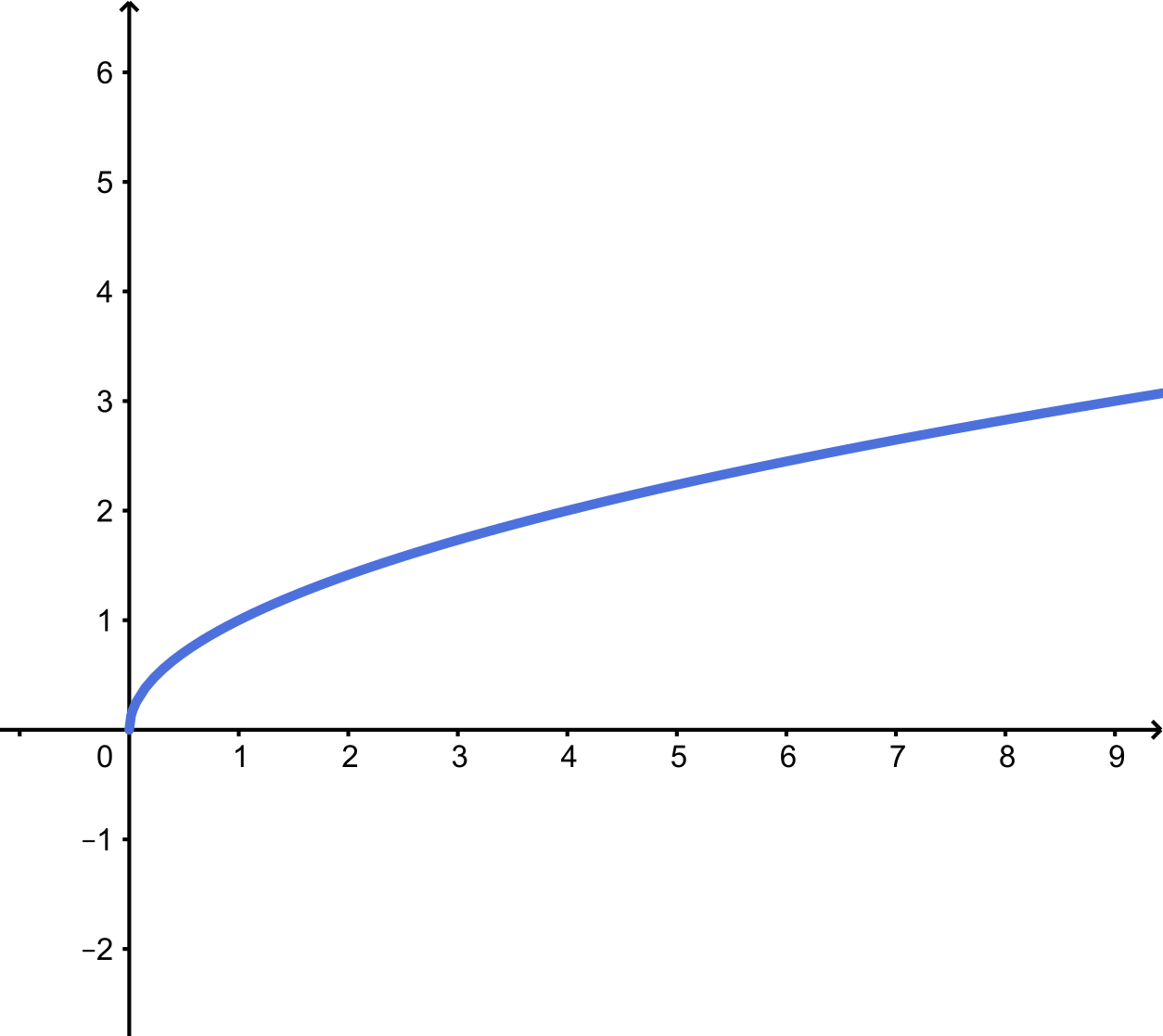
O conjunto imagem é $[0,+\infty)$.
Considere a função definida por $f(x)=\dfrac{1}{x}$, $x\neq 0$. O gráfico é uma hipérbole. Observe o comportamento do gráfico, para $x>0$ aumentando, $1/x$ diminui e se aproxima do zero (nunca será igual a zero!). Analogamente, se $x<0$ diminui, então $1/x$ se aproxima de zero por valores negativos. Por outro lado, se $x>0$ fica muito pequeno, isto é, próximo de zero, então $1/x$ aumenta de forma ilimitada (dizemos que tende a infinito). Se $x<0$ se aproxima de zero, então $1/x$ é negativo e se torna ilimitado (dizemos que tende a menos infinito). O gráfico de qualquer potência ímpar negativa de $x$, a saber $y=x^{-3}=\dfrac{1}{x^3}$, $y=x^{-5}=\dfrac{1}{x^5}$, $y=x^{-7}=\dfrac{1}{x^7}$, tem o mesmo aspecto do gráfico abaixo.
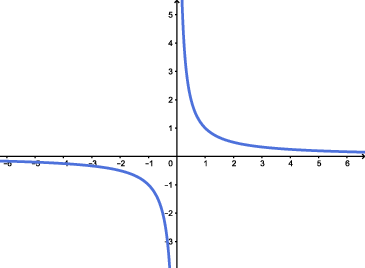
O conjunto imagem é $(-\infty,0)\cup(0,+\infty)$.
Considere a função definida por $f(x)=\dfrac{1}{x^2}$, $x\neq 0$. O gráfico de qualquer potência par negativa de $x$, a saber, $y=x^{-4}=\dfrac{1}{x^4}$, $y=x^{-6}=\dfrac{1}{x^6}$, $y=x^{-8}=\dfrac{1}{x^8}$, tem o mesmo aspecto do gráfico abaixo.
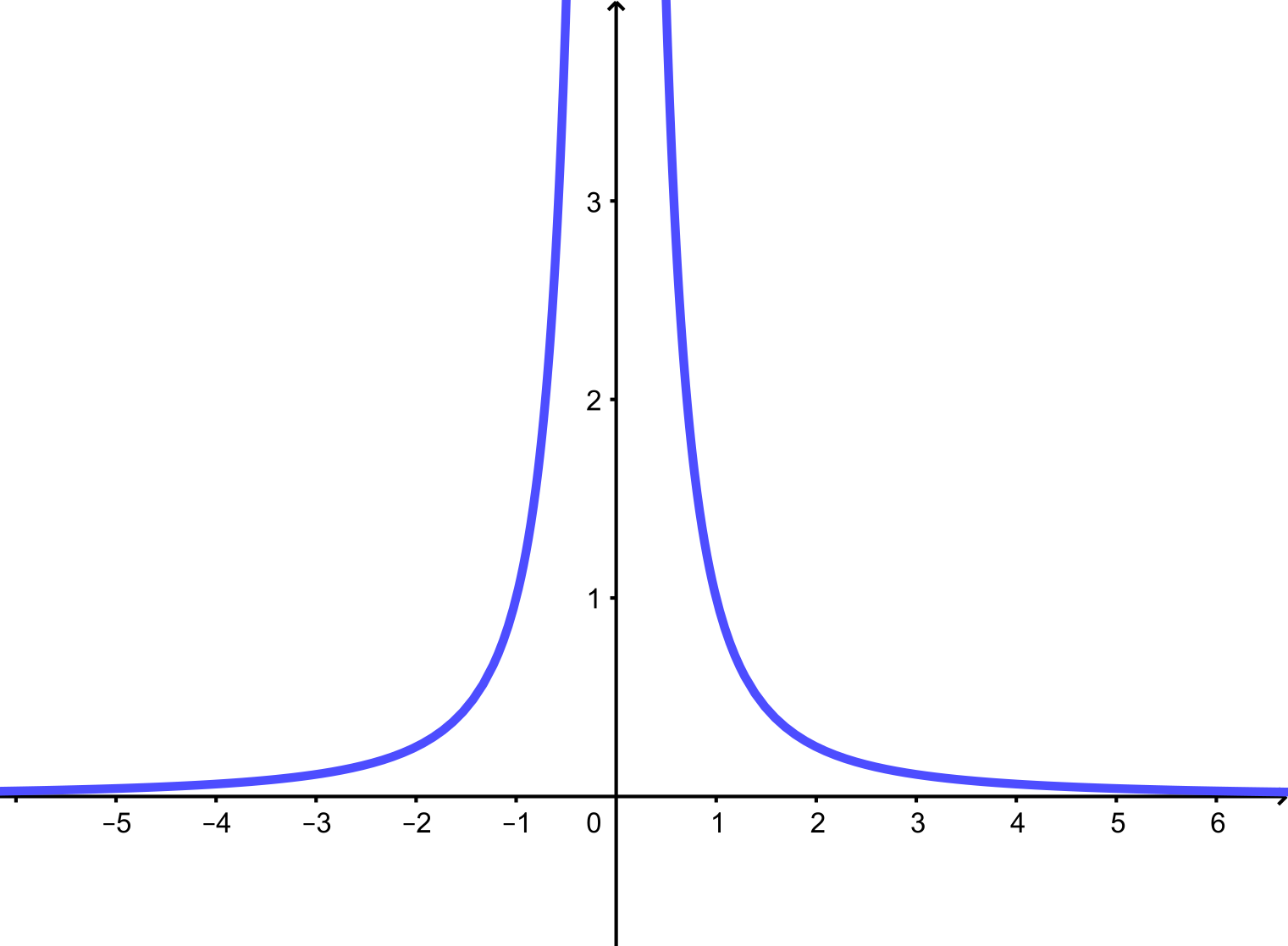
O conjunto imagem é $(0,+\infty)$.
Considere a função definida por $f(x)=x^3$, $x\in \mathbb{R}$. O gráfico de qualquer potência inteira $n\geq 3$ ímpar de $x$, a saber $y=x^{5} $, $y=x^{7} $, $y=x^{9} $, tem o mesmo aspecto do gráfico abaixo.
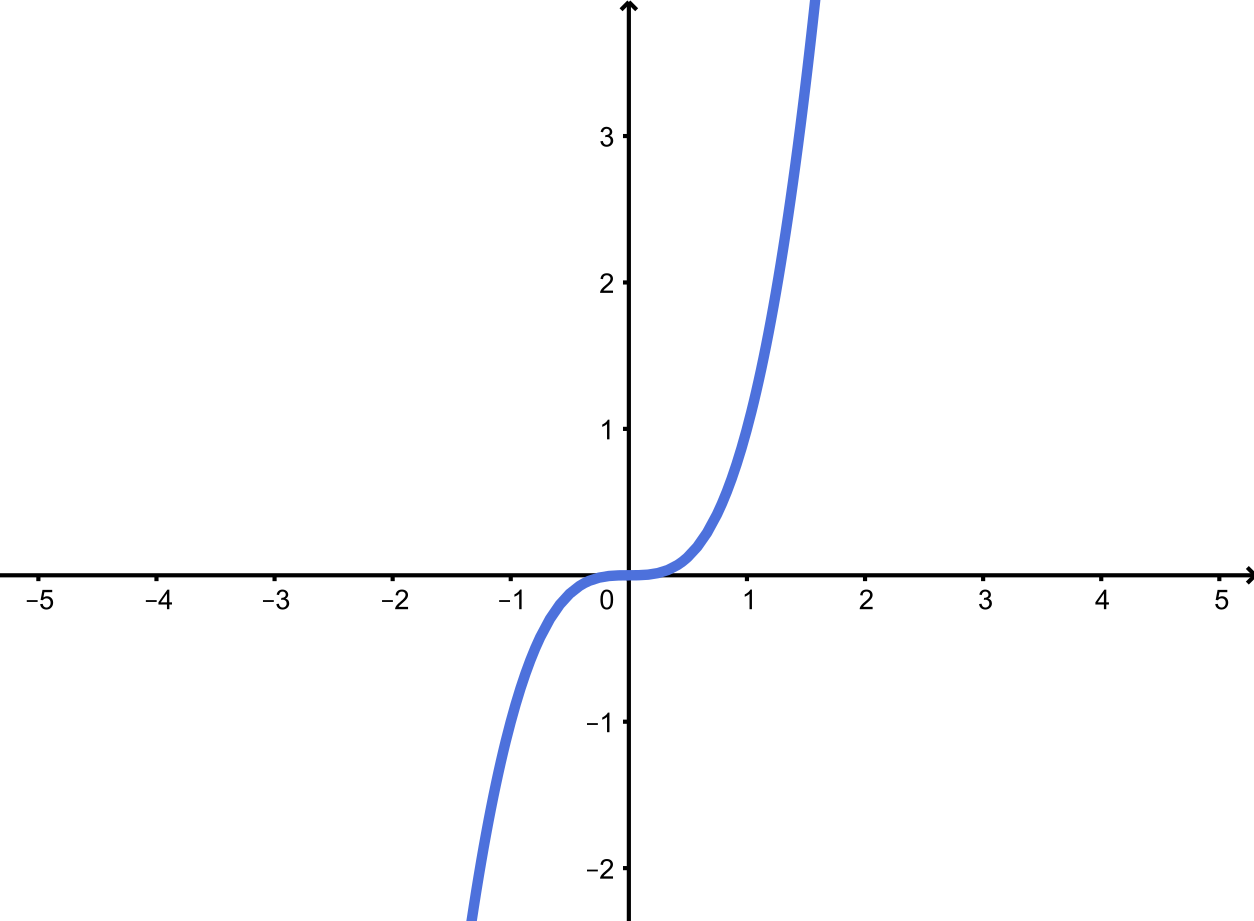
O conjunto imagem é $\mathbb{R}$.
Considere a função definida por $f(x)=x^4$, $x\in \mathbb{R}$. O gráfico de qualquer potência $n\geq 2$ par de $x$, a saber $y=x^{6} $, $y=x^{8} $, $y=x^{10} $, tem o mesmo aspecto do gráfico abaixo.
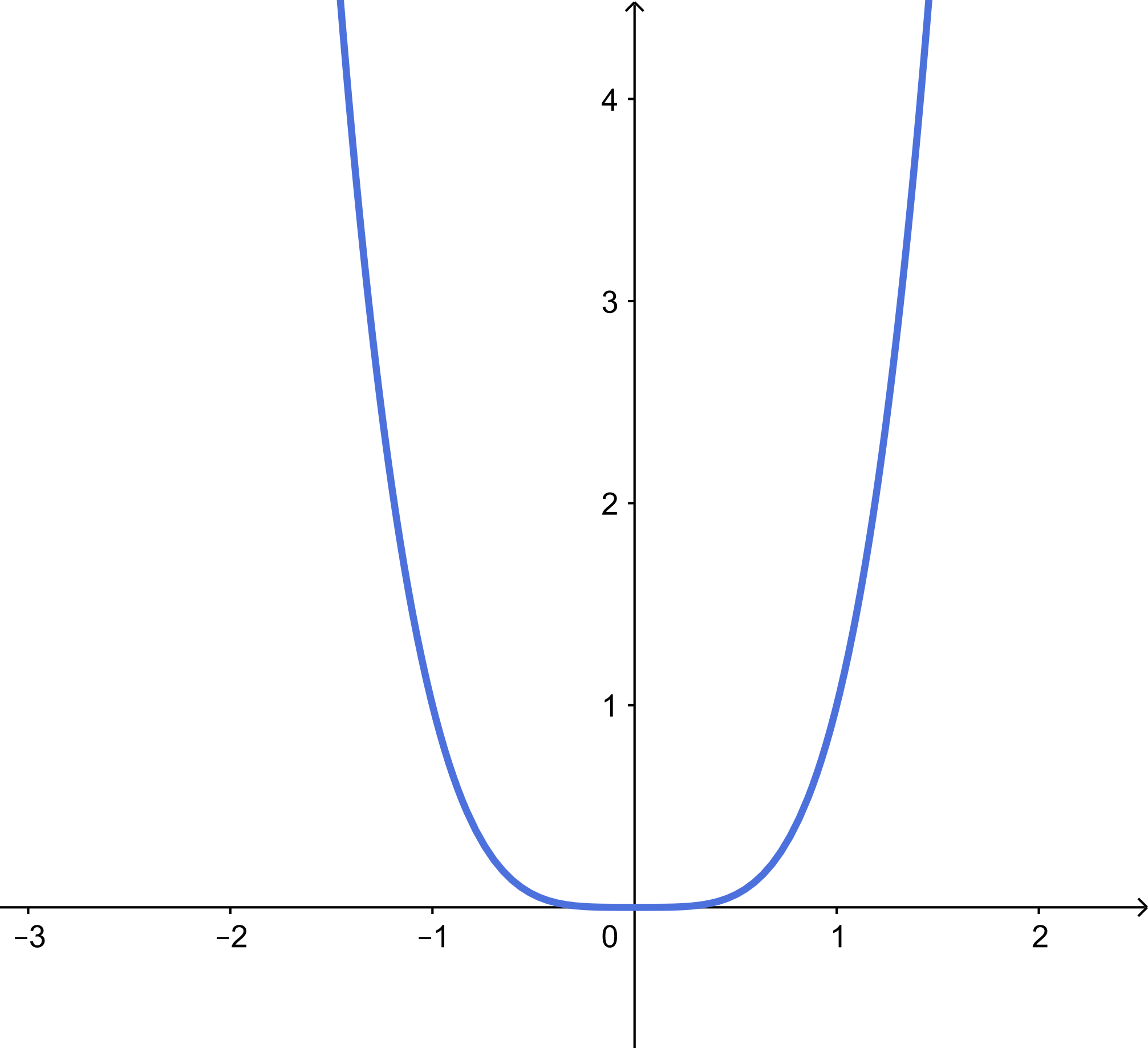
O conjunto imagem é $[0,+\infty)$.
Observação: Vamos relembrar as definições de raízes de índice ímpar e par. Dado $n \in \mathbb{N}$
- A raiz de índice (ímpar) $2n+1$ de um número real $a\in\mathbb{R}$ é definida como o número real denotado por $\sqrt[2n+1]{a}$, tal que $(\sqrt[2n+1]{a})^{2n+1}=a$ e raiz $2n+1$ de 0 é 0. No caso de raiz de índice ímpar, a raiz tem o mesmo sinal do radicando $a$.
- A raiz de índice (par) $2n$ de um número real $a>0$ é definida como o número real positivo denotado por $\sqrt[2n]{a}$, tal que $(\sqrt[2n ]{a})^{2n}=a$ e raiz $2n$ de 0 é 0.
$y=\sqrt[3]{x}$, $x\in \mathbb{R}$. O gráfico de qualquer raiz de índice ímpar de $x$, a saber, $y=\sqrt[5]{x}, y=\sqrt[7]{x}$, tem o mesmo aspecto do gráfico abaixo.
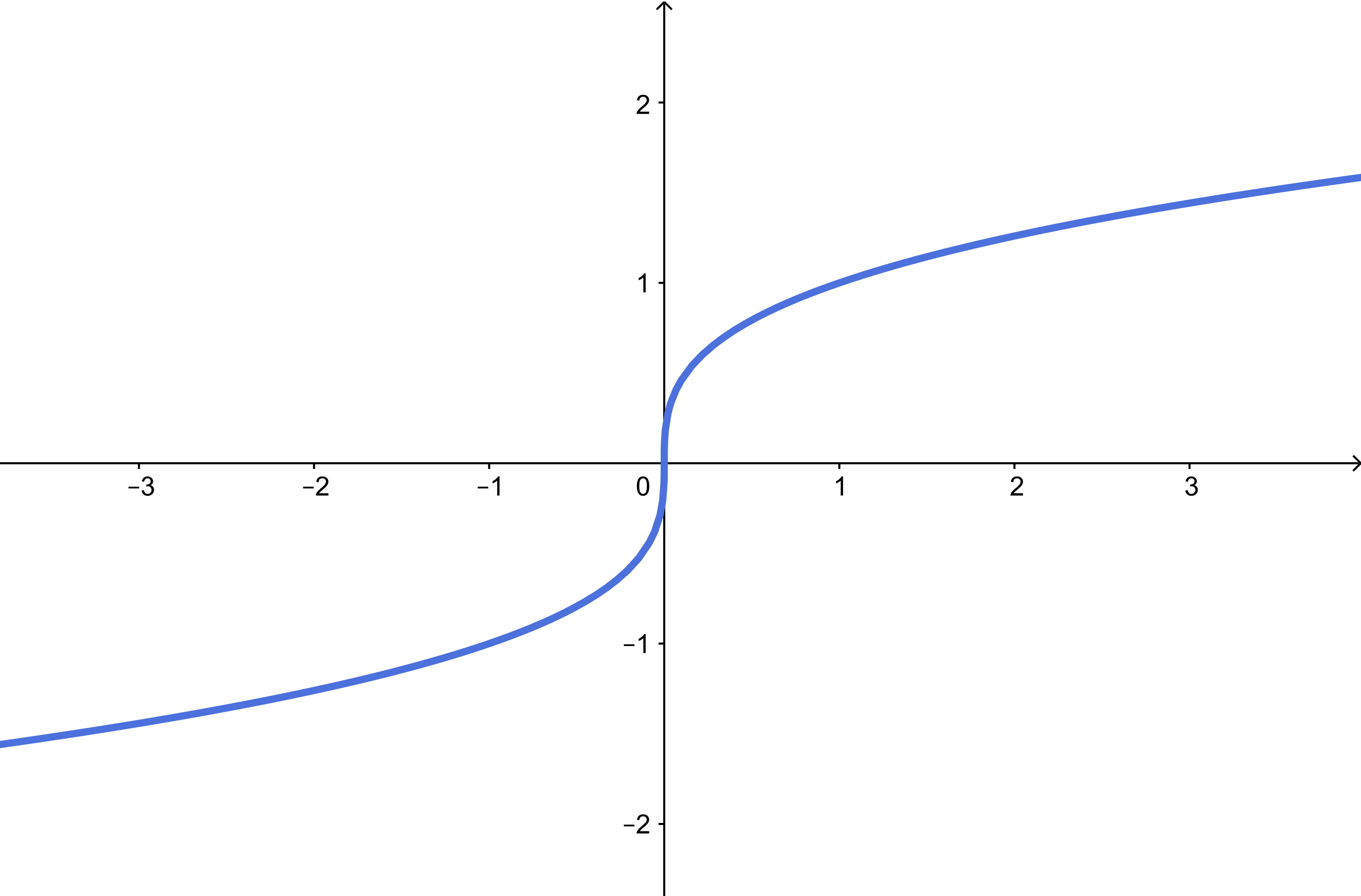
O conjunto imagem é $\mathbb{R}$.
$y=\sqrt[4]{x}$, $x\geq 0$. O gráfico de qualquer raiz de índice par de $x$, a saber, $y=\sqrt[6]{x}, y=\sqrt[8]{x}$, tem o mesmo aspecto do gráfico abaixo.
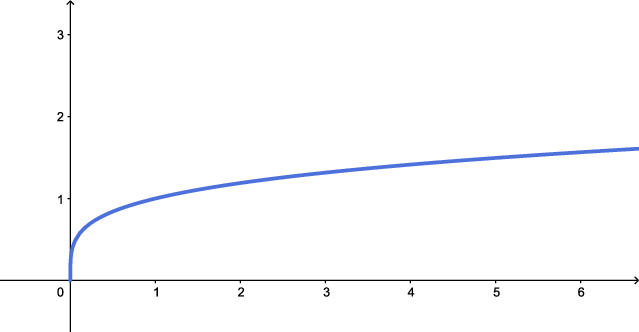
O conjunto imagem é $[0,+\infty)$.

