Introdução - Derivação das Funções Exponenciais e Logarítmicas
Nesta semana, estudaremos a derivação da função exponencial e logarítmica, e depois os Teoremas de Rolle e do Valor Médio, e uma importante consequência deste último, a Regra de L´Hospital.
Função Exponencial
Imagine uma grandeza cuja variação se mantenha sempre em uma mesma razão a cada intervalo de tempo fixado. Por exemplo, uma população de bactérias que aumente em 50% o número de indivíduos a cada hora, ou uma amostra de material cuja massa de isótopos radioativos diminua 10% a cada ano, decaindo em isótopos não radioativos.
Funções exponenciais serão da forma
\[\begin{array}{rccl}f:&\mathbb{R}&\rightarrow&\mathbb{R}\\&x&\mapsto&y=f(x)=a^x\end{array}\]onde \(a\) é um número real com \(a>0\).
Entre as funções exponenciais, se destaca a de base $e=2.71828182846\dots$. Sendo $f(x)=e^x$, sua derivada é a própria $f$, isto é $f'(x) = \left(e^x\right)' = e^x = f(x)$.
Teorema do Valor Médio
Nas próximas semanas veremos como podemos estudar o comportamento das funções através do conhecimento de propriedades das suas derivadas de primeira e de segunda ordem. O que nos permite esse estudo é o Teorema de Valor Médio, que nos ajuda a entender, por exemplo, que se uma função tem derivada identicamente nula em um intervalo, então ela é constante no referido intervalo. Além disso, veremos que se o sinal da derivada de 1ª ordem for preservado em um intervalo, então a função será monótona, ou seja para sinal positivo, será estritamente crescente e se o sinal for negativo, estritamente decrescente. Outra ferramenta importante será a Regra de L'Hospital, que nos permite calcular limites, a princípio indeterminados, considerando as derivadas das funções envolvidas.
Abaixo temos $A=(a,f(a))$ um ponto sobre o gráfico da função $f$ e $A'=(a,f'(a))$ o ponto correspondente sobre o gráfico da função derivada $f'$ de mesma abscissa. Mova o ponto $A$ ou a abscissa $a$ e acompanhe como a mudança no sinal da imagem $f'(a)$ interfere no crescimento da função $f$.
//
Derivada da Função Exponencial e da Função Logarítmica
Nesta seção, veremos uma das funções mais presentes na modelagem de fenômenos naturais, a função exponencial. Esta função está por trás de qualquer fenômeno em que a taxa de variação de uma grandeza é proporcional ao valor da própria grandeza. É fácil listar fenômenos deste tipo: crescimento populacional, juros e decaimento radioativo. Como você já viu nas semanas 5 e 6, a derivada de uma função em um ponto $x$ representa uma taxa de variação instantânea da função, ou uma tendência de crescimento/decrescimento. Assim, como veremos logo abaixo, a derivada de uma função exponencial será sempre proporcional ao valor da função. A partir daí, intuiremos a existência de uma base especial, um número que denotaremos por $e$, que torna a expressão da derivada ainda mais interessante. Depois, estudaremos a função inversa à exponencial nesta base $e$, a função logarítmica em base natural, que chamaremos de $\ln$.
Parte do conteúdo apresentado aqui é feito também no vídeo que você deve assistir:
Caso você acredite que precisa rever alguns conceitos mais elementares de funções exponenciais, recomendamos assistir aos vídeos de revisão:
A Função Exponencial
Observação: Se você já possui bastante familiaridade com a função exponencial, ou está querendo chegar logo aos resultados sobre derivação desta função, pode pular direto para a seção A Derivada da Função Exponencial.
Vamos denotar uma grandeza que varia em função do tempo por $y(t)$. A variação da grandeza $y(t)$ depende, obviamente, do fenômeno estudado. Porém, em muitos fenômenos naturais, observa-se que, a razão de crescimento $y(t)$ é a mesma sempre que se passa um mesmo intervalo de tempo.
Imagine uma população de bactérias, inicialmente com 1.000.000 de indivíduos, que dobre a cada 1 hora, enquanto não houver restrição que dificulte este crescimento.
Vamos considerar o tempo do início da observação como $t=0$. Teremos um crescimento como abaixo:
| $t$ | 0 | 1 | 2 | 3 | 4 | 5 |
| População $y(t)$ | 1.000.000 | 2.000.000 | 4.000.000 | 8.000.000 | 16.000.000 | 32.000.000 |
A cada hora, a população será o dobro da anterior. A partir disso, podemos obter uma expressão para a população $y(t)$, quando $t$ for um inteiro não-negativo.
| $y(0)$ | $=$ | $1.000.000$ | $=$ | $1.000.000 \cdot 1$ | = | $1.000.000$ | $\cdot$ | $2^0$ | |
| $y(1)$ | $=$ | $2.000.000$ | $=$ | $\left(1.000.000 \cdot 2^0\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^1$ | |
| $y(2)$ | $=$ | $4.000.000$ | $=$ | $\left(1.000.000 \cdot 2^1\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^2$ | |
| $y(3)$ | $=$ | $8.000.000$ | $=$ | $\left(1.000.000 \cdot 2^2\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^3$ | |
| $\vdots$ | |||||||||
| $y(t)$ | $=$ | $(1.000.000\cdot 2^{t-1}) \cdot 2$ | $=$ | $1.000.000$ | $\cdot$ | $2^t,$ | para $t \in \mathbb{N}$ |
Também é razoável imaginar que, 1 hora antes do estudo, ou seja, quando $t=-1$, a população de bactérias era a metade da população em $t=0$, isto é,
\[y(-1) = y(0) \cdot \frac{1}{2} = 1.000.000\cdot 2^{-1}.\]Duas horas antes do início, a população seria 1/4 de $y(0)$, três horas antes ($t=-3$), seria 1/8 de $y(0)$, e assim por diante, para que, depois de dobrar 2 ou 3 vezes, respectivamente, a população se tornasse $y(0)$.
Assim, teríamos
| $y(-2)$ | $=$ | $1.000.000 \cdot \frac{1}{4}$ | = | $1.000.000$ | $\cdot$ | $2^{-2}$ |
| $y(-3)$ | $=$ | $1.000.000 \cdot \frac{1}{8}$ | = | $1.000.000$ | $\cdot$ | $2^{-3}$ |
| $\vdots$ |
Com isso, $y(t) = 1.000.000\cdot 2^{t}$ para todo $t \in \mathbb{Z}$, ou seja, $t$ inteiro, positivo, 0 ou negativo.
E qual seria o crescimento a cada intervalo de meia hora? Estamos supondo que o crescimento relativo é o mesmo em intervalos iguais de tempo. Assim, o fator de crescimento de $y(0)$ para $y(0,5)$ será o mesmo de $y(0,5)$ para $y(1)$, ou seja,
\[y(0,5) = a\cdot y(0)\] \[y(1) = a\cdot y(0,5)\]Substituindo o $y(0,5)$ da primeira linha na segunda, temos que
\[y(1) = a\cdot (a\cdot y(0)) = a^2\cdot y(0).\]Mas sabemos que $y(1) = 2\cdot y(0)$, logo
\[2y(0) = a^2\cdot y(0) \therefore a^2 = 2 \therefore a = \sqrt{2} = 2^{0,5}\](obviamente desprezamos a possibilidade $a=-\sqrt{2}$, pois não faz sentido real no problema).
De maneira geral, a cada intervalo de $1/n$ hora, teremos um mesmo crescimento relativo, logo
\begin{eqnarray*}y\left(\frac{1}{n}\right) = b \cdot y(0)\\y\left(\frac{2}{n}\right) = b \cdot y\left(\frac{1}{n}\right) &\therefore& y\left(\frac{2}{n}\right) = b^2 y(0)\\y\left(\frac{3}{n}\right) = b \cdot y\left(\frac{2}{n}\right) &\therefore& y\left(\frac{2}{n}\right) = b^3 y(0)\\\vdots \\y\left(\frac{n-1}{n}\right) = b \cdot y\left(\frac{n-2}{n}\right) &\therefore& y\left(\frac{n-1}{n}\right) = b^{n-1} y(0)\\y(1) = b\cdot y\left(\frac{n-1}{n}\right)&\therefore& y(1) = b^n\cdot y(0)\end{eqnarray*}mas como $y(1) = 2y(0)$, temos $b^n\cdot y(0) = 2y(0)$, logo $b = \sqrt[n]{2}$. Com isso, a população de bactérias aumenta $\sqrt[n]{2}$ a cada $1/n$ hora. Portanto, passados $m$ períodos de $1/n$ horas, a população terá aumentado $\left(\sqrt[n]{2}\right)^m = 2^{m/n}$ vezes e, com isso,
\[y(m/n) = 1.000.000 \cdot 2^{m/n}.\]Até aqui, já concluímos que $y(t) = 1.000.000\cdot 2^t$ para todo $t \in \mathbb{Q}$, isto é, para todo $t$ que possa ser escrito como uma fração $m/n$, com $m$ e $n$ inteiros, $n\neq 0$.
E se $t$ for um número irracional? Qual seria a população de bactérias? É natural acreditarmos que continuaria sendo dada por $y(t) = 1.000.000 \cdot 2^t$, porém, o que seria $2^t$ neste caso? Tentaremos responder a esta pergunta somente depois.
Imagine que, no exemplo anterior, a população inicial de bactérias é $y(0) = C$, e a cada hora decorrida, a população é multiplicada por $a > 1$. Neste caso, teríamos
| $y(0)$ | $=$ | $C$ | $=$ | $C \cdot 1$ | = | $C$ | $\cdot$ | $a^0$ | |
| $y(1)$ | $=$ | $C\cdot a$ | $=$ | $\left(C \cdot a^0\right)\cdot a$ | = | $C$ | $\cdot$ | $a^1$ | |
| $y(2)$ | $=$ | $C\cdot a^2$ | $=$ | $\left(C \cdot a^1\right)\cdot a$ | = | $C$ | $\cdot$ | $a^2$ | |
| $y(3)$ | $=$ | $C\cdot a^3$ | $=$ | $\left(C \cdot a^2\right)\cdot a$ | = | $C$ | $\cdot$ | $a^3$ | |
| $\vdots$ | |||||||||
| $y(t)$ | $=$ | $(C\cdot a^{t-1}) \cdot a$ | $=$ | $C$ | $\cdot$ | $a^t,$ | para $t \in \mathbb{N}$ |
Como no exemplo anterior, poderíamos estender a expressão para qualquer $t \in \mathbb{Q}$, isto é, qualquer $t=m/n$, com $m$ e $n$ inteiros, $n \neq 0$. Teríamos que
\[y(t) = C\cdot a^t.\]Lembramos que $a^{m/n} = \left(\sqrt[n]{a}\right)^m = \sqrt[n]{a^m}$.
Os fenômenos descritos nos exemplos 1 e 2 são crescimentos exponenciais, de bases $2$ e $a$, respectivamente. Note que temos crescimento pois $2> 1$ e $a > 1$.
Imagine que, a massa de isótopos radioativos em uma certa amostra de material reduza em 20% a cada ano. Assim, a cada passagem de um ano, a massa de isótopos radioativos será 20% menor que no ano anterior, isto é,
\[y(t+1) = y(t) - 20\%\,y(t) = \frac{100\,y(t)}{100} - \frac{20\,y(t)}{100} = \frac{80y(t)}{100} = \frac{4}{5}y(t).\]Com isso, vemos que, a cada intervalo de um ano, a massa radioativa é multiplicada por $\frac{4}{5}$. Sendo $C$ a massa inicial, isto é, $y(0) = C$, teremos então
\[y(t) = C \cdot \left(\frac{4}{5}\right)^t\]O fenômeno do exemplo 3 é um decaimento exponencial, de base $4/5$. Note que temos um decaimento pois a base é menor do que 1.
Uma função $f:\mathbb{R}\rightarrow\mathbb{R}$ será exponencial se sua expressão for da forma
\[f(x)=a^x,\]para algum número real $a > 0$.
Já vimos que, se $t=m/n \in \mathbb{Q}$, temos
\[f(a) = a^t = a^{m/n} = \left(\sqrt[n]{a}\right)^m.\]Porém, ainda precisamos definir claramente o que representa $f(t) = a^t$ quando $t$ é irracional, isto é, não pode ser escrito na forma $m/n$, com $m$ e $n$ inteiros, $n \neq 0$.
Lembre-se, porém, que um número irracional $t$ pode ser escrito na forma decimal (infinita) como
\[t = K\!,a_1a_2a_3a_4... \]onde $K$ é a parte inteira e $a_1$, $a_2$, ... são os dígitos da parte decimal, isto é, cada $a_i$ é um algarismo de 0 a 9. Desta forma, podemos aproximar $t_0$ por
\[t_1 = K\!,a_1 \] \[t_2 = K\!,a_1a_2 \] \[t_3 = K\!,a_1a_2a_3 \] \[t_4 = K\!,a_1a_2a_3a_4 \] \[\vdots\]e a aproximação será tão boa quanto quisermos, bastando acrescentar mais dígitos. Assim, podemos dizer que $t_n \to t$ quando $n \to +\infty$.
É razoável supormos que a função exponencial seja contínua, uma vez que a estamos utilizando para modelar fenômenos naturais. Assim, como estamos supondo $f(x) = a^x$ contínua e como temos $t_i \to t$, temos
\[f(t) = \lim_{s\to t}f(s).\]Como $t_i \to t$, isto é, os $t_i$'s se aproximam de $t$, logo os valores $f(t_1)$, $f(t_2)$, ... se aproximam de $f(t)$.
Em outras palavras, à medida em que aproximamos o número irracional $t$ por $t_1$, $t_2$, $t_3$, ..., estaremos obtendo aproximações $f(t_1)$, $f(t_2)$, $f(t_3)$, ..., cada vez melhores de $f(t)$.
Na expressão da função exponencial, $f(x)=a^x$, a base, $a$, é um número real positivo fixo, o que varia é o expoente $x$. É diferente, portanto, de uma função potência, com expressão na forma $g(x) = x^n$, em que o expoente é fixo e a base é quem varia.
O gráfico da função exponencial é como um dos gráficos abaixo, dependendo do valor de $a$.
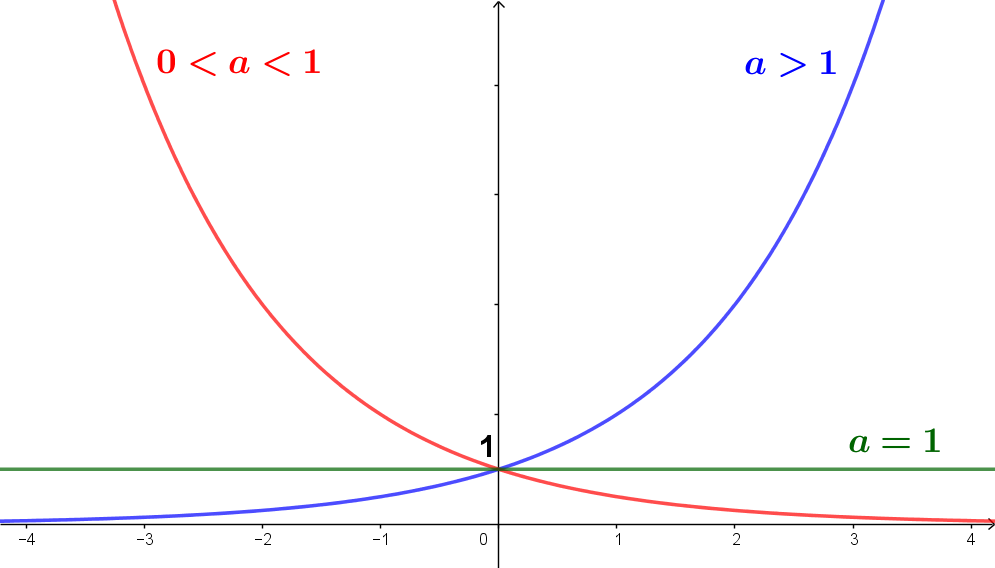
Observe que, quando $a=1$ a função é constante e igual a 1, pois $1^x= 1$ para todo $x \in \mathbb{R}$. Para toda base $a>0$, teremos $f(0)=1$.
Outra observação importante é que a função exponencial $f(x)=a^x$, $a>0$, é sempre positiva, isto é, $f(x) > 0$ para todo $x \in \mathbb{R}$.
E qual é a relação da função exponencial com a derivação?
Voltando à discussão do começo desta seção, se chamarmos de $y(t)$ uma grandeza que varia em função do tempo $t$, muitos fenômenos naturais (não todos, mas muitos) obedecem à Lei do Crescimento ou Decaimento Natural, na qual
\[\frac{dy}{dt} = k\cdot y,\]ou, escrita com outra notação
\[y'(t) = k\cdot y.\]Veremos na próxima seção que as funções exponenciais são soluções para esta equação.
Em fenômenos que obedecem à Lei do Crescimento ou Decaimento Natural, a tendência de variação da grandeza é proporcional ao tamanho da grandeza. É bem plausível acreditarmos que um crescimento populacional (que já vimos ser modelado por uma função exponencial multiplicada por uma constante) obedeça a uma lei como esta, pelo menos enquanto não houver qualquer limitação de recursos para a população. Quanto mais indivíduos houver, tanto maior será o crescimento populacional esperado.
A Derivada da Função Exponencial
Já vimos que uma função $f:\mathbb{R}\rightarrow\mathbb{R}$ será exponencial se sua expressão for da forma
\[f(x)=a^x,\] para algum número real $a > 0$.
Esta função é contínua em todo o domínio $\mathbb{R}$. Veremos agora que é diferenciável e calcularemos a derivada. Sabemos que a derivada de uma função em $x$ é definida por um limite que pode ser escrito como:
\[f'(x) =\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}.\]Se tentarmos calcular a derivada da função exponencial a partir do limite acima, teremos:
\begin{eqnarray}\nonumber f'(x) &=& \lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}\\ \\\nonumber &=& \lim_{h\to 0}\dfrac{a^{x+h}-a^{x}}{h}\\ \\\tag{1} &=& \lim_{h\to 0}\dfrac{a^x\left(a^h-1\right)}{h}\\ \\\tag{2} &=& a^x\cdot\lim_{h\to 0}\dfrac{a^h-1}{h}.\end{eqnarray}
Por outro lado, a derivada em $x=0$, será dada por
\begin{eqnarray*}f'(0) &=& \lim_{h\to 0}\dfrac{f(0+h)-f(0)}{h}\\&=& \lim_{h\to 0}\dfrac{a^{h}-a^0}{h}\\&=& \lim_{h\to 0}\dfrac{a^h-1}{h}.\end{eqnarray*}Comparando esta expressão de $f'(0)$ com a obtida em 2, vemos que
\[f'(x) = a^x\cdot\lim_{h\to 0}\dfrac{a^h-1}{h} = a^x\cdot f'(0),\]ou seja, a derivada da função exponencial $f(x)=a^x$ é, para todo valor de $x\in \mathbb{R}$, igual à própria função $f(x)=a^x$, multiplicada pela constante $f'(0)$. Com isso, mostramos o que foi afirmado na introdução desta seção, que a derivada da exponencial é proporcional ao valor da função.
Isto nos leva a uma pergunta: será que existe algum valor para a base $a$ tal que $f'(0)$ seja igual a 1? A exponencial cresce tão mais rápido quanto maior é a base, o que reflete no valor da derivada em $x=0$. Observando os gráficos de $g(x)=2^x$ e $h(x)=3^x$ abaixo, percebemos que a reta $y=x+1$, de inclinação 1, fica entre estes dois gráficos em $x=0$.

Gráficos das funções $g(x)=2^x$ e $h(x)=3^x$.
Assim, é fácil acreditarmos que $g'(0)<1$ e $h'(0)>1$. Parece razoável, embora ainda careça de maior justificativa, acreditarmos que existe um número entre 2 e 3, que chamaremos de $e$ (chamado de número de Euler) tal que, se $f(x)=e^x$, temos $f'(0)=1$.
Com este número especial, definindo $f(x)=e^x$, teremos
\[\left(e^x\right)' = f'(x) = e^x \cdot f'(0) = e^x.\]Embora você possa estar pouco familiarizado com este $e$, acho que já podemos concordar que ele é um grande amigo do estudante de Cálculo. Exceto talvez pela derivada de uma constante (que é 0), a derivada da função exponencial de base $e$ é a mais amigável que você pode encontrar na disciplina.
\[\left(e^x\right)' = e^x.\]Voltaremos a falar um pouco mais sobre a misteriosa existência do número $e$ na seção ???, mas, por curiosidade, este número é dado por $e=2.71828182846...$. Note que é um número irracional, cuja expressão decimal é infinita e não segue qualquer padrão de repetição.
A exponencial de base $e$ é tão útil e especial que há uma notação específica para ela. É muito comum denotar a função $\exp:\mathbb{R}\to\mathbb{R}$, $\exp(x) = e^x$. Assim, $\exp'(x) = \exp(x)$.
Calcular $g'(x)$, sendo $g(x) = e^{f(x)}$, onde $f$ é diferenciável.
Aplicando a Regra da Cadeia, temos
\[g'(x) = \left[e^{f(x)}\right]' = e^{f(x)}\cdot \left[f(x)\right]' = e^{f(x)}\cdot f'(x) = f'(x)\,e^{f(x)}.\]Calcular $f'(x)$ se $f(x)=e^{\mathrm{sen}(x)}+\mathrm{sen}(e^x)$.
Derivando cada termo usando a regra da cadeia obtemos
$$y'=e^{\mathrm{sen}(x)}\cdot [\mathrm{sen}(x)]'+\cos(e^x)\cdot [e^x]'=e^{\mathrm{sen}(x)}\cos(x)+\cos(e^x)e^x.$$
Calcular $y'(x)$ onde $y=y(x)$ é implicitamente definida pela equação $x\cdot e^y=y\cdot \cos(x)$.
Nesse caso utilizamos derivação implícita e a regra do produto:
$$1\cdot e^y+x\cdot e^y\cdot y'=y'\cdot \cos(x)+y\cdot(-\mathrm{sen}(x)).$$Resolvendo para $y'$ obtemos
$$y'=\frac{e^y+\mathrm{sen}(x)y}{\cos(x)-xe^y}.$$
Relembrando a seção anterior, uma grandeza $y=f(x)$ obedecerá a Lei do Crescimento ou Decaimento Natural se
\[f'(x) = k\cdot f(x).\]Esta equação será satisfeita quando $f(x) = C\,e^{kx}$, com $C$ constante, pois
\[f'(x) = \left(C\,e^{kx}\right)' = C\,e^{kx}\cdot(kx)' = k\cdot C\,e^{kx} = k\cdot f(x).\]Assim, $f(x) = C\,e^{kx}$ é naturalmente uma expressão para fenômenos de crescimento ou decaimento exponencial. Em Cálculo 2A, você verá que $f(x) = C\,e^{kx}$ é, na realidade, a única forma de modelar tais fenômenos, isto é, a única solução para a equação diferencial $f'(x) = k\cdot f(x)$.
Vamos agora tentar encontrar uma expressão para a derivada da função exponencial com uma base diferente de $e$. Para isso, precisamos introduzir agora a função logarítmica natural, ou função logarítmica de base e. Vamos relembrar um pouquinho dos logaritmos.
Seja $a > 0$, $a\neq 1$. Diremos que $y = \log_a(x)$ se $a^y=x$. Isto é, $y$ é o logaritmo de x na base a se $y$ é o expoente que precisamos dar ao número $a$ para que a potência $a^y$ resulte em $x$.
Alguns exemplos:
$\log_2(8) = 3$, pois $2^3=8$, isto é, 3 é o expoente que o 2 precisa para se tornar 8.
$\log_4(2)=\frac{1}{2}$, pois $4^{\frac{1}{2}} = \sqrt{4} = 2$.
$\log_a(1) = 0$, pois $a^0=1$, para todo $a>0$.
$\log_2\left(\frac{1}{2}\right)=-1$, pois $2^{-1}=\frac{1}{2}$ .
Uma população de bactérias cresce a uma taxa proporcional à população presente. Sabendo-se que após uma hora a população é 2 vezes a população inicial, determine a população como função do tempo e o tempo necessário para que a população triplique.
Já vimos que a população $y(t)$ é dada por $y(t)= C\cdot 2^t$, pois o valor dobra a cada passagem de uma hora. Precisamos calcular o tempo necessário para que a população triplique, isto é $y(t)=3C$. Então $3C=C\cdot 2^t$, logo $3=2^t$ e, com isso, $t = \log_2(3)$. Relembrando as propriedades de mudança de base, podemos ainda escrever $t = \log_2(3) =\dfrac{\ln(3)}{\ln(2)}$. Uma calculadora nos dará $t\approx 1,58 \ horas \approx$ 1h e 35 min.
Note que só podemos calcular $\log_a(x)$ quando $x > 0$, pois $\log_a(x) = y$ é o mesmo que $a^y = x$ e, como $a>0$, teremos necessariamente $x>0$.
Um fato importante é que, para qualquer $a>0$, $a\neq 1$, e para todo $x > 0$,
\begin{equation}\tag{3} a^{\log_a(x)} = x.\end{equation}Consegue entender por quê? Ora, $\log_a(x)$ é o expoente que precisamos dar ao $a$ para que ele se torne $x$, então, dando este expoente ao $a$... ele se tornará $x$! A identidade acima será muito utilizada em vários momentos deste curso.
Como $e$ é um número positivo diferente de 1, podemos naturalmente pensar no $\log$ com base $e$, que denotaremos $\log_e$ ou ainda $\ln$. Com esta notação, por exemplo, $\ln(1) = 0$, pois $e^0=1$; $\ln(e^a)=a$, pois $e^a=e^a$, $\ln(1/e) = -1$, pois $e^{-1}=\frac{1}{e}$; e assim por diante. Outro fato importante é que, pela
identidade 3,
De maneira ainda mais geral, $e$ elevado ao $\ln$ de qualquer coisa é a própria qualquer coisa. Por exemplo, se esta qualquer coisa for uma função,
\[e^{\ln\left(f(x)\right)} = f(x).\]O logaritmo em base $e$ é tão especial que, além da notação $\ln$, há muitos autores que o representam simplesmente por $\log$, especialmente em textos da área de Análise Matemática. Como também é comum se utilizar $\log$ para a exponencial em base 10, especialmente em textos mais voltados a aplicações, utilizaremos apenas $\ln$ ou $\log_e$, sendo este último apenas para fins didáticos, quando quisermos relembrar que $\ln$ é um $\log$ de base $e$.
Já estamos em condição de tentar obter uma derivada para uma função exponencial $f(x) = a^x$, com qualquer $a>0$. Pela igualdade 4, temos
\[a = e^{\ln(a)}.\]Assim,
\[f(x) = a^x = \left(e^{\ln(a)}\right)^x = e^{\ln(a)\cdot x} = \exp\left(x\ln(a)\right).\]Podemos então derivar $f$ utilizando a Regra da Cadeia.
\begin{eqnarray*}f'(x) &=& \left[\exp\right(\ln(a)\cdot x\left)\right]'\\ &=& \exp\left(\ln(a)\cdot x\right)\cdot \left[\ln(a)\cdot x\right]' \\&=& \exp\left(\ln(a)\cdot x\right)\cdot \ln(a) \\&=& e^{\ln(a)\cdot x}\cdot\ln(a)\\&=& \left(e^{\ln(a)}\right)^x\cdot\ln(a)\\&=& a^x\cdot\ln(a)\\&=&\ln(a)\,a^x\end{eqnarray*}Note que, nas contas acima, utilizamos que $\exp' = \exp$ e que $\left[\ln(a)\cdot x\right]' = \ln(a)$, pois $\ln(a)$ é uma constante. Assim,
\[\left(a^x\right)' = \ln(a)\,a^x.\]Vamos derivar $f(x)=x^\pi+\pi^x+\pi^\pi, \ \ x>0$.
Usando que $(a^x)' = \ln(a)\,a^x$, temos $(\pi^x)'=\ln(\pi)\,\pi^x$. Observe que $\pi^\pi$ é uma constante e que a derivada de $x^\pi$ é feita utilizando a regra da potência, pois o expoente $\pi$ é constante. Logo
$$f'(x)=\pi x^{\pi-1}+\ln(\pi)\,\pi^x+0=\pi x^{\pi-1}+\ln(\pi)\,\pi^x.$$A Derivada da Função Logarítmica
Na seção anterior, dados $a > 0$, $a\neq 1$ e $x>0$, definimos que $y = \log_a(x)$ se $a^y=x$, ou seja, o logaritmo de x na base a é o expoente $y$ que precisamos dar ao número $a$ para que a potência $a^y$ resulte em $x$. Se definirmos a função exponencial de base $a$ por $f(x) = a^x$, temos então que $y=\log_a(x)$ se e somente se $x=f(y)$. Assim, a função
\[\log_a: (0,+\infty) \to \mathbb{R}\]é a função inversa de
\[f: \mathbb{R} \to (0,+\infty),\]isto é, $\log_a = f^{-1}$.
Note ainda que
\[\left(f\circ \log_a\right) (x) = a^{\log_a(x)} = x,\] \[\left(\log_a \circ f\right) (x) = \log_a(f(x)) = \log_a\left(a^x\right) = x\cdot \log_a(a) = x\cdot 1 = x,\]ou seja, o que a exponencial faz, o $\log$ desfaz, e vice-versa.
O caso mais interessante é quando a base é igual a $e$. Neste caso, temos a exponencial $\exp(x) = e^x$ e a função logarítmica $\ln = \log_e$. Pelo que vimos acima, $\ln = \exp^{-1}$ e $\exp = \ln^{-1}$ (uma função é a inversa da outra).
Com isso, podemos aplicar o Teorema da Função Inversa, que vimos nas seções anteriores. Se $y=e^x$, este Teorema nos garante que
\[\ln '(y) = \frac{1}{\exp'(x)} = \frac{1}{e^x} = \frac{1}{y}\;,\]logo,
\[\ln'(y) = \frac{1}{y}.\]Escrevendo com $x$, que é o mais comum, temos que
\[\ln'(x) = \frac{1}{x}.\]Vamos agora obter a derivada da função logarítmica com uma base $a>0$ qualquer. Podemos fazer isto de duas formas. A primeira delas é repetir o argumento acima, isto é, se $y=a^x$, denotando $f(x)=a^x$, temos que $\log_a = f^{-1}$ e, portanto, pelo TFI,
\[\log_a'(y) = \frac{1}{f'(x)} = \frac{1}{\ln(a) a^x} = \frac{1}{\ln(a)\cdot y}\;,\]logo
\[\log_a'(x)=\frac{1}{\ln(a)\cdot x}.\]Outra forma de obtermos o mesmo resultado é através da mudança de base no logaritmo:
\[\log_a(x) = \frac{\log_e(x)}{\log_e(a)} = \frac{\ln(x)}{\ln(a)},\]logo
\[\log_a'(x) = \left(\frac{\ln(x)}{\ln(a)}\right)' = \frac{1}{\ln(a)} \ln'(x) = \frac{1}{\ln(a)}\cdot\frac{1}{x} = \frac{1}{\ln(a)\cdot x}.\]Seja $f(x)=\log_2(e^{-x}\mathrm{sen}(x))$ e vamos calcular $f'(x)$.
Usando que $\log_2'(x)=\dfrac{1}{\ln(2)\cdot x}$ e a regra da cadeia obtemos
$$f'(x)=\dfrac{1}{\ln(2)\cdot e^{-x}\mathrm{sen}(x)}\cdot (e^{-x}\mathrm{sen}(x))'.$$Usando a regra do produto $(e^{-x}\mathrm{sen}(x))'=-e^{-x}\mathrm{sen}(x)+e^{-x}\cos(x)$ e logo
$$f'(x)=\frac{1}{\ln(2)\cdot e^{-x}\mathrm{sen}(x)}\cdot[-e^{-x}\mathrm{sen}(x)+e^{-x}\cos(x)]=\frac{1}{\ln(2)}\left[\frac{-e^{-x}\mathrm{sen}(x)}{e^{-x}\mathrm{sen}(x)}+\frac{e^{-x}\cos(x)}{e^{-x}\mathrm{sen}(x)}\right]$$ $$=\frac{1}{\ln(2)}[-1+\mathrm{cotg}(x)].$$ Derivar a função definida por $f(x)=x^x$, com $x>0$.
Embora esta função tenha uma expressão simples, ela não se encaixa nas regras elementares de derivação. Ela não é uma potência, por exemplo, pois o expoente não é constante. Tampouco é uma exponencial, pois a base não é constante.
Podemos escrever
\[x = e^{\ln(x)},\]logo
\[f(x) = x^x = \left(e^{\ln(x)}\right)^x = e^{x\,\ln(x)}.\]Derivando, temos
\[f'(x) = \left(e^{x\,\ln(x)}\right)'=e^{x\,\ln(x)} \cdot \left(x\,\ln(x)\right)'=e^{x\,\ln(x)} \cdot \left(\ln(x) + x \cdot \frac{1}{x}\right) = e^{x\,\ln(x)} \cdot \left(\ln(x) + 1\right).\]Como $e^{x\,\ln(x)} = x^x$, temos
\[f'(x) = x^x \left(\ln(x) + 1\right) = x^x\,\ln(x) + x^x.\]Derivação Logarítmica
Quando queremos derivar funções muito complexas, envolvendo produtos, quocientes, potências e exponenciais, as regras de derivação podem se tornar muito difíceis de aplicar. Veremos agora um processo um pouco mais simples, que chamaremos de derivação logarítmica.
Derivar a função dada por $f(x) = \dfrac{e^{x^2} \sqrt{x^2+1}}{\left(2x+1\right)^3}$, com $x>-\dfrac{1}{2}$.
Já pensou ter que aplicar todas as regras de derivação necessárias? Regra do produto, do quociente, da cadeia, derivada de potência, de exponencial... é trabalho para três dias!
Quando $f(x)>0$, podemos, por outro lado, escrever
\[\ln(f(x)) = \ln\left(\dfrac{e^{x^2} \sqrt{x^2+1}}{\left(2x+1\right)^3}\right).\]Agora, com as propriedades do logaritmo, podemos simplificar o lado direito, obtendo
\begin{eqnarray*}\ln(f(x)) &=& \ln\left(\dfrac{e^{x^2} \sqrt{x^2+1}}{\left(2x+1\right)^3}\right)\\ \\&=& \ln\left(e^{x^2}\right) + \ln\left(\sqrt{x^2+1}\right) - \ln\left(\left(2x+1\right)^3\right)\\ \\&=&x^2 + \frac{1}{2}\ln(x^2+1) - 3\, \ln(2x+1),\end{eqnarray*}logo
\[\ln(f(x)) = x^2 + \frac{1}{2}\ln(x^2+1) - 3\,\ln(2x+1).\]e agora derivar em relação a $x$, obtendo
\[\frac{1}{f(x)}\cdot f'(x) = 2x + \frac{1}{2} \cdot \frac{1}{x^2+1} \cdot (x^2+1)' - 3 \cdot \frac{1}{2x+1}\cdot (2x+1)',\]logo
\[\frac{f'(x)}{f(x)} = 2x + \frac{1}{2} \cdot \frac{1}{x^2+1} \cdot 2x - 3 \cdot \frac{1}{2x+1}\cdot 2,\]ou ainda
\[\frac{f'(x)}{f(x)} = 2x + \frac{x}{x^2+1} - \frac{6}{2x+1}.\]Assim,
\[f'(x) = f(x)\left(2x + \frac{x}{x^2+1} - \frac{6}{2x+1}\right) = \dfrac{e^{x^2} \sqrt{x^2+1}}{\left(2x+1\right)^3}\left(2x + \frac{x}{x^2+1} - \frac{6}{2x+1}\right).\]Derivar a função definida por $f(x)=x^x$, com $x>0$.
Já derivamos esta função na seção anterior, mas vamos derivar novamente, desta vez utilizando derivação logarítmica.
Aplicando $\ln$ aos dois lados,
\[\ln(f(x)) = \ln(x^x),\]logo
\[\ln(f(x)) = x\,\ln.(x)\]Derivando, temos
\[(\ln(f(x)))' = (x\,\ln(x))',\]logo
\[\frac{f'(x)}{f(x)} = x'\,\ln(x) + x\,\ln'(x) = \ln(x) + x\cdot\frac{1}{x},\]portanto
\[\frac{f'(x)}{f(x)} = \ln(x) + 1.\]Com isso
\[f'(x)= f(x)\,\ln(x) + f(x) = x^x\,\ln(x) + x^x.\]Nestes exemplos, seguimos os seguintes passos:
- Aplicamos o $\ln$ aos dois lados da expressão de $f(x)$.
- Utilizamos as propriedades do logaritmo para simplificar a expressão obtida do lado direito (se não conseguirmos simplificar, não fará muito sentido utilizarmos este método)
- Derivamos os dois lados (no lado esquerdo, teremos $\frac{f'(x)}{f(x)}$)
- Isolamos $f'(x)$ passando o $f(x)$ multiplicando para o lado direito.
Derivar a função $f(x) = e^{x^x}$, com $x>0$.
Vamos proceder por derivação logarítmica. Temos
\[\ln\left(f(x)\right) = \ln\left(e^{x^x}\right) = x^x = \left(e^{\ln(x)}\right)^x = e^{x\,\ln(x)}.\]Derivando $\ln(f(x)) = e^{x\,\ln(x)}$ dos dois lados,
\begin{eqnarray*}\left(\ln\left(f(x)\right)\right)' &=& \left(e^{x\,\ln(x)}\right)' \\\frac{1}{f(x)}\cdot f'(x) &=& e^{x\,\ln(x)} \cdot \left(x\ln(x)\right)' \\\frac{f'(x)}{f(x)} &=& e^{x\,\ln(x)} \cdot \left(1\cdot\ln(x) + x \cdot \frac{1}{x}\right) \\\frac{f'(x)}{f(x)} &=& e^{x\,\ln(x)} \cdot \left(\ln(x) + 1\right) \\f'(x)&=& f(x)\cdot e^{x\,\ln(x)} \cdot \left(\ln(x) + 1\right) \\f'(x)&=& e^{x^x}\cdot e^{x\,\ln(x)} \cdot \left(\ln(x) + 1\right) \\f'(x)&=& e^{x^x}\cdot x^x \cdot \left(\ln(x) + 1\right) \\\end{eqnarray*}Um pouco mais sobre o número $e$
Esta seção pode ser lida como uma curiosidade apenas, ou mesmo ser omitida em uma primeira leitura.
Sabemos que a derivada de $\ln(x)$ é $\dfrac{1}{x}$, assim,
\begin{eqnarray*}1 = \frac{1}{1} = \ln'(1) &=& \lim_{h\to 0} \frac{\ln(1+h)-\ln(1)}{h}\\&=& \lim_{x\to 0} \frac{\ln(1+x)-\ln(1)}{x}\\&\overset{*}{=}& \lim_{x\to 0} \frac{\ln(1+x)}{x}\\&=& \lim_{x\to 0} \frac{1}{x}\cdot\ln\left(1 + x\right)\\&\overset{**}{=}& \lim_{x\to 0} \ln\left((1 + x)^{\frac{1}{x}}\right)\\\end{eqnarray*}(em (*) utilizamos que $\ln(1)=0$, em (**) utilizamos $a\cdot\ln(b) = \ln(b^a)$).
Como a função exponencial $f(x)=e^x$ é contínua em $x=1$, e como $\lim_{x\to 0} \ln\left((1 + x)^{\frac{1}{x}}\right) = 1$ temos que
\[e = e^1 = f(1) = f\left(\lim_{x\to 0} \ln\left((1+x)^{\frac{1}{x}}\right)\right) = \lim_{x \to 0} f\left(\ln\left((1 + x)^{\frac{1}{x}}\right)\right) = \lim_{x \to 0} e^{\ln\left( (1 + x)^{\frac{1}{x}}\right)} = \lim_{x \to 0} \left(1 + x\right)^{\frac{1}{x}}\]Assim,
\[e = \lim_{x \to 0} \left(1 + x\right)^{\frac{1}{x}}.\]Fazendo $n=1/x$, quando $x\to 0^+$, teremos que $n\to +\infty$. Assim,
\[e = \lim_{n \to +\infty}\left(1+\frac{1}{n}\right)^n.\]Como já foi visto nas seções anteriores, outra forma interessante de explorar o número $e$ é aproximar a função exponencial $\exp(x)=e^x$ por Polinômios de Taylor em torno do ponto $x_0=0$. O Polinômio de Taylor de ordem $n$ em $x_0=0$, é dado por
\[p(x) = \exp(0) + \exp'(0) \cdot (x-0) + \frac{\exp''(0)}{2!}(x-0)^2 + \frac{\exp'''(0)}{3!}(x-0)^3 + ... + \frac{\exp^{(n)}(0)}{n!}(x-0)^n.\]Sabemos que $\exp'(x) = \exp(x)$, logo
\[\exp''(x) = \left(\exp'(x)\right)' = \exp(x),\] \[\exp'''(x) = \left(\exp''(x)\right)' = \exp(x),\] \[\vdots\] \[\exp^{(n)}(x) = \left(\exp^{(n-1)}(x)\right)' = \exp(x),\]ou seja, as derivadas de todas as ordens da exponencial de base $e$ são iguais à própria exponencial. Assim,
\[1 = \exp(0) = \exp'(0) = \exp''(0) = ... = \exp^{(n)}(0).\]Com isso, o Polinômio de Taylor em torno de $x_0=0$ pode ser escrito como
\begin{eqnarray*}p(x) &=& 1 + (x-0) + \frac{(x-0)^2}{2!} + \frac{(x-0)^3}{3!} + ... + \frac{(x-0)^n}{n!}\\&=& 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^n}{n!}.\end{eqnarray*}Tomando $x=1$, temos
\[p(1) = 1 + 1 + \frac{1}{2!} = \frac{1}{3!} + ... + \frac{1}{n!}.\]Como, por definição, $0! = 0$ e $1! = 1$, temos
\[p(1) = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + ... + \frac{1}{n!}.\]Já vimos que o erro na aproximação do Polinômio de Taylor acima, isto é, a diferença entre $e=\exp(1)$ e $p(1)$ é dado por $\frac{\exp^{(n+1)}(c)}{(n+1)!}$, para algum $0 \leq c \leq 1$. Como $\exp^{(n+1)}(c) = \exp(c) = e^c < e^1$, temos que o erro é menor que $e/(n+1)!$. Ou seja, se escolhermos um valor muito grande para $n$, a soma
\[\frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + ... + \frac{1}{n!}\]será uma excelente aproximação para $e$. Se quisermos uma aproximação ainda melhor, tão boa quanto precisarmos, basta tomar um $n$ ainda maior. Isto significa que $e$ pode ser dado pela soma de infinitas parcelas
\[e = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + ... + \frac{1}{n!} + ...\]Se voltarmos ao Polinômio de Taylor $p(x)$, vemos ainda que $e^x$ pode ser dado por
\[e^x = \frac{1}{0!} + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^n}{n!}+...\]
Somas infinitas podem parecer estranho, mas você já as viu quando estudou Progressões Geométricas, no Ensino Médio. Aqui, temos algo semelhante, uma soma cujas parcelas vão muito rapidamente para 0, tão rápido que fazem a soma convergir, embora não seja uma progressão geométrica.
Há um fato bem interessante relacionado a esta expressão de $e^x$ como soma infinita. Vamos assumir que podemos derivar a soma infinita termo a termo, como podemos fazer com uma soma de finitas funções. Não é imediato que a possamos fazer isso, na verdade, precisamos de muito arroz com feijão matemático para garantir que é possível, e mesmo assim, apenas sob certas hipóteses. Mas, ok, supondo que possamos derivar, teremos
\begin{eqnarray*}(e^x)' &=& \left(\frac{1}{0!}\right)' + \left(\frac{x}{1!}\right)' + \left(\frac{x^2}{2!}\right)' + \left(\frac{x^3}{3!}\right)' + ... + \left(\frac{x^n}{n!}\right)'+...\\&=& 0 + \frac{1}{1!} + \frac{2x^1}{2!} + \frac{3x^2}{3!} + \frac{4x^3}{4!}... + \frac{nx^{n-1}}{n!}+\frac{(n+1)x^{n}}{(n+1)!}+...\\&=& 0 + \frac{1}{1!} + \frac{\cancel{2}x^1}{\cancel{2}\cdot 1!} + \frac{\cancel{3}x^2}{\cancel{3} \cdot 2!} + \frac{\cancel{4}x^3}{\cancel{4} \cdot 3!}... + \frac{\cancel{n}x^{n-1}}{\cancel{n} \cdot (n-1)!}+ \frac{\cancel{(n+1)}x^n}{\cancel{n+1} \cdot n!}++...\\&=&\frac{1}{0!} + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + ... + \frac{x^n}{n!}+...\\&=&e^x,\end{eqnarray*}mostrando que esta expressão se comporta muito bem com relação à derivada, nos levando ao esperado $(e^x)' = e^x$.

