Curvas Definidas por mais de uma Função
A curva $x-y^2=0$ é uma parábola invertida, como mostra o gráfico abaixo. Não é gráfico de uma função de $x$, mas podemos descrevê-la usando duas funções, $y=\sqrt{x}$, $x\geq 0$ , que descreve a parte superior (azul) e $y=-\sqrt{x}$, $x\geq 0$, que descreve a parte inferior (magenta).
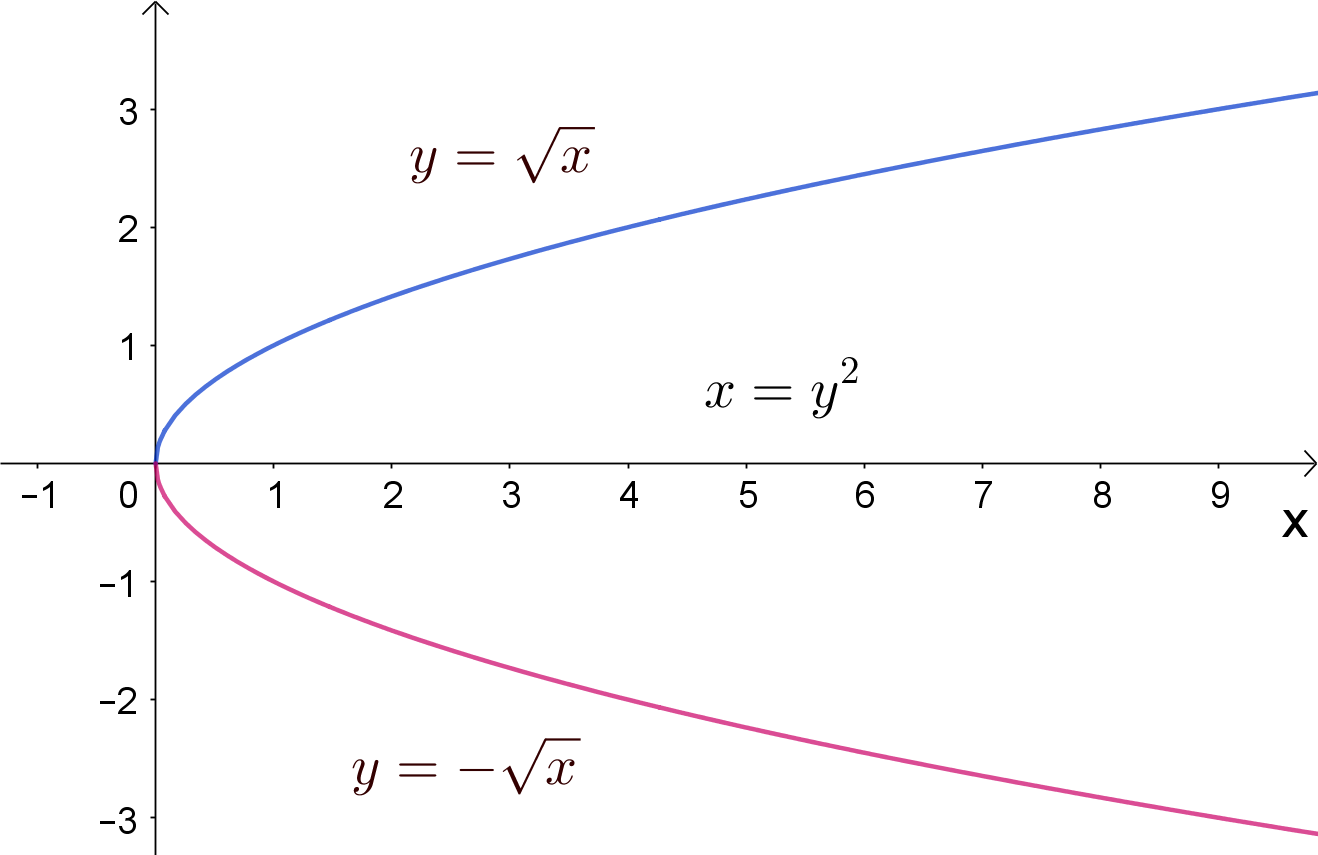
A parábola invertida
$x-y^2=0$.
A circunferência $x^2+y^2=r^2$, onde $r>0$ é o raio, também não é gráfico de uma função de $x$, mas podemos descrevê-la usando duas funções, $y=\sqrt{r^2-x^2}$, $-r\leq x\leq r$, que descreve a parte superior (azul) e $y=-\sqrt{r^2-x^2}$, $-r\leq x\leq r$, que descreve a parte inferior (magenta).

Circunferência de raio $r$:
$x^2+y^2=r^2$.
Dependendo da situação, também podemos usar a variável $y$ como variável independente. Nesse caso, podemos formular o Teste da reta horizontal para verificar se uma curva é gráfico de uma função de $y$.
Considere a curva $x^2+y^2=1$, para $-1\leq y\leq 1 $ e $0\leq x\leq 1$.
- Como posso descrevê-la usando $x$ como variável?
- Como posso descrevê-la usando $y$ como variável?
- [(a)] Observe que $y^2=1-x^2\Rightarrow y=\sqrt{1-x^2}$ ou $y=-\sqrt{1-x^2}$, para $0\leq x\leq1$. Assim, podemos descrever a semicircunferência usando duas funções de $x$, a saber, $y=\sqrt{1-x^2}$, $0\leq x\leq1$ para a parte de cima (azul) e $y=-\sqrt{1-x^2}$, $0\leq x\leq1$ para a parte de baixo (magenta).

Semicrcunferência de raio 1:
$x^2+y^2=1$, $0\leq x\leq19$.. - [b)] Observe que $x^2=1-y^2\Rightarrow x=\sqrt{1-y^2}$, para $-1\leq y\leq1$, pois $x\geq0$. Assim, podemos descrever a semicircunferência usando uma única função de $y$, a saber, $f(y)=\sqrt{1-y^2}$, $-1\leq y\leq1.$

