Parte do conteúdo desta seção é apresentado no vídeo "Funções Trigonométricas"
Funções Trigonométricas
Você consegue se lembrar das razões trigonométricas no triângulo retângulo?
Estas razões estão definidas para um ângulo de medida .
Há três ângulos cujas razões trigonométricas são muito especiais, , e .
Considerando o quadrado de lado da figura à esquerda e traçando sua diagonal , temos e . Assim,
Considerando o triângulo equilátero de lado da figura à esquerda, traçando sua altura , temos e . Assim, olhando para o ângulo ,
Olhando agora para o ângulo ,
Hoje, você verá que estas razões trigonométricas podem ser estendidas à funções de domínio . Para isso, precisaremos sair de um triângulo retângulo, onde os ângulos são limitados ao domínio .
Também deixaremos de trabalhar com os ângulos medidos em graus e adotaremos uma forma mais natural de expressar ângulos, que, na verdade, passarão a ser arcos.
O Círculo Trigonométrico
Você poderá experimentar os conceitos desta seção e da próxima no applet abaixo:
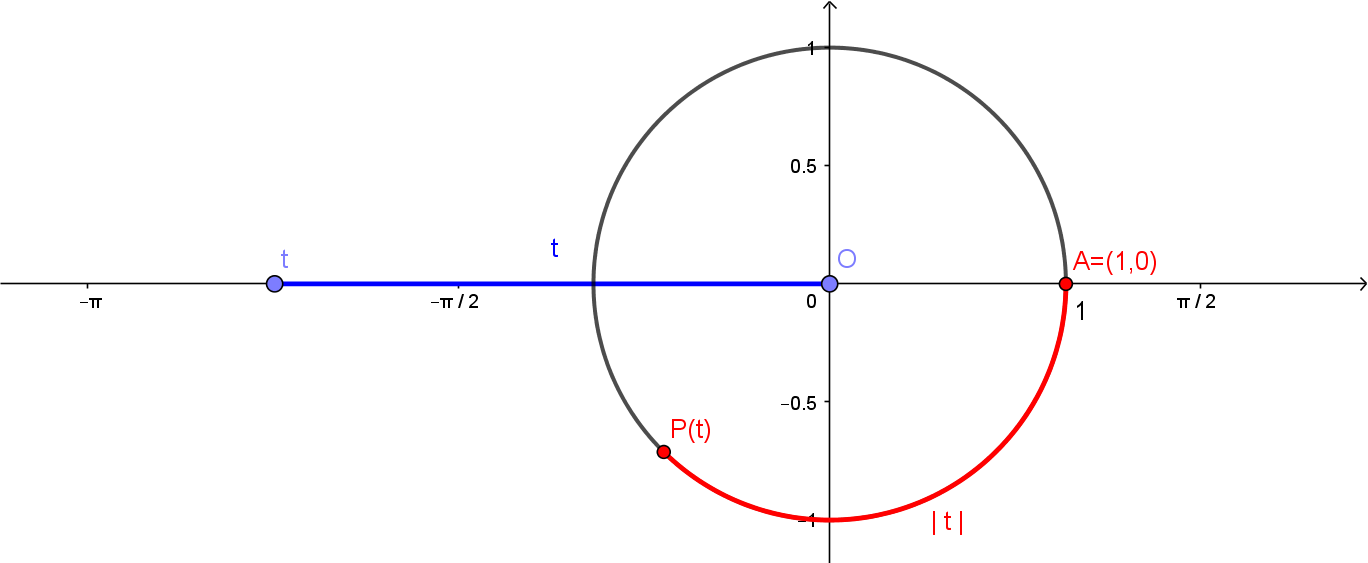
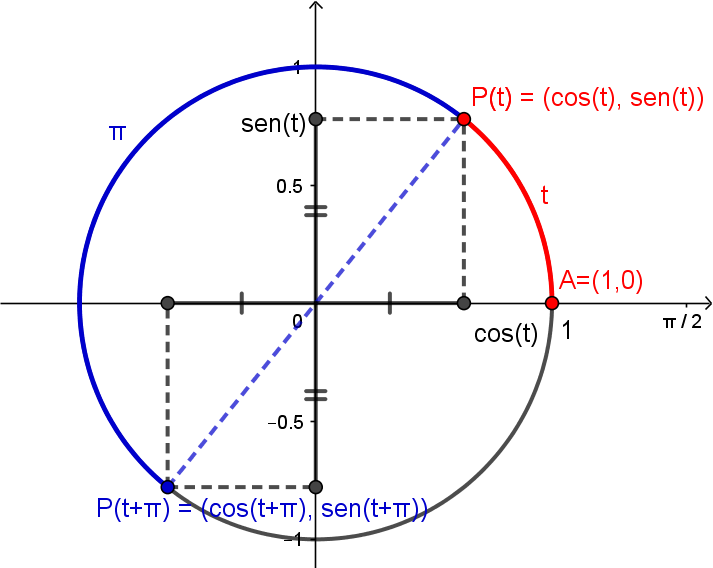
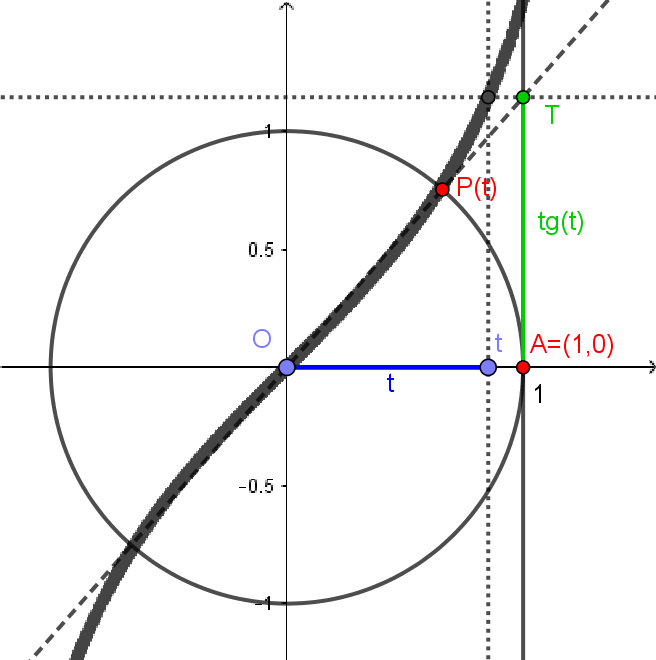
Vamos inciar considerando o círculo de centro em e raio 1, da figura abaixo. Considere também o ponto .
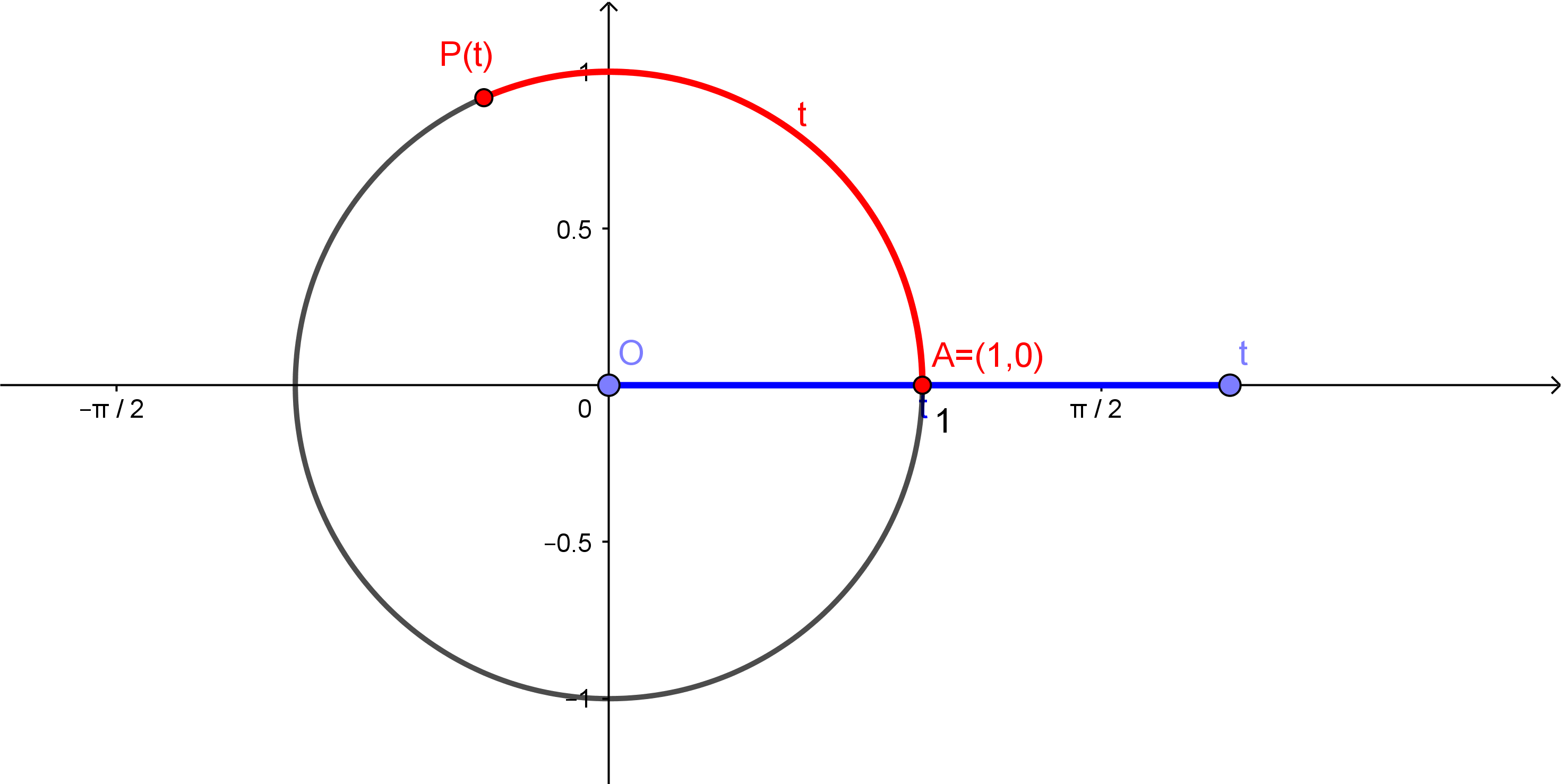
Escolha agora um número real . O comprimento do segmento de extremos e , esboçado abaixo em azul, é . Considere, sobre o círculo, o arco de comprimento , desenhado a partir de e percorrendo o círculo no sentido anti-horário, como na figura abaixo. Chame de o outro extremo deste arco.
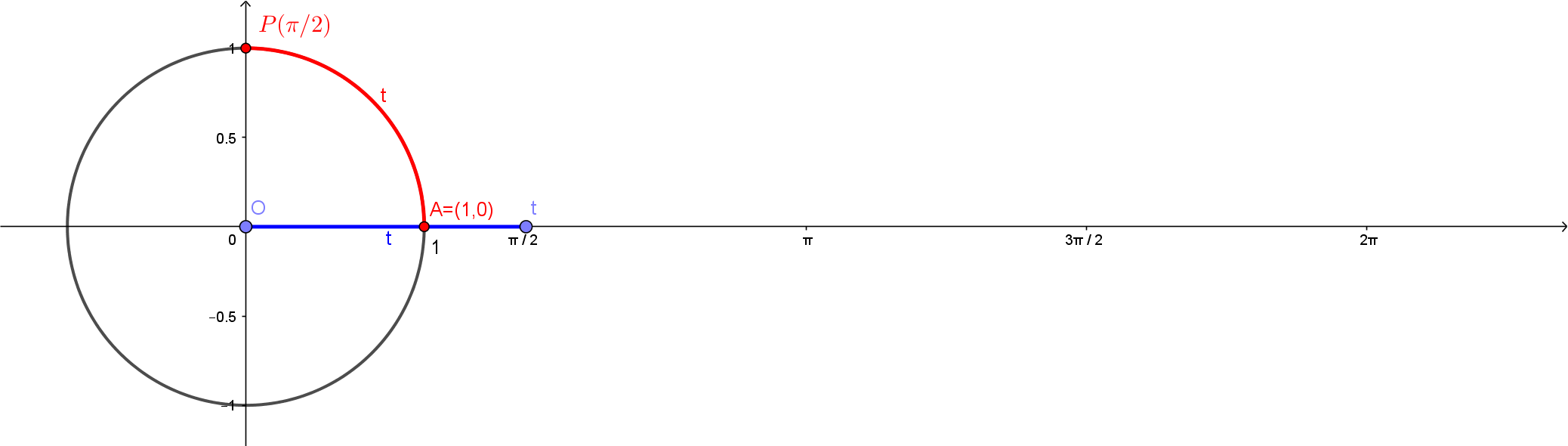
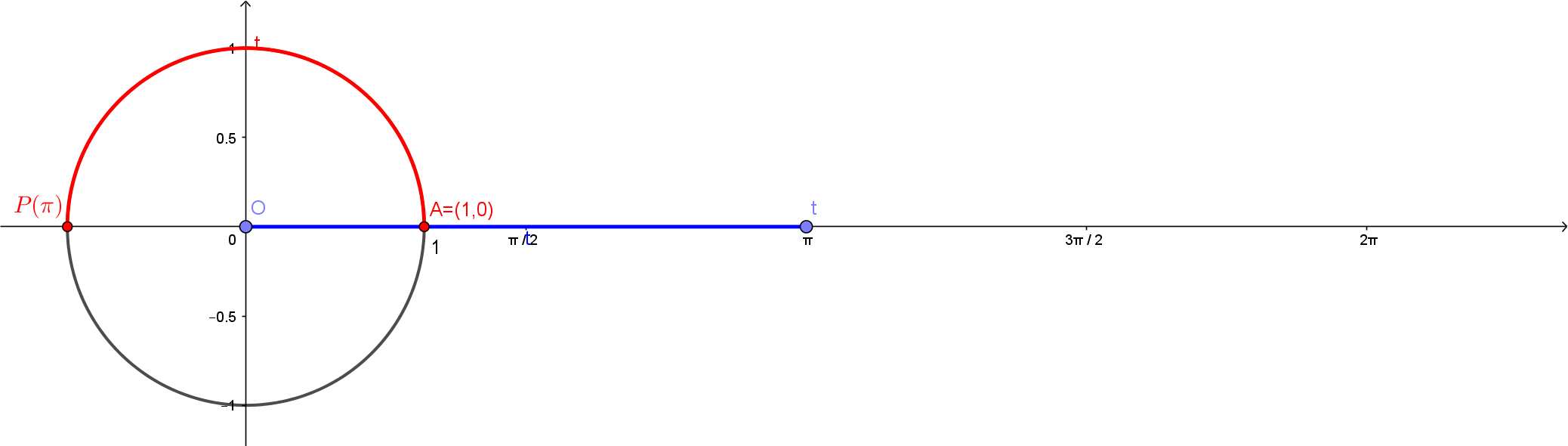
Uma observação importante é que como o raio deste círculo é , o comprimento deste círculo inteiro será dado por . Com isso, temos nas figuras abaixo os pontos , , e .
Também podemos ter . Neste caso, será percorrido um arco de comprimento , também a partir de , porém no sentido horário.
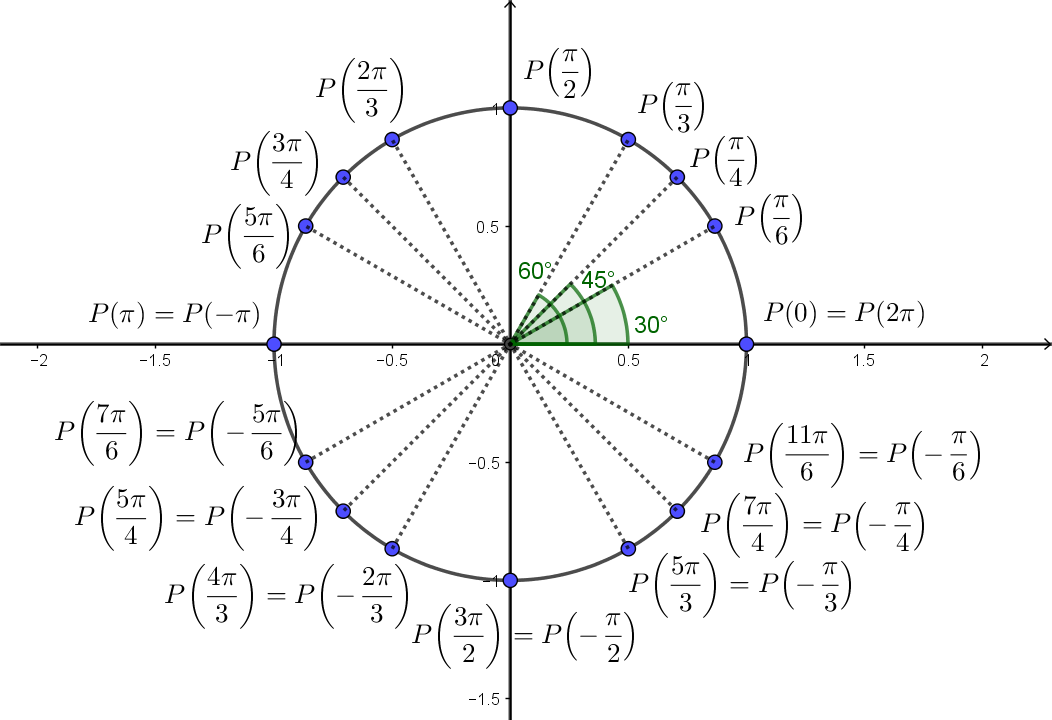
Na figura abaixo, destacamos alguns pontos interessantes.
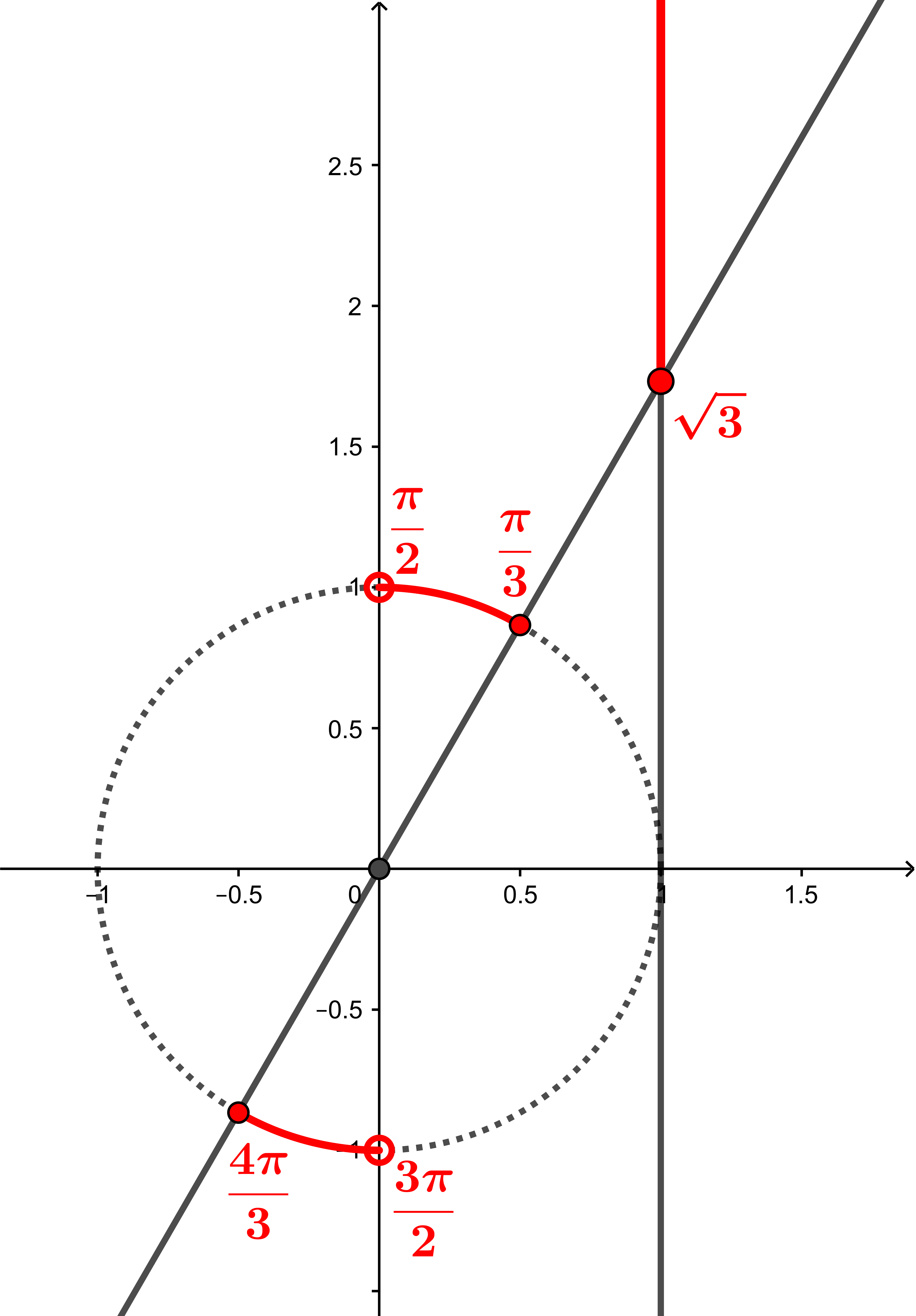
Para marcar alguns destes pontos, lembre corresponde ao círculo inteiro, logo corresponde a meio círculo, a um quarto, a um sexto e a um doze-avos.
Alguns pontos foram escritos como correspondentes a mais de um valor de . Na verdade, todos poderiam ter sido escritos assim. Podemos chegar a qualquer ponto do círculo partindo de e percorrendo o círculo no sentido horário ou anti-horário. Na verdade, cada ponto pode ser atingido percorrendo o círculo com infinitos arcos diferentes, basta ficarmos dando muitas voltas.
Cada volta completa no círculo, seja no sentido horário ou anti-horário, nos levará ao mesmo ponto de partida. Assim, todos os arcos de comprimento , com inteiro, percorridos a partir de nos levam... de volta ao próprio ponto . Assim, para todo ,
De maneira geral, se a diferença entre o comprimento de dois arcos é um número inteiro de voltas, isto é, se eles têm comprimentos e , com , os arcos terminarão no mesmo lugar, isto é,
Seno e Cosseno de
Você poderá experimentar os conceitos desta seção e da anterior no applet abaixo:
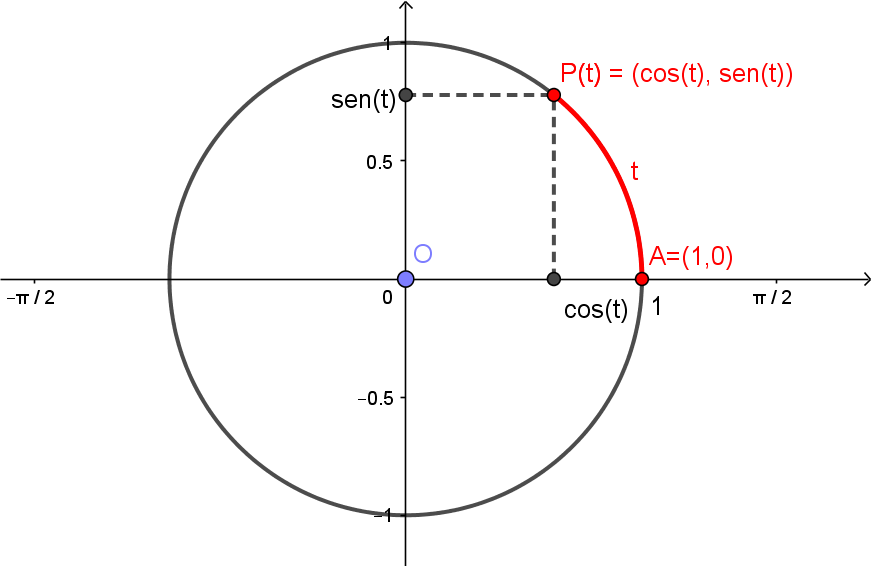
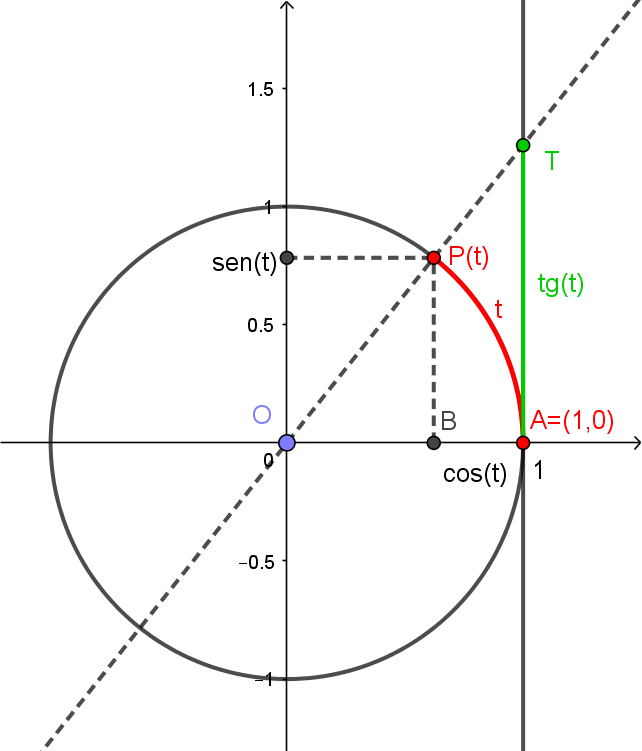
Considerando o número real e o ponto correspondente a ele, como vimos na seção anterior, definimos o cosseno e seno de respectivamente por
Isto é, e são tais que
Como as coordenadas de são e , e como sabemos que este círculo é o conjunto dos pontos satisfazendo , teremos então
ou, como é mais comum escrever
que é chamada de relação trigonométrica fundamental.
Podemos também observar que, como o raio do círculo é 1,
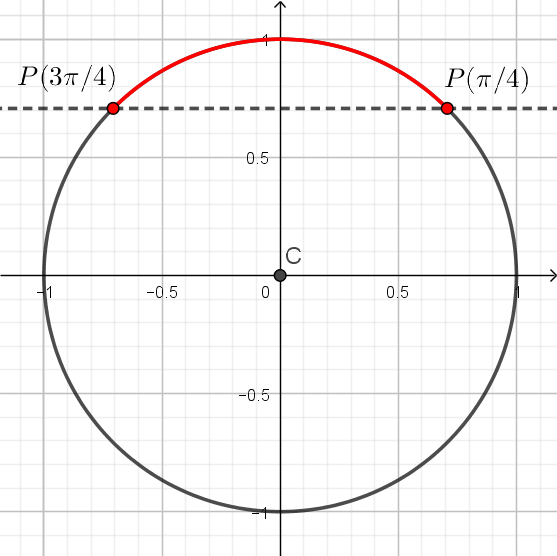
Observando os pontos do primeiro quadrante, e os ângulos centrais de , , e que formam, vemos que
Observando agora os pontos , , e , temos
Já vimos que , logo
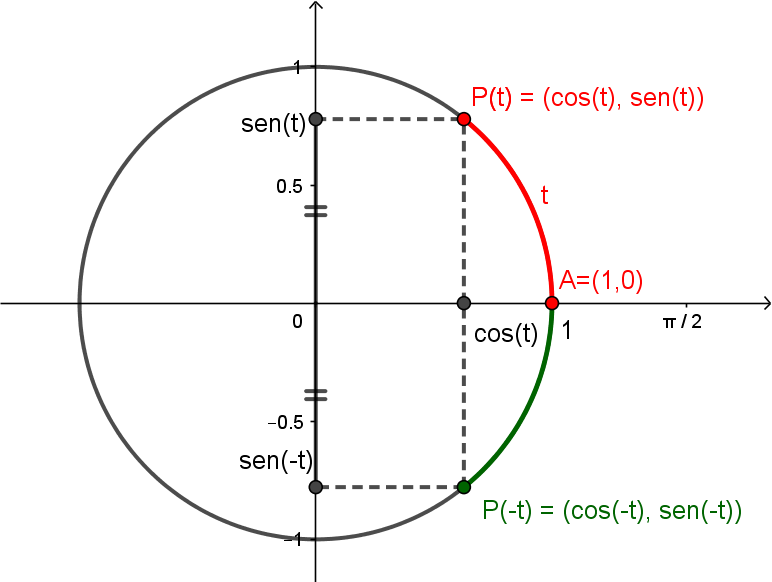
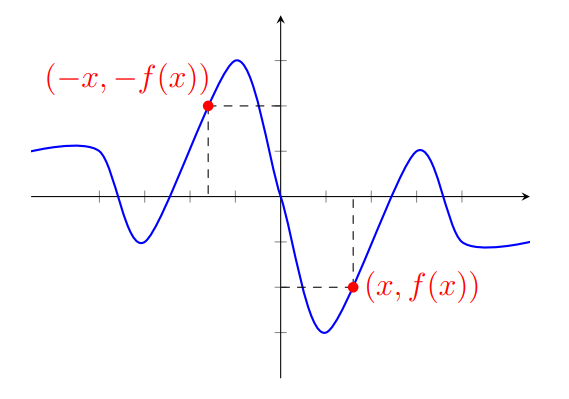
Na figura abaixo, você pode ver que os pontos e são simétricos em relação ao eixo , pois são atingidos percorrendo arcos de mesmo tamanho, porém em direções opostas.
As coordenadas destes pontos serão as mesmas, logo
As coordenadas destes pontos serão simétricas, logo
A diferença entre os arcos correspondentes a e é de , que corresponde a meia volta no círculo. Portanto, os pontos e são simétricos, como podemos ver na figura abaixo.
Logo,
Algumas Relações Importantes
Duas relações muito importante, mas que não demonstraremos aqui, são as que nos dão seno e cosseno da soma de dois arcos:
Há pessoas que gostam também de "decorar" outras duas relações, para a diferença entre dois arcos. Mas nós não precisamos, pois elas seguem como consequência do que já vimos:
Na verdade, as pessoas gostam muito de "decorar fórmulas", o que é bem estranho...
Seguindo aplicando as relações da soma de arcos para , temos ainda que
Outra relação muito importante, também decorrente da relação da soma do seno, é que
ou seja,
Portanto, o cosseno de tem exatamente o mesmo valor que o seno assumirá em um arco maior que .
Exemplo 1
Calcule .
logo
A chave neste exemplo é perceber que . Mas como perceber isso? Pode ajudar se você pensar em graus:
As Funções Seno e Cosseno
Para cada , definimos na seção anterior e . Assim, temos duas funções e , com algumas propriedades que já deduzimos na sessão anterior.
Proposição 1
As funções e satisfazem às seguintes propriedades
, ou seja, o cosseno é uma função par.
, ou seja, o seno é uma função ímpar.
e , ou seja, cosseno e seno são funções periódicas, com período .
e .
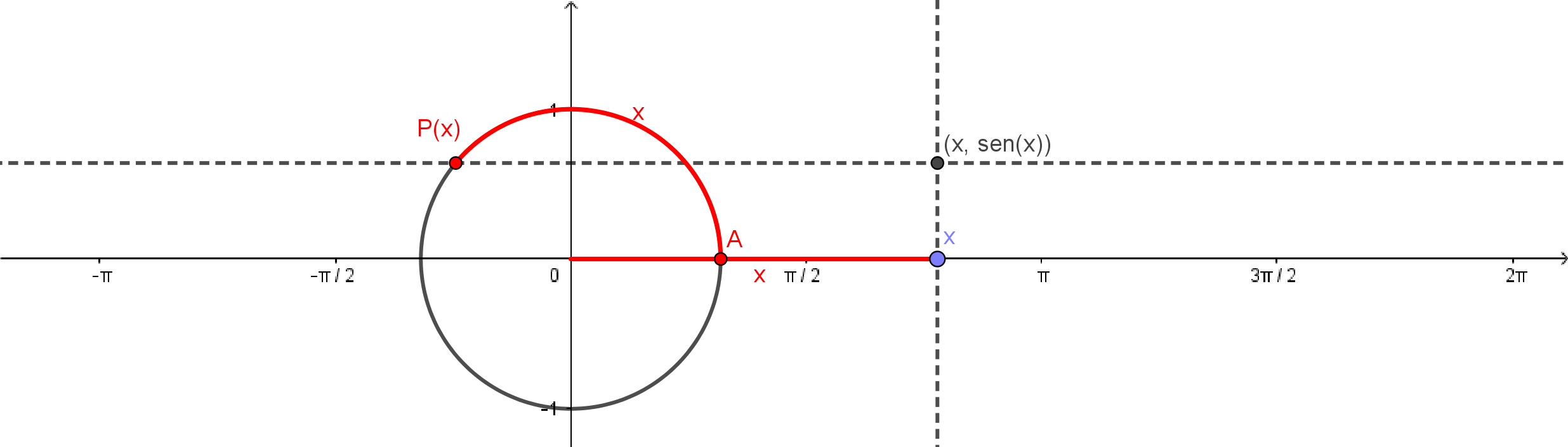
O gráfico de é o conjunto dos pontos da forma . Podemos construir este gráfico a partir da definição do seno. Para , consideramos o ponto correspondente no círculo, que terá coordenadas . O ponto do gráfico, possui, portanto a mesma coordenada que , estando portanto na mesma reta horizontal. Mas este ponto também está na mesma reta vertical que , logo, é a interseção das retas que passam por e .
Você pode experimentar uma construção do gráfico, como acima, no applet abaixo:
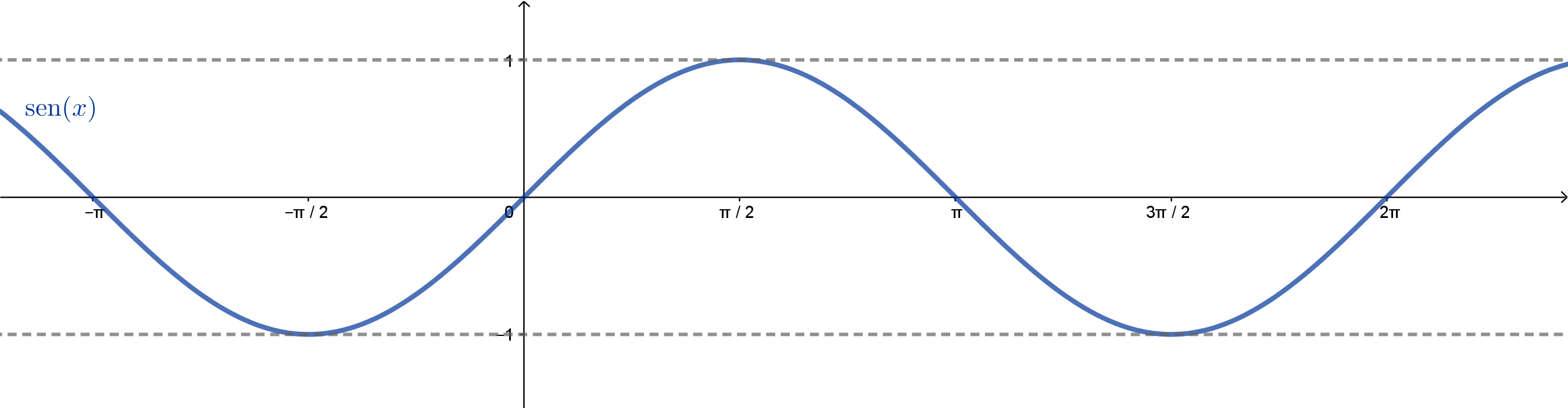
Abaixo, temos o gráfico do seno construído desta forma:
Observe que os valores máximo e mínimo são 1 e e que as raízes são os pontos da forma , com . Já vimos que o cosseno de tem exatamente o mesmo valor que o seno assumirá em um arco maior que . Por exemplo, teremos , , etc. Se estivéssemos falando do estudo de um fenômeno, no qual é o tempo, poderíamos dizer que o cosseno "acontece" segundos antes do seno. Com isso, seu gráfico é o mesmo do seno, apenas "antecipado" de unidades em .
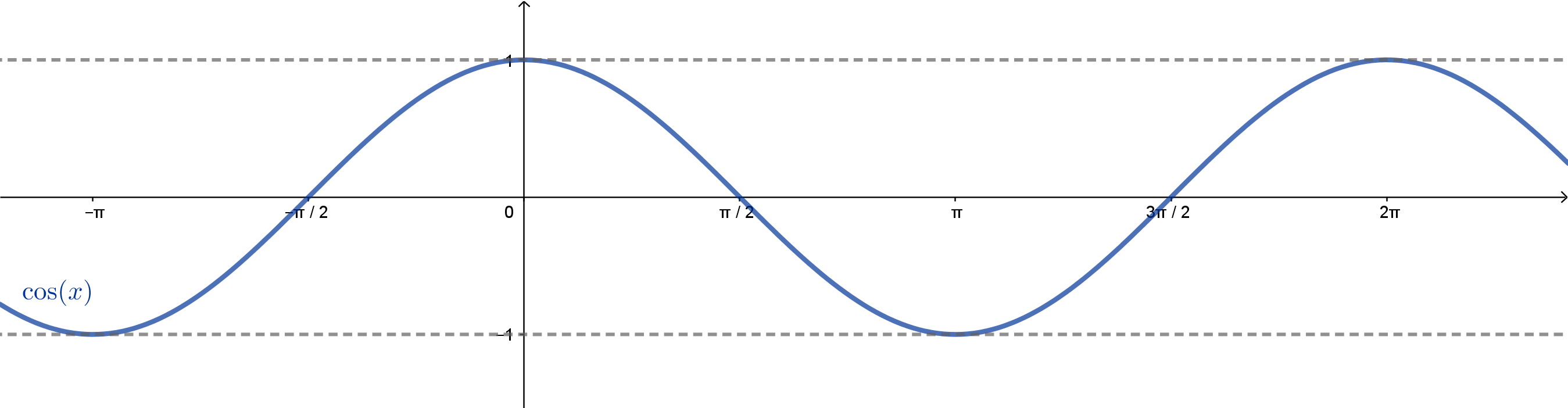
Na próxima seção, veremos que o gráfico do cosseno é obtido por uma translação no gráfico do seno.
Exemplo 2
Determine os valores de para os quais
Há apenas dois pontos no círculo cuja coordenada horizontal (o cosseno) é igual a . O primeiro destes pontos é o correspondente ao arco de (que corresponde ao ângulo central de ). O outro ponto, com a mesma coordenada horizontal, é o simétrico ao primeiro com relação ao eixo . Este ponto é o correspondente ao arco de .
Assim, a equação é satisfeita por e por , mas estes não são os únicos valores de que tornam válida a igualdade. Qualquer outro valor ou , com , corresponderá a um dos dois pontos do círculo acima, logo também terão cosseno igual a .
Assim,
Exemplo 3
Determine os valores de para os quais
Há apenas dois pontos no círculo cuja coordenada vertical (o seno) é igual a . Estes pontos são os correspondentes aos arcos de e o .
Como o seno é dado pela coordenada vertical de um ponto do círculo, os pontos cujo seno é maior ou igual a são aqueles acima da reta ou na reta. O conjunto destes pontos estão representados na figura abaixo:
Estes pontos correspondem aos arcos de comprimento . Assim,
Porém, estes não são os únicos arcos que satisfazem a desigualdade. Qualquer arco de comprimento com , com , também corresponderá a um dos pontos destacados na figura (serão dadas voltas e depois percorrido um arco que terá extremo no conjunto destacado). Assim,
As Funções Tangente e Cotangente
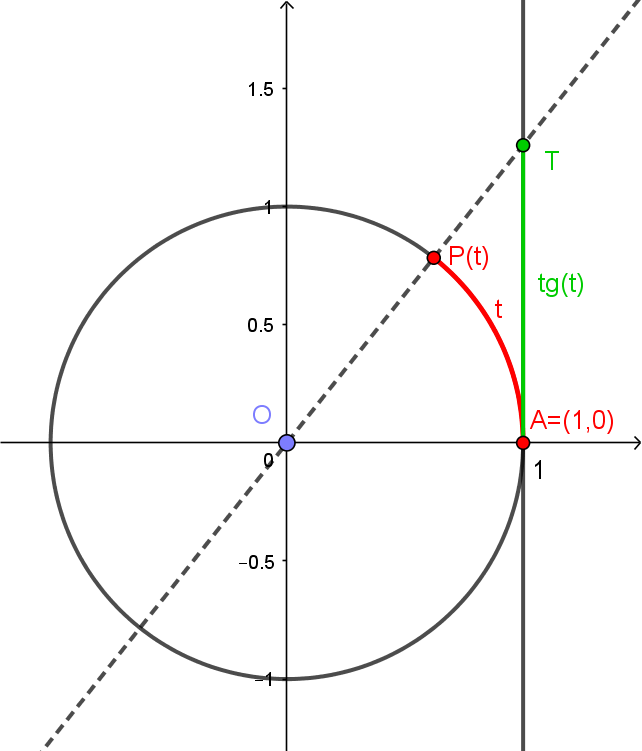
Agora, vamos considerar a reta , tangente ao círculo. Dado , tomamos o ponto , como antes. A reta que passa por e cortará a tangente em um ponto . Definiremos a tangente de , representada por , como sendo a coordenada do ponto . Veja abaixo.
Você pode experimentar uma construção da tangente e seu gráfico no applet abaixo:
Pela semelhança entre os triângulos retângulos e da figura abaixo, temos
Um detalhe sobre a tangente é que ela não está definida para todo . Se, por exemplo, , o ponto estará sobre o eixo e, portanto, a reta não intersectará a reta , portanto não existirá o ponto e a tangente. Isto acontecerá sempre que estiver sobre o eixo , ou seja, quando for ou mais geralmente, qualquer valor da forma , com . Isto é, quando for mais qualquer número de mais-voltas.
E, como as equações não mentem jamais, a expressão que deduzimos para a tangente, , também não está definida para tais valores de , pois, para na forma , , teremos .
Assim, a tangente determina uma função real de domínio dado por , isto é, uma função
Podemos construir o gráfico da da mesma forma que foi feito com o .
O gráfico da tangente é como abaixo. Repare que suas raízes são as mesmas da função e que ela não está definida para os valores de nos quais .
Proposição 2
A função tem as seguintes propriedades:
, ou seja, é uma função ímpar.
, quando estiver definida.
, logo é uma função de período .
Podemos concluir estas propriedades a partir do que já sabemos sobre as funções seno e cosseno. Temos
e ainda,
Com esta relação, e lembrando que , deduzimos a terceira propriedade:
Exemplo 4
Se , quais são as possibilidades para e ?
Como
e, como
temos
logo
e então
Com isso,
Assim,
Se , temos
Se, por outro lado, , temos
Assim, temos duas possibilidades
Exemplo 5
Determine todos os valores de tais que
Como , vemos, no círculo trigonométrico, que se, e somente se,
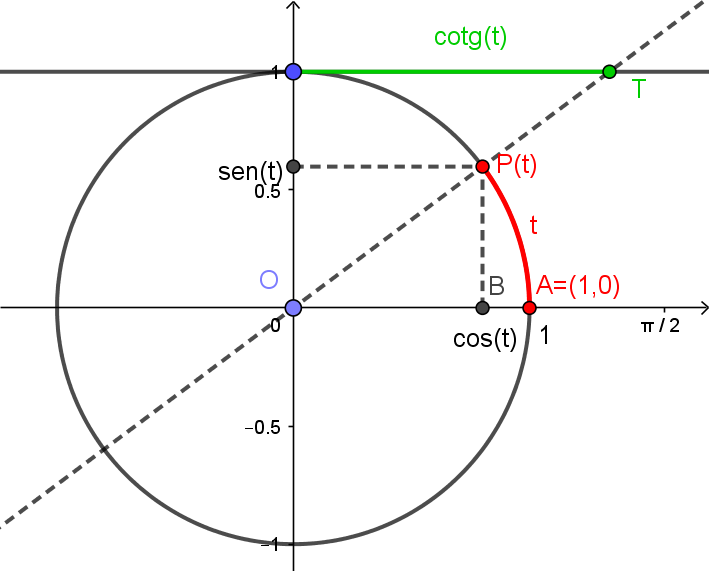
De forma semelhante à tangente, definimos a cotangente de , denotada por . Na figura abaixo, é a coordenada do ponto .
Procedendo como na tangente, através da semelhança de triângulo, podemos concluir que
definida quando não for da forma , com . Teremos então a função real
A cotangente tem as propriedades semelhantes à tangente:
Proposição 3
A função tem as seguintes propriedades:
, ou seja, é uma função ímpar.
, logo é uma função de período .
O gráfico da função é dado abaixo.
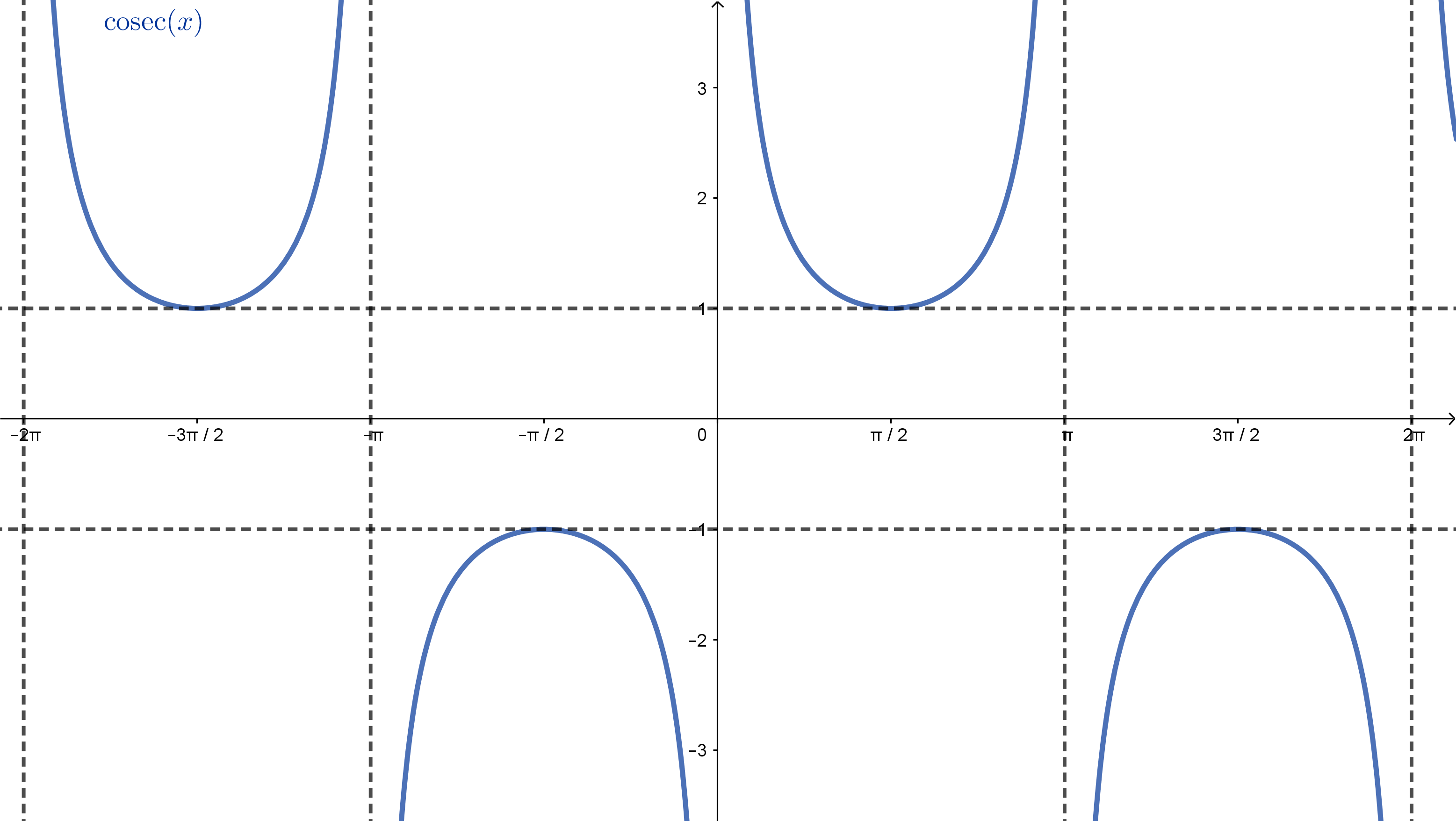
As funções secante e cossecante
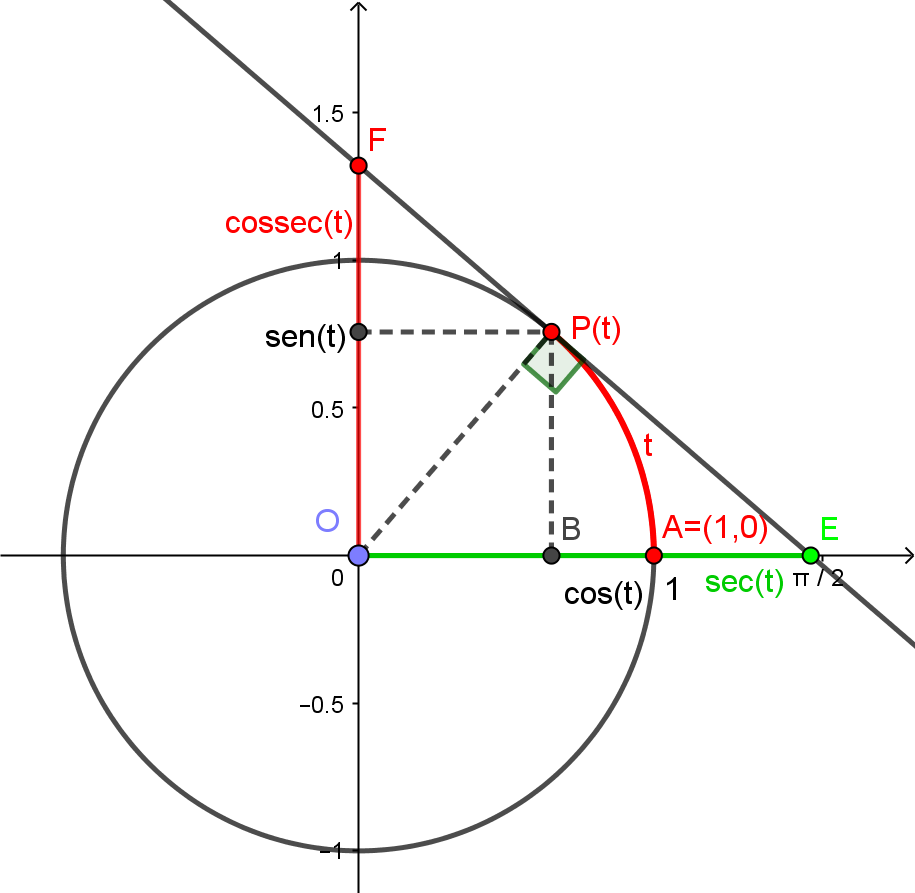
Considere agora uma reta tangente ao círculo no ponto e os pontos e de interseção desta reta com os eixos e , respectivamente, como na figura abaixo.
Definimos a secante e a cossecante de como sendo, respectivamente, a coordenada do ponto e a coordenada do ponto . A partir da semelhança entre os triângulos e , concluímos que
e que está definida sempre que para todo . A partir da semelhança entre os triângulos e , concluímos que
e que está definida sempre que para todo .
Temos então as funções reais
Proposição 4
A função tem as seguintes propriedades:
, ou seja, é uma função par.
, logo é uma função de período .
ou para todo
O gráfico da função é dado abaixo.
Proposição 5
A função tem as seguintes propriedades:
, ou seja, é uma função par.
, logo é uma função de período .
ou para todo
O gráfico da função é dado abaixo.
Observe que
logo, como para todo onde está definido, temos
ou seja, ou . Da mesma forma, , ou seja, ou .