Nas seções anteriores, foram apresentadas algumas funções elementares e seus gráficos. Agora pretendemos apresentar como podemos obter novas funções mais elaboradas, recorrendo à composição de funções. Vejamos um exemplo onde temos uma aplicação da composição de funções.

Exemplo 1

Suponha que recebeu um vale de $R $ 40$ para gastar numa livraria. A função que descreve o valor a pagar usando o vale é $f (x) = x - 40$ . Mas no dia que escolhe ir à livraria, eles estão oferecendo um desconto de $30 %$ em todos os livros de cálculo. A função que descreve o desconto desse dia é $g (x) = x - 0, 3 x = 0, 7 x$ . A livraria permite deixar o cliente escolher qual a ordem para aplicar o desconto, ou seja você deve escolher entre considerar a função custo $f \circ g$ ou $g \circ f$ .

Note que $(f \circ g) (x) = f (0, 7 x) = 0, 7 x - 40$ e $(g \circ f) (x) = g (x - 40) = 0, 7 (x - 40) = 0, 7 x - 28$ .

Então o comprador deve escolher a opção de custo dada por $f \circ g$

Dadas duas ou mais funções podemos combiná-las usando diversas operações, obtendo novas funções.

Se considerarmos duas funções

f

g

podemos por exemplo definir as funções

f + g

f - g

f g

f / g

que correspondem à soma, subtração, produto e quociente de funções, respectivamente. Além destas operações, podemos também usar a composição de funções. A composição de duas funções consiste em aplicar uma das funções e depois aplicar a outra função à imagem obtida após a aplicação da primeira função. Ou seja, dadas duas funções

f

g

, podemos aplicar

g

a um certo valor de

x

(pertencente ao domínio de

g

e depois aplicar

f

g (x)

, caso

g (x)

esteja no domínio de

f

Definição 1

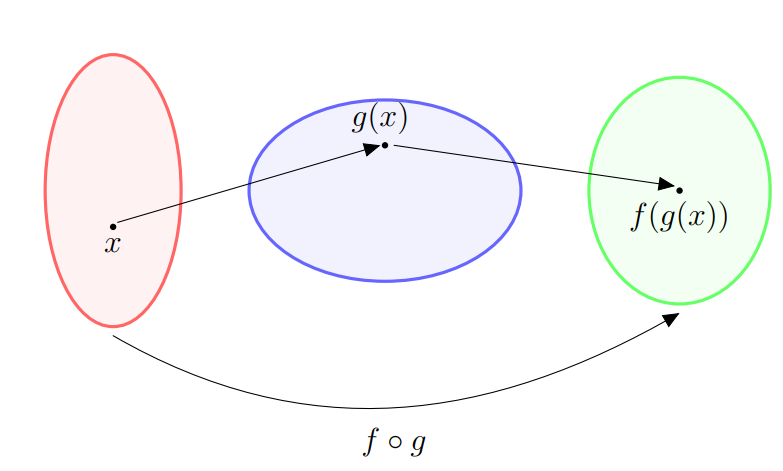
Dadas duas funções $f$ e $g$ , a função composta $f \circ g$ é definida por

(f \circ g) (x) = f (g (x)),

sendo o seu domínio o conjunto $D (f \circ g) = {x \in D (g) : g (x) \in D (f)}$ .

Também podemos denominar

f \circ g

por composição de

f

g

. O esquema abaixo ilustra a definição da composição

f \circ g

Observação: A operação composição de funções não é comutativa, ou seja, em geral

f \circ g

é diferente de

g \circ f

. Por exemplo, se para

x \in R

considerarmos

f (x) = x^{2}

g (x) = x + 3

, então

(f \circ g) (x) = f (x + 3) = (x + 3)^{2}

(g \circ f) (x) = g (x^{2}) = x^{2} + 3

, ambas com domínio

R

Exemplo 2

A função $h (x) = \sqrt{1 + x^{2}}$ é a composição das funções $f (x) = \sqrt{x}$ e $g (x) = 1 + x^{2}$ , ou seja, $h = f \circ g$ . Observe que a $I m (g) = [1, \infty)$ está contida em $D (f) = [0, + \infty)$ , logo $D (f \circ g) = D (g) = R$ .

Exemplo 3

A função $h (x) = \frac{1}{2 + | x |}$ é a composição das funções $f (x) = \frac{1}{x}$ , $x \neq 0$ e $g (x) = 2 + | x |$ , $x \in R$ , ou seja, $h = f \circ g$ . Observe que a $I m (g) = [2, \infty)$ que está contido $D (f) = R - {0}$ , portanto $D (f \circ g) = R$ .

Nem sempre é possível escolher duas funções ao acaso e tentar determinar a composição das duas. Para que a função

f \circ g

esteja bem definida é necessário que a imagem de

g

esteja contida no domínio de

f

, ou seja

I m (g) \subset D (f)

Exemplo 4

Consideremos as funções $f (x) = \sqrt{x}$ e $g (x) = - x^{4}$ . Neste caso, $f \circ g$ não está definida em $R$ (que é o domínio de $g$ ), pois a $I m (g) = (- \infty, 0]$ e $D (f) = [0, + \infty)$ portanto $f \circ g$ estaria definida apenas em $x = 0$ .

Exemplo 5

Consideremos as funções

\begin{array}{ccccc} \begin{array}{cccc} f : & R & \to & [- 4, + \infty) \\ x & \mapsto & x^{2} - 4 \end{array} & e & \begin{array}{cccc} g : & [0, + \infty) & \to & R \\ x & \mapsto & \sqrt{x} \end{array} \end{array}

Para determinarmos o domínio de $g \circ f$ precisamos considerar os valores de $x$ tais que $f (x)$ pertença ao domínio de $g$ , ou seja, serão os valores tais que $x^{2} - 4 \geq 0$ , ou seja, $x \in (- \infty, - 2] \cup [2, + \infty)$ . Nesse caso a função $g \circ f$ está definida por $(g \circ f) (x) = g (f (x)) = g (x^{2} - 4) = \sqrt{x^{2} - 4}$ .

Composição de Funções