
Algumas funções podem ser apresentadas verbalmente, isto é, usando apenas palavras, sem expressões matemáticas. Nesse caso, devemos encontrar a expressão matemática que define a função descrita verbalmente, esse processo é um exemplo simples do que chamamos de modelagem matemática. Para isso, fazemos um esboço do problema, através de desenhos, listagem das variáveis envolvidas e em muitos casos encontramos uma ou mais equações matemáticas que relacionem as variáveis.
Um retângulo tem área igual a 25 $m^2$.
Uma escada com 3$m$ de comprimento está apoiada em uma parede vertical. Se a base da escada desliza, afastando-se da parede, determine a distância da base da escada à parede em função da distância da base da parede ao topo da escada.
Sejam $x$ a distância da base da escada à parede e $y$ a distância do topo da escada ao chão, como na figura a seguir:
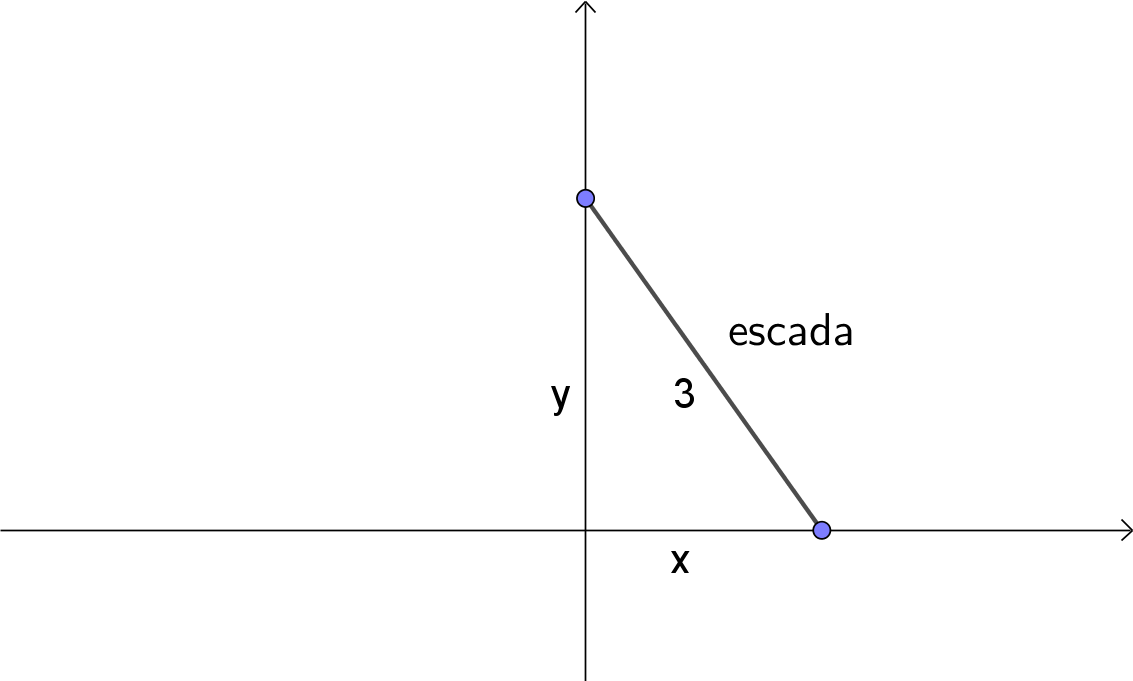
Usando o Teorema de Pitágoras, temos que $x^2+y^2=9$, portanto a distância $x$ da base da escada à parede em função da distância $y$ da base da parede ao topo da escada é dada por $x=\sqrt{9-y^2}$, para $0\leq y\leq 3$.