
Antes de começarmos, vamos relembrar (a jato!) algumas propriedades básicas de potências, que serão úteis mais à frente. Caso não tenha familiaridade com alguma delas, não é precisa memorizar; deixe esta lista perto de você para eventuais consultas.
Para $a>0$, $b>0$, $x \in \mathbb{R}$, $y \in \mathbb{R}$, valem as propriedades
Não faremos aqui uma demonstração das propriedades acima, por não ser o objetivo deste texto. Muitas das propriedades também são válidas quando $a$ ou $b$ forem negativos, porém algumas deixariam de valer, como a (iv), outras precisariam ser adaptadas ou ganhar hipóteses adicionais até mesmo para estarem bem definidas, como a (ii) e (vii) e a (viii), por exemplo. Por isso, nos limitamos apenas ao caso $a>0$ e $b>0$, que será o único necessário neste texto.
Imagine uma cultura de bactérias, inicialmente com 1.000.000 indivíduos e crescendo a uma mesma razão em intervalos de tempo fixados, de forma que esta população dobre a cada 1 hora, enquanto não houver restrição de nutrientes ou interferência que dificulte este crescimento.
Vamos considerar o tempo do início da observação como $t=0$. Enquanto não houver alguma interferência, teremos um crescimento como abaixo:
| $t$ | 0 | 1 | 2 | 3 | 4 | 5 |
| População | 1.000.000 | 2.000.000 | 4.000.000 | 8.000.000 | 16.000.000 | 32.000.000 |
A cada hora, a população será o dobro da anterior. A partir disso, podemos obter uma expressão para a população $P$ em função de $t$, quando $t$ for um inteiro não-negativo.
| $P(0)$ | $=$ | $1.000.000$ | $=$ | $1.000.000 \cdot 1$ | = | $1.000.000$ | $\cdot$ | $2^0$ | |
| $P(1)$ | $=$ | $2.000.000$ | $=$ | $\left(1.000.000 \cdot 2^0\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^1$ | |
| $P(2)$ | $=$ | $4.000.000$ | $=$ | $\left(1.000.000 \cdot 2^1\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^2$ | |
| $P(3)$ | $=$ | $8.000.000$ | $=$ | $\left(1.000.000 \cdot 2^2\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^3$ | |
| $P(4)$ | $=$ | $16.000.000$ | $=$ | $\left(1.000.000 \cdot 2^3\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^4$ | |
| $P(5)$ | $=$ | $32.000.000$ | $=$ | $\left(1.000.000 \cdot 2^4\right)\cdot 2$ | = | $1.000.000$ | $\cdot$ | $2^5$ | |
| $\vdots$ | |||||||||
| $P(t)$ | $=$ | $(1.000.000\cdot 2^{t-1}) \cdot 2$ | $=$ | $1.000.000$ | $\cdot$ | $2^t,$ | para $t \in \mathbb{N}$ |
Estes valores nos dão o esboço abaixo:

Porém, esta cultura de bactérias não dá ``saltos populacionais", o crescimento é gradual ao longo do tempo. Qual seria, por exemplo, a população de bactérias quando $t=1/2$, isto é, meia hora após iniciarmos a observação?

Em cada período de meia hora ($1/2$ hora), a população de bactérias cresce um mesmo fator, que vamos chamar de $a$. Assim, a população $P(1/2)$ meia hora após o início do experimento é igual à população inicial multiplicada por $a$. Da mesma forma a população $P(1)$ é igual à população de meia hora antes multiplicada por $a$, ou seja, $a\cdot P(1/2)$. Lembrando ainda que $P(1) = 2\cdot P(0)$,
\[\left\{ \begin{array}{rcl} P(1/2) &=& a\cdot P(0)\\ P(1) &=& a\cdot P(1/2)\\ P(1) &=& 2\cdot P(0)\\ \end{array} \right. \]Substituindo o $P(1)$ da terceira igualdade por $a\cdot P(1/2)$ (dado pela segunda igualdade), temos
\[2\cdot P(0) = a\cdot P(1/2)\]e, substituindo $P(1/2)$ acima por $a\cdot P(0)$ (dado pela primeira igualdade), temos
\[2\cdot P(0) = a\cdot \left(a\cdot P(0)\right).\]Assim,
\[2\cdot P(0) = a^2 \cdot P(0),\] logo $a^2 = 2$ e, portanto $a = \sqrt{2}$ ou $a=-\sqrt{2}$. Como o valor negativo não faz sentido no problema, temos $a = \sqrt{2} =2^{1/2}$.
Com isso, a população após meia hora de observação, é dada por
E qual seria a população de bactérias, por exemplo, quando $t=1/n$?
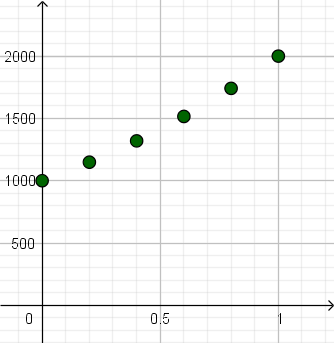
Assim como fizemos acima, em cada período de $1/n$ hora, a população de bactérias cresce um mesmo fator $b$. Logo a população em cada múltiplo de $1/n$ hora é a população de $1/n$ hora atrás multiplicada por $b$:
\[ \left\{ \begin{array}{rcl} P(1/n) &=& b\cdot P(0)\\ P(2/n) &=& b\cdot P(1/n)\\ P(3/n) &=& b\cdot P(2/n)\\ &\vdots& \\ P(1) = P(n/n) &=& b\cdot P((n-1)/n)\\ \end{array} \right. \]A primeira igualdade nos dá $P(1/n) = b\cdot P(0)$ que, substituindo na segunda, dá $P(2/n) = b^2 P(0)$. Substituindo este $P(2/n)$ na terceira, temos $P(3/n) = b^3P(0)$. Seguindo assim, chegaremos na última igualdade com $P(1) = P(n/n) = b^n P(0)$. Como $P(1) = 2\cdot P(0)$, temos
\[2\cdot P(0) = b^n\cdot P(0),\] logo $b^n = 2$ e, portanto, $b = \sqrt[n]{2} =2^{1/n}$. (Quando $n$ é par, a equação $b^n = 2$ também admitiria a solução $b = -\sqrt[n]{2}$, que descartamos por não fazer sentido no fenômeno que estamos estudando)
Temos então
Temos também
\[P(2/n) = b\cdot P(1/n) = 2^{1/n}\cdot (1.000.000 \cdot 2^{1/n}) = 1.000.000 \cdot 2^{2/n},\]e, prosseguindo assim,
\[P(3/n) = b\cdot P(2/n) = 2^{1/n}\cdot (1.000.000 \cdot 2^{2/n}) = 1.000.000 \cdot 2^{3/n}.\]\[P(4/n) = b\cdot P(3/n) = 2^{1/n}\cdot (1.000.000 \cdot 2^{3/n}) = 1.000.000 \cdot 2^{4/n}.\]
\[\vdots\]
\[P(m/n) = b\cdot P\left(\frac{m-1}{n}\right) = 2^{1/n}\cdot 1000 \cdot 2^{\frac{m-1}{n}} = 1.000.000\cdot 2^{m/n},\]
para todo $m \in \mathbb{N}$. E qual teria sido a população de bactérias, por exemplo, uma hora antes de a observação começar, isto é, quando $t=-1$?

Em cada período de 1 hora, a população de bactérias dobra, portanto a população $P(0)$ no começo da observação é o dobro da população $P(-1)$ de uma hora antes. Logo,
\[P(0) = 2 \cdot P(-1),\]e então
\[\therefore P(-1) = \frac{P(0)}{2} = P(0)\cdot 2^{-1} = 1.000.000\cdot 2^{-1}.\]Repetindo os argumentos feitos para $m, n \in \mathbb{N}$, podemos concluir que
\[P(-n) = 1.000.000 \cdot 2^{-n},\]
\[P(-m/n) = 1.000.000 \cdot 2^{-m/n}.\]
Até aqui, já concluímos então que, para todo número racional $t= m/n \in \mathbb{Q}$, temos
\[P(t) = 1.000.000\cdot 2^t.\] Esta expressão pode ser estendida a todos os valores de $t \in \mathbb{R}$. Para isso, consideramos aproximações racionais $q$ cada vez melhores de $t$ e veremos o valor de $P(q)$ se aproximar do valor que será o de $P(t)$. Esta é apenas uma forma intuitiva de pensar, que ficará mais clara apenas à frente do curso, quando estudarmos limites e continuidade.
Para todo $t \in \mathbb{R}$, temos então
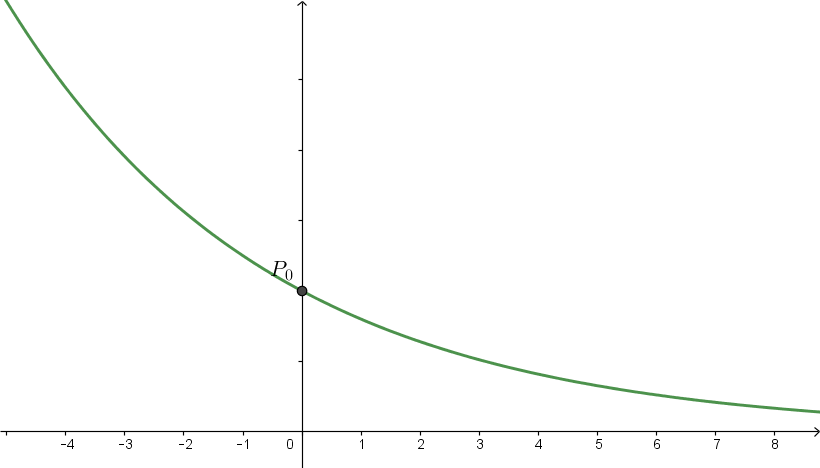
O gráfico da função dada $P: \mathbb{R} \rightarrow \mathbb{R}$ dada por esta expressão é como abaixo.
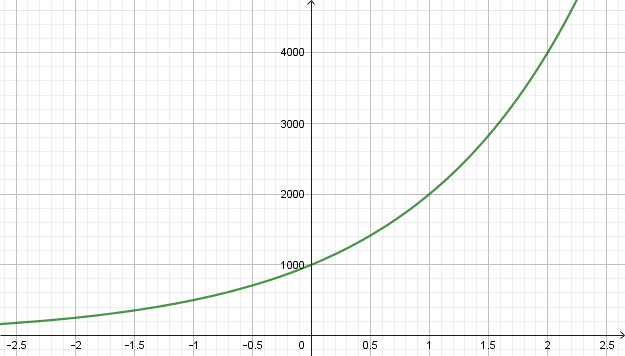
Veremos daqui a pouco algumas propriedades que justifiquem este gráfico. Ele não é obtido simplesmente ``ligando pontos" conhecidos. Apenas ligando pontos, nada nos garantiria que o gráfico
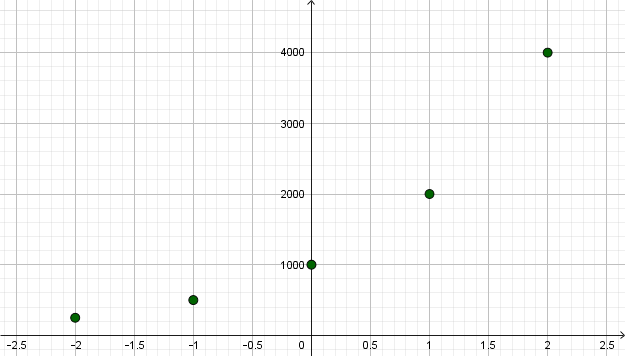
não nos daria algo como
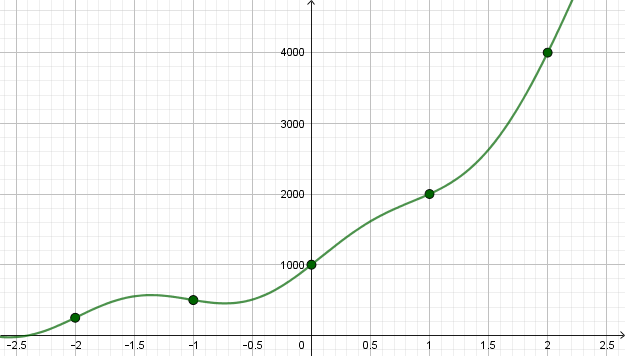
Uma população de bactérias possui, inicialmente, $P_0$ indivíduos. Qual seria a expressão deste número de indivíduos se ele aumentasse 50% a cada hora?
Após o aumento de 50% da primeira hora, teremos
\[{P_0} \underset{1\;\textnormal{hora depois}}{\xrightarrow{\,}} {P_0} + 50\% \cdot \,{P_0} = \frac{100\% \cdot \,P_0}{100} + \frac{50\% \cdot \,P_0}{100} = \frac{150\% \cdot \,P_0}{100} = \frac{3}{2} \cdot \,P_0\]
Assim,
\[P(1) = P_0 \cdot \left(\frac{3}{2}\right)^1.\]Passada mais uma hora, teremos
\[P(2) = P(1) \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^1 \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^2.\]Prosseguindo assim,
\[P(3) = P(2) \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^2 \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^3,\]\[P(4) = P(3) \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^3 \cdot \frac{3}{2} = P_0 \cdot \left(\frac{3}{2}\right)^4,\]
\[\vdots\]
\[P(n) =P_0 \cdot \left(\frac{3}{2}\right)^n, n \in \mathbb{N}\]
Generalizando como fizemos no caso em que a população dobrava,
\[P(t) = P_0\cdot\left(\frac{3}{2}\right)^t, t \in \mathbb{R}.\]De maneira geral, qualquer crescimento a um fator $a > 1$ a cada unidade de tempo nos daria
\[P(t) = P_0 \cdot a^t, t \in \mathbb{R}.\] Nos exemplos anteriores, $a=2$ e $a= \frac{3}{2}$, respectivamente.
Mas também existem fenômenos em que temos a redução de uma grandeza a um mesmo fator a cada unidade de tempo, como no exemplo a seguir.
A cada ano, 20% de uma massa $M_0$ de isótopos radioativos de um certo elemento se converte em isótopos não radioativos.
Após um ano, teremos
\[M_0 \underset{1\;\mathrm{ano}}{\longrightarrow} M_0 - 20\%M_0 = \frac{100\; M_0}{100} - \frac{20\; M_0}{100} = \frac{80\; M_0}{100} = \frac{4}{5}\; M_0\]Assim, como nos exemplos anteriores,
\[M(0) = M_0 = M_0 \cdot \left(\frac{4}{5}\right)^0 \]\[M(1) = M_0 \cdot \frac{4}{5} = M_0 \cdot \left(\frac{4}{5}\right)^1 \]
\[M(2) = \left[M_0 \cdot \frac{4}{5}\right] \cdot \frac{4}{5} = M_0 \cdot \left(\frac{4}{5}\right)^2 \]
\[\vdots\]
\[M(n) = M_0 \cdot \left(\frac{4}{5}\right)^n,\;n \in \mathbb{N}\]
Da mesma forma que foi feito no primeiro exemplo, podemos generalizar esta expressão para todo $t \in \mathbb{R}$, obtendo
\[M(t) = M_0 \cdot \left(\frac{4}{5}\right)^t,\;t \in \mathbb{R}.\]
Uma função $f:\mathbb{R}\rightarrow\mathbb{R}$ será exponencial se sua expressão for da forma
\[f(x)=a^x,\]para algum número real $a > 0$.
Vamos entender um pouco melhor a expressão da função exponencial. A base, $a$, é um número real positivo fixo, o que varia é o expoente $x$. É diferente de uma função potência, com expressão na forma $f(x) = x^n$, em que o expoente é fixo e a base é quem varia.
O gráfico da função exponencial é como um dos gráficos abaixo, dependendo do valor de $a$.

Observe que, quando $a=1$ a função é constante e igual a 1, pois $1^x= 1$ para todo $x \in \mathbb{R}$.
Uma função exponencial $f:\mathbb{R}\rightarrow\mathbb{R}, f(x)=a^x$, com $a > 0$ será sempre positiva, isto é, $f(x) > 0$ para todo $x \in \mathbb{R}$.
Esta proposição é consequência direta da propriedade (iv) de potências, da primeira seção.
Outra observação muito importante é que, para qualquer base $a>0$,
Uma característica importante da função exponencial está na razão entre sua variação e seu valor. Vamos considerar uma função exponencial de expressão $f(x) = a^x$. Agora, fixemos um número positivo $\Delta x$. Para um valor qualquer de $x_0 \in \mathbb{R}$, a variação do valor da função entre $x_0$ e $x_0+\Delta x$ é dada por
\[\Delta f = f(x_0+\Delta x) - f(x_0).\]No exemplo abaixo, vamos calcular a variação de $f(x)= \left(\frac{3}{2}\right)^x$, quando $\Delta x=2$, para dois valores diferentes de $x_0$. Depois, vamos dividir esta variação por $f(x_0)$, para ver o que obtemos.
| $x_0 = 1$ | $x_0 = 2$ | |
| $f(x_0) = f(1) = \left(\frac{3}{2}\right)^1 = 1,\!5$ | $f(x_0) = f(2) = \left(\frac{3}{2}\right)^2 = 2,\!25$ | |
| $f(x_0+2) = f(1+2) = \left(\frac{3}{2}\right)^3 = 3,\!375$ | $f(x_0+2) = f(2+2) = \left(\frac{3}{2}\right)^4 = 5,\!0625$ | |
| $\Delta f = f(x_0+2) - f(x_0) = 1,\!875$ | $\Delta f = f(x_0+2) - f(x_0) = 2,\!8125$ | |
| $\dfrac{\Delta f}{f(x_0)} = \dfrac{1,\!875}{1,\!5} = 1,\!25$ | $\dfrac{\Delta f}{f(x_0)} = \dfrac{3,\!8125}{2,\!25} = 1,\!25$ |
As razões entre $\Delta f$ e $f(x_0)$ calculadas acima ficaram iguais! Isso não é exclusividade deste exemplo. Sempre que fixarmos $\Delta x > 0$, a razão $\dfrac{f(x + \Delta x) - f(x)}{f(x)}$ será constante.
Você pode experimentar um pouco o cálculo desta razão no applet disponível em:
O fato desta razão ser constante não deveria ser uma surpresa. Lembre-se dos exemplos que vimos no começo deste texto. Neles, para cada intervalo de tempo fixado ($\Delta x$), a variação de uma grandeza ($\Delta f = f(x_0 + \Delta x) - f(x_0)$) era proporcional ao valor da mesma grandeza no começo do intervalo ($f(x_0)$).
Vamos verificar que isso realmente sempre ocorre.
Assim,
\[\frac{\Delta f}{f(x_0)} = \frac{f(x_0)(a^{\Delta x} - 1)}{f(x_0)} = \underbrace{(a^{\Delta x} - 1)}_{\mathrm{constante}} \] Logo, concluímos que, fixada a variação $\Delta x$ do parâmetro $x$, a variação $\Delta f$ da função naquele intervalo será proporcional ao valor $f(x_0)$ da função no começo do intervalo.
Podemos ainda tirar outras conclusões a partir da expressão
que obtivemos.
Se \(a > 1\), como \(\Delta x > 0\), teremos \(a^{\Delta x} > 1\), logo \(a^{\Delta x}-1 > 0\). Com isso,
Ou seja, a variação da função é positiva em qualquer intervalo. Portanto a função \(f\) é crescente.
Se \(0 < a < 1\), como \({\Delta x} > 0\), teremos \(a^{\Delta x} < 1\), logo \(a^{\Delta x}-1 < 0\). Com isso,
Ou seja, se $0 < a < 1$, a variação da função é negativa em qualquer intervalo. Portanto a função $f$ é decrescente.
Se \(a=1\), temos \(a^{\Delta x} = 1\), logo \(a^{\Delta x}-1 = 0\). Portanto, a variação de $f$ é sempre nula, o que já era esperado, pois \(f\) é constante. Assim, para deixar registrado o que concluímos, vamos enunciar uma proposição:
Seja $f:\mathbb{R} \rightarrow \mathbb{R}$, dada por $f(x) = a^x$, com $a > 0$.
Se $0 < a < 1$, $f$ é decrescente, isto é, $x_0 < x_1$ se, e somente se, $f(x_0) > f(x_1)$.
Se $a > 1$, $f$ é crescente, isto é, $x_0 < x_1$ se, e somente se, $f(x_0) < f(x_1)$.
Se $a=1$, $f$ é constante e igual a 1, isto é, $f(x) = 1$ para todo $x \in \mathbb{R}$.
Podemos também calcular a variação média da exponencial, isto é, a razão $\frac{\Delta f}{\Delta x}$. Pelo que calculamos acima,
\[\frac{\Delta f}{\Delta x} = \frac{f(x_0)(a^{\Delta x} - 1)}{\Delta x} = f(x_0)\underbrace{\frac{(a^{\Delta x} - 1)}{\Delta x}}_{\begin{array}{c}\textnormal{constante, pois $a$}\\\textnormal{e $\Delta x$ são fixados}\end{array}},\] que também não varia com a mudança do $x_0$. Esta variação média depende apenas do $\Delta x$ e do $a$ fixados.
Uma consequência, da Proposição anterior é que, se a base $a$ for diferente de 0, a função exponencial sempre mudará de valor quando houver mudança do parâmetro $x$. Com isso, podemos também enunciar o resultado a seguir.
A função $f:\mathbb{R} \rightarrow \mathbb{R}$, dada por $f(x) = a^x$, com $a > 0$ e $a \neq 1$ é injetiva, isto é,
se $x_0 \neq x_1$ então $f(x_0) \neq f(x_1)$,
equivalentemente, se $f(x_0) = f(x_1)$ então $x_0 = x_1$.
Vamos comparar duas exponenciais de bases diferentes $a$ e $b$, com $ 0 < a < b$. Considere as funções $f: \mathbb{R} \rightarrow \mathbb{R}$ e $g: \mathbb{R} \rightarrow \mathbb{R}$ dadas por $f(x) = a^x$ e $g(x) = b^x$.
Para $x >0$,
Como $b > a$, temos $\frac{b}{a} > 1$ e, como $x >0$, temos $\left(\frac{b}{a}\right)^x > 1$. Logo
\[\frac{g(x)}{f(x)} > 1.\] Com isso, $g(x) > f(x)$.
Assim, para um mesmo $\boldsymbol{x > 0}$, quanto maior a base, maior o valor da função.
Para $x < 0$,
Como $a < b$, temos $\frac{a}{b} < 1$ e, como $-x >0$, temos $\left(\frac{a}{b}\right)^{-x} < 1$. Logo
\[\frac{g(x)}{f(x)} < 1.\] Com isso, $g(x) < f(x)$.
Assim, para um mesmo $\boldsymbol{x < 0}$, quanto maior a base, menor o valor da função.
O esboço abaixo mostra alguns exemplos de gráficos de funções exponenciais. Tente observar as relações obtidas nos parágrafos anteriores. Note que, para $x0$, quanto maior a base, mais acima está o gráfico da exponencial correspondente. Para $x<0$, a situação se inverte.
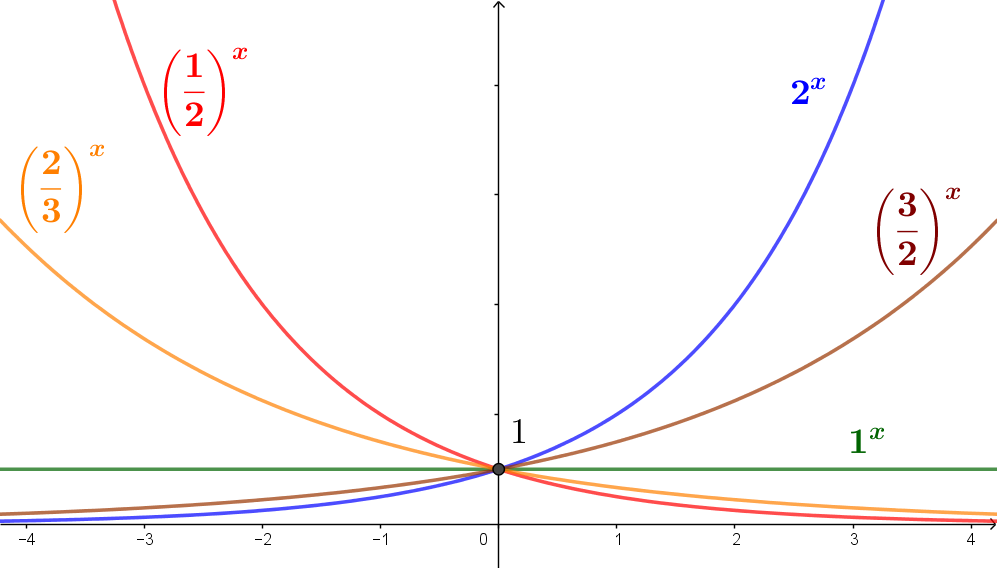
\[\small \frac{1}{2}<\frac{2}{3}<1<\frac{3}{2}<2\]
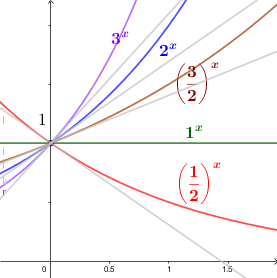
Nas esboço anterior, vamos exibir as retas tangentes (não importa ainda como as obtivemos!) aos gráficos das funções exponenciais exibidas, no ponto $(0,1)$.
Agora vamos olhar com maior aproximação para o gráfico e as tangentes de duas dessas funções, de bases 2 e 3.
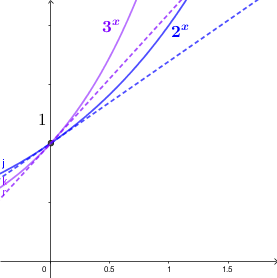
Vamos traçar a reta $x=y$, de coeficiente angular 1, que é a diagonal principal do plano cartesiano. Depois, traçaremos a reta $y=x+1$, paralela a $y=x$ e passando pelo ponto $(0,1)$.
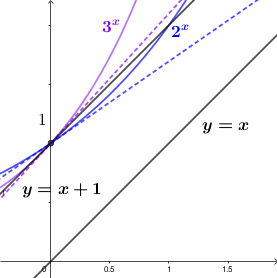
Podemos perceber que a inclinação desta reta está entre as inclinações das retas tangentes a
$f(x)= 2^x$ e $g(x)= 3^x$ em $(0,1)$. É razoável, portanto, acreditar que, para alguma base especial $a$, com $2 < a < 3$, a reta tangente ao gráfico da função $h(x)=a^x$ é dada por $y=x+1$.
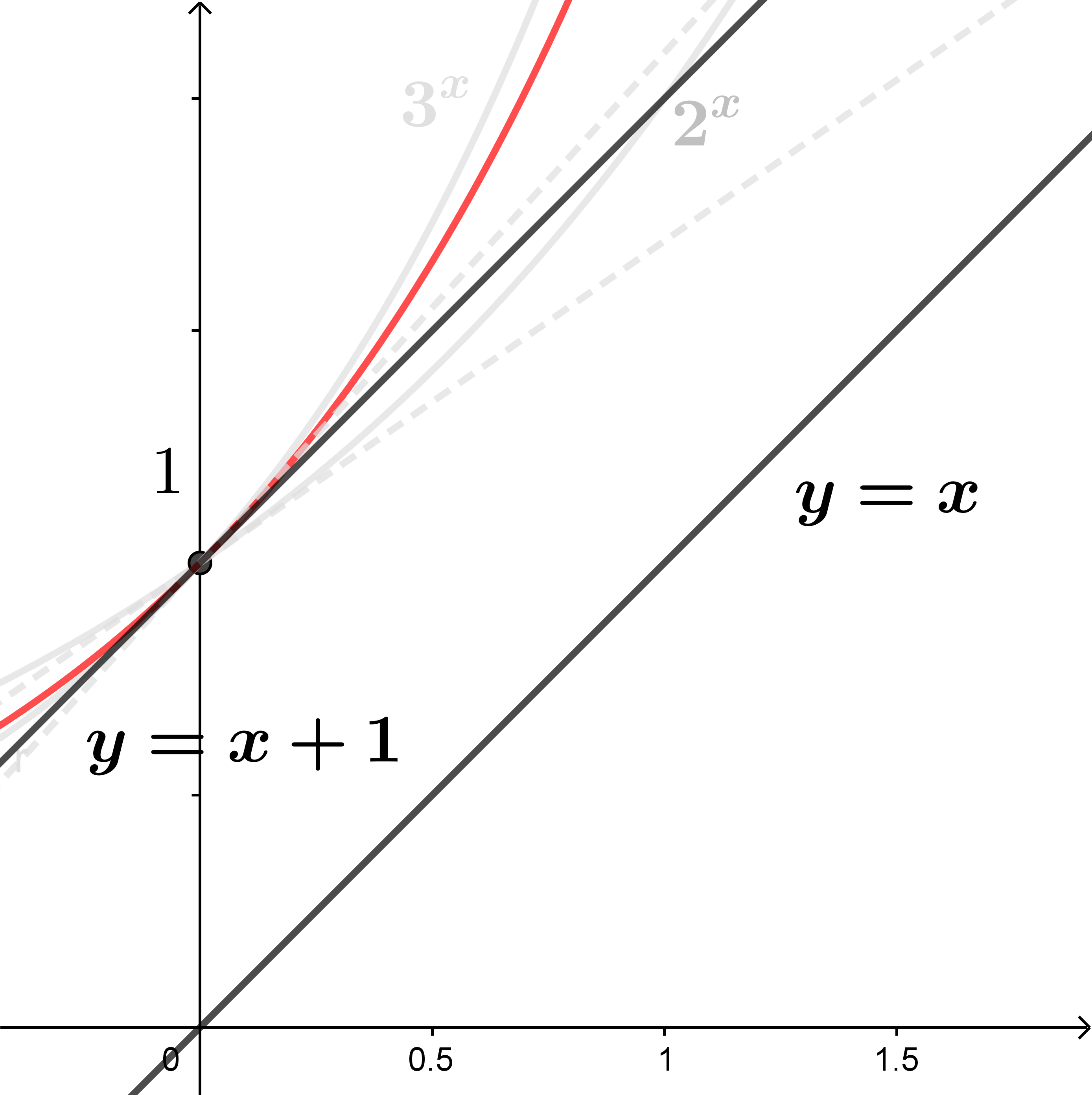
Esta base especial existe, e é dada por um número irracional muito especial, denotado por $e$ e cujos primeiros dígitos são
\[e = 2,\!71828182846...\]
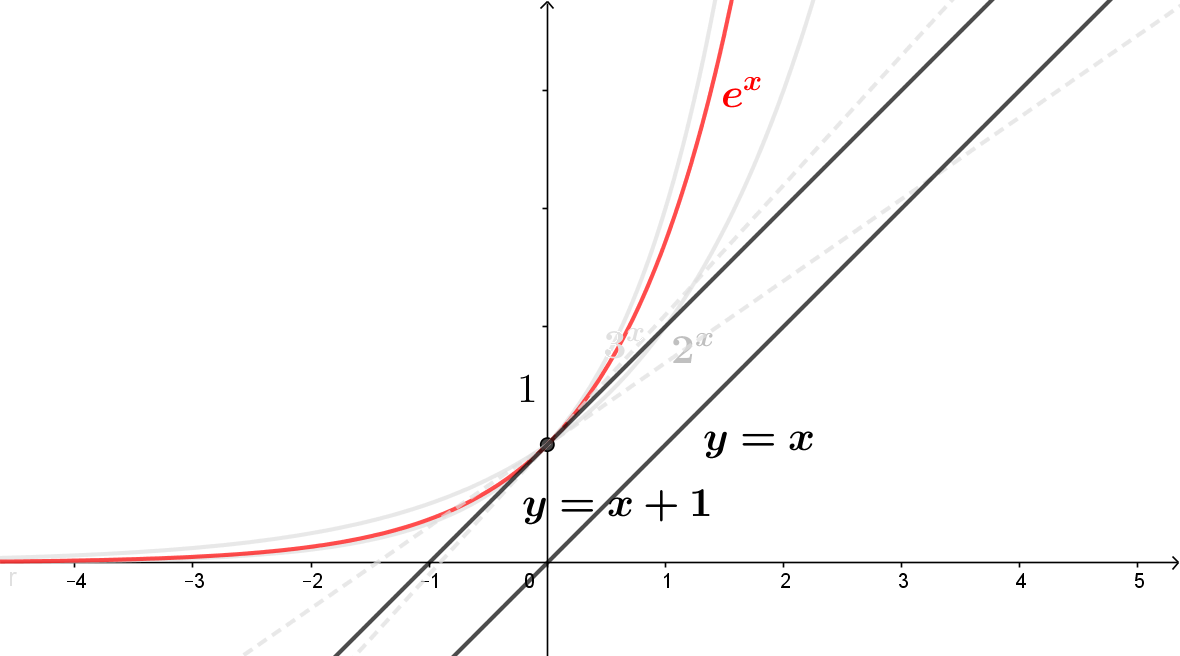
A função exponencial dada por $f(x) = e^x$ é também denotada por $\exp(x)$, de tão especial que é.
O número $e = 2,\!71828182846...$ é chamado, entre outros nomes, de número de Euler, número de Napier, base natural e desempenhará um papel fundamental na disciplina Cálculo 1A. Mas, por enquanto, não se preocupe com ele; o importante agora é apenas saber se sua existência, saber que é algo ali entre $2,\!5$ e 3. Este número pode até parecer meio esquisitão à primeira vista, mas saiba que sua aparição em qualquer problema de Cálculo certamente torna tudo mais fácil! A modelagem da maior parte dos fenômenos naturais atraem (naturalmente!) o número $e$, de tão bonito que ele é.
Guarde bem o que vou dizer, para que eu possa cobrar no futuro. Você ainda ficará muito feliz quando uma exponencial $f(x) = e^x$ cruzar o seu caminho em um problema de derivadas ou integrais!
As Proposições 2 e 3 são muito importantes para resolvermos equações e inequações em que a variável apareça no expoente de expressões.
Resolver, para $x \in \mathbb{R}$, a equação
\[3^x = 27.\]
Lembre-se de que a função exponencial é crescente (se a base for $a > 1$) ou decrescente (se a base for $0 < a < 1$). De qualquer forma, ela é injetiva.
Considerando a função $f(x) = 3^x$, a equação se transforma em
Note que $27 = 3^3 = f(3)$. Assim, a equação se torna
\[f(x) = f(3).\] Como $f$ é injetiva, se $f(x) = f(3)$, temos $x = 3$.
Resolver, para $x \in \mathbb{R}$, a equação
\[2^{x^2} = 2^x.\]Considerando a função $f(x) = 2^x$, que é injetiva,
\[2^{x^2} = 2^x \Leftrightarrow f\left(x^2\right) = f(x) \Leftrightarrow x^2 = x \Leftrightarrow x=0 \textnormal{ ou } x=1.\]
Resolver, para $x \in \mathbb{R}$, a equação
\[2^{x^2} = \left(\frac{1}{2}\right)^x.\]
Considerando a função $f(x) = 2^x$, que é injetiva,
\[2^{x^2} = \left(\frac{1}{2}\right)^x \Leftrightarrow 2^{x^2} = 2^{-x} \Leftrightarrow f\left(x^2\right) = f(-x) \Leftrightarrow x^2 = -x\]\[\Leftrightarrow x=0 \textnormal{ ou } x=-1.\]
Resolver, para $x \in \mathbb{R}$, a inequação
\[3^x > 81.\]
Considerando a função $f(x) = 3^x$, a inequação se transforma em
\[f(x) > f(4).\]Como a base $3$ da função exponencial $f$ é maior que 1, $f$ é crescente, logo
\[3^x > 81 \Leftrightarrow f(x) > f(4) \Leftrightarrow x > 4.\]
Resolver, para $x \in \mathbb{R}$, a inequação
\[\left(\frac{1}{2}\right)^x > 8\]
Considerando a função $f(x) = \left(\frac{1}{2}\right)^x$, a inequação se transforma em
\[f(x) > f(-3),\]pois $\left(\frac{1}{2}\right)^{-3} = 2^3 = 8$. Como a base $\frac{1}{2}$ da função exponencial $f$ é menor que 1, $f$ é decrescente, logo
\[\left(\frac{1}{2}\right)^x > 8 \Leftrightarrow f(x) > f(-3) \Leftrightarrow x < -3.\]Poderíamos também resolver esta inequação de outra forma. Considerando a função $f(x) = 2^x$, a inequação se transforma em
\[f(-x) > f(3),\]pois $2^{-x} = \left(\frac{1}{2}\right)^x$ e $2^3 = 8$. Como a base 2 da função exponencial $f$ é maior que 1, $f$ é crescente, logo
\[\left(\frac{1}{2}\right)^x > 8 \Leftrightarrow f(-x) > f(3) \Leftrightarrow -x > 3 \Leftrightarrow x < -3.\]
Resolver, para $x \in \mathbb{R}$, a equação
\[4^x - 3\cdot 2^x = 4.\]
Note que $4^x = (2^2)^x = (2^x)^2$. Fazendo $y=2^x$,
\[4^x - 3\cdot 2^x = 4 \Leftrightarrow y^2 - 3y = 4 \Leftrightarrow y^2 - 3y - 4 = 0 \Leftrightarrow \]\[ \Leftrightarrow y = 4 \textnormal{ ou } y = -1.\]
Assim, a solução da equação é dada pelos $x\in\mathbb{R}$ tais que
\[2^x = 4 \textnormal{ ou } 2^x = -1.\]Como não existe $x\in\mathbb{R}$ tal que $2^x = -1$ (por quê?),
\[4^x - 3\cdot 2^x = 4 \Leftrightarrow 2^x = 4 \textnormal{ ou } 2^x = -1 \Leftrightarrow x = 2.\]
Resolver, para $x \in \mathbb{R}$, a inequação
\[4^x - 3\cdot 2^x > 4.\]
Fazendo $y=2^x$,
\[4^x - 3\cdot 2^x > 4 \Leftrightarrow y^2 - 3y - 4 > 0 \Leftrightarrow y > 4 \textnormal{ ou } y < -1.\]Assim, a solução da equação é dada pelos $x\in\mathbb{R}$ tais que
\[2^x > 4 \textnormal{ ou } 2^x < -1.\]Como não existe $x\in\mathbb{R}$ tal que $2^x < -1$ (por quê?),
\[4^x - 3\cdot 2^x > 4 \Leftrightarrow 2^x > 4 \textnormal{ ou } 2^x < -1 \Leftrightarrow 2^x > 2^2 \Leftrightarrow x > 2.\]