
Você consegue se lembrar das razões trigonométricas no triângulo retângulo?

\[\mathrm{sen}(\widehat{B}) = {\displaystyle \frac{\text{cateto oposto}}{\text{hipotenusa}}} {= \displaystyle \frac{b}{a},} \qquad \cos(\widehat{B}) = {\displaystyle \frac{\text{cateto adjacente}}{\text{hipotenusa}}} {= \displaystyle \frac{c}{a},} \qquad \mathrm{tg}(\widehat{B}) = {\displaystyle \frac{\text{cateto oposto}}{\text{cateto adjacente}}} {= \displaystyle \frac{b}{c}.}\]
Estas razões estão definidas para um ângulo $B$ de medida $0^\circ <\hat{B} < 90^\circ$.
Há três ângulos cujas razões trigonométricas são muito especiais, $30^\circ$, $45^\circ$ e $60^\circ$.

Considerando o quadrado de lado $b$ da figura à esquerda e traçando sua diagonal $BC$, temos $c=b$ e $a=\sqrt{2}\,B$. Assim,
\[\mathrm{sen}(45^\circ) = \frac{b}{a} = \frac{b}{\sqrt{2}\,b} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}.\]\[\cos(45^\circ) = \frac{c}{a} = \frac{b}{\sqrt{2}\,b} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}.\]
\[\mathrm{tg}(45^\circ) = \frac{b}{c} = \frac{b}{b} = 1.\]

Considerando o triângulo equilátero $BDC$ de lado $a$ da figura à esquerda, traçando sua altura $AC$, temos $c=\frac{a}{2}$ e $b=\frac{a\sqrt{3}}{2}$. Assim, olhando para o ângulo $\hat{B} = 60^\circ$,
\[\mathrm{sen}(60^\circ) = \frac{b}{a} = \frac{\frac{a\sqrt{3}}{2}}{a} = \frac{\sqrt{3}}{2}.\]\[\cos(60^\circ) = \frac{c}{a} = \frac{\frac{a}{2}}{a} = \frac{1}{2}.\]
\[\mathrm{tg}(60^\circ) = \frac{b}{c} = \frac{\frac{a\sqrt{3}}{2}}{\frac{a}{2}} = \sqrt{3}.\]
Olhando agora para o ângulo $\hat{C} = 30^\circ$,
\[\mathrm{sen}(30^\circ) = \frac{c}{a} = \frac{\frac{a}{2}}{a} = \frac{1}{2}.\]\[\cos(30^\circ) = \frac{b}{a} = \frac{\frac{a\sqrt{3}}{2}}{a} = \frac{\sqrt{3}}{2}.\]
\[\mathrm{tg}(30^\circ) = \frac{c}{b} = \frac{\frac{a}{2}}{\frac{a\sqrt{3}}{2}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}.\]
Hoje, você verá que estas razões trigonométricas podem ser estendidas à funções de domínio $\mathbb{R}$. Para isso, precisaremos sair de um triângulo retângulo, onde os ângulos são limitados ao domínio $(0^\circ, 90^\circ)$.
Também deixaremos de trabalhar com os ângulos medidos em graus e adotaremos uma forma mais natural de expressar ângulos, que, na verdade, passarão a ser arcos.
Você poderá experimentar os conceitos desta seção e da próxima no applet abaixo:
Vamos inciar considerando o círculo de centro em $(0,0)$ e raio 1, da figura abaixo. Considere também o ponto $A=(1,0)$.
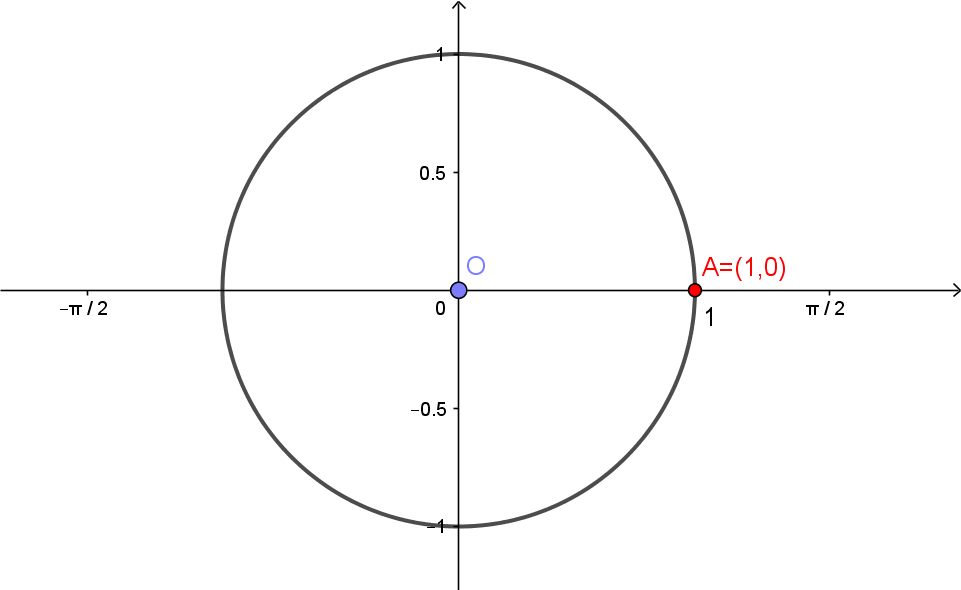
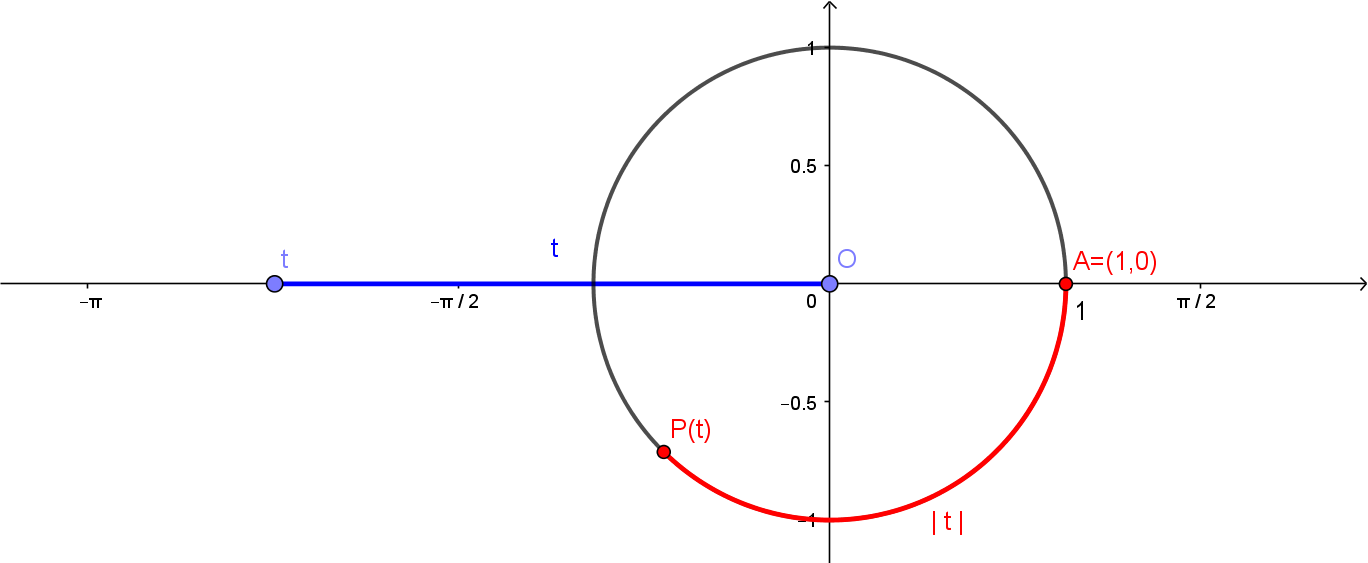
Escolha agora um número real $t > 0$. O comprimento do segmento de extremos $(0,0)$ e $(t,0)$, esboçado abaixo em azul, é $t$. Considere, sobre o círculo, o arco de comprimento $t$, desenhado a partir de $A$ e percorrendo o círculo no sentido anti-horário, como na figura abaixo. Chame de $P(t)$ o outro extremo deste arco.
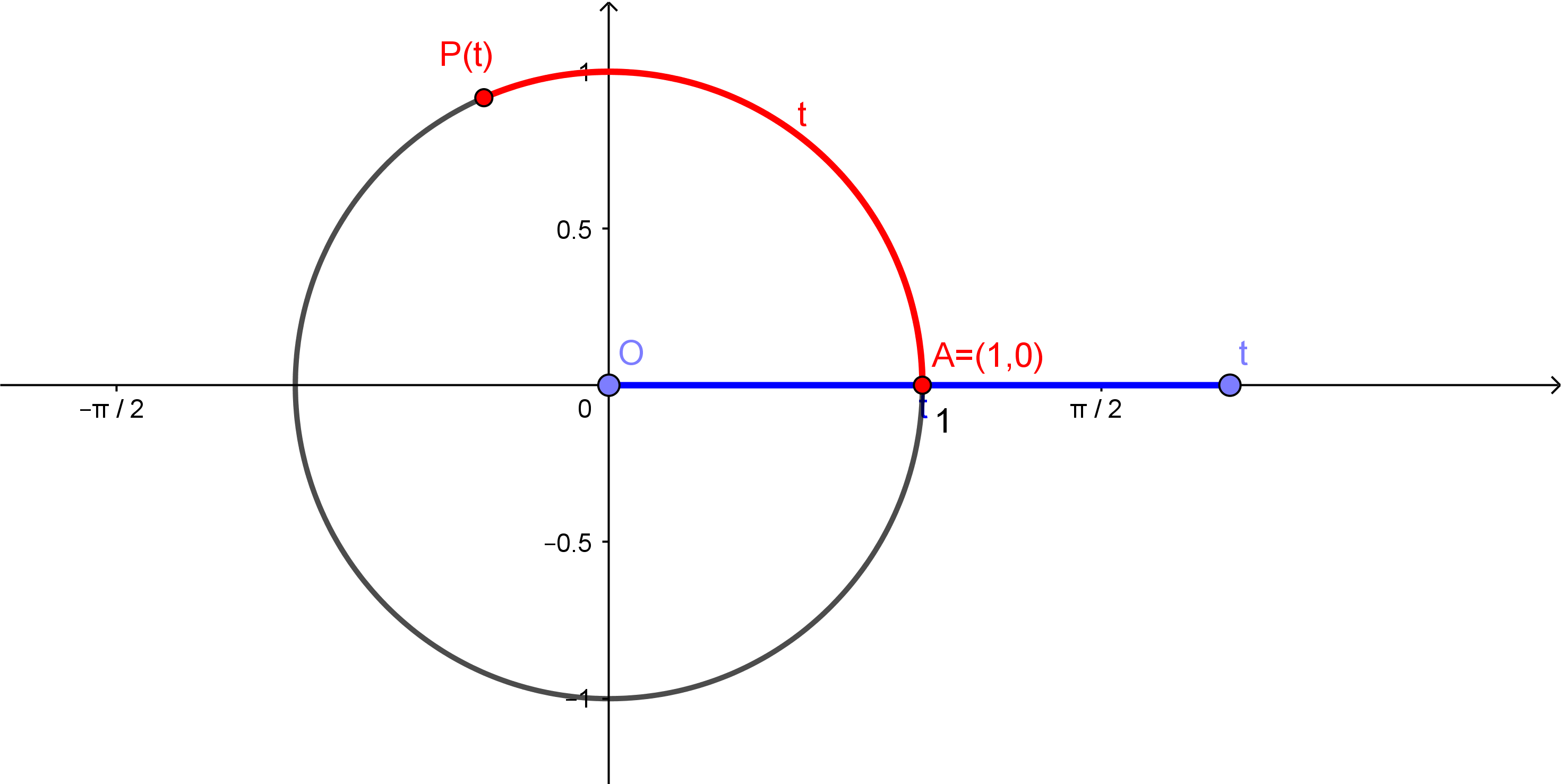
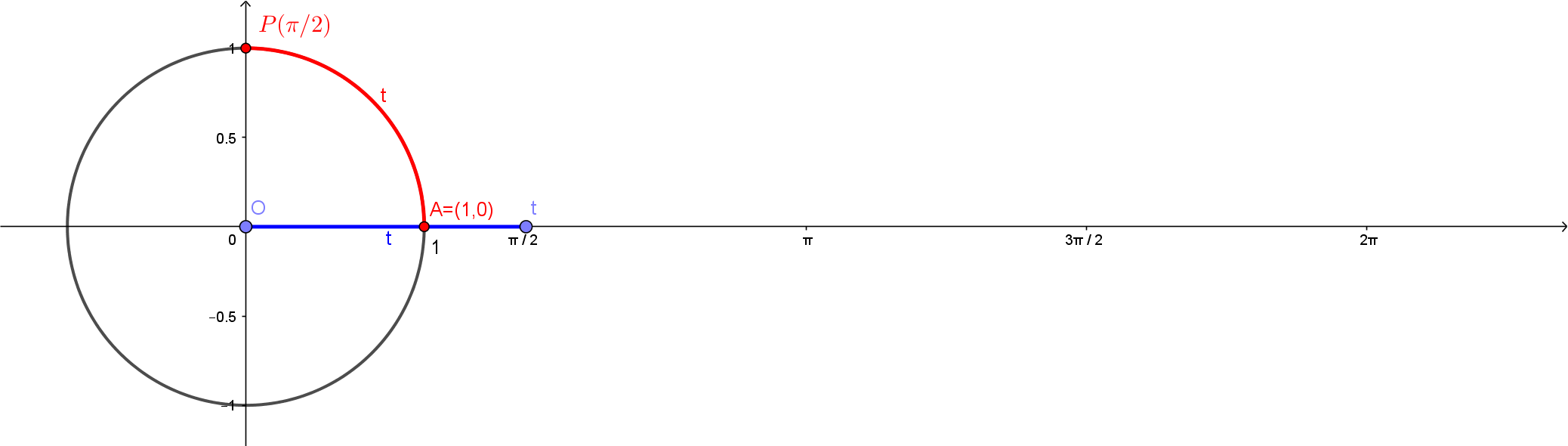
Uma observação importante é que como o raio deste círculo é $r=1$, o comprimento deste círculo inteiro será dado por $2\pi \cdot r = 2\pi$. Com isso, temos nas figuras abaixo os pontos $P(\pi/2)$, $P(\pi)$, $P(3\pi/2)$ e $P(2\pi)$.
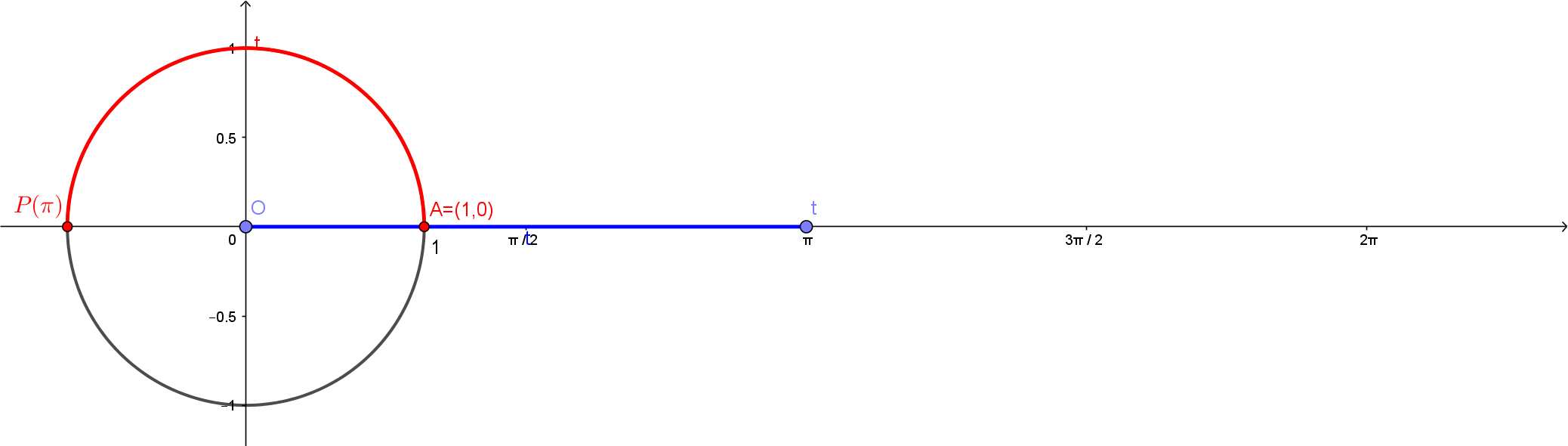


Também podemos ter $t<0$. Neste caso, será percorrido um arco de comprimento $|t|$, também a partir de $A = (1,0)$, porém no sentido horário.
Na figura abaixo, destacamos alguns pontos interessantes.
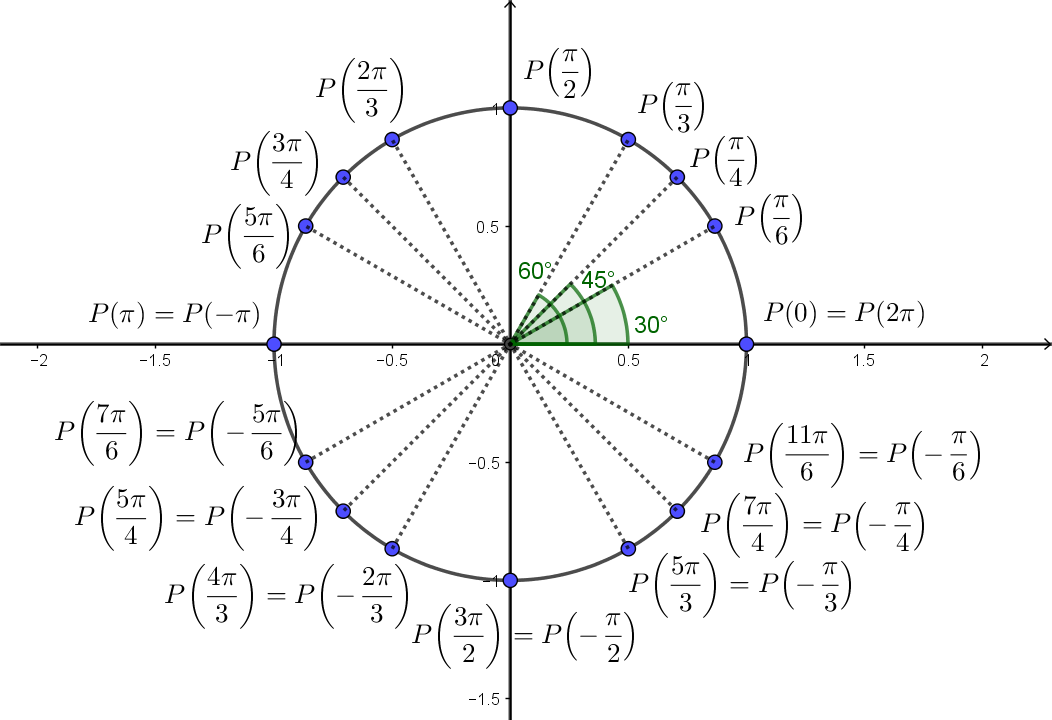
Para marcar alguns destes pontos, lembre $2\pi$ corresponde ao círculo inteiro, logo $\pi$ corresponde a meio círculo, $\pi/2$ a um quarto, $\pi/3$ a um sexto e $\pi/6$ a um doze-avos.
Alguns pontos foram escritos como correspondentes a mais de um valor de $t$. Na verdade, todos poderiam ter sido escritos assim. Podemos chegar a qualquer ponto do círculo partindo de $A=(1,0)$ e percorrendo o círculo no sentido horário ou anti-horário. Na verdade, cada ponto pode ser atingido percorrendo o círculo com infinitos arcos diferentes, basta ficarmos dando muitas voltas.
Cada volta completa no círculo, seja no sentido horário ou anti-horário, nos levará ao mesmo ponto de partida. Assim, todos os arcos de comprimento $2k\pi$, com $k$ inteiro, percorridos a partir de $A$ nos levam... de volta ao próprio ponto $A$. Assim, para todo $k \in \mathbb{Z}$,
De maneira geral, se a diferença entre o comprimento de dois arcos é um número inteiro de voltas, isto é, se eles têm comprimentos $t$ e $t + 2k\pi$, com $k\in\mathbb{Z}$, os arcos terminarão no mesmo lugar, isto é,
\[P(t + 2k\pi) = P(t).\]
Você poderá experimentar os conceitos desta seção e da anterior no applet abaixo:
Considerando o número real $t$ e o ponto $P(t)$ correspondente a ele, como vimos na seção anterior, definimos o cosseno e seno de $t$ respectivamente por
\[\cos(t) = \text{coordenada } x \text{ do ponto } P(t), \]\[\mathrm{sen}(t) = \text{coordenada } y \text{ do ponto } P(t). \]
Isto é, $\mathrm{sen}(t)$ e $\cos(t)$ são tais que
\[P(t) = \left(\cos(t), \mathrm{sen}(t) \right).\]
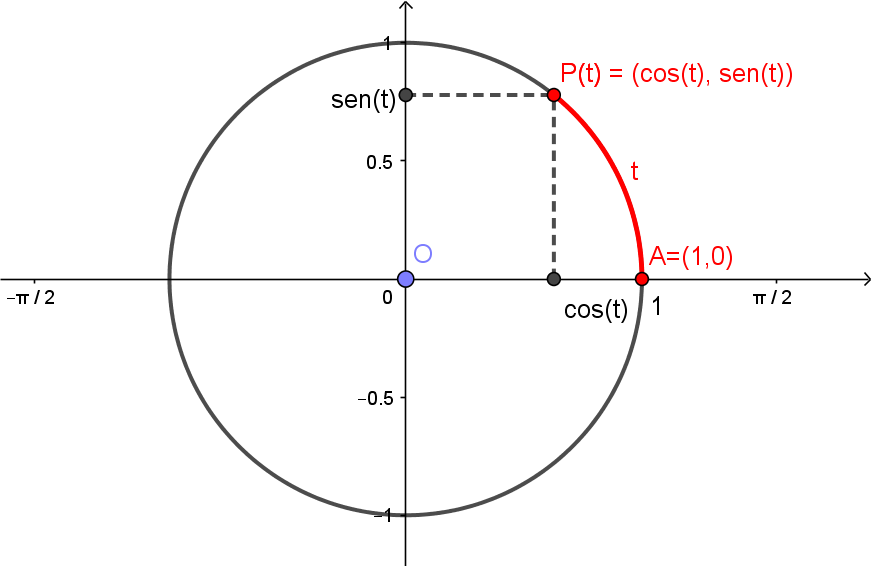
Como as coordenadas de $P(t)$ são $x=\cos(t)$ e $y=\mathrm{sen}(t)$, e como sabemos que este círculo é o conjunto dos pontos $(x,y)$ satisfazendo $x^2+y^2=1$, teremos então
\[\left(\cos(t)\right)^2 + \left(\mathrm{sen}(t)\right)^2 = 1\]ou, como é mais comum escrever
\[\cos^2(t) + \mathrm{sen}^2(t) = 1,\] que é chamada de relação trigonométrica fundamental.
Podemos também observar que, como o raio do círculo é 1,
\[-1 \leqslant \mathrm{sen}(t) \leqslant 1.\]
Observando os pontos do primeiro quadrante, e os ângulos centrais de $30^\circ$, $40^\circ$, e $60^\circ$ que formam, vemos que
\[\begin{array}{ccc} \displaystyle\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}, &\qquad& \displaystyle\mathrm{sen}\left(\frac{\pi}{6}\right) = \frac{1}{2},\\ \\ \displaystyle\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}, &\qquad& \displaystyle\mathrm{sen}\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2},\\ \\ \displaystyle\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}, &\qquad& \displaystyle\mathrm{sen}\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}. \end{array}\]Observando agora os pontos $P(0)$, $P(\pi/2)$, $P(\pi)$ e $P(3\pi/2)$, temos
\[\begin{array}{ccc} \displaystyle\cos\left(0\right) = 1, &\qquad& \displaystyle\mathrm{sen}\left(0\right) = 0,\\ \\ \displaystyle\cos\left(\frac{\pi}{2}\right) = 0, &\qquad& \displaystyle\mathrm{sen}\left(\frac{\pi}{2}\right) = 1,\\ \\ \displaystyle\cos\left(\pi\right) = -1, &\qquad& \displaystyle\mathrm{sen}\left(\pi\right) = 0,\\ \\ \displaystyle\cos\left(\frac{3\pi}{2}\right) = 0, &\qquad& \displaystyle\mathrm{sen}\left(\frac{3\pi}{2}\right) = -1. \end{array}\]Já vimos que $P(t) = P(t+2\pi)$, logo
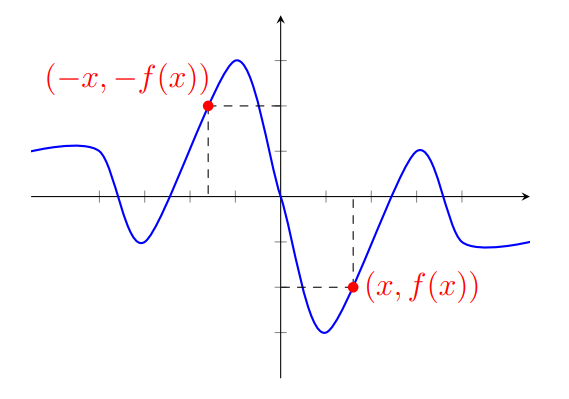
\[\cos(t+2\pi) = \cos(t), ~~\mathrm{sen}(t+2\pi) = \mathrm{sen}(t).\]Na figura abaixo, você pode ver que os pontos $P(t)$ e $P(-t)$ são simétricos em relação ao eixo $x$, pois são atingidos percorrendo arcos de mesmo tamanho, porém em direções opostas.
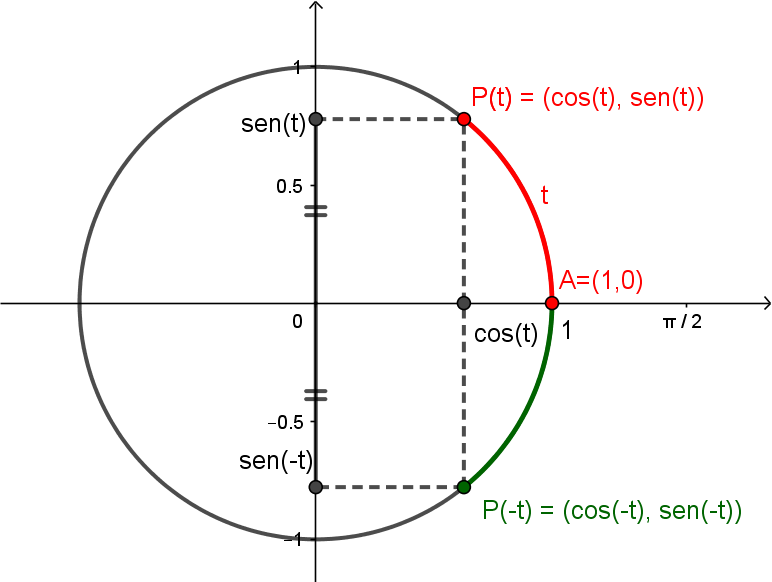
As coordenadas $x$ destes pontos serão as mesmas, logo
\[\cos(-t) = \cos(t).\]As coordenadas $y$ destes pontos serão simétricas, logo
\[\mathrm{sen}(-t) = -\mathrm{sen}(t).\]A diferença entre os arcos correspondentes a $t$ e $t+\pi$ é de $\pi$, que corresponde a meia volta no círculo. Portanto, os pontos $P(t)$ e $P(t+\pi)$ são simétricos, como podemos ver na figura abaixo.
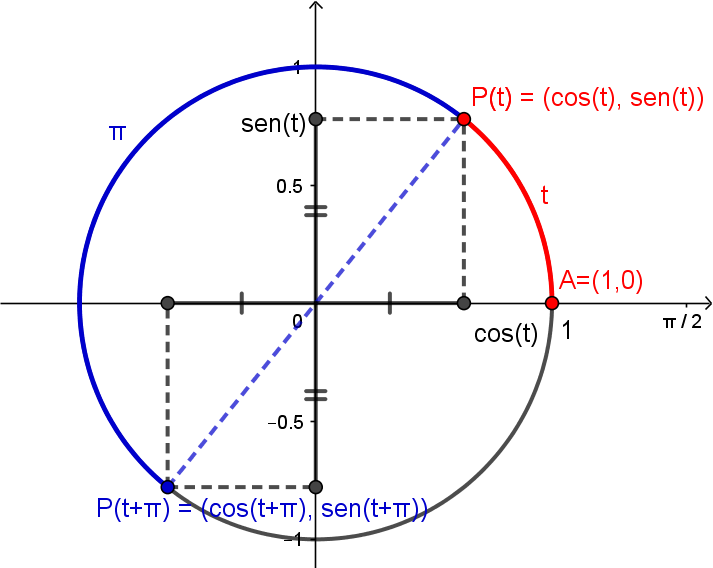
Logo,
\[\cos(t+\pi) = -\cos(t),\]\[\mathrm{sen}(t+\pi) = -\mathrm{sen}(t).\]
Duas relações muito importante, mas que não demonstraremos aqui, são as que nos dão seno e cosseno da soma de dois arcos:
\[\mathrm{sen}(a+b) = \mathrm{sen}(a)\cos(b) + \mathrm{sen}(b)\cos(a),\]\[\cos(a+b) = \cos(a)\cos(b) - \mathrm{sen}(b)\mathrm{sen}(a).\]
Há pessoas que gostam também de "decorar" outras duas relações, para a diferença entre dois arcos. Mas nós não precisamos, pois elas seguem como consequência do que já vimos:
\[\begin{array}{rcll} \mathrm{sen}(a-b) &=& \mathrm{sen}(a + (-b) )\\ \\ &=& \mathrm{sen}(a)\cos(-b) + \mathrm{sen}(-b)\cos(a),& \text{utilizando a fórmula da soma do seno}\\ \\ &=& \mathrm{sen}(a)\cos(b) - \mathrm{sen}(b)\cos(a),& \text{pois $\cos(-t)=\cos(t)$ e $\mathrm{sen}(-t)=-\mathrm{sen}(t)$}\\ \end{array} \]\[\begin{array}{rcll} \cos(a-b) &=& \cos(a + (-b) )\\ \\ &=& \cos(a)\cos(-b) - \mathrm{sen}(-b)\mathrm{sen}(a),& \text{utilizando a fórmula da soma do seno}\\ \\ &=& \cos(a)\cos(b) + \mathrm{sen}(b)\mathrm{sen}(a),& \text{pois $\cos(-t)=\cos(t)$ e $\mathrm{sen}(-t)=-\mathrm{sen}(t)$}\\ \end{array} \]
Na verdade, as pessoas gostam muito de "decorar fórmulas", o que é bem estranho...
Seguindo aplicando as relações da soma de arcos para $a=b=x$, temos ainda que
\[\cos(2x) = \cos(x+x) = \cos(x)\cos(x) - \mathrm{sen}(x)\mathrm{sen}(x) = \cos^2(x)-\mathrm{sen}^2(x).\]
Outra relação muito importante, também decorrente da relação da soma do seno, é que
\[\mathrm{sen}\left(x + \frac{\pi}{2}\right)= \mathrm{sen}(x)\cos\left(\frac{\pi}{2}\right) + \cos(x)\mathrm{sen}\left(\frac{\pi}{2}\right) = \mathrm{sen}(x)\cdot 0 + \cos(x)\cdot 1 = \cos(x),\]ou seja,
\[\cos(x) = \mathrm{sen}\left(x + \frac{\pi}{2}\right).\]Portanto, o cosseno de $x$ tem exatamente o mesmo valor que o seno assumirá em um arco $\pi/2$ maior que $x$.
Calcule $\displaystyle \cos\left(\frac{5\pi}{12}\right)$.
\[\frac{\pi}{4}+\frac{\pi}{6} = \frac{2\pi + 3\pi}{12} = \frac{5\pi}{12},\]
logo
\begin{eqnarray*} \cos\left(\frac{5\pi}{12}\right) &=& \cos\left(\frac{\pi}{4} + \frac{\pi}{6}\right)\\ \\ &=& \cos\left(\frac{\pi}{4}\right)\;\cos\left(\frac{\pi}{6}\right) - \mathrm{sen}\left(\frac{\pi}{4}\right)\;\mathrm{sen}\left(\frac{\pi}{6}\right)\\ \\ &=& \frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2}\cdot\frac{1}{2}\\ \\ &=& \frac{\sqrt{6}}{4} - \frac{\sqrt{2}}{4}\\ \\ &=& \frac{\sqrt{6} - \sqrt{2}}{4} \end{eqnarray*}A chave neste exemplo é perceber que $\frac{5\pi}{12} = \frac{\pi}{4}+\frac{\pi}{6}$. Mas como perceber isso? Pode ajudar se você pensar em graus:
\[\frac{5\pi}{12} \textnormal{ corresponde a } \frac{5}{12}\cdot 180^\circ = 5\cdot 15^\circ = 75^\circ = 45^\circ + 30^\circ, \textnormal{ que corresponde a } \frac{\pi}{4} + \frac{\pi}{6}.\]
Para cada $x \in \mathbb{R}$, definimos na seção anterior $\mathrm{sen}(x)$ e $\cos(x)$. Assim, temos duas funções $\mathrm{sen}: \mathbb{R}\rightarrow \mathbb{R}$ e $\cos: \mathbb{R}\rightarrow \mathbb{R}$, com algumas propriedades que já deduzimos na sessão anterior.
As funções $\mathrm{sen}: \mathbb{R}\rightarrow \mathbb{R}$ e $\cos: \mathbb{R}\rightarrow \mathbb{R}$ satisfazem às seguintes propriedades
$\cos(x) = \cos(-x)$, ou seja, o cosseno é uma função par.
$\mathrm{sen}(-x) = -\mathrm{sen}(x)$, ou seja, o seno é uma função ímpar.
$\cos(x + 2\pi) = \cos(x)$ e $\mathrm{sen}(x+2\pi) = \mathrm{sen}(x)$, ou seja, cosseno e seno são funções periódicas, com período $2\pi$.
$-1 \leqslant \cos(t) \leqslant 1$ e $-1 \leqslant \mathrm{sen}(t) \leqslant 1$.
$\cos(x) = \mathrm{sen}\left(x + \frac{\pi}{2}\right)$
O gráfico de $\mathrm{sen}$ é o conjunto dos pontos da forma $(x,\mathrm{sen}(x))$. Podemos construir este gráfico a partir da definição do seno. Para $x\in\mathbb{R}$, consideramos o ponto $P(x)$ correspondente no círculo, que terá coordenadas $(\cos(x), \mathrm{sen}(x))$. O ponto $(x,\mathrm{sen}(x))$ do gráfico, possui, portanto a mesma coordenada $y$ que $P(x)$, estando portanto na mesma reta horizontal. Mas este ponto $(x,\mathrm{sen}(x))$ também está na mesma reta vertical que $(x,0)$, logo, é a interseção das retas que passam por $P(x)$ e $(x,0)$.
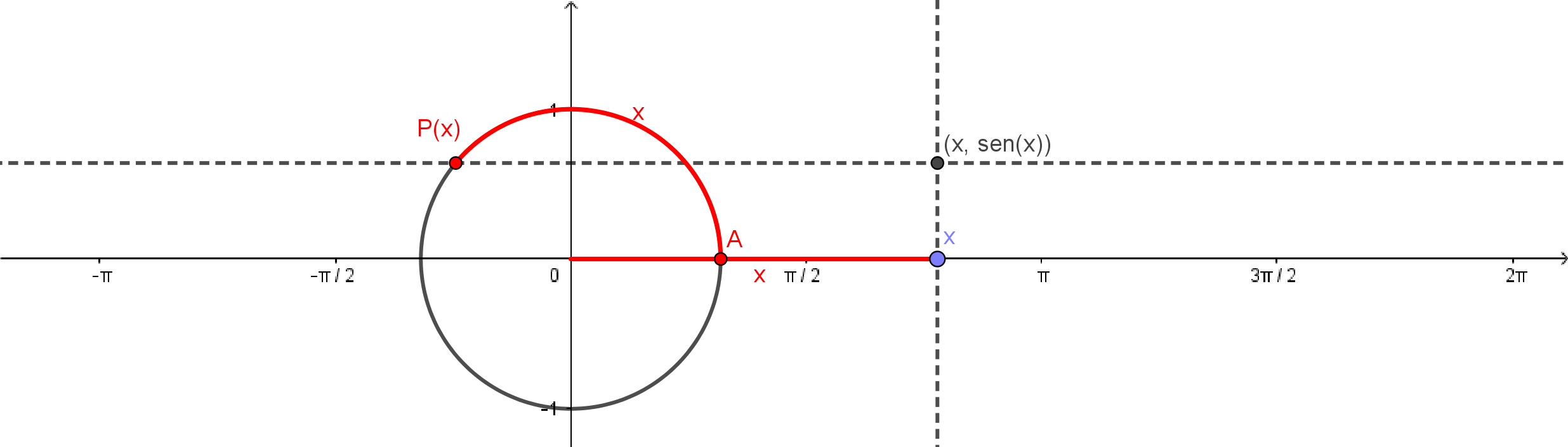
Você pode experimentar uma construção do gráfico, como acima, no applet abaixo:
Abaixo, temos o gráfico do seno construído desta forma:
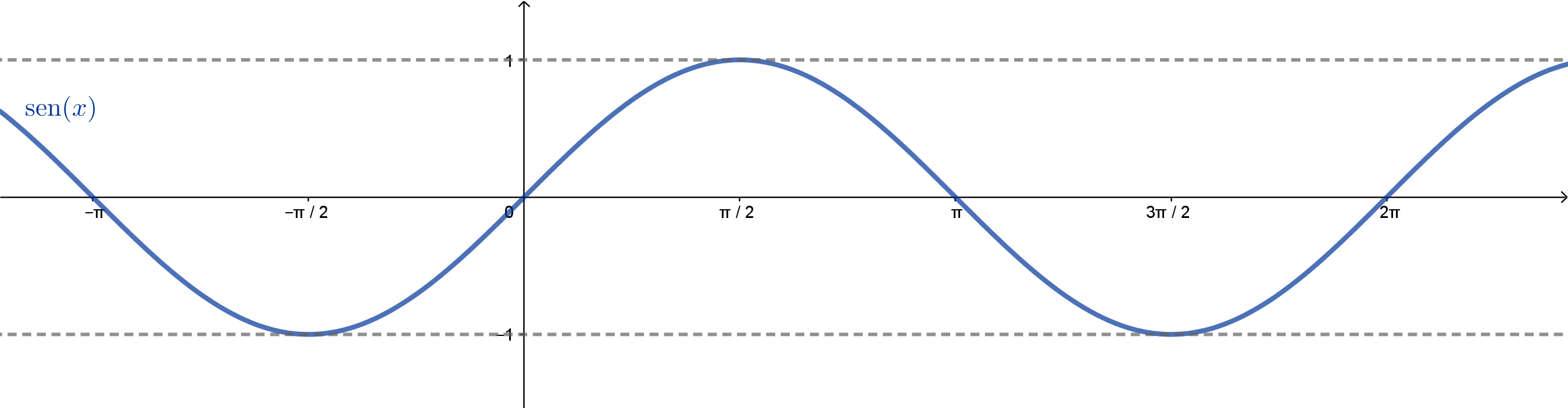
Observe que os valores máximo e mínimo são 1 e $-1$ e que as raízes são os pontos da forma $k\pi$, com $k\in\mathbb{Z}$. Já vimos que o cosseno de $x$ tem exatamente o mesmo valor que o seno assumirá em um arco $\pi/2$ maior que $x$. Por exemplo, teremos $\cos(0) = \mathrm{sen}(\pi/2)$, $\cos(\pi/2) = \mathrm{sen}(\pi)$, etc. Se estivéssemos falando do estudo de um fenômeno, no qual $x$ é o tempo, poderíamos dizer que o cosseno "acontece" $\pi/2$ segundos antes do seno. Com isso, seu gráfico é o mesmo do seno, apenas "antecipado" de $\pi/2$ unidades em $x$.
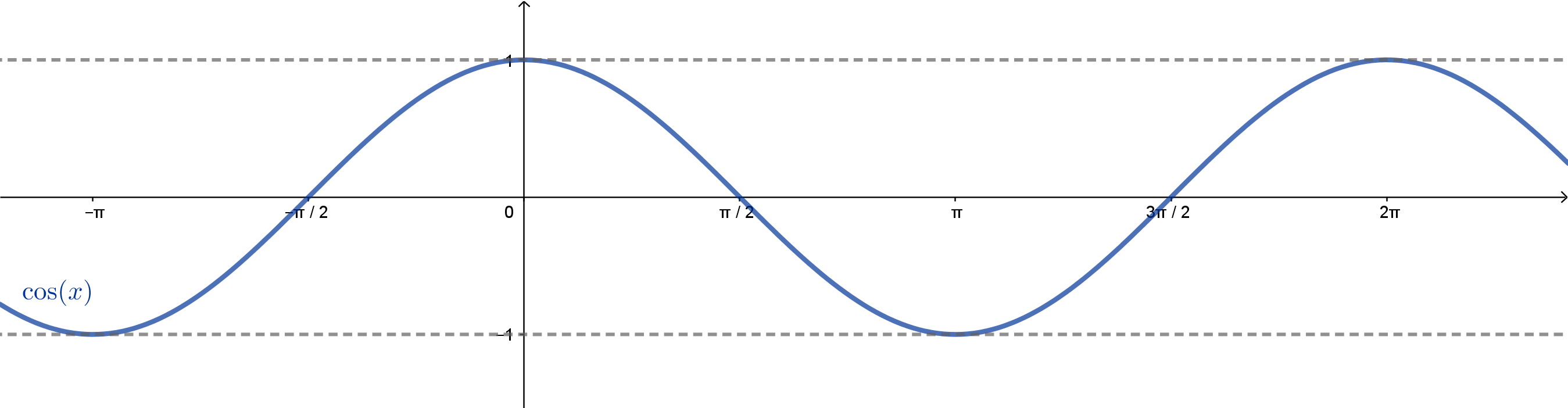
Na próxima seção, veremos que o gráfico do cosseno é obtido por uma translação no gráfico do seno.
Determine os valores de $x \in \mathbb{R}$ para os quais
\[\cos(x) = \frac{1}{2}.\]
Há apenas dois pontos no círculo cuja coordenada horizontal (o cosseno) é igual a $\frac{1}{2}$. O primeiro destes pontos é o correspondente ao arco de $\frac{\pi}{3}$ (que corresponde ao ângulo central de $60^\circ$). O outro ponto, com a mesma coordenada horizontal, é o simétrico ao primeiro com relação ao eixo $x$. Este ponto é o correspondente ao arco de $-\frac{\pi}{3}$.

Assim, a equação é satisfeita por $x=\frac{\pi}{3}$ e por $x=-\frac{\pi}{3}$, mas estes não são os únicos valores de $x$ que tornam válida a igualdade. Qualquer outro valor $x=\frac{\pi}{3}+2k\pi$ ou $x=-\frac{\pi}{3}+2k\pi$, com $k\in\mathbb{Z}$, corresponderá a um dos dois pontos do círculo acima, logo também terão cosseno igual a $\frac{1}{2}$.
Assim,
Determine os valores de $x \in \mathbb{R}$ para os quais
\[\mathrm{sen}(x) \geqslant \frac{\sqrt{2}}{2}.\]
Há apenas dois pontos no círculo cuja coordenada vertical (o seno) é igual a $\frac{\sqrt{2}}{2}$. Estes pontos são os correspondentes aos arcos de $\frac{\pi}{4}$ e o $\frac{3\pi}{4}$.
Como o seno é dado pela coordenada vertical de um ponto do círculo, os pontos cujo seno é maior ou igual a $\frac{\sqrt{2}}{2}$ são aqueles acima da reta $y=\frac{\sqrt{2}}{2}$ ou na reta. O conjunto destes pontos estão representados na figura abaixo:
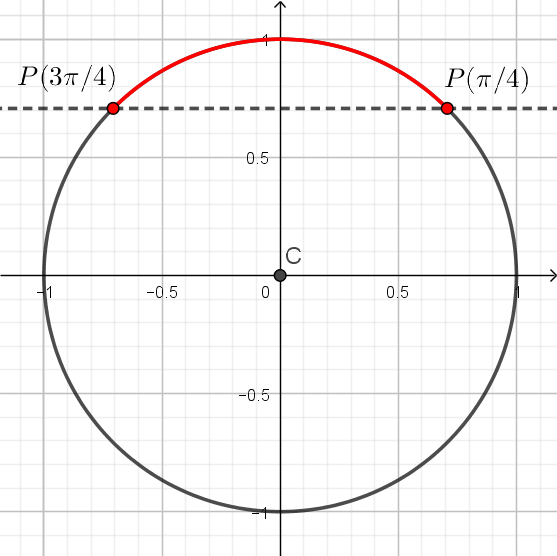
Estes pontos correspondem aos arcos de comprimento $\frac{\pi}{4} \leqslant x \leqslant \frac{3\pi}{4}$. Assim,
\[\mathrm{sen}(x) \geqslant \frac{\sqrt{2}}{2} \text{ para todo } x \in \left[\frac{\pi}{4}, \frac{3\pi}{4}\right].\]Porém, estes não são os únicos arcos que satisfazem a desigualdade. Qualquer arco de comprimento $x$ com $\frac{\pi}{4} + 2k\pi \leqslant x \leqslant \frac{3\pi}{4} + 2k\pi$, com $k \in \mathbb{Z}$, também corresponderá a um dos pontos destacados na figura (serão dadas $k$ voltas e depois percorrido um arco que terá extremo no conjunto destacado). Assim,
\[\mathrm{sen}(x) \geqslant \frac{\sqrt{2}}{2} \text{ para todo } x \in \left[\frac{\pi}{4} + 2k\pi, \frac{3\pi}{4} + 2k\pi\right], \text{ com }k \in \mathbb{Z}.\]
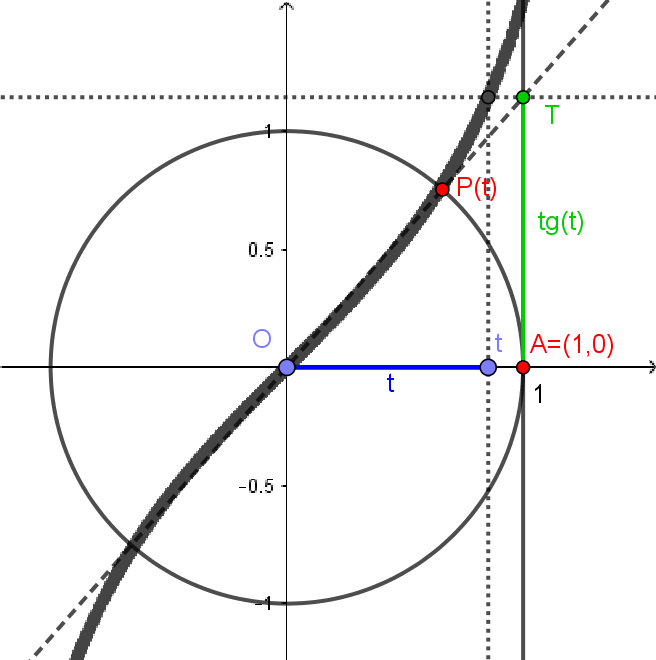
Agora, vamos considerar a reta $r: x=1$, tangente ao círculo. Dado $t \in \mathbb{R}$, tomamos o ponto $P(t)$, como antes. A reta que passa por $(0,0)$ e $P(t)$ cortará a tangente $r$ em um ponto $T$. Definiremos a tangente de $t$, representada por $\mathrm{tg}(t)$, como sendo a coordenada $y$ do ponto $T$. Veja abaixo.
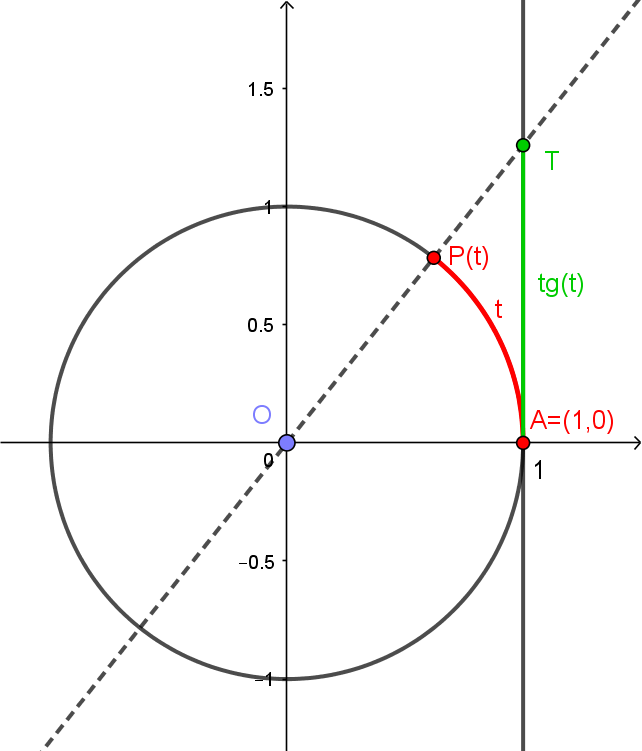
Você pode experimentar uma construção da tangente e seu gráfico no applet abaixo:
Pela semelhança entre os triângulos retângulos $OBP(t)$ e $OAT$ da figura abaixo, temos
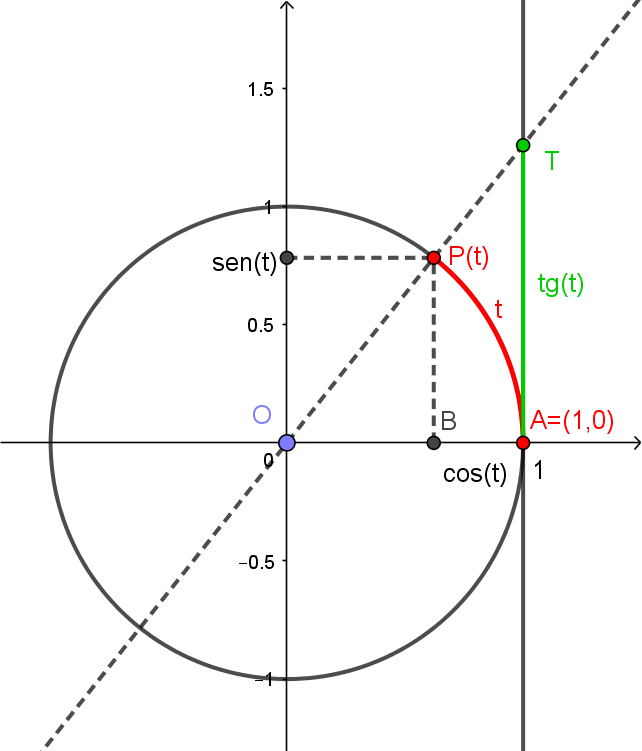
\[\frac{\overline{AT}}{\overline{BP(t)}} = \frac{\overline{OA}}{\overline{OB}},\]
Como $\overline{AT} = \mathrm{tg}(t)$, $\overline{BP(t)} = \mathrm{sen}(t)$, $\overline{OA} = 1$ e $\overline{OB}=\cos(t)$, temos
\[\frac{\mathrm{tg}(t)}{\mathrm{sen}(t)} = \frac{1}{\cos(t)},\]logo
\[\mathrm{tg}(t) = \frac{\mathrm{sen}(t)}{\cos(t)}.\]
Um detalhe sobre a tangente é que ela não está definida para todo $t$. Se, por exemplo, $t=\pi/2$, o ponto $P(t)$ estará sobre o eixo $y$ e, portanto, a reta $OP(t)$ não intersectará a reta $x=1$, portanto não existirá o ponto $T$ e a tangente. Isto acontecerá sempre que $P(t)$ estiver sobre o eixo $y$, ou seja, quando $t$ for $-\pi/2, \pi/2, 3\pi/2, 5\pi/2$ ou mais geralmente, qualquer valor da forma $\pi/2 + k\pi$, com $k\in\mathbb{Z}$. Isto é, quando $t$ for $\pi/2$ mais qualquer número de mais-voltas.
E, como as equações não mentem jamais, a expressão que deduzimos para a tangente, $\mathrm{tg}(t) = \dfrac{\mathrm{sen}(t)}{\cos(t)}$, também não está definida para tais valores de $t$, pois, para $t$ na forma $\pi/2 + k\pi$, $k \in\mathbb{Z}$, teremos $\cos(t) = 0$.
Assim, a tangente determina uma função real $\mathrm{tg}$ de domínio dado por $\{x \in \mathbb{R}:x \neq \frac{\pi}{2}+k\pi, \forall k \in \mathbb{Z}\}$, isto é, uma função
Podemos construir o gráfico da $\mathrm{tg}$ da mesma forma que foi feito com o $\mathrm{sen}$.
O gráfico da tangente é como abaixo. Repare que suas raízes são as mesmas da função $\mathrm{sen}$ e que ela não está definida para os valores de $x$ nos quais $\cos(x) = 0$.

A função $\mathrm{tg}: \left\{x \in \mathbb{R}\left| x\neq \frac{\pi}{2}+k\pi, \forall k \in \mathbb{Z}\right.\right\} \rightarrow \mathbb{R}$ tem as seguintes propriedades:
$\mathrm{tg}(-x) = -\mathrm{tg}(x)$, ou seja, $\mathrm{tg}$ é uma função ímpar.
$\mathrm{tg}(a+b) = \dfrac{\mathrm{tg}(a)+\mathrm{tg}(b)}{1 - \mathrm{tg}(a)\mathrm{tg}(b)}$, quando $\mathrm{tg}(a+b)$ estiver definida.
$\mathrm{tg}(x+\pi) = \mathrm{tg}(x)$, logo $\mathrm{tg}$ é uma função de período $\pi$.
Podemos concluir estas propriedades a partir do que já sabemos sobre as funções seno e cosseno. Temos
\[\mathrm{tg}(-x) = \frac{\mathrm{sen}(-x)}{\cos(-x)} = \frac{-\mathrm{sen}(x)}{\cos(x)} = -\frac{\mathrm{sen}(x)}{\cos(x)}=-\mathrm{tg}(x),\]e ainda,
\[\mathrm{tg}(a+b) = \frac{\mathrm{sen}(a+b)}{\cos(a+b)} = \frac{\mathrm{sen}(a)\cos(b) + \mathrm{sen}(b)\cos(a)}{\cos(a)\cos(b) - \mathrm{sen}(a)\mathrm{sen}(b)} = \frac{\frac{\mathrm{sen}(a)\cos(b) + \mathrm{sen}(b)\cos(a)}{\cos(a)\cos(b)}}{\frac{\cos(a)\cos(b) - \mathrm{sen}(a)\mathrm{sen}(b)}{\cos(a)\cos(b)}} = \]\[=\frac{\frac{\mathrm{sen}(a)}{\cos(a)} + \frac{\mathrm{sen}(b)}{\cos(b)}}{1 - \frac{\mathrm{sen}(a)\mathrm{sen}(b)}{\cos(a)\cos(b)}}=\frac{\mathrm{tg}(a)+\mathrm{tg}(b)}{1 - \mathrm{tg}(a)\mathrm{tg}(b)}.\]
Com esta relação, e lembrando que $\mathrm{tg}(0) = \frac{\mathrm{sen}(0)}{\cos(0)} = \frac{0}{1} = 0$, deduzimos a terceira propriedade:
\[\mathrm{tg}(x+\pi) = \dfrac{\mathrm{tg}(x)+\mathrm{tg}(\pi)}{1 - \mathrm{tg}(a)\mathrm{tg}(\pi)} = \dfrac{\mathrm{tg}(x)+0}{1 - \mathrm{tg}(a)\cdot 0} = \frac{\mathrm{tg}(x)}{1} = \mathrm{tg}(x).\]
Se $\mathrm{tg}(\theta) = \displaystyle\frac{15}{8}$, quais são as possibilidades para $\cos(\theta)$ e $\mathrm{sen}(\theta)$ ?
Como
\[\frac{\mathrm{sen}(x)}{\cos(x)} = \mathrm{tg}(x) = \displaystyle\frac{15}{8} \therefore \mathrm{sen}(x) = \frac{15}{8}\cos(x),\]e, como
\[\mathrm{sen}^2(x) + \cos^2(x) = 1,\]temos
\[\left(\frac{15}{8}\cos(x)\right)^2 + \cos^2(x) = 1,\]logo
\[\frac{225\;\cos^2(x)}{64} + \cos^2(x) = 1,\]e então
\[\frac{289\;\cos^2(x)}{64} = 1.\]Com isso,
\[\cos^2(x) = \frac{64}{289}.\]Assim,
\[\cos(x) = \frac{8}{17}\;\;\textnormal{ ou }\;\;\cos(x) = -\frac{8}{17}.\]Se $\cos(x) = \frac{8}{17}$, temos
\[\mathrm{sen}(x) = \frac{15}{8}\cdot \frac{8}{17} = \frac{15}{17}.\]Se, por outro lado, $\cos(x) = -\frac{8}{17}$, temos
\[\mathrm{sen}(x) = \frac{15}{8}\cdot \left(-\frac{8}{17}\right) = -\frac{15}{17}.\]Assim, temos duas possibilidades
\[\cos(x) = \frac{8}{17} \text{ e } \mathrm{sen}(x) = \frac{15}{17}\]\[\text{ou}\]
\[\cos(x) = -\frac{8}{17} \text{ e } \mathrm{sen}(x) = -\frac{15}{17}.\]
Determine todos os valores de $x \in \mathbb{R}$ tais que
\[\mathrm{tg}(x) \geqslant \sqrt{3}.\]
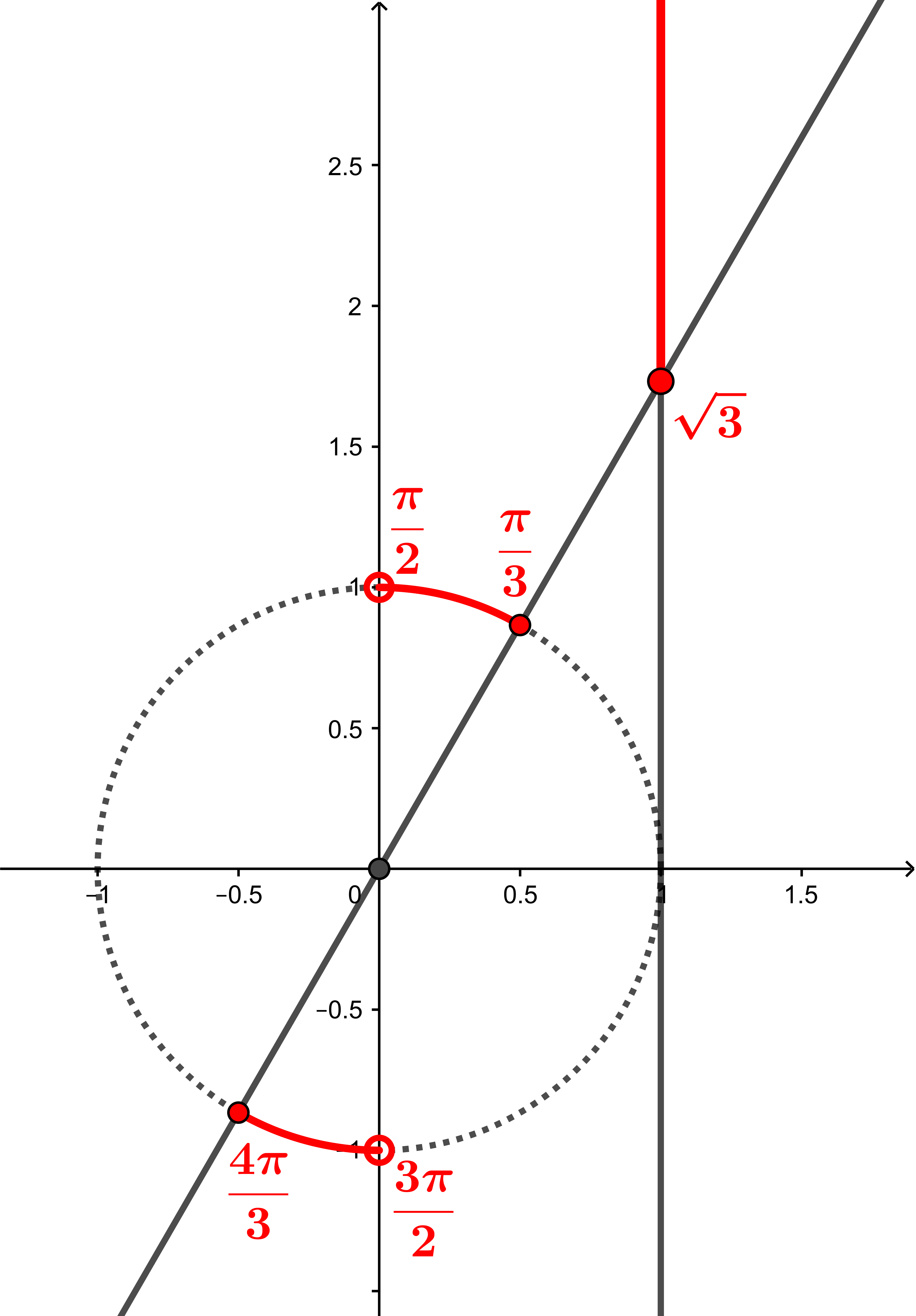
Como $\mathrm{tg}\left(\frac{\pi}{3}\right) = \mathrm{tg}\left(\frac{4\pi}{3}\right) = \sqrt{3}$, vemos, no círculo trigonométrico, que $\mathrm{tg}(x) \geqslant \sqrt{3}$ se, e somente se,
\[\frac{\pi}{3} + 2k\pi \leqslant x < \frac{\pi}{2}+2k\pi \;\textnormal{ ou }\; \frac{4\pi}{3} + 2k\pi \leqslant x < \frac{3\pi}{2} + 2k\pi, \;\;k\in \mathbb{Z}.\]
De forma semelhante à tangente, definimos a cotangente de $t$, denotada por $\mathrm{cotg}(t)$. Na figura abaixo, $\mathrm{cotg}(t)$ é a coordenada $x$ do ponto $T$.
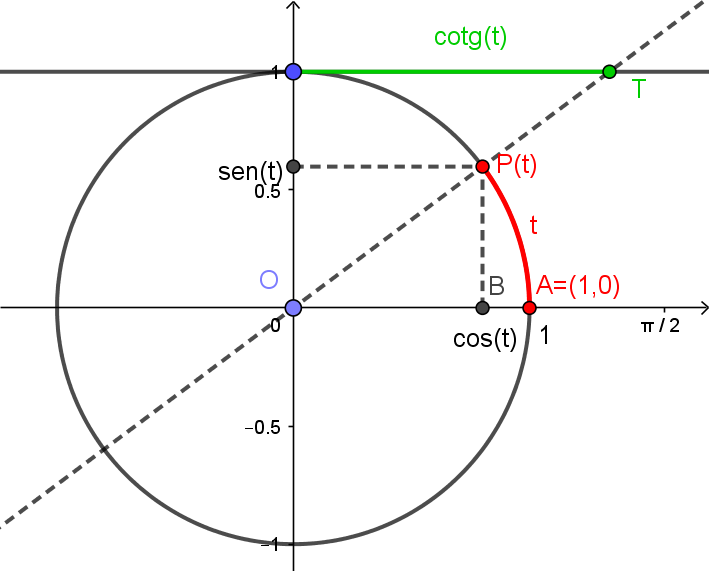
Procedendo como na tangente, através da semelhança de triângulo, podemos concluir que
\[\mathrm{cotg}(t) = \frac{\cos(t)}{\mathrm{sen}(t)},\]definida quando $t$ não for da forma $k\pi$, com $k \in \mathbb{Z}$. Teremos então a função real
\[\mathrm{cotg}: \left\{x \in \mathbb{R}\left.:x\neq k\pi, \forall k \in \mathbb{Z}\right.\right\} \rightarrow \mathbb{R},\;\mathrm{cotg}(x) = \frac{\cos(x)}{\mathrm{sen}(x)}.\]A cotangente tem as propriedades semelhantes à tangente:
A função $\mathrm{cotg}: \left\{x \in \mathbb{R}\left.:x\neq k\pi, \forall k \in \mathbb{Z}\right.\right\} \rightarrow \mathbb{R}$ tem as seguintes propriedades:
$\mathrm{cotg}(-x) = -\mathrm{cotg}(x)$, ou seja, $\mathrm{cotg}$ é uma função ímpar.
$\mathrm{cotg}(x+\pi) = \mathrm{cotg}(x)$, logo $\mathrm{cotg}$ é uma função de período $\pi$.
O gráfico da função $\mathrm{cotg}$ é dado abaixo.

Considere agora uma reta tangente ao círculo no ponto $P(t)$ e os pontos $E$ e $F$ de interseção desta reta com os eixos $x$ e $y$, respectivamente, como na figura abaixo.
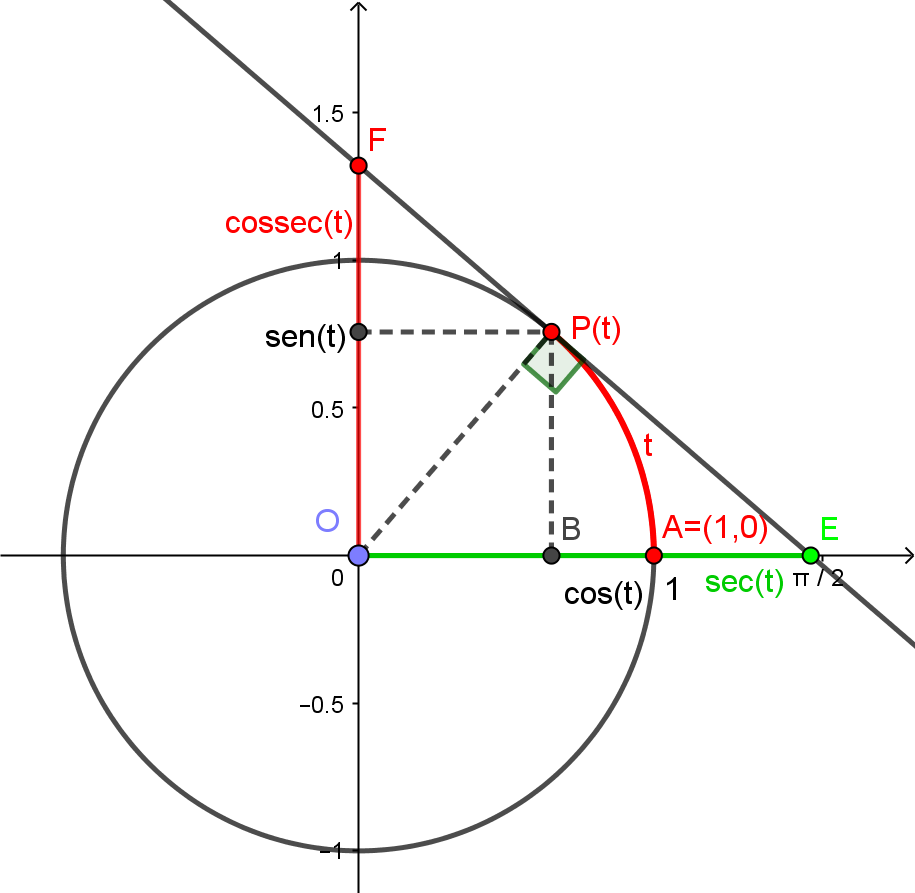
Definimos a secante e a cossecante de $t$ como sendo, respectivamente, a coordenada $x$ do ponto $E$ e a coordenada $y$ do ponto $F$. A partir da semelhança entre os triângulos $EOF$ e $EP(t)O$, concluímos que
\[\sec(t)=\frac{1}{\cos(t)}\]e que $\sec$ está definida sempre que $t \neq \frac{\pi}{2} + k\pi$ para todo $k\in\mathbb{Z}$. A partir da semelhança entre os triângulos $EOF$ e $FP(t)O$, concluímos que
\[\mathrm{cossec}(t)=\frac{1}{\mathrm{sen}(t)}\] e que $\mathrm{cossec}$ está definida sempre que $t \neq t\pi$ para todo $k\in\mathbb{Z}$.
Temos então as funções reais
\[\mathrm{cossec}: \left\{x \in \mathbb{R}\left.: x \neq k\pi, \forall k \in \mathbb{Z}\right.\right\} \rightarrow \mathbb{R},\; \cos(x) = \frac{1}{\mathrm{sen}(x)}\;.\]
A função $\sec$ tem as seguintes propriedades:
$\sec(-x) = \sec(x)$, ou seja, $\sec$ é uma função par.
$\sec(x+2\pi) = \sec(x)$, logo $\sec$ é uma função de período $2\pi$.
$\sec(x) \geqslant 1$ ou $\sec(x) \leqslant -1$ para todo $x \in \mathbb{R}$
O gráfico da função $\sec$ é dado abaixo.

A função $\mathrm{cossec}$ tem as seguintes propriedades:
$\mathrm{cossec}(-x) = -\mathrm{cossec}(x)$, ou seja, $\sec$ é uma função par.
$\mathrm{cossec}(x+2\pi) = \mathrm{cossec}(x)$, logo $\sec$ é uma função de período $2\pi$.
$\mathrm{cossec}(x) \geqslant 1$ ou $\mathrm{cossec}(x) \leqslant -1$ para todo $x \in \mathbb{R}$
O gráfico da função $\mathrm{cossec}$ é dado abaixo.
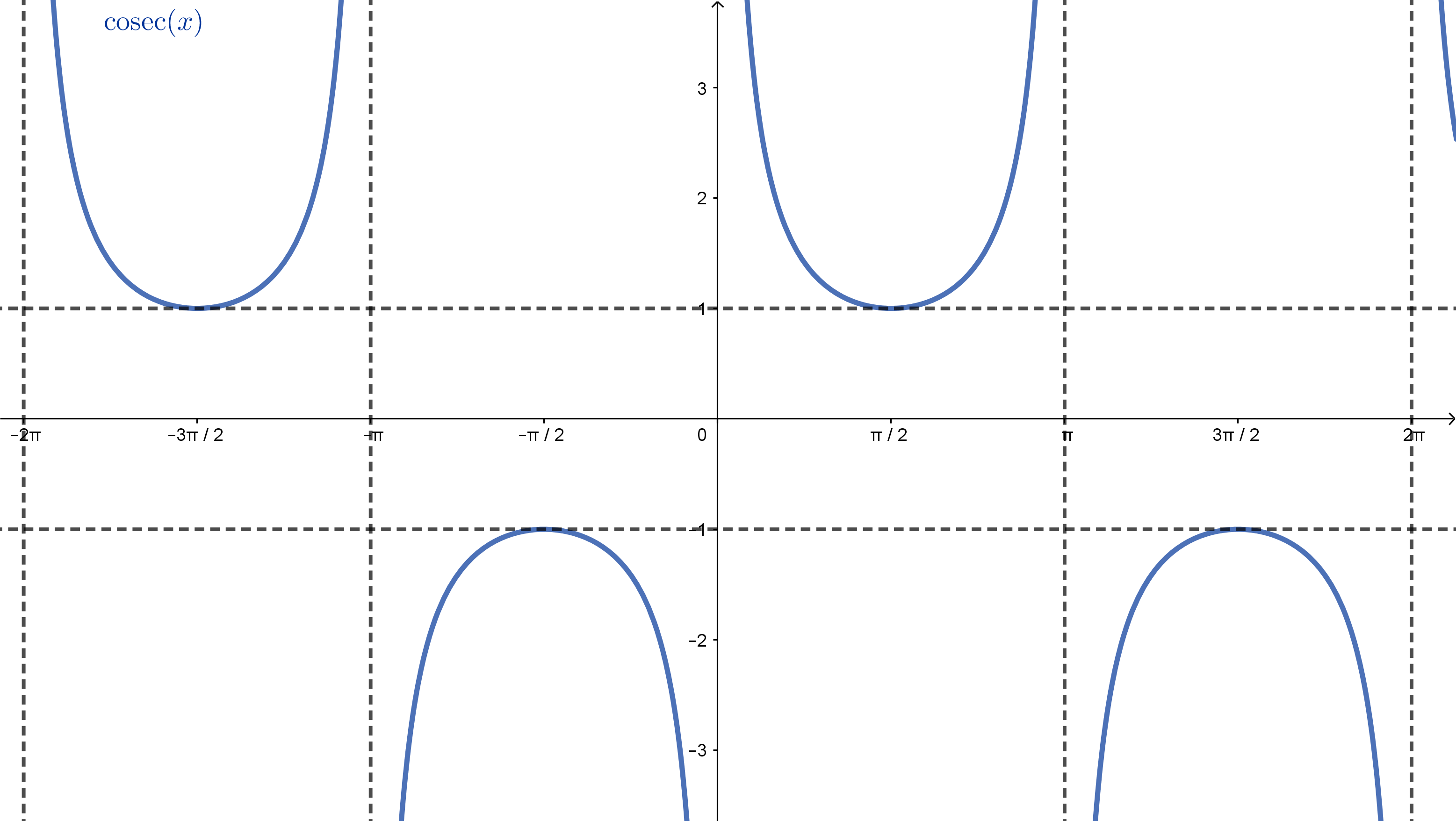
Observe que
\[|\sec(x)| = \left|\frac{1}{\cos(x)}\right| = \frac{1}{|\cos(x)|},\]logo, como $0 < |\cos(x)| \leqslant 1$ para todo $x$ onde $\sec(x)$ está definido, temos
\[|\sec(x)| \geqslant 1,\]ou seja, $\sec(x) \leqslant -1$ ou $\sec(x) \geqslant 1$. Da mesma forma, $|\mathrm{cossec}(x)| \geqslant 1$, ou seja, $\mathrm{cossec}(x) \leqslant -1$ ou $\mathrm{cossec}(x) \geqslant 1$.