
Observe a função $f:\mathbb{R} \rightarrow \mathbb{R}$ de expressão $f(x) = x^4 - 2x^2 + 1$. Vamos avaliar $f$ em alguns valores de $x$:
$f(1) = 1^4 - 2\cdot 1^2 - 1 = -2$
$f(2) = 2^4 - 2\cdot 2^2 - 1 = 5$
$f(3) = 3^4 - 2\cdot 3^2 - 1 = 62$
$f(-1) = (-1)^4 - 2\cdot (-1)^2 - 1 = -2$
$f(-2) = (-2)^4 - 2\cdot (-2)^2 - 1 = 5$
$f(-3) = (-3)^4 - 2\cdot (-3)^2 - 1 = 62.$
Percebemos que a função assume o mesmo valor nos pontos simétricos escolhidos acima, isto é, $f(-1) = f(1)$, $f(2) = f(-2)$, $f(3) = f(-3)$. Indo mais além, podemos ver que, para todo $x \in \mathbb{R}$, $f(x) = f(-x)$. De fato,
\[f(-x) = (-x)^4 - 2(-x)^2 + 1 = x^4 - 2x^2 + 1 = f(x).\]O gráfico desta função é dado por
No applet acima, mova o ponto $(x,y)$ do gráfico de $f$ e observe como $(-x,y)$ também pertencerá ao gráfico. O gráfico será então simétrico em relação ao eixo $y$. E por que será que isto acontece?
Um ponto $(x,y)$ pertence ao gráfico se, e somente se, $y = f(x)$. Como $f(-x)=f(x)$, o ponto $(-x,f(x)) = (-x,y)$ também pertencerá ao gráfico. Assim, o gráfico é simétrico em relação ao eixo $y$.
Marcando a caixa $\cos(x)$ do applet, você pode experimentar também com a função cosseno e perceber que seu gráfico também é simétrico em relação ao eixo $y$.
Outros exemplos de funções em que este fenômeno acontece são a função modular e o cosseno, pois, como já vimos, $\cos(-x) = \cos(x)$ e $|-x| = |x|$.
Uma função $f:\mathrm{D}\rightarrow C$ é par se, para todo $x \in \mathrm{D}$,
\[f(-x) = f(x).\]
A definição acima traz uma sutileza. O domínio $\mathrm{D}$ da função deverá ser simétrico, isto é, se um número real $x$ pertencer ao domínio, seu simétrico $-x$ também deverá pertencer.
E quando uma função não é par? Note que, para ser par, devemos ter $f(-x) = f(x)$ para todo $x$ no domínio. Assim, ela não será par se existir pelo menos um $x \in \mathrm{D}$ para o qual $f(-x)\neq f(x)$.
Um fato importante sobre as funções pares é que seu gráfico é simétrico em relação ao eixo $y$. Como vimos acima, se uma função é par, temos $f(-x) = f(x)$, logo os pontos $(x, f(x))$ e $(-x,f(x))$ pertencem ao gráfico da função. E estes pontos são simétricos em relação ao eixo $y$, pois são da forma $(x,y)$ e $(-x,y)$, isto é, mesma coordenada vertical $y$ e coordenadas horizontais $x$ e $-x$ simétricas.
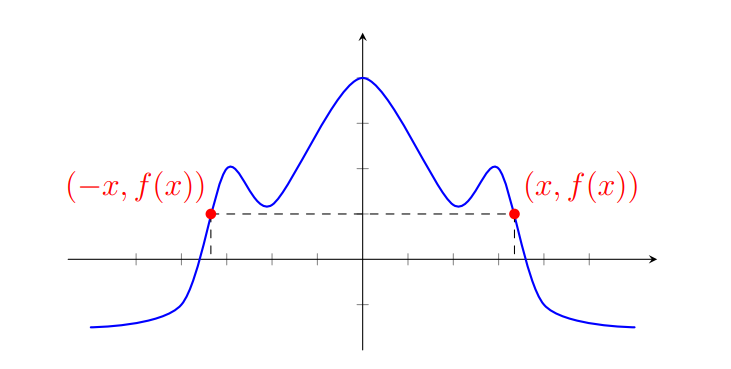
É como se o gráfico fosse "espelhado" em relação ao eixo $y$. Veremos exemplos abaixo para analisar quais das funções são pares.
$\displaystyle f: \mathbb{R} \rightarrow \mathbb{R},\;f(x) = 1-x^4$ Dado $x \in \mathbb{R}$, como $(-x)^4 = x^4$, temos
\[f(-x) = 1 - (-x)^4 = 1- x^4 = f(x).\]Assim, $f$ é uma função par.

Repare que o gráfico de $f$, em azul, é simétrico em relação ao eixo $y$ e coincide com o da função definida por $f(-x)$, tracejado em laranja.
$\displaystyle g: \mathbb{R}^{*} \rightarrow \mathbb{R},\;g(x) = x - \frac{1}{x^2}$ Se tomarmos um $x \in \mathbb{R}^{*}$, como $(-x)^2 = x^2$, teremos
\[\displaystyle g(-x) = (-x) = \frac{1}{(-x)^2} = -x - \frac{1}{x^2}.\]Esta expressão não é necessariamente igual a $g(x)$. Escolhendo um valor para $x$, por exemplo, $x=1$, teremos
\[g(1) = 1 - \frac{1}{1^2} = 0 \;\;\textnormal{ e }\;\;g(-1) = -1 - \frac{1}{(-1)^2} = -2,\]e então $g(-1) \neq g(1)$. Com isso, para pelo menos um número real $x$, temos $g(x)\neq g(-x)$, logo a função não é par.
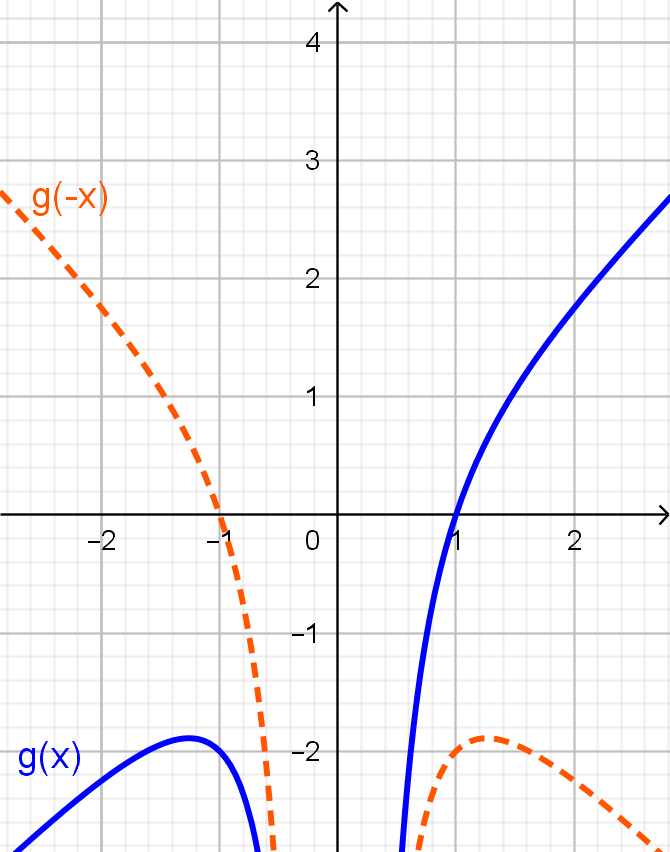
Repare que o gráfico de $g$, em azul, não é simétrico em relação ao eixo $y$ e não coincide com o da função definida por $g(-x)$, tracejado em laranja.
$\displaystyle h: \mathbb{R}^{*} \rightarrow \mathbb{R},\;h(x) = |x| - \frac{1}{x^2}$ Se tomarmos um $x \in \mathbb{R}^{*}$, como $(-x)^2 = x^2$ e $|-x| = |x|$, teremos
\[\displaystyle h(-x) = |-x| = \frac{1}{(-x)^2} = |x| - \frac{1}{x^2} = g(x).\] Logo, $h$ é uma função par.
Atenção! Repare que não escrevemos que $|-x| = x$, pois isto pode não ser verdadeiro. Se $x=-1$, por exemplo, $|-x| = |-(-1)| = 1 \neq -1 = x$. Podemos apenas garantir o que escrevemos acima, que $|-x| = |x|$. Em momento algum foi dito que $x$ era positivo e $-x$ negativo.

Repare que o gráfico de $h$, em azul, é simétrico em relação ao eixo $y$ e coincide com o da função definida por $h(-x)$, tracejado em laranja.
$\displaystyle i: \mathbb{R} \rightarrow \mathbb{R},\;i(x) = x^3 - x + 1$
Se tomarmos um $x \in \mathbb{R}$, teremos
\[i(-x) = (-x)^3 - (-x) + 1 = -x^3 + x + 1,\]que não necessariamente é igual a $i(x) = x^3 - x + 1$. Por exemplo, tomando $x=1$, temos
\[i(-1) = (-1)^3 - (-1) + 1 = -1 + 1 + 1 = 1 \;\;\textnormal{ e }\;\;i(1) = 1^3 - 1 + 1 = 1.\] Eiii! Obtivemos que $i(-1) = i(1)$! Mas o que isso significa?
Nada! Isso não significa que $i$ seja par. Para ser par, $i(-x)$ deve ser igual a $i(x)$ para todo $x$ no domínio, $\mathbb{R}$. O fato de ter acontecido para $x=1$ é mera coincidência. Vejamos agora para $x=2$:
ou seja, $i(-2) \neq i(2)$, o que garante que $i$ não é uma função par.
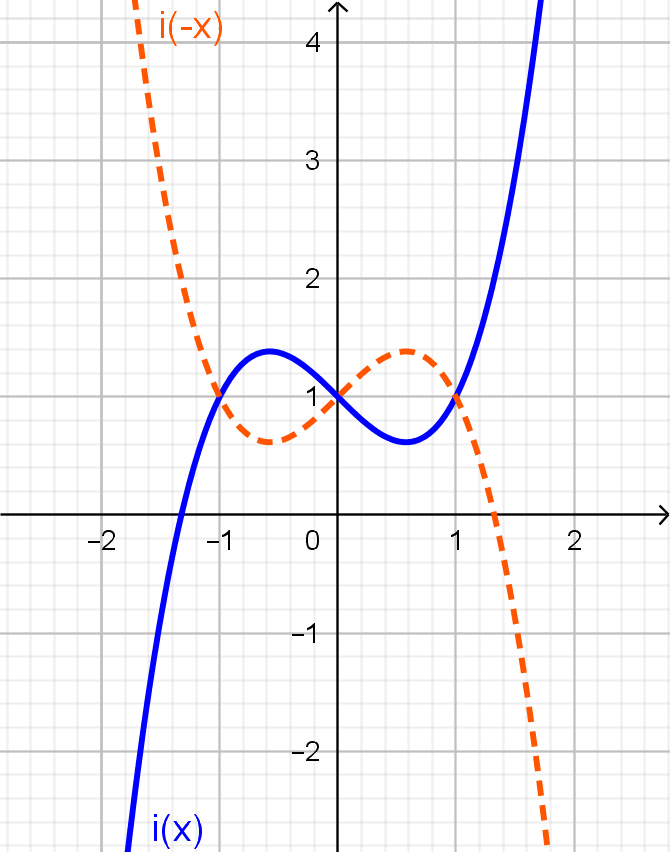
Repare que o gráfico de $i$, em azul, não é simétrico em relação ao eixo $y$ e não coincide com o da função definida por $i(-x)$, tracejado em laranja.
Alguns exemplos conhecidos de funções pares:
Função modular $f(x)=|x|$.
Função cosseno $f(x)=\cos(x)$, função secante $f(x)=\sec(x)$.
Funções polinomiais que só tenham expoentes pares e termo independente.
Seja $f:\mathbb{R} \rightarrow \mathbb{R}$ definida por $f(x) = x^3 - x$. Como $(-x)^3 = -x^3$ para todo número real $x$, temos,
\[f(-x) = (-x)^3 - (-x) = -x^3 + x = -(x^3 - x) = -f(x).\] Assim, para todo $x \in \mathbb{R}$, $f(-x) = - f(x)$.
Funções como esta serão chamadas de ímpares, como veremos mais abaixo.
Observe abaixo o gráfico da função $f$ e note que ele é simétrico em relação à origem, isto é, o ponto $(x,y)$ pertence ao gráfico se, e somente se, o ponto $(-x,-y)$ também pertence.
No applet acima, mova o ponto $(x,y)$ do gráfico de $f$ e observe como $(-x,-y)$ também pertencerá ao gráfico. Lembre-se que, se $(x,y)$ é um do gráfico, teremos $y=f(x)$. Como $f(-x) = -f(x) = -y$, o ponto $(-x, f(-x)) = (-x, -y)$ pertence ao gráfico.
Uma função $f:\mathrm{D}\rightarrow C$ é ímpar se, para todo $x \in \mathrm{D}$,
\[f(-x) = -f(x).\]
Como no caso da função par, esta definição implica que o domínio $\mathrm{D}(f)$ da função deverá ser simétrico, isto é, se um número real $x$ pertencer ao domínio, seu simétrico $-x$ também deverá pertencer. Quando uma função não é ímpar? Para ser ímpar, devemos ter $f(-x) = -f(x)$ para todo $x$ no domínio. Assim, ela não será ímpar se existir pelo menos um $x \in \mathrm{D}$ para o qual $f(-x)\neq -f(x)$. Como vimos no exemplo acima, o gráfico de uma função ímpar é simétrico em relação à origem. Dois pontos são simétricos em relação à origem se forem da forma $(x,y)$ e $(-x,-y)$ e, no caso de uma função ímpar, teremos ambos os pontos $(x, f(x))$ e $(-x,f(-x))=(-x,-f(x))$ no gráfico da função.
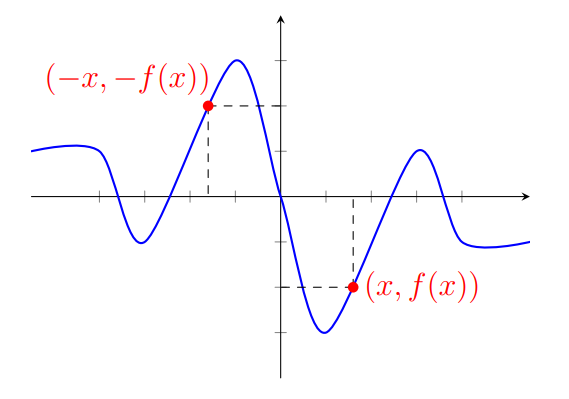
É como se o gráfico não se alterasse caso fosse "rotacionado $180^\circ$" em relação à origem. Dito de outra forma: podemos refletir em torno do eixo$y$ e depois em torno do eixo $x$ que fica inalterado. Veremos exemplos logo abaixo.
$\displaystyle f: \mathbb{R}^{*} \rightarrow \mathbb{R},\;f(x) = x|x| - \frac{1}{x}.$ Dado $x \in \mathbb{R}^{*}$, temos
\[f(-x) = (-x)|-x| - \frac{1}{-x} = -x|x| + \frac{1}{x} = - \left(x|x| - \frac{1}{x}\right) = -f(x).\]Assim, $f$ é uma função ímpar.

Repare que o gráfico de $f$, em azul, é simétrico em relação à origem e coincide com o da função definida por $-f(-x)$, tracejado em laranja.
$\displaystyle g: \mathbb{R} \rightarrow \mathbb{R},\;g(x) = x + 1.$ Se tomarmos um $x \in \mathbb{R}$, teremos
\[\displaystyle g(-x) = (-x) + 1 = -x + 1.\]Esta expressão não é necessariamente igual a $g(x)$. Escolhendo um valor para $x$, por exemplo, $x=1$, teremos
\[g(1) = 1 + 1 = 2 \;\;\textnormal{ e }\;\;g(-1) = -1 + 1 = 0,\]e então $g(-1) \neq g(1)$. Com isso, para pelo menos um número real $x$, temos $g(x)\neq g(-x)$, logo a função não é ímpar.
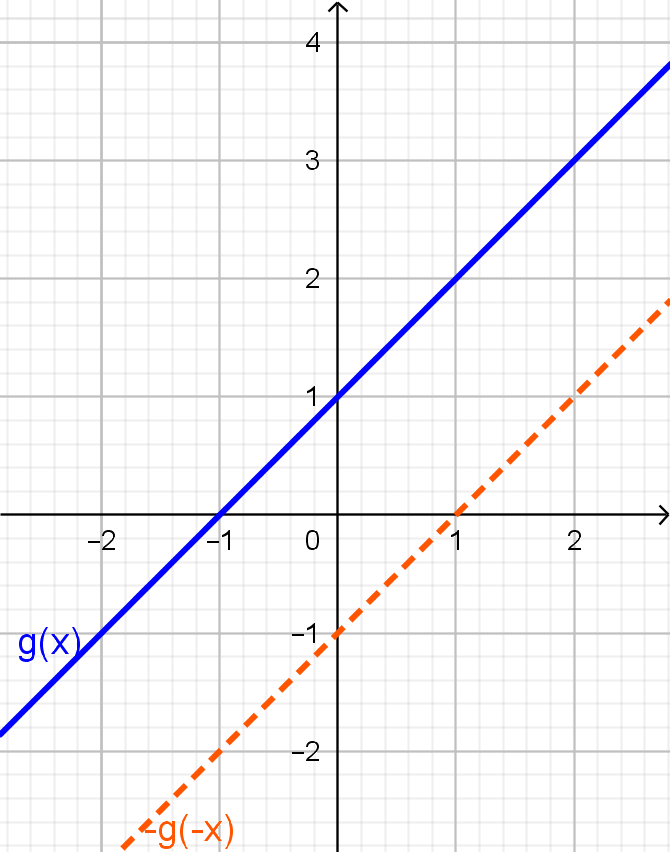
Repare que o gráfico de $g$, em azul, não é simétrico em relação à origem e não coincide com o da função definida por $-g(-x)$, tracejado em laranja.
$\displaystyle h: \mathbb{R} \rightarrow \mathbb{R},\;h(x) = x + \mathrm{sen}(x).$ Se tomarmos um $x \in \mathbb{R}$, como $\mathrm{sen}(-x) - \mathrm{sen}(x)$, teremos
\[\displaystyle h(-x) = (-x) + \mathrm{sen}(-x) = -x - \mathrm{sen}(x) = -(x + \mathrm{sen}(x)) = -h(x).\] Logo, $h$ é uma função ímpar.
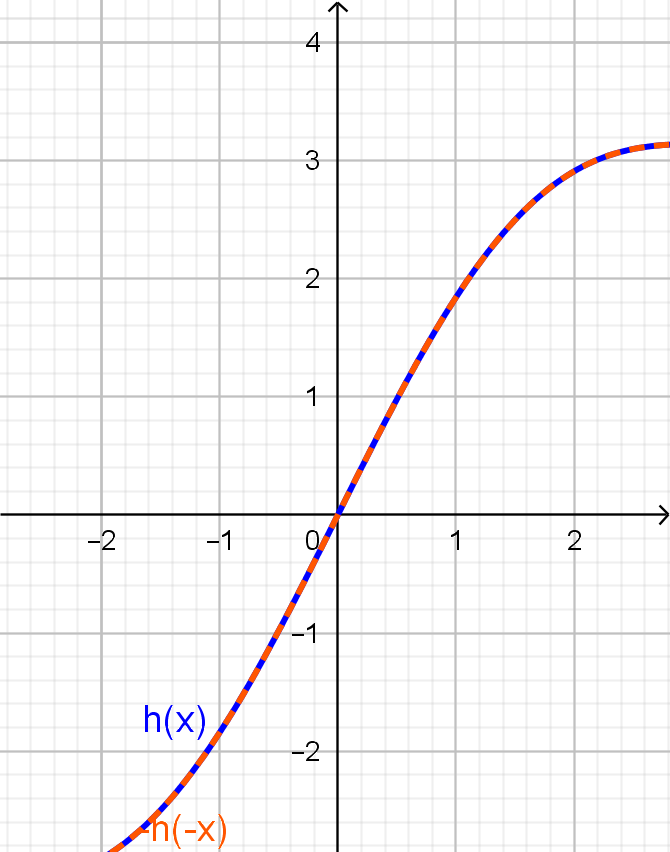
Repare que o gráfico de $h$, em azul, é simétrico em relação à origem e coincide com o da função definida por $-h(-x)$, tracejado em laranja.
$\displaystyle i: \mathbb{R} \rightarrow \mathbb{R},\;i(x) = x^3 - x^2 + 1.$
Se tomarmos um $x \in \mathbb{R}$, teremos
\[i(-x) = (-x)^3 - (-x)^2 + 1 = -x^3 -x^2 + 1,\]que não necessariamente é igual a $-i(x) = -(x^3 - x^2 + 1) = -x^3 + x^2 - 1$. Por exemplo, tomando $x=1$, temos
\[i(-1) = (-1)^3 - (-1)^2 + 1 = -1 - 1 + 1 = - 1 \;\;\textnormal{ e }\;\;i(1) = 1^3 - 1^2 + 1 = 1.\]Obtivemos que $i(-1) = -1 = -i(1)$! E o que isso significa? Novamente, nada! Isso não significa que $i$ seja ímpar. Para ser ímpar, $i(-x)$ deve ser igual a $-i(x)$ para todo $x$ no domínio, $\mathbb{R}$. O fato de ter acontecido para $x=1$ é mera coincidência. Vejamos agora para $x=2$:
\[i(-2) = (-2)^3 - (-2)^2 + 1 = -8 - 4 + 1 = -11 \;\;\textnormal{ e }\;\;i(2) = 2^3 - 2^2 + 1 = 5,\]ou seja, $i(-2) \neq -i(2)$, o que garante que $i$ não é uma função ímpar.
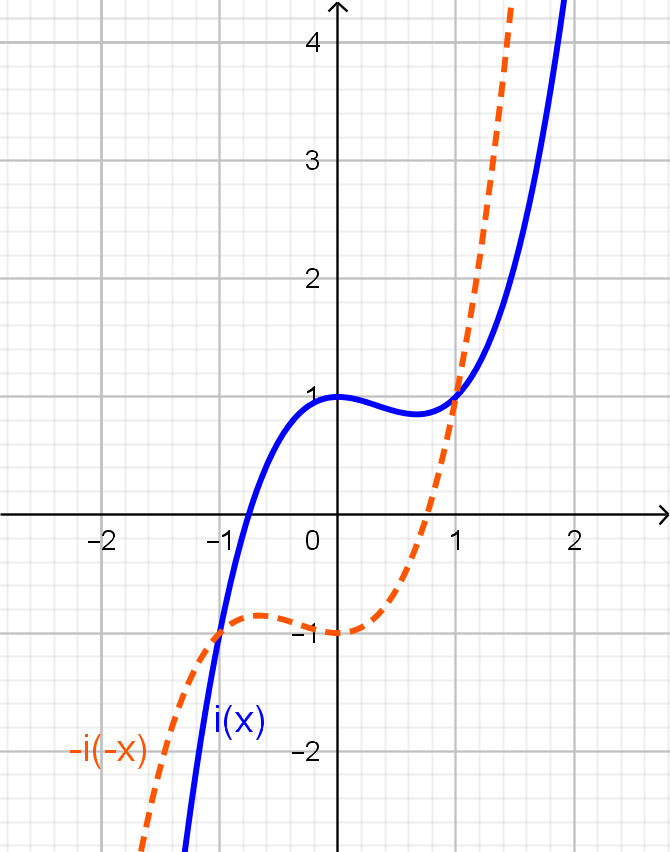
Repare que o gráfico de $i$, em azul, não é simétrico em relação à origem e não coincide com o da função definida por $-i(-x)$, tracejado em laranja.
Alguns exemplos conhecidos de funções ímpares:
Função seno, função tangente, função cotangente, função cossecante.
Funções polinomiais que só tenham expoentes ímpares e não tenham termo independente.
Observações importantes:
Se uma função $f$ é ímpar e existe $f(0)$ então, necessariamente, teremos $f(0) = 0$. Note que $0=-0$, logo $f(0) = f(-0)$; porém, como $f$ é ímpar, $f(-0) = -f(0) = -f(-0)$. Assim, $f(0) = - f(0)$, logo $2f(0) = 0$ e, então $f(0) = 0$.
Uma função não tem que ser par ou ímpar! Na verdade, a grande maioria das funções não será nem par e nem ímpar. Um exemplo é a função $f:\mathbb{R}\rightarrow\mathbb{R}$, $f(x) = x+1$.
Existe uma função par e ímpar ao mesmo tempo, é a função $f:\mathbb{R}\rightarrow\mathbb{R}$, $f(x)=0$.