
Nas seções anteriores, foram apresentadas algumas funções elementares e seus gráficos. Agora pretendemos apresentar como podemos obter novas funções mais elaboradas, recorrendo à composição de funções. Vejamos um exemplo onde temos uma aplicação da composição de funções.
Suponha que recebeu um vale de $R\$40$ para gastar numa livraria. A função que descreve o valor a pagar usando o vale é $f(x)=x-40$. Mas no dia que escolhe ir à livraria, eles estão oferecendo um desconto de $30\%$ em todos os livros de cálculo. A função que descreve o desconto desse dia é $g(x)=x-0,3x=0,7x$. A livraria permite deixar o cliente escolher qual a ordem para aplicar o desconto, ou seja você deve escolher entre considerar a função custo $f \circ g$ ou $g \circ f$.
Note que $(f \circ g)(x)=f(0,7x)=0,7x-40$ e $(g \circ f)(x)=g(x-40)=0,7(x-40)=0,7x-28$.
Então o comprador deve escolher a opção de custo dada por $f \circ g$
Dadas duas ou mais funções podemos combiná-las usando diversas operações, obtendo novas funções.
Se considerarmos duas funções $f$ e $g$ podemos por exemplo definir as funções $f+g$, $f-g$, $fg$ e $f/g$ que correspondem à soma, subtração, produto e quociente de funções, respectivamente. Além destas operações, podemos também usar a composição de funções. A composição de duas funções consiste em aplicar uma das funções e depois aplicar a outra função à imagem obtida após a aplicação da primeira função. Ou seja, dadas duas funções $f$ e $g$, podemos aplicar $g$ a um certo valor de $x$ (pertencente ao domínio de $g$ e depois aplicar $f$ a $g(x)$, caso $g(x)$ esteja no domínio de $f$.
Dadas duas funções $f$ e $g$, a função composta $f \circ g$ é definida por
$$(f \circ g)(x)= f(g(x)),$$sendo o seu domínio o conjunto $\mathrm{D}(f\circ g)=\left\{ x \in \mathrm{D}(g): g(x) \in \mathrm{D}(f) \right\}$.
Também podemos denominar $f \circ g$ por composição de $f$ e $g$. O esquema abaixo ilustra a definição da composição $f \circ g$:
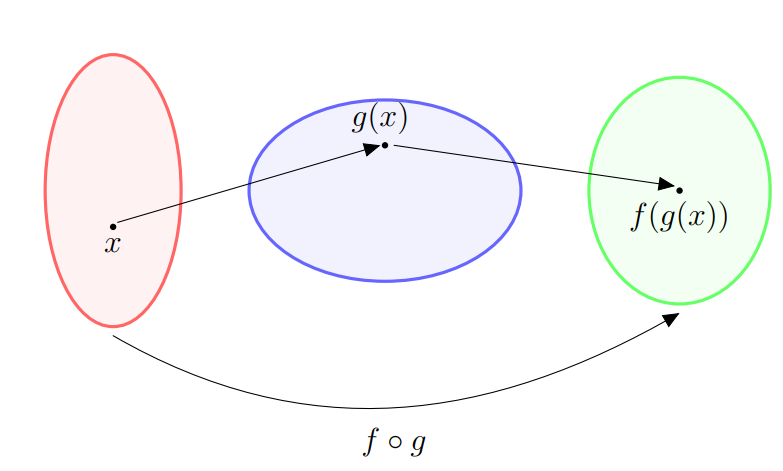
Observação: A operação composição de funções não é comutativa, ou seja, em geral $f \circ g$ é diferente de $g \circ f$. Por exemplo, se para $x \in \mathbb{R}$ considerarmos $f(x)=x^2$ e $g(x)=x+3$, então $(f \circ g)(x)= f(x+3)=(x+3)^2$ e $(g \circ f)(x)= g(x^2)=x^2+3$, ambas com domínio $\mathbb{R}$.
A função $\displaystyle h(x) = \sqrt{1+x^2}$ é a composição das funções $\displaystyle f(x) = \sqrt{x}$ e $\displaystyle g(x) = 1+x^2$, ou seja, $h=f \circ g$. Observe que a $Im(g)=[1, \infty)$ está contida em $\mathrm{D}(f)=[0, + \infty)$, logo $\mathrm{D}(f \circ g)=\mathrm{D}(g)=\mathbb{R}$.
A função $\displaystyle h(x) = \frac{1}{2+|x|}$ é a composição das funções $\displaystyle f(x) = \frac{1}{x}$, $x\neq 0$ e $\displaystyle g(x) = 2+|x|$, $x \in \mathbb{R}$, ou seja, $h=f \circ g$. Observe que a $Im(g)=[2, \infty)$ que está contido $\mathrm{D}(f)=\mathbb{R} - \{0\}$, portanto $\mathrm{D}(f \circ g)=\mathbb{R}$.
Nem sempre é possível escolher duas funções ao acaso e tentar determinar a composição das duas. Para que a função $f \circ g$ esteja bem definida é necessário que a imagem de $g$ esteja contida no domínio de $f$, ou seja $Im(g) \subset \mathrm{D}(f)$.
Consideremos as funções $f(x)=\sqrt{x}$ e $g(x)=-x^4$. Neste caso, $f \circ g$ não está definida em $\mathbb{R}$ (que é o domínio de $g$), pois a $Im(g)=(- \infty, 0]$ e $\mathrm{D}(f)=[0,+ \infty)$ portanto $f \circ g$ estaria definida apenas em $x=0$.
Consideremos as funções
$$\begin{array}{ccccc}\begin{array}{cccc}f: & \mathbb{R} & \to & [-4, +\infty ) \\& x & \mapsto & x^2 -4\end{array}& & \text{e} & &\begin{array}{cccc}g: & [0, + \infty) & \to & \mathbb{R} \\& x & \mapsto & \sqrt{x}\end{array}\end{array}$$Para determinarmos o domínio de $g \circ f$ precisamos considerar os valores de $x$ tais que $f(x)$ pertença ao domínio de $g$, ou seja, serão os valores tais que $x^2-4 \geq 0$, ou seja, $x \in (-\infty, -2] \cup [2, +\infty )$. Nesse caso a função $g \circ f$ está definida por $(g \circ f)(x)=g(f(x))=g(x^2-4)=\sqrt{x^2-4}$.