
Antes de prosseguir nesta seção, assista ao vídeo abaixo.
| Vemos o gráfico de três exemplos importantes envolvendo um denominador quetende a zero. Observe que nos três exemplos aparece um 0 em algum denominador. Cada um desses exemplos ilustrauma situação diferente. |
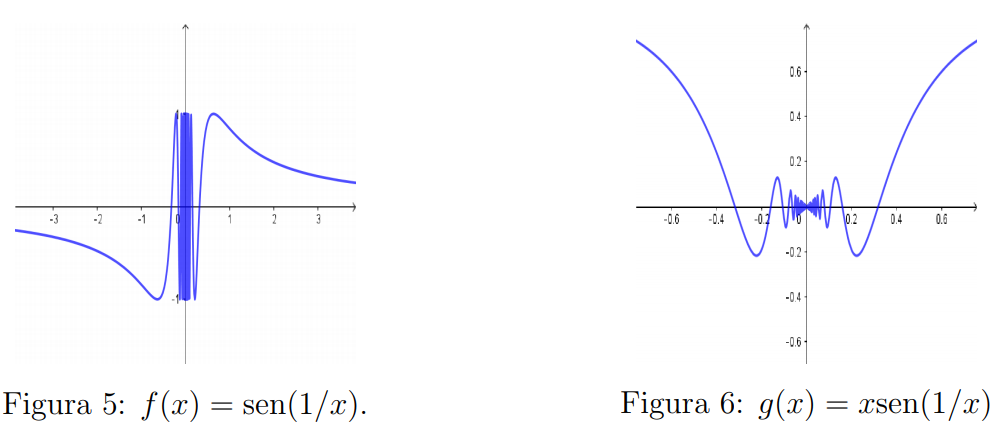 |
Nosso primeiro foco é analisar esse limite. Quando $x$ tende a $0$, tanto $x$ como $\mathrm{sen}(x)$ tendem a $0$ e não há, aqui, um modo simples de tentar simplificar essa fração. A tentativa será proceder analisando gráficos. Olhando a Figura ??? podemos imaginar que o limite deve ser $1$, o que significaria que, muito perto de $0$, o comprimento de um arco ($x$) e o valor do seu seno estão muito próximos, é razoável, então, tentar comparar os gráficos de $f(x) = x$ e $f(x) = \mathrm{sen}(x)$ .
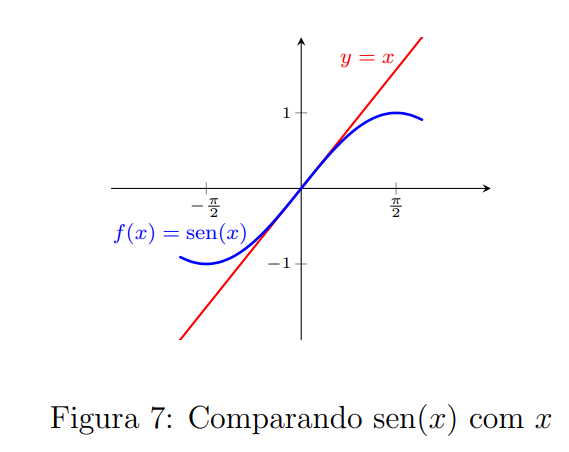
O gráfico de y = x está em vermelho e o do seno em azul. Não é difícil ver que os valores, perto da origem, são tão próximos que mal se distingue um gráfico do outro.
Uma outra tentativa, ainda no campo de uma análise gráfica, é olhar para o círculo trigonométrico.
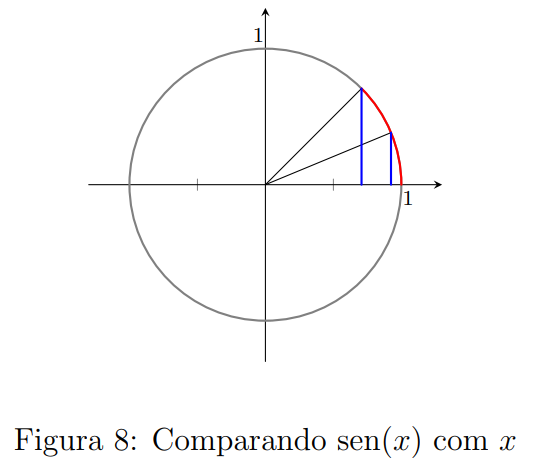
Em azul, temos o tamanho do seno; em vermelho, o arco. é possível ver que quanto menor o arco, mais próximos estão o tamanho do seno e o comprimento do arco. uma situação diferente.
A análise das figuras ???, ??? e ??? nos dá um bom motivo para apresentar aquele que é conhecido como Limite Trigonométrico Fundamental:
\[\displaystyle\lim_{x \rightarrow 0} \frac{\mathrm{sen} (x)}{x} = 1\]Até o momento, não dispomos de ferramentas teóricas suficientes para apresentar uma prova formal desse resultado. Vamos seguir acreditando, todavia, que a demonstração existe e que será vista no momento possível.
Calcular $\displaystyle\lim_{x\rightarrow 0} \frac{\mathrm{tg}(x)}{x}$.
Calcular $\displaystyle\lim_{x\rightarrow 0} {\frac{\mathrm{sen}(2x)}{x}}$.
Aqui, podemos usar o recurso de mudar a variável. Vamos escolher uma nova variável $u$ e relacioná-la com $x$ pela expressão $ u = 2x$. Então, quando $x$ tende a $0$, $u$ também tende a $0$ e reescrevemos o problema em função de $u$ como:
\[\displaystyle\lim_{u\rightarrow 0} \frac{\mathrm{sen}(u)}{\frac{u}{2}} = \displaystyle \lim_{u \rightarrow 0}2. \frac{\mathrm{sen}(u)}{u} = 2\]Um segundo exemplo importante é a função cujo gráfico está na Figura ???.
O gráfico mostra uma oscilação grande em torno de $0$ enquanto a imagem da função fica limitada entre $-1$ e $1$, como era de se esperar para um seno. Vamos escolher um intervalo $(-a, a)$ qualquer em torno de $0$.
Notamos que, mesmo que $a$ seja bem pequeno, é possível escolher algum valor de $n$ com $1/n <a$. Em especial, $1/(n\pi) < a$. Ao avaliar a função nesse valor de $x$ teremos $\mathrm{sen}(n\pi) = 0$. Portanto em qualquer intervalo em torno de $0$, existem valores de $x$, tais que $f(x) = 0$.
Por outro lado, se escolhermos $n$ tal que $x = \frac{1}{\pi(1 + 4n)} < a$, teremos $1/x = \pi/2 + 2n\pi$ e quando calcularmos $f(x)$ o resultado será $1$. Então, quando nos aproximamos de $0$, sempre haverá pontos com $f(x) = 0$ e pontos com $f(x) = 1$. Conclusão: não existem os limites laterais no $0$, portanto o limite $\displaystyle \lim_{x \rightarrow 0} \mathrm{sen} \left(\frac{1}{x}\right)$ não existe!
O interesse maior nesse caso, como mostrado no vídeo, é que temos uma função limitada, que não possui nenhum dos limites laterais no $0$, multiplicada por uma outra ($g(x)=x$) que está tendendo a zero. Nesse caso, o limite do produto existe e é zero! Esse fato é consequência do seguinte resultado:
(Anulamento) Seja $g(x)$ uma função limitada em algum intervalo em torno de $a$, exceto, possivelmente, no próprio $a$, ou seja, $|g(x)|\leq M, \forall x \in (a-r,a)\cup (a,a+r)$,para algum $r>0$. Se $\displaystyle \lim_{x\rightarrow a} f(x) =0$, então $\displaystyle \lim_{x \rightarrow a} f(x)g (x) = 0$.
O Teorema do Anulamento nos diz que se tomarmos uma função limitada e fizermos o produto por uma função que tende a $0$, então esse produto tem limite $0$. No caso das funções seno e cosseno, elas são limitadas em toda a reta, ou seja $|\mathrm{sen}(x)|\leq1$ e $|\cos(x)|\leq1$, $\forall x \in \mathbb{R}$.
Calcular $\displaystyle \lim_{x\,\rightarrow 0}\mathrm{sen}(x)\cos(1/x^2)$.
Nesse caso, temos
$\mathrm{sen}(x) \rightarrow 0$, quando $x\rightarrow 0$ e $|\cos(1/x^2)|\leq1, \forall x \neq0$.
Portanto, pelo Teorema do Anulamento, segue que $\displaystyle \lim_{x\,\rightarrow 0}\mathrm{sen}(x)\cos(1/x^2)=0$. Note que a função $y=\cos(1/x^2)$ não possui limite em $x=0$, já que a medida em que nos aproximamos de $0$, $1/x^2$ cresce de maneira ilimitada, fazendo o cosseno oscilar entre -1 e 1, indefinidamente.