
Atenção! Não leia esse tópico antes de ver o vídeo Olhando o infinito, (clicando na caixa abaixo), e estudar a Seção 1, sobre a definição formal de limite. Não são assuntos interdependentes, porém essa parte estende e referencia algumas noções, exemplos e conceitos discutidos lá.
Até o momento, estudamos sobre o limite quando $x$ tendia a um valor determinado $a$. Esse limite, se existisse, seria também um número real bem definido $L$. Aqui, vamos estender essa ideia, pensando no ``infinito''.
As Figuras ??? e ??? ilustram exemplos de comportamentos que podemos identificar como alvos desse estudo. No caso da primeira figura, observamos que se $x$ fica muito grande tanto no sentido positivo quanto no negativo, ou seja, muito grande em módulo, a imagem da função se aproxima de uma constante, como indicado pela reta em vermelho. Na segunda figura, se $x$ tende a $3$, a imagem da função fica muito grande. Acontece que ``muito grande'' é uma expressão vaga, que depende de interpretação. Queremos entender melhor isso, explicitando o sentido de alguma grandeza real tender a infinito ou a menos infinito.
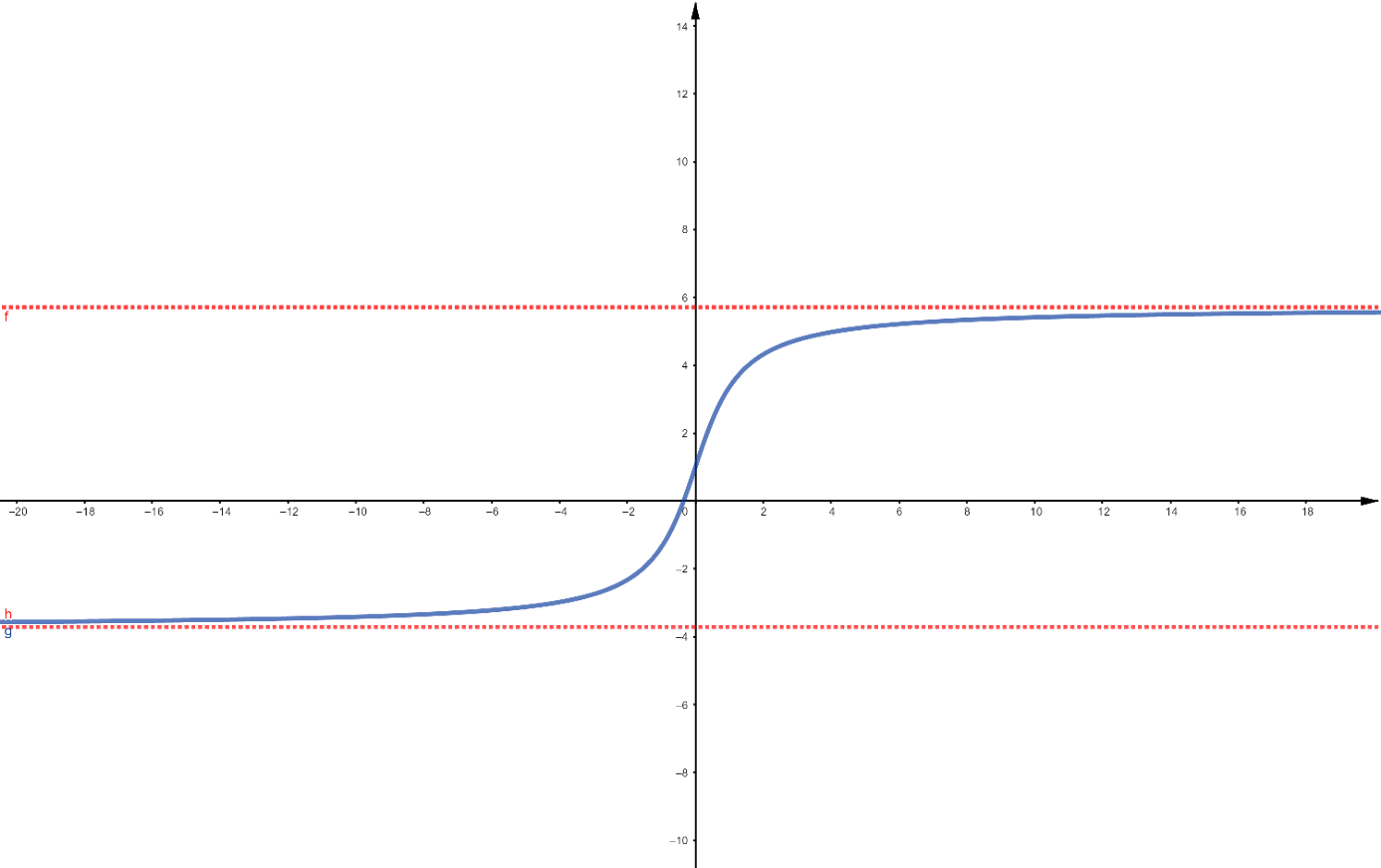
Figura 1: Quando $x$ tende a mais ou menos infinito,
$f(x)$ tende a uma constante.
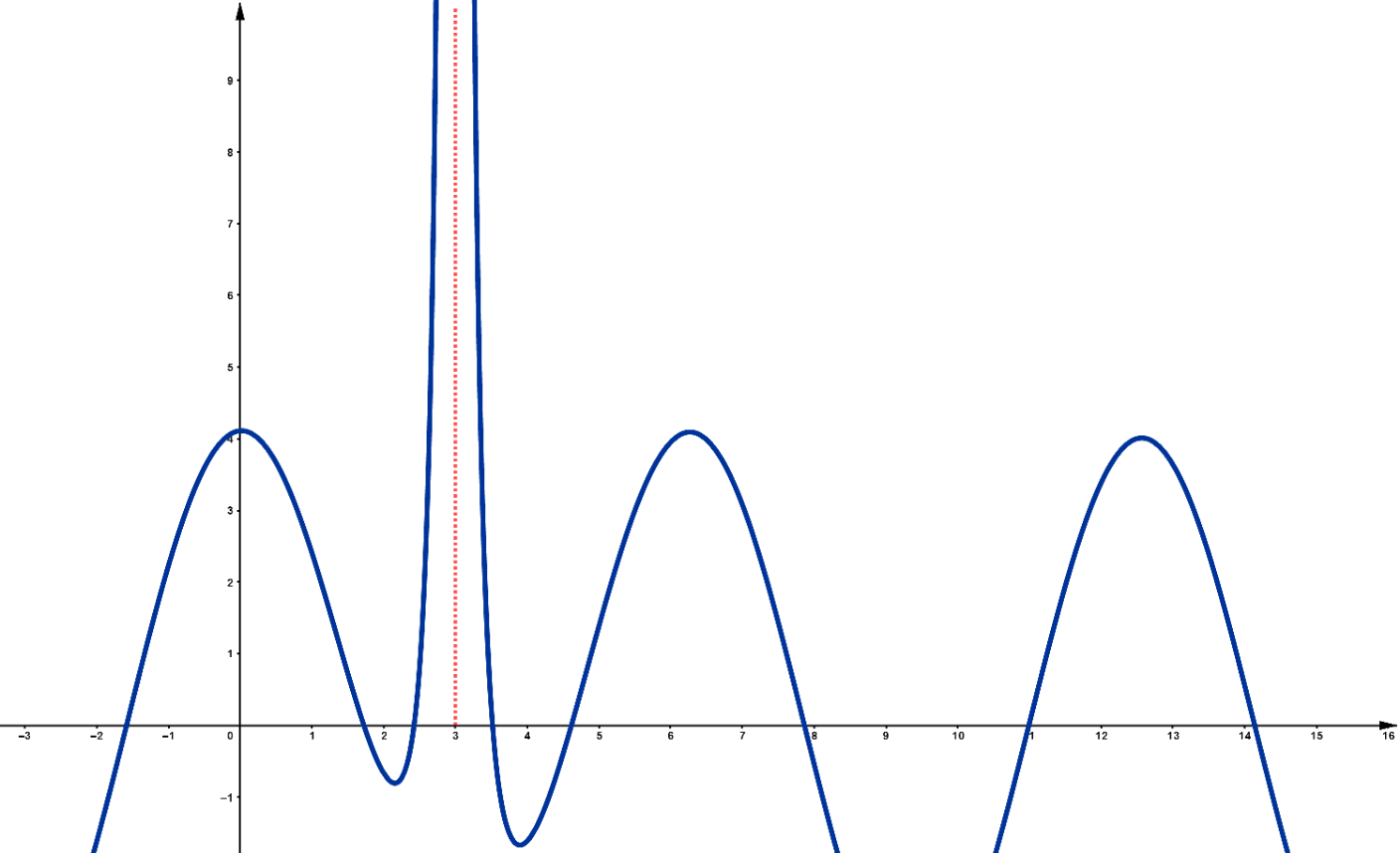
Figura 2: Quando $x\rightarrow 3$, $f(x)$ tende a infinito.
Dizemos que alguma grandeza variável $G$ em $\mathbb{R}$, tende a infinito ($\infty$ ou $+\infty$) quando, para todo número $M > 0$, a partir de algum momento tenhamos $G > M$. Isto é, não importa o quanto o número $M$ escolhido seja grande, a partir de algum instante, a grandeza $G$ se torna maior do que $M$ e assim permanece.
Dizemos que alguma grandeza $G$ em $\mathbb{R}$, tende a menos infinito ($-\infty$) quando, para todo número $M < 0$, a partir de algum momento, $G < M$. Isto é, não importa o quanto o número $M$ escolhido seja grande no sentido negativo, a partir de algum momento, a grandeza $G$ se torna menor do que $M$ e assim permanece.
Destacamos aqui que ``infinito'' não é um número muito grande!!! Quando dizemos, por exemplo, que $x$ tende a infinito ou $f(x)$ tende a infinito, não estamos usando o conceito de limite definido anteriormente. Ao contrário, se $x$ tende a infinito, é porque $x$ não está se aproximando de número algum, mas crescendo muito e superando definitvamente qualquer número real $M$. Portanto, o limite tal como foi definido na semana anterior não existe. Nesse tópico, vamos subdividir o estudo em duas partes. Na primeira, a variável do domínio tende a $\infty$ ou $-\infty$ ($x \rightarrow \infty$ ou $x\rightarrow -\infty$). Na segunda, a imagem da função tende a infinito ($f(x) \rightarrow \infty \text{ ou }-\infty$).
No tópico anterior, vimos o problema da pessoa que caminha de um ponto a outro. Ela caminha com uma regra determinada: a cada tempo, só pode caminhar metade da distância que falta para o ponto de chegada. O resultado, como discutido, é que ela se aproxima arbitrariamente do ponto de chegada. Mas nunca o atinge, mesmo não parando de caminhar. Lembramos da função $P(t)$, definida ali, e dizemos que o limite quanto $t$ tende a infinito de $P(t)$ é $B$ (ponto de chegada) ($\displaystyle \lim_{t \rightarrow \infty}P(t) = B)$.
Conceitualmente, esse não é exatamente o mesmo tipo de estudo que discutimos na semana anterior. O fato de $t$ não se aproximar de um valor determinado, mas crescer indefinidamente, faz com que o problema tenha que ser redefinido. A definição antes apresentada se modifica para:
Intuitivamente, diremos que o limite quando $x$ tende a infinito de uma função $f(x)$ existe e é igual a $L$, um número real, se a distância entre $f(x)$ e $L$ se tornar arbitrariamente pequena para $x$ suficientemente grande.
Denotaremos isto escrevendo
\[\lim_{x\to\infty} f(x) = L.\]Em matematiquês puro, a definição fica:
(Limite no Infinito)
Dizemos que $\displaystyle\lim_{x \rightarrow \infty} f(x) = l$ se, e somente se, para todo $\varepsilon >0$, existe $M$, tal que se $x>M$, $|f(x) -l| < \varepsilon$.
Tente estabelecer uma relação entre a definição 1 e a definição de limite apresentada no último tópico. O que existe de parecido? E de diferente? procure generalizar a definição para o caso em que $x$ tende a menos infinito. Sob o ponto de vista computacional, em um primeiro momento, a ideia é raciocinar com a intuição, com a ajuda de gráficos e/ou tabelas.
Considere $f(x) = \displaystyle\frac{1}{x^r}$, $x \neq 0$. Se $r \in \mathbb{R}$ e $r>0$ então:
\[\displaystyle \lim_{x \rightarrow \infty} f(x) = 0\]Note que se $r>0$ então, quando $x\rightarrow \infty$, $x^r $ cresce cada vez mais. Temos portanto um número fixo sendo dividido por valores cada vez maiores o que, evidentemente, se aproxima de $0$. As figuras ??? e ??? ilustram o resultado.
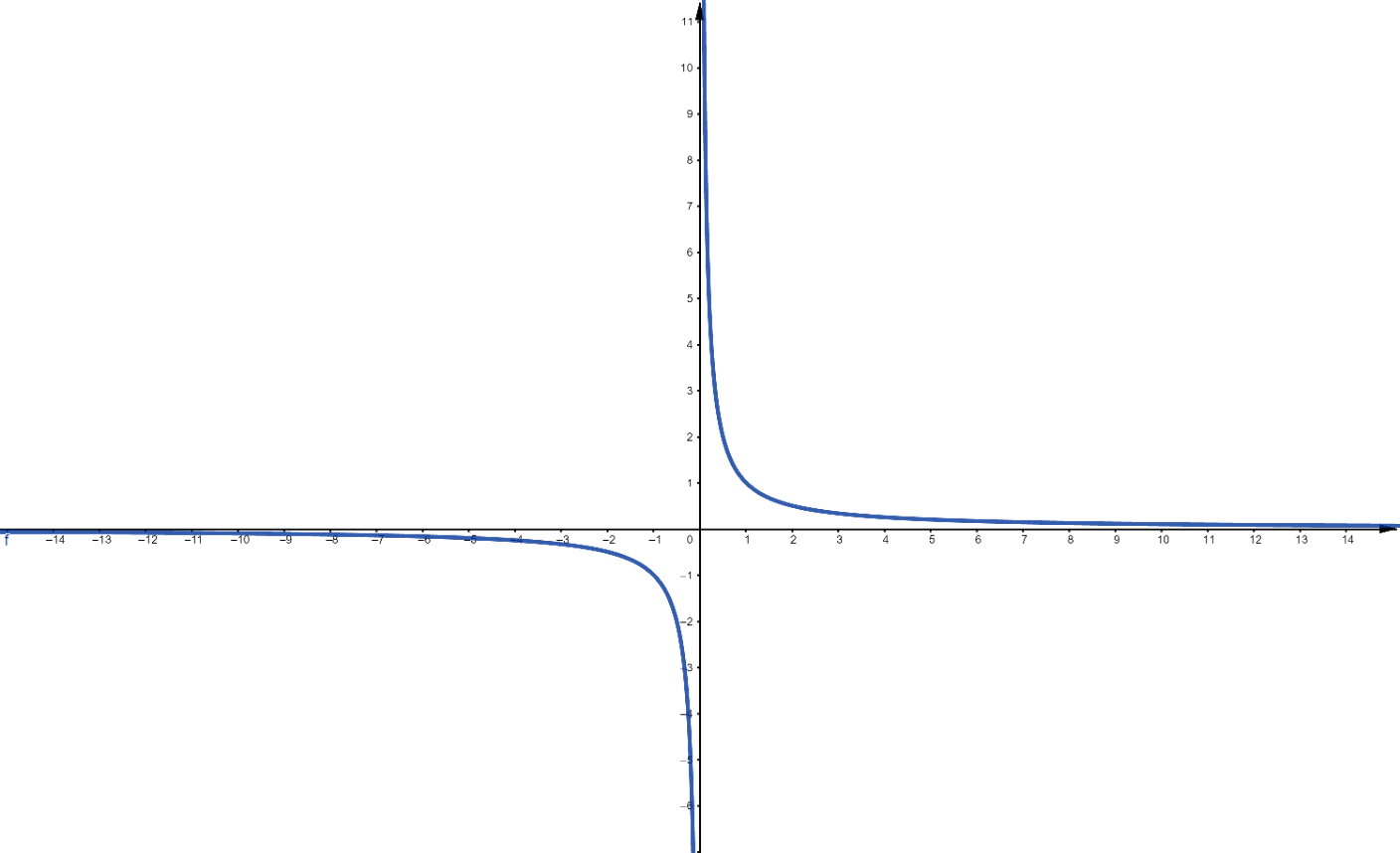
Figura 3: Gráfico de $f(x)=\frac{1}{x}$.
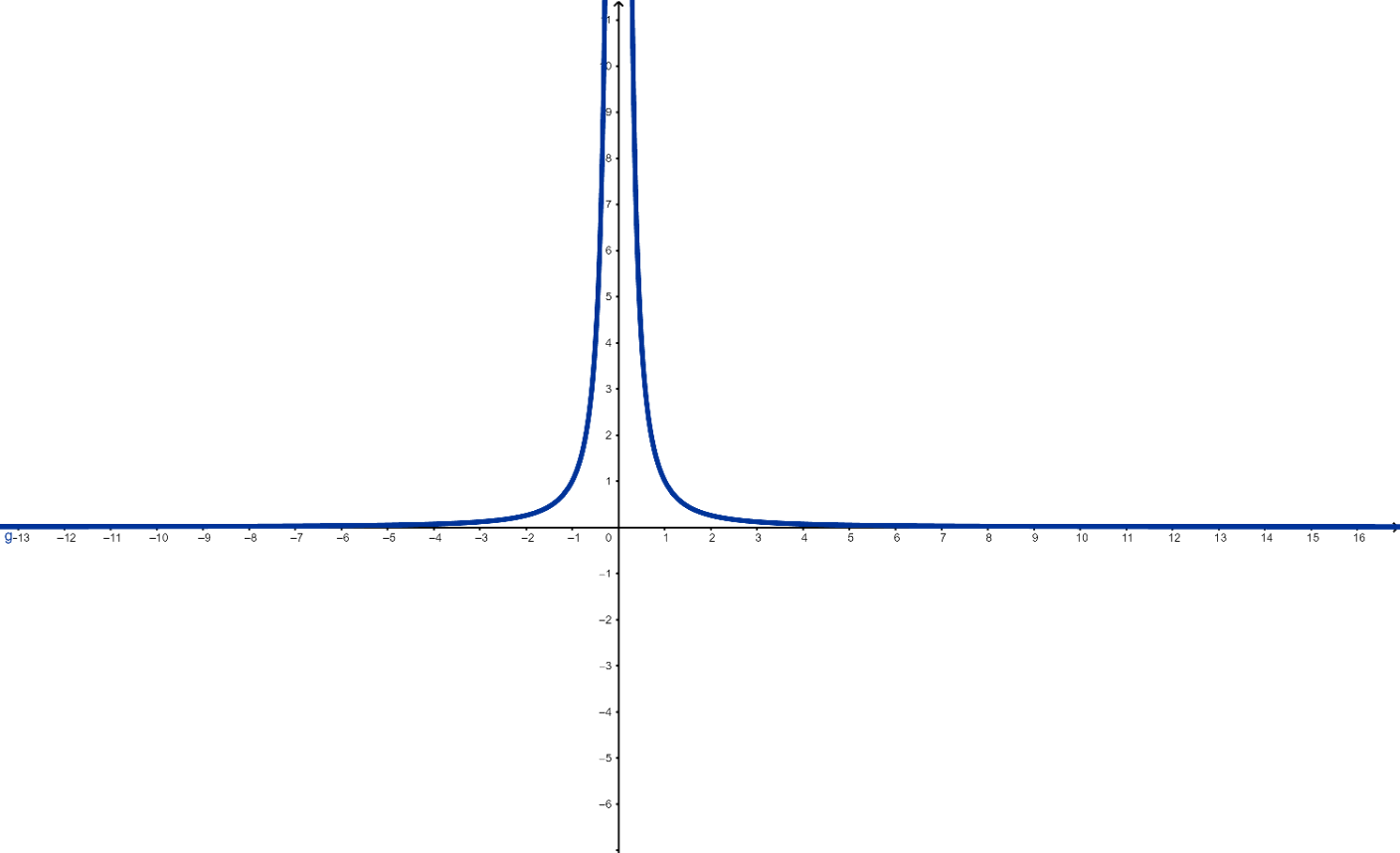
Figura 4: Gráfico de $f(x)=\frac{1}{x^2}$.
Vale notar que, se $x \rightarrow -\infty$, $f(x)$ também tende a $0$, se o expoente $r$ for tal que $x^r$ é definido. Por exemplo, se $r= 1/2$, só podemos definir $1/x^r$ para valores positivos, de modo que não faria sentido estudar o limite em menos infinito.
No estudo do limite, quando $x$ tende a infinito, de funções mais simples (como polinômios, exponenciais, funçãos trigonométricas em geral) a intuição costuma ser suficiente. Todavia, quando lidamos com produtos ou quocientes podem surgir alguns problemas.
$f(x) = \displaystyle \frac{4x^3 +x}{x^3-1}$, $x \in \mathbb{R}$, $x \neq 1$. Nesse caso, temos uma fração em que numerador e denominador crescem muito, quando $x \rightarrow \infty$. Uma maneira de analisar é dividir cada termo pelo monômio de maior grau no denominador (no caso $x^3$).
\[f(x) =\displaystyle \dfrac{\dfrac{4x^3}{x^3} + \dfrac{x}{x^3}}{\dfrac{x^3}{x^3} - \dfrac{1}{x^3}} \; \; \mbox{se } x \neq 0\]observe que essa divisão não pode ser feita em $x=0$, mas isso não importa porque queremos estudar o limite no infinito (bem longe de $0$). Como $\frac{x}{x^3}=\frac{1}{x^2}$ e $\frac{1}{x^3}$ tendem a $0$ quando $x \rightarrow \infty$, temos
Esta situação é um exemplo de indeterminação do tipo $[\infty / \infty]$, que será visto com mais detalhes na Seção ???. Note que, ao escervermos $[\infty / \infty]$, não estamos dividindo, é apenas uma notação para indicar a indeterminação.

Figura 5: $\displaystyle\lim_{x\to\infty} \frac{4x^3 +x}{x^3-1} =4$
Um segundo exemplo interessante é $\displaystyle\lim_{x \rightarrow \infty} \displaystyle\frac{\cos(x)}{x}$. Observe que o numerador varia entre $-1$ e $1$. essencialmente, estamos dividindo um valor limitado por alguma coisa que está crescendo indefinidamente. A consequência é que a fração fica cada vez menor, se aproximando de $0$, que é o valor do limite.
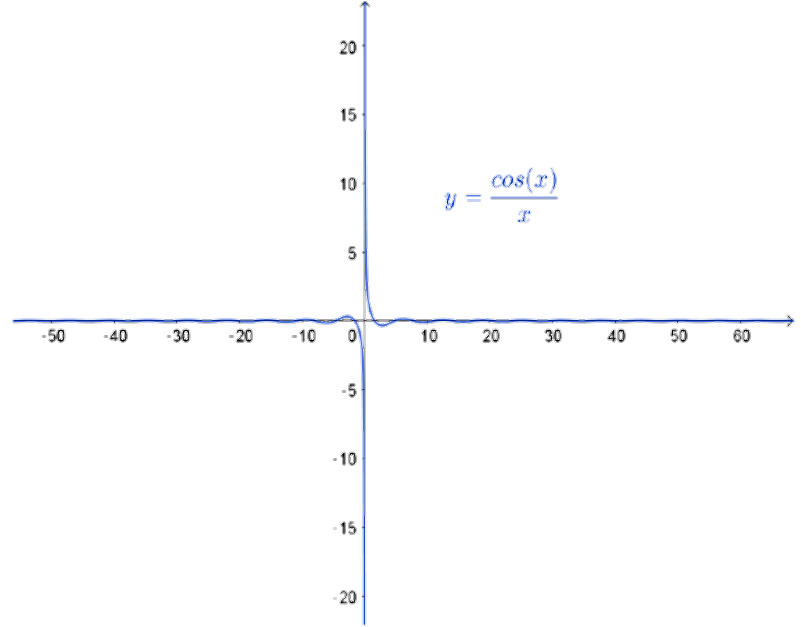
Figura 6: $\displaystyle\lim_{x\to\infty} \displaystyle\frac{\cos(x)}{x} =0$
Este exemplo ilustra como o Teorema do Anulamento, estudado na semana passada, continua valendo quando $x\to \infty$. Neste caso, temos a função limitada $\cos(x)$ sendo multiplicada pela função $1/x$, que tende a 0 quando $x\to\infty$.
Observe o gráfico de $1/x$ na Figura ???. Tanto em $\infty$ quanto em $-\infty$, a função tende a zero. Entretanto há uma diferença na ``maneira'' com que $1/x$ se aproxima de $0$, quando analisamos os casos $-\infty$ e $\infty$. Em infinito, $f(x)$ se aproxima de $0$ só por valores positivos. Nesse caso, é comum escrever: $\displaystyle\lim_{x\rightarrow \infty} \frac{1}{x} = 0^+$ e o sinal de $+$ no $0$ é colocado justo para indicar que a aproximação só ocorre por valores positivos. Analogamente, se $x$ tende a menos infinito, pode-se escrever $\displaystyle\lim_{x\rightarrow -\infty} \frac{1}{x} = 0^-$ indicando que, nesse caso, $f(x)$ se aproxima de $0$ por valores negativos. No entanto, o gráfico de $y=\dfrac{\cos(x)}{x}$ tende a zero oscilando entre valores positivos e negativos, por conta da oscilação do cosseno.
Considere $\displaystyle \lim_{x \rightarrow \infty} \sqrt{x^2 -5} -x $.
Analisando esse limite, vemos que $\sqrt{x^2 -5}$ e $x$ crescem muito quando $x$ cresce muito, porém temos uma diferença entre eles e não sabemos o que vai ocorrer. Então, estamos diante de uma nova indeterminação do tipo $[\infty-\infty]$, pois não sabemos determinar o limite com a função escrita desta forma (nem mesmo sabemos se existe o limite!). Um recurso possível aqui é multiplicar e dividir a função pelo conjugado $\sqrt{x^2 -5} +x$ para tentar analisar o que acontece sem a raiz quadrada no numerador. Temos:
E temos um número dividido por algo que cresce indefinitamente (observe que $\sqrt{x^2 -5} +x$ não é indeterminado, é a soma de duas funções que crescem indefinidamente, possuem o mesmo sinal!). Portanto, o limite vale $0$.
Sob o ponto de vista gráfico, conforme discutido no vídeo, os limites no infinito, quando existem, dão origem às retas horizontais chamadas de assíntotas horizontais. Veremos mais detalhes sobre assíntotas na Seção ???.
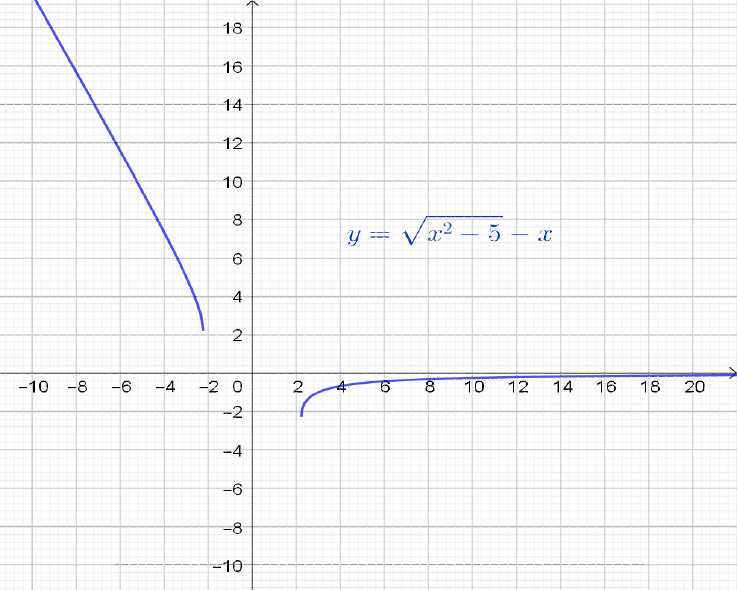
Figura 7: $\displaystyle \lim_{x \rightarrow \infty} \sqrt{x^2-5}-x=0$.
Observação: As propriedades de operação com limites de funções (que são números reais!), que vimos quando $x\to a$, continuam valendo para $x \to \pm \infty$. O Teorema do Anulamento também vale, com as devidas adaptações no enunciado.
$\displaystyle\lim_{x\to+\infty} \cos\left(\frac{1}{x}\right)$
Nesse caso, $1/x$ tende a zero , quando $x\to \infty$, portanto $\displaystyle \lim_{x\to+\infty} \cos\left(\frac{1}{x}\right)=1.$
$\displaystyle \lim_{x\to+\infty} x \ \mathrm{sen}\left(\frac{1}{x}\right)$
Nesse caso, $\displaystyle \lim_{x\to+\infty} \mathrm{sen}\left(\frac{1}{x}\right)=0$ e $x$ tende a $+\infty$, isso é outro tipo de indeterminação $[0\cdot \infty]$! Ou seja, não sabemos o que acontecerá com esse limite, a menos que façamos algum tipo de manipulação com a função. Assim, vamos trocar a variável, escrevendo $u=\left(\frac{1}{x}\right)$, onde $u \to 0^+$, pois $x \to \infty$. Logo,
$\displaystyle \lim_{x\to+\infty} x \, \mathrm{sen}\left(\frac{1}{x}\right)= \displaystyle \lim_{u\to 0^+} \dfrac{\mathrm{sen}(u)}{u}=1$ (Limite trigonométrico Fundamental).
Note que não podemos usar o Teorema do Anulamento, pois $y=x$ não é limitada para $x\to \infty.$
Uma segunda questão a ser analisada é que em determinadas circunstâncias, a imagem de uma função pode tender a infinito ou a menos infinito. Mais uma vez, o gráfico de $y = \displaystyle\frac{1}{x}$ é uma boa referência. Quando $x$ tende a $0^-$, $f(x)$ tende a menos infinito e quando $x$ tende a $0^+$, $f(x)$ tende a infinito.
De um modo geral, números ou funções limitadas divididas por ``alguma coisa’’ que tende a zero, tendem a infinito.
A razão pode ser percebida, por exemplo, na tabela em que $a$ é um número real diferente de $0$ sendo dividido $a$ por valores cada vez mais próximos de $0$.
| ${x \rightarrow 0^-}$ | $ {x \rightarrow 0^+} $ | ||
| $ \;\;\; x$ | $a/x$ | $\;\;\; x$ | $a/x$ |
| $-1/2$ | $-2a$ | $1/2$ | $2a$ |
| $-1/4$ | $-4a$ | $1/4$ | $4a$ |
| $-1/{10}$ | $-10a$ | ${1}/{10}$ | $10a$ |
| $-{1}/{500}$ | $-500a$ | ${1}/{500}$ | $500a$ |
| $-{1}/{10^5}$ | $-10^5 a$ | ${1}/{10^5}$ | $10^5 a$ |
A Figura ??? exibe o gráfico de $f(x) = \sec(x)$ que tende a $\infty$ em infinitos valores. Esse comportamento é consequência do fato do cosseno se anular em infinitos valores.
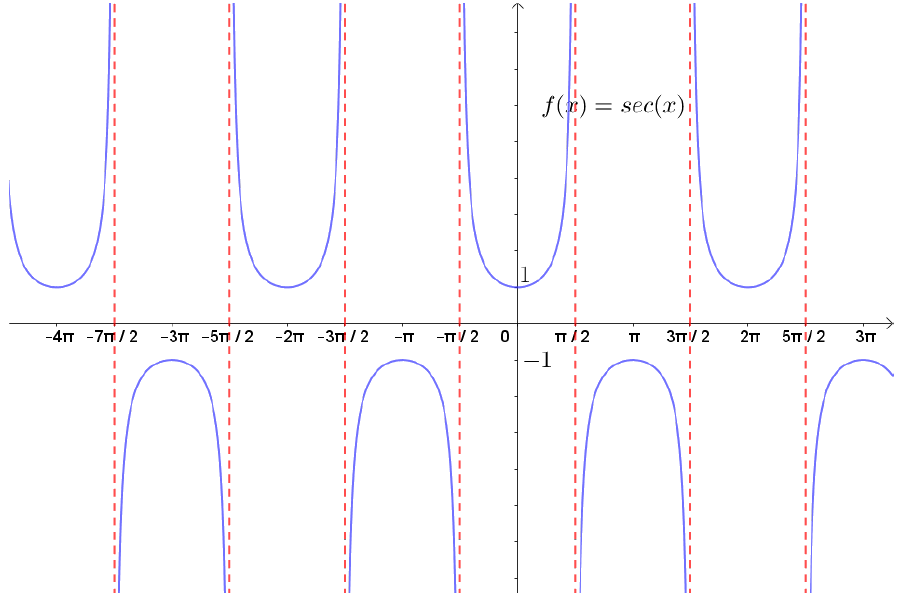
Figura 8: Gráfico de $f(x) = \sec(x)$.
Lembrando que $\sec(x)=\frac{1}{\cos(x)}$, sempre que $x\to \frac{\pi}{2} + k\pi$, com $k\in\mathbb{Z}$, o valor de $\cos(x)$ tenderá a 0, o que fará com que $\sec(x)\to \infty$ ou $\sec(x)\to-\infty$, dependendo se $\cos(x)\to 0^-$ ou $\cos(x)\to 0^+$.
Quando uma função tende a infinito a medida em que $x$ tende a um número finito $a$, pela esquerda ou pela direita, a reta $x = a$ é chamada assíntota vertical. Veremos mais exemplos na Seção ???.
Podemos lidar com operações entre funções com limites infinitos, ou que resultem em limites infinitos, de forma bem intuitiva, desde que tomando os cuidados com as indeterminações que veremos na próxima seção.
Denotaremos por $\pm\infty$ algo que possa ser lido tanto com $+\infty$ quanto com $-\infty$, ou que possa assumir apenas um dos casos, dependendo de uma análise mais cuidadosa de sinais.
Podemos então enunciar as seguintes propriedades:
Propriedades:
Estes resultados continuam válidos quando trocamos $x\to a$ por $x\to a^-$, $x\to a^+$, $x\to \infty$ ou $x\to -\infty$.
$\displaystyle\lim_{x\to 1}\;\frac{e^x}{\left|1-x^3\right|}$.
Quando $x\to 1$, temos $e^x\to e$, $\left|1-x^3\right|\to 0^+$ (note que há um módulo).
Assim, $\displaystyle\lim_{x\to 1}\;\frac{e^x}{\left|1-x^3\right|} = +\infty$.
$\displaystyle\lim_{x\to 1}\;\frac{x}{x^2-1}$.
Podemos ver que o numerador tende a $1$ e o denominador a $0$. Assim, teremos limite $+\infty$ ou $-\infty$ e precisamos avaliar com cuidado os sinais. Com $x$ próximo de 1, o numerador $x$ será positivo. O denominador $x^2-1$ é uma expressão quadrática de raízes $-1$ e $1$, portanto é negativa quando $x\to 1^-$ e positiva quando $x\to 1^+$. Assim,
\[\lim_{x\to 1^-}\frac{x}{x^2-1} = -\infty,\] \[\lim_{x\to 1^+}\frac{x}{x^2-1} = +\infty.\]$\displaystyle\lim_{x\to 0^+}\ln(x)\cdot \cos(x)$. Quando $x\to 0^+$, temos $\ln(x)\to - \infty$ e $\cos(x)\to 1$. assim, $\displaystyle\lim_{x\to 0^+}\ln(x)\cdot \cos(x) = -\infty$.
Já foi mencionado que, quando uma função tende a infinito quando $x$ tende a um número finito $a$, pela esquerda ou pela direita, a reta $x = a$ é chamada assíntota vertical.
Isto signifca que o valor da função ``explodirá’’ quando $x$ se aproximar de $a$, como nos exemplos abaixo:
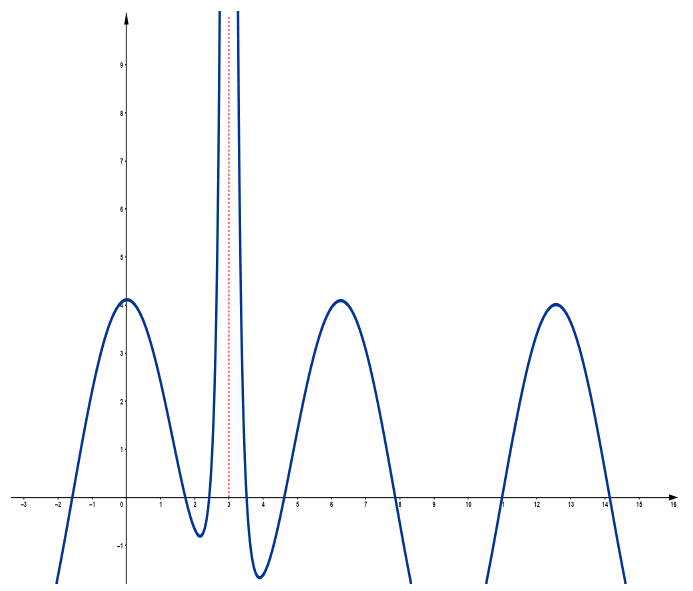
Figura 9: Quando $x\rightarrow 3$, $f(x)$ tende a $\infty$ ;
$ x=3$ é assíntota vertical.

Figura 10: Quando $x\rightarrow 1^+$, $f(x)$ tende a $-\infty$;
$x=1$ é assíntota vertical.
De maneira mais precisa, definimos:
(Assíntotas verticais) A reta $x=a$ é uma assíntota vertical do gráfico da função $f$ se pelo menos um dos limites abaixo vale:
\[\lim_{x\to a^-}f(x) = \infty, \lim_{x\to a^-}f(x) = -\infty, \lim_{x\to a^+}f(x) = \infty, \lim_{x\to a^+}f(x) = -\infty.\]É claro que, se $\displaystyle\lim_{x\to a^-}f(x) = \infty$ ou $\displaystyle\lim_{x\to a^-}f(x) = -\infty$, duas das condições acima (à esquerda e à direita) serão satisfeitas, logo teremos assíntota $x=a$.
$f(x)=\frac{1}{x^2-3x+2}$, $x\neq 1,2.$

Figura 11: Quando $x\rightarrow 1^- (\text{ou} \ 2^+)$, $f(x)$ tende a $\infty$ ;
$ x=1$ e $x=2$ são assíntotas verticais.
Se a reta $x=a$ é uma assíntota da função $f$, não necessariamente o ponto $a$ estará fora do domínio da função $f$. Veja, por exemplo, o gráfico da figura 11, onde $x=1$ é assíntota vertical e $1\in \mathrm{D}(f)$.
(Assíntotas horizontais) A reta $y=L$ é uma assíntota horizontal do gráfico da função $f$ se $\displaystyle\lim_{x\to\infty}f(x)=L$ ou $\displaystyle\lim_{x\to -\infty}f(x)=L$.
No Exemplo 11, vemos que o gráfico possui uma assíntota horizontal, que é a reta $y=0$. Em geral, um gráfico de uma função pode ter no máximo duas assíntotas horizontais distintas, uma para $+\infty$ e outra para $-\infty$. Porém, pode ter uma infinidade de assíntotas verticais, como acontece com os gráficos da tangente, secante, cotangente e cossecante.
Determine as assíntotas do gráfico da função $f(x)=\dfrac{x^2}{x^2-1}$ e encontre seu domínio.
Observe que $\mathrm{D}(f)=\mathbb{R}-\{\pm1\}$ . Vamos ver se existe alguma assíntota horizontal :
$\displaystyle\lim_{x\to -\infty}\dfrac{x^2}{x^2-1}=\displaystyle\lim_{x\to -\infty}\dfrac{1}{1-\frac{1}{x^2}}=1$ e de forma análoga, $\displaystyle\lim_{x\to \infty}\dfrac{x^2}{x^2-1}=\displaystyle\lim_{x\to \infty}\dfrac{1}{1-\frac{1}{x^2}}= 1$.
Assim, há uma única assíntota horizontal, que é a reta $y=1$.
Os únicos valores de $x$ onde há a possibilidade de encontrarmos assíntotas verticais são $x=1$ e $x=-1$, que são pontos fora do domínio, mas onde podemos calcular limite da $f$, pois podemos nos aproximar deles ``sem sair do domínio’’ da $f$. Esses valores são candidatos a assíntotas verticais, mas devemos checar!
$\displaystyle\lim_{x\to -1^-}\dfrac{x^2}{x^2-1}=+\infty$, logo $x=-1$ será uma assíntota vertical.
Você poderá fazer os outros limites laterais, mas esses dois bastam para afirmarmos que $x=1$ e $x=-1$ são assíntotas verticais.
Vale a pena pensar qual seria a interpretação da presença de uma assíntota em algum gráfico de uma função que representasse algum problema. Isso vai depender do problema (discutimos alguns casos no vídeo). Se a função descreve velocidade do vento, uma assíntota vertical pode significar perigo. Se descreve o comportamento da ação que você comprou na bolsa de valores, uma assíntota vertical pode significar que você vai ficar rico. Uma assíntota horizontal, em um gráfico que descreve temperatura no tempo, por exemplo, indica que houve uma estabilização.
Nas Propriedades 7, vimos algumas regras de operação com limites infinitos. Nestas regras, era bastante intuitivo entender (e acreditar) o que se passava; de alguma forma, os infinitos envolvidos estavam ``em uma mesma direção’’, como por exemplo a soma de dois limites $+\infty$ ou de dois limites $-\infty$, ou o produto de dois limites infinitos.
Um problema frequente aparece quando analisamos expressões que envolvem quocientes onde numerador e denominador tendem a $\infty$ ou a $0$ (que é a mesma coisa, basta trocar $f$ por $1/f$. Coisas como exponenciais sobre polinômios, ou mesmo quociente de polinômios onde o denominador se anula, exigem cuidado. Também teremos problema ao analisarmos uma expressão que tende a 0 multiplicando outra que tende a $\infty$, ou diferença entre expressões que tendem, ambas, a um $\infty$ com mesmo sinal.
Estas situações não possuem uma regra geral como as que vimos, e devem ser analisadas caso a caso. São as chamadas indeterminações.
Indeterminação $[\infty/\infty]$:
Suponha que $f(x) \to +\infty$ e $ g(x) \to +\infty$, não podemos afirmar nada sobre $\displaystyle\lim \frac{f(x)}{g(x)}$. Veja alguns exemplos:
\[\lim_{x\to \infty} \frac{x^2}{x} = \lim_{x\to \infty} x = + \infty\] \[\lim_{x\to \infty} \frac{x}{x^2} = \lim_{x\to \infty} \frac{1}{x} = 0\] \[\lim_{x\to \infty} \frac{2x}{x} = \lim_{x\to \infty} 2 = 2\]Em todos os casos, numerador e denominador tendem a $+\infty$.
O Exemplo 2 lida com esta indeterminação. Os Exemplos ???, ??? e ???, abaixo, ampliam a discussão do Exemplo 2.
Indeterminação $[\infty - \infty]$:
Suponha que $f(x) \to +\infty$ e $ g(x) \to +\infty$, não podemos afirmar nada sobre $\displaystyle \left(f(x)-g(x)\right)$.
\[\lim_{x\to \infty} \left( x^2-x\right) = \lim_{x\to \infty} x^2\left(\vphantom{\frac{1}{x}}\right.1-\cancelto{0}{\frac{1}{x}}\left.\vphantom{\frac{1}{x}}\right) = + \infty\] \[\lim_{x\to \infty} \left( x-x^2\right) = \lim_{x\to \infty} x^2\left(\vphantom{\frac{1}{x}}\right. \cancelto{0}{\frac{1}{x}} - 1\left.\vphantom{\frac{1}{x}}\right) = - \infty\] \[\lim_{x\to \infty} \left((x+1)-x\right) = \lim_{x\to \infty} 1 = 1\]Em todos os casos, as duas parcelas da subtração tendem a $+\infty$.
O Exemplo 4 lida com esta indeterminação.
Indeterminação $[0 \cdot \infty]$:
Suponha que $ f(x) \to 0$ e $g(x) \to +\infty$, não podemos afirmar nada sobre $\displaystyle \left(f(x)\cdot g(x)\right)$. Veja alguns exemplos:
\[\lim_{x\to 0^+} x^2\cdot \frac{1}{x} = \lim_{x\to 0^+} x = 0\] \[\lim_{x\to 0^+} x\cdot \frac{1}{x^2} = \lim_{x\to 0^+} \frac{1}{x} = +\infty\] \[\lim_{x\to \infty} \frac{1}{x}\cdot x = \lim_{x\to \infty} 1 = 1\]O Exemplo 6 lida com esta indeterminação.
Indeterminação $[0/0]$:
Este tipo de indeterminação foi muito visto na semana anterior, no caso em que $x\to a$. Se $ f(x) \to 0$ e $ g(x) \to 0$, nada pode ser dito sobre o limite do quociente $\frac{f(x)}{g(x)}$. Exemplos:
\[\lim_{x\to 0} \frac{x^2}{x} = \lim_{x\to 0} x = 0\] \[\lim_{x\to 0} \frac{x}{x^3} = \lim_{x\to 0} \frac{1}{x^2} = +\infty\] \[\lim_{x\to 0} \frac{2x}{x} = \lim_{x\to 0} 2 = 2\] \[\lim_{x\to 0} \frac{x}{x^2} = \lim_{x\to 0} \frac{1}{x}\;, \textnormal{que não existe}\]Note que $[\infty/\infty]$, $[\infty-\infty]$, $[0\cdot \infty]$ e $[0/0]$ não denotam divisão, subtração ou produto, são apenas formas de representarmos o comportamento ou tendência das funções envolvidas. Estas funções não são iguais a 0 ou $\infty$, elas apenas tendem a 0 ou a $\infty$.
Nas Propriedades 7, vimos que não são indeterminações: $[L/0]$, $[\infty/0]$, $[0/\infty]$, $[L/\infty]$, $[\infty\cdot\infty]$, $[\infty+\infty]$, $[-\infty-\infty]$, $[L+\infty]$ e $[L-\infty]$, onde $L\in\mathbb{R}$ é o limite de uma função.
$\displaystyle\lim_{x\to +\infty} \frac{a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0}$ (razão entre polinômios de mesmo grau,
com $x\to +\infty$
Vamos proceder como no Exemplo 2 e dividir numerador e denominador por $x^n$:
\[\lim_{x\to +\infty} \frac{a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0} = \lim_{x\to +\infty} \frac{\frac{a_nx^n}{x^n} + \frac{a_{n-1}x^{n-1}}{x^n} + ... + \frac{a_1x}{x^n} + \frac{a_0}{x^n}}{\frac{b_nx^n}{x^n} + \frac{b_{n-1}x^{n-1}}{x^n} + ... + \frac{b_1x}{x^n} + \frac{b_0}{x^n}} =\]\[=\lim_{x\to +\infty} \frac{a_n + \cancelto{0}{\frac{a_{n-1}}{x}} + ... + \cancelto{0}{\frac{a_1}{x^{n-1}}} + \cancelto{0}{\frac{a_0}{x^n}}}{b_n + \cancelto{0}{\frac{b_{n-1}}{x}} + ... + \cancelto{0}{\frac{b_1}{x^{n-1}}} + \cancelto{0}{\frac{b_0}{x^n}}} = \frac{a_n}{b_n}.\]
O resultado se mantém para $x\to-\infty$.
$\displaystyle\lim_{x\to +\infty} \frac{a_mx^m + a_{m-1}x^{m-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0}, m > n$ (razão entre polinômios com maior grau no numerador, com $x\to +\infty$
Temos
\[\lim_{x\to +\infty} \frac{a_mx^m + a_{m-1}x^{m-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0} = \lim_{x\to +\infty} \frac{x^m \left(\frac{a_mx^m}{x^m} + \frac{a_{m-1}x^{m-1}}{x^m} + ... + \frac{a_1x}{x^m} + \frac{a_0}{x^m}\right)}{x^n\left(\frac{b_nx^n}{x^n} + \frac{b_{n-1}x^{n-1}}{x^n} + ... + \frac{b_1x}{x^n} + \frac{b_0}{x^n}\right)} =\]\[=\lim_{x\to +\infty} \frac{x^{m-n}\left(a_m + \cancelto{0}{\frac{a_{m-1}}{x}} + ... + \cancelto{0}{\frac{a_1}{x^{m-1}}} + \cancelto{0}{\frac{a_0}{x^m}}\right)}{b_n + \cancelto{0}{\frac{b_{n-1}}{x}} + ... + \cancelto{0}{\frac{b_1}{x^{n-1}}} + \cancelto{0}{\frac{b_0}{x^n}}}.\]
Este limite pode ser $+\infty$ ou $-\infty$, dependendo do sinal de $\frac{a_m}{b_n}$. Para $x\to-\infty$, precisaremos também levar em conta se o expoente $m-n$ deste último limite é par (caso no qual $x^{m-n}\to +\infty$) ou ímpar (caso no qual $x^{m-n}\to -\infty$).
$\displaystyle\lim_{x\to +\infty} \frac{a_mx^m + a_{m-1}x^{m-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0}, m < n$ (razão entre polinômios com maior grau no denominador, com $x\to +\infty$
Temos
\[\lim_{x\to +\infty} \frac{a_mx^m + a_{m-1}x^{m-1} + ... + a_1x + a_0}{b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0} = \lim_{x\to +\infty} \frac{x^m \left(\frac{a_mx^m}{x^m} + \frac{a_{m-1}x^{m-1}}{x^m} + ... + \frac{a_1x}{x^m} + \frac{a_0}{x^m}\right)}{x^n\left(\frac{b_nx^n}{x^n} + \frac{b_{n-1}x^{n-1}}{x^n} + ... + \frac{b_1x}{x^n} + \frac{b_0}{x^n}\right)} =\]\[=\lim_{x\to +\infty} \frac{a_m + \cancelto{0}{\frac{a_{m-1}}{x}} + ... + \cancelto{0}{\frac{a_1}{x^{m-1}}} + \cancelto{0}{\frac{a_0}{x^m}}}{x^{n-m}\left(b_n + \cancelto{0}{\frac{b_{n-1}}{x}} + ... + \cancelto{0}{\frac{b_1}{x^{n-1}}} + \cancelto{0}{\frac{b_0}{x^n}}\right)} = 0.\]
Não existe receita nem algoritmo para lidar com indeterminações. Teremos sempre que fazer alguma manipulação algébrica (colocando potências da variável em evidências, cancelando termos que se anulem, etc.) e tentar transformar a indeterminação em algum caso em que possamos aplicar as Propriedades 7 ou algum outro resultado, como Teoremas do Anulamento, Confronto, ou o Limite Trigonométrico Fundamental, por exemplo.
Os exemplos vistos mostram alguns algebrismos que podem ser úteis. Ao longo do texto, apresentamos também alguns recursos de cálculo que devem se somar a outros com a prática. Gráficos também podem ajudar bastante.
Existe ainda uma ferramenta que ajuda muito, conhecida como Regra de L'Hospital ou Teorema de L'Hospital, que será estudada mais tarde, mas não é uma solução mágica. O que é preciso é um tanto de prática. Veremos também que há outras indeterminações, como $[0^0]$, $[\infty^0]$ e $[1^\infty]$.