O Teorema do Valor Intermediário é um dos resultados centrais relativos à continuidade. Apesar de suas muitas aplicações e da profundidade de sua conclusão, sua afirmação é bastante intuitiva e tão fácil de entender quanto de acreditar.

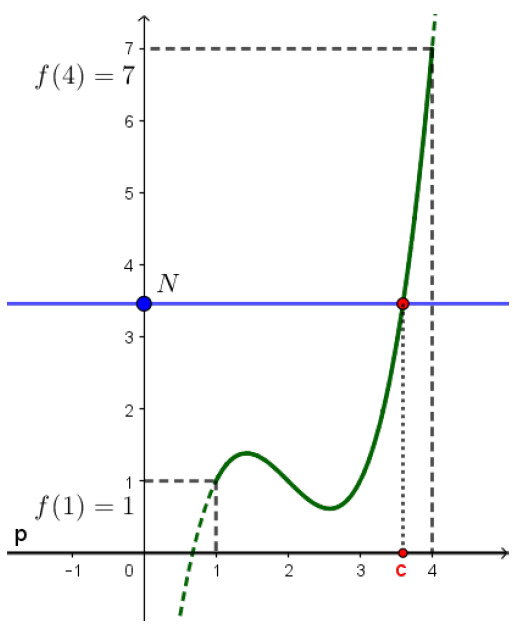
Se $f$ é uma função contínua no intervalo $[a, b]$ , o gráfico da função é desenhado com um único traço unindo os pontos $(a, f (a))$ e $(b, f (b))$ . Vamos supor que $f (a) < f (b)$ , como na figura ao lado.

Considere então qualquer reta horizontal que passe entre os pontos $(a, f (a))$ e $(b, f (b))$ , isto é, qualquer reta $y = N$ , com $f (a) < N < f (b)$ . Esta reta deverá, obviamente, cortar o gráfico da função, pois, como $f$ é contínua no intervalo, seu gráfico não pode saltar de um lado para outro da reta, sem passar por ela. Assim, existirá algum $c \in (a, b)$ tal que $f (c) = N$ .

Obviamente, o resultado continua valendo se $f (a) > f (b) .$

A existência deste $c$ , tal que $f (c) = N$ , dada que a função seja contínua, é o que garante o Teorema do Valor Intermediário (TVI), que enunciaremos a seguir.

Teorema 1

(Teorema do Valor Intermediário) Suponha que $f$ seja contínua em um intervalo fechado $[a, b]$ e seja $N$ um número qualquer entre $f (a)$ e $f (b)$ . Então, existe $c \in (a, b)$ , tal que $f (c) = N$ .

Uma conclusão natural deste resultado, é que, com

x

variando no intervalo

(a, b)

, uma função contínua assume todos os valores entre

f (a)

f (b)

Exemplo 1

Considerando a função definida por $f (x) = x^{3} - 7 x^{2} + 16 x - 11$ , existe algum $c \in (1, 4)$ , tal que $f (c) = 1$ ?

Solução

Sim, pois a $f$ é contínua no intervalo fechado $[1, 4]$ , $f (1) = - 1$ , $f (4) = 5$ e $- 1 < 1 < 5$ , logo o TVI garante que exista tal $c$ . Observe que o TVI não nos diz como encontrar o valor de $c$ (por curiosidade, existem dois valores, $c = 2$ e $c = 3$ ).

Exemplo 2

Considerando a função definida por $f (x) = \frac{1}{x^{2} + 1}$ , existe $c \in (0, + \infty)$ , tal que $f (c) = \frac{1}{π}$ ?

Solução

O TVI não foi enunciado para intervalos ilimitados, como este, portanto não podemos utilizá-lo diretamente, o que não quer dizer que ele não será útil. Como $lim_{x \to + \infty} \frac{1}{x^{2} + 1} = 0$ , pela definição de limite com $x \to + \infty$ , existe $k > 0$ tal que $f (k) < \frac{1}{π}$ (se o valor de $f$ se aproxima de 0 quando $x \to + \infty$ , ele obviamente terá que ser menor que $\frac{1}{π}$ em algum valor de $x$ ). Assim, temos $f (k) < \frac{1}{π} < f (0) = 1$ e, como $f$ é contínua em $[0, k]$ , existe $c \in (0, k)$ , tal que $f (c) = \frac{1}{π}$ .

Exemplo 3

Todo polinômio de grau ímpar possui pelo menos uma raiz real. Seja $p (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + . . . + a_{1} x + a_{0}$ , com $n$ ímpar e $a_{n} \neq 0$ . Suponha inicialmente que $a_{n} > 0$ e, neste caso, teremos $lim_{x \to + \infty} p (x) = + \infty$ e $lim_{x \to - \infty} p (x) = - \infty$ . Assim, existem $a < 0$ e $b > 0$ tais que $p (a) < 0 < p (b)$ e, como $p$ é uma função contínua em $[a, b]$ , o TVI nos garante que existe $c \in (a, b)$ , tal que $p (c) = 0$ . Se, por outro lado, tivéssemos $a_{n} < 0$ , então $lim_{x \to + \infty} p (x) = - \infty$ e $lim_{x \to - \infty} p (x) = + \infty$ e poderíamos tomar $a < 0, b > 0$ tais que $p (a) > 0 > p (b)$ , e o resultado seguiria da mesma forma.

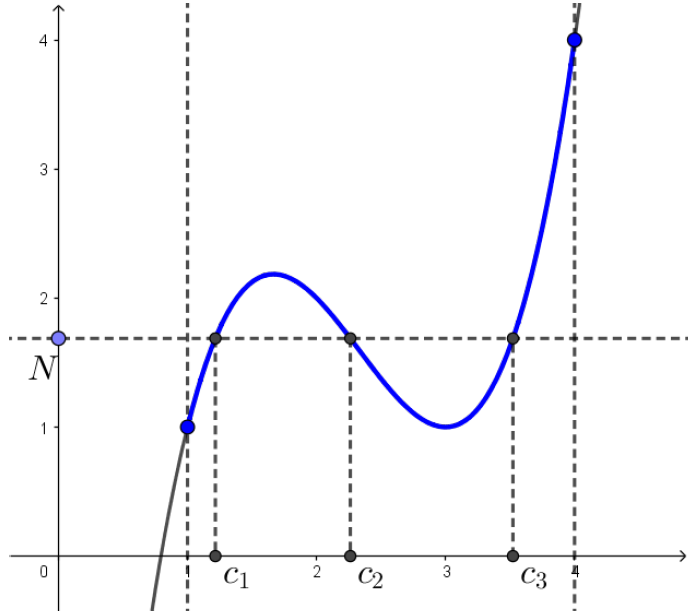
Observação: Como visto no Exemplo 1, na conclusão do Teorema do Valor Intermediário, pode existir mais de um valor para

c

tal que

f (c) = N

. No exemplo abaixo, podemos ver que, existem três valores distintos

c_{1}

c_{2}

c_{3}

no intervalo

(a, b)

tais que

f (c_{1}) = f (c_{2}) = f (c_{3}) = N

Exemplo 4

Este exemplo mostra que a conclusão do Teorema do Valor Intermediário não é válida, em geral, para funções descontínuas. Consideremos a função $f : [0, 1] \to R$ , definida por $f (x) = 0$ se $0 \leq x < \frac{1}{2}$ e $f (x) = 1$ se $\frac{1}{2} \leq x \leq 1$ .

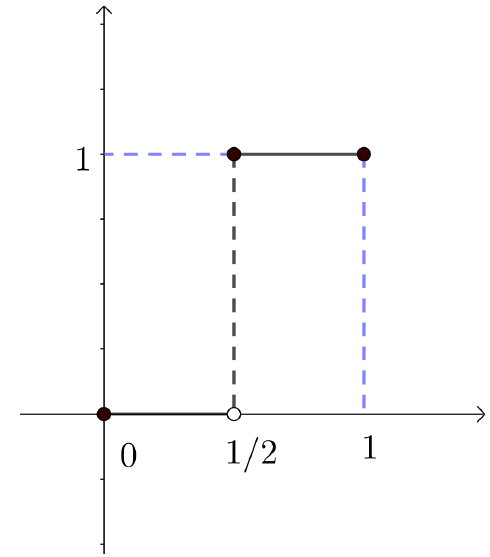
A função $f$ não é contínua em $[0, 1]$ já que não é contínua em $\frac{1}{2}$ . Se tomarmos qualquer número real $N$ , com $f (0) = 0 < N < 1 = f (1)$ , não é possível encontrar $x \in (0, 1)$ com $f (x) = N$ . Isto significa que a conclusão do TVI não é válida para a função $f$ . Isto, obviamente, não indica que o teorema não escteja correto, mas sim que esta função não satisfaz suas hipóteses ( $f$ não é contínua em $[a, b]$ ).
Observe que bastou um único ponto de descontinuidade em $[0, 1]$ para o TVI não poder ser aplicado à função $f$ .

Existência de raízes de equações

O TVI é muito utilizado para garantir a existência de raízes de equações, e até mesmo para dar uma estimativa destas raízes, quando a equação pode ser escrita na forma

f (x) = c

. Vejamos alguns exemplos.

Exemplo 5

Mostrar que a equação $4 x^{3} - 6 x^{2} + 3 x - 2 = 0$ tem uma raiz no intervalo $(1, 2)$ .

Solução

A equação pode ser escrita como $f (x) = 0$ , onde $f (x) = 4 x^{3} - 6 x^{2} + 3 x - 2$ . Note que, por ser uma função polinomial, $f$ é contínua em $[1, 2]$ .

Temos $f (1) = 4 - 6 + 3 - 2 = - 1 < 0$ e $f (2) = 32 - 24 + 6 - 2 = 12 > 0$ . Assim, $f (1) < 0 < f (2)$ , logo $N = 0$ é um número entre $f (1)$ e $f (2)$ . Como $f$ é contínua, o TVI nos garante que existe $c \in (1, 2)$ , tal que $f (c) = 0$ , o que implica que $4 x^{3} - 6 x^{2} + 3 x - 2 = 0$ tem pelo menos uma raiz em $(1, 2)$ .

Exemplo 6

Provar que existe $x \in R$ , tal que $x = \cos^{3} (x) + {sen}^{3} (x)$ .

Solução

Seja $f (x) = x - \cos^{3} (x) - {sen}^{3} (x)$ . Note que $f (x) = 0$ se, e somente se, $x = \cos^{3} (x) + {sen}^{3} (x)$ , assim, buscar uma raiz para a equação é equivalente a encontrar $x$ tal que $f (x) = 0$ .

Temos $f (0) = 0 - \cos^{3} (0) - {sen}^{3} (0) = - 1$ e $f (\frac{π}{2}) = \frac{π}{2} - \cos^{3} (\frac{π}{2}) - {sen}^{3} (\frac{π}{2}) = \frac{π}{2} - 0^{3} - 1^{3} = \frac{π}{2} - 1 > 0$ , pois $π > 2$ . Assim, $f (0) < 0 < f (\frac{π}{2})$ e, como $f$ é contínua em $[0, \frac{π}{2}]$ , existe $x \in (0, \frac{π}{2})$ tal que $f (x) = 0$ , logo $x = \cos^{3} (x) + {sen}^{3} (x)$ .

Exemplo 7

Localize uma raiz de $f (x) = \sqrt{x^{3} + 1} - 2 x$ em um intervalo de comprimento 1.

Solução

Observe que $f (0) = 1 > 0$ e $f (1) = \sqrt{2} - 2 < 0$ . Como a $f$ é contínua em $[0, 1]$ , pois $\sqrt{x^{3} + 1}$ é composta de contínuas e $2 x$ também é contínua, o TVI nos diz que, existe $c \in (0, 1)$ , tal que $f (c) = 0$ . Portanto, $x = c$ é uma raiz da função $f$ .

Exemplo 8

Mostre que os gráficos de $f (x) = x^{3} - x^{2}$ e $g (x) = x + 1$ possuem um ponto de interseção no intervalo $[1, 2]$ .

Solução

Precisamos mostrar que $f (x) = g (x)$ para algum $x \in [1, 2]$ , mas esse fato equivale a mostrar que $f (x) - g (x) = 0$ para algum $x \in [1, 2]$ . Definimos $h (x) = f (x) - g (x)$ , para $x \in [1, 2]$ . Observe que $h$ é contínua em $[1, 2]$ , $h (1) = - 2 < 0$ e $h (2) = 2^{3} - 2^{2} - 2 - 1 = 1 > 0$ , portanto pelo TVI, existe $c \in (1, 2)$ , tal que $h (c) = 0$ , ou seja, $f (c) = g (c)$ .