
Vimos que, em cada ponto $x_0$, a derivada pode ser calculada como o limite da razão:
$$\frac{f(x)-f(x_0)}{x-x_0}.$$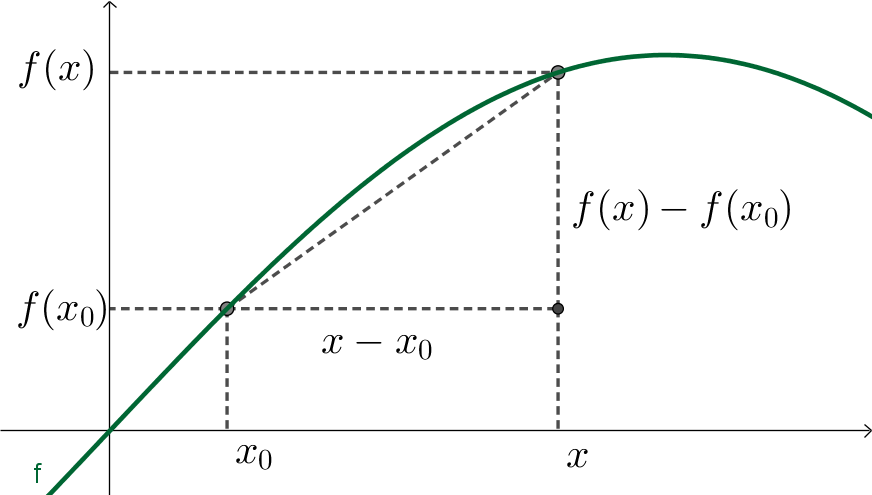
A razão mede a inclinação da corda
Observe, na Figura (REF NÃO APARECENDO) que essa razão é, para cada $x$, a inclinação da corda do arco do gráfico entre $(x,f(x))$ e $(x_0, f(x_0))$.
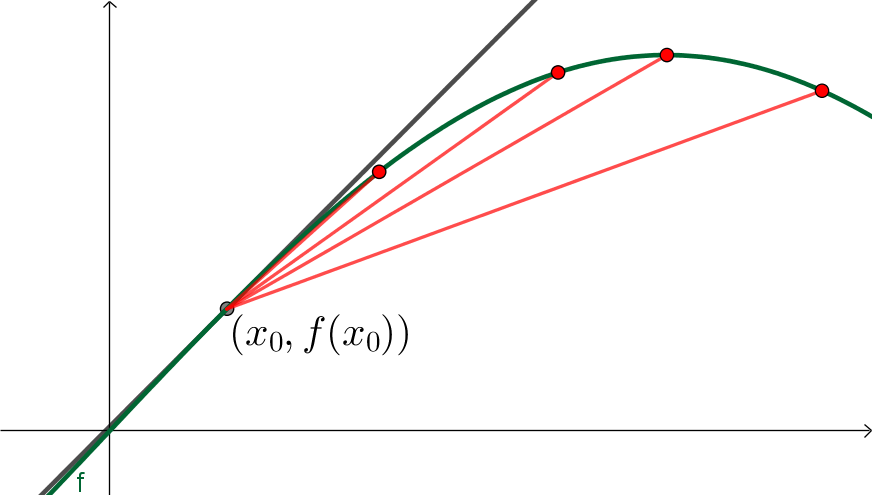
$x$ se aproxima de $x_0$
Quando $x$ se aproxima de $x_0$, a direção da corda se aproxima da direção tangente ao gráfico. No limite, temos a direção tangente.
Vemos, então, que $f'(x_0)$ é o coeficiente angular da reta tangente ao gráfico de $f$ em $(x_0,f(x_0))$.
Qual será, então, a equação da reta tangente? Como o coeficiente angular é $f'(x_0)$, temos:
$$y = f'(x_0)x+b .$$Como $(x_0,f(x_0))$ é um ponto da reta, escrevemos $ y = f(x_0) + f'(x_0)(x-x_0)$ e a expressão está dada. Note que a equação dessa reta é exatamente a aproximação que buscamos quando definimos derivada. Nesse momento, é conveniente organizar um pouco o que já sabemos.
Inicialmente procuramos uma aproximação para $f(x)$, perto de $x = x_0$, da forma:
$$f(x) \approx f(x_0) + a (x-x_0).$$Fizemos algumas restrições sobre as propriedades dessa aproximação.
Definimos a derivada como sendo o valor de $a$ na aproximação, quando existisse.
Nesse caso, passamos a denotar a derivada por $f'(x_0)$ e, consequentemente, a escrever:
$$f(x) \approx f(x_0) + f'(x_0) (x-x_0).$$Verificamos que, se a aproximação existisse, $f'(x_0)$ poderia ser calculada como:
$$f'(x_0) = \lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}.$$Verificamos que o valor desse limite é o coeficiente angular da reta tangente ao gráfico de $f$ no ponto $(x_0,f(x_0)).$
Concluímos que a reta que aproxima $f$, na nossa pergunta inicial, é justamente essa reta tangente.
Vamos explorar um pouco todas as informações que obtivemos até agora.
Se $f(x) = 3x + \beta$, qual será a derivada de $f$ em algum ponto do seu domínio?
No caso dessa função, o gráfico já é uma reta. A tangente a qualquer reta, em qualquer ponto, é a própria reta. E como a derivada mede o coeficiente angular da reta tangente ao gráfico, concluímos que, em qualquer valor de $x$, $f'(x) = 3$.
Se $f(x) = x^2$, quanto vale a derivada de $f$ em $x=0$?
Não é difícil ver que a reta tangente ao gráfico de $f$ em $(0,0)$ é o próprio eixo $\hat{x}$, que tem coeficiente angular $0$. Portanto, $f'(0) = 0$.
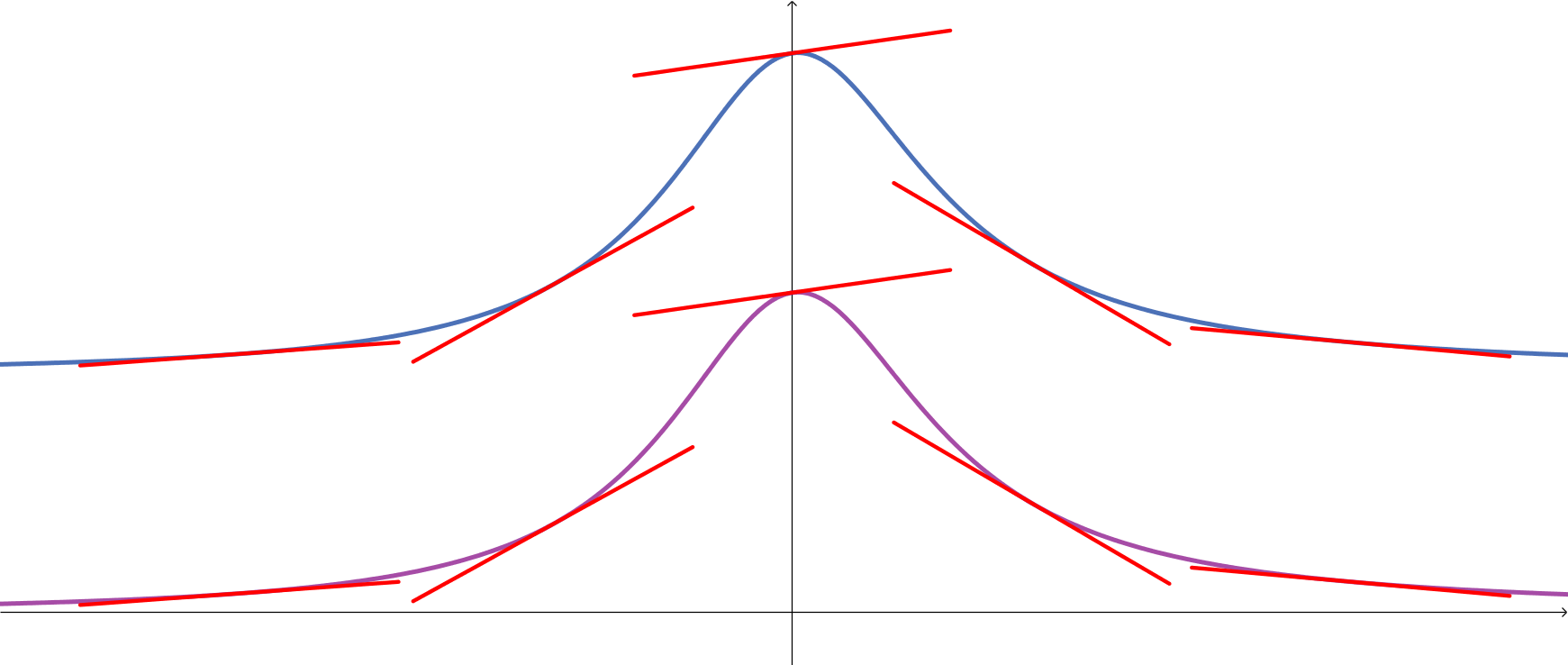
Como comparamos as derivadas de duas funções cuja diferença é uma constante? Observe que as direções tangentes não se alteram quando deslocamos o gráfico verticalmente. Nesse caso, as derivadas, em cada ponto, são iguais.
Conhecendo o gráfico da função é possível determinar o sinal da derivada. Na figura a seguir vemos que o coeficiente angular da reta tangente é positivo para valores de $x$ menores que $A$, muito próximo a $0$ em $x=A$ e negativo em $x>A$.
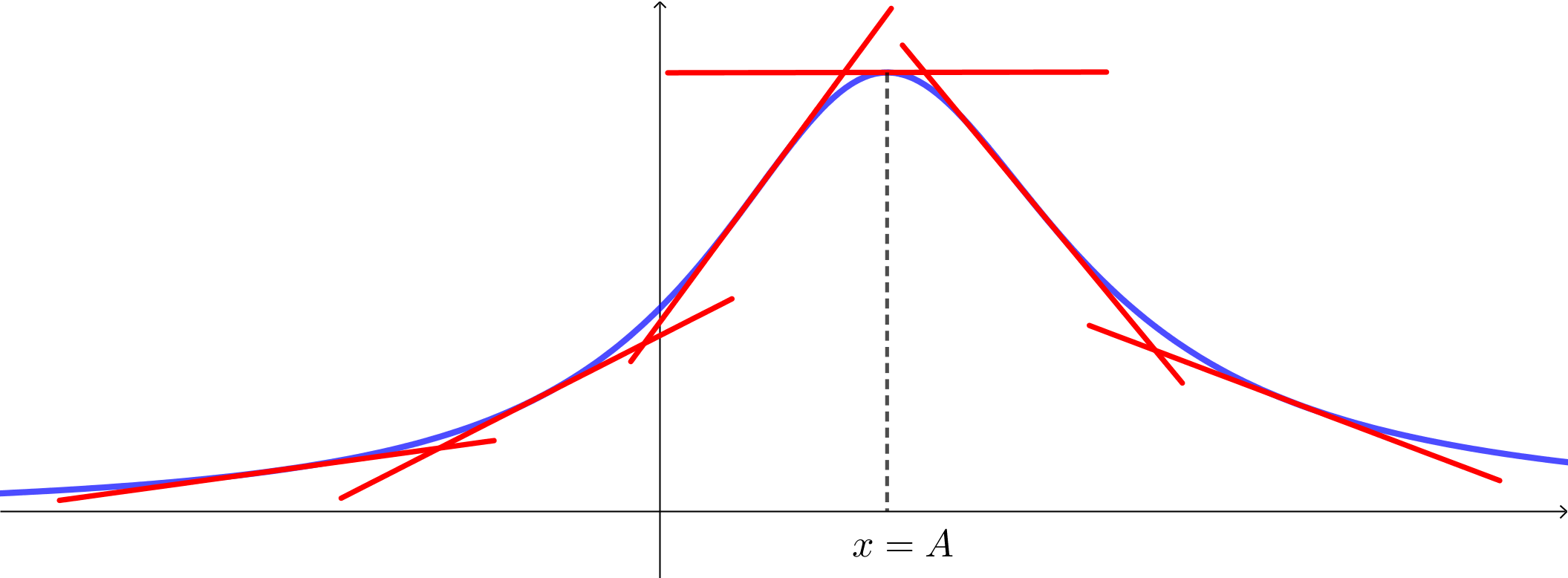
Suponha que a figura acima representa o gráfico de uma função $f(x)$. A pergunta chave é: existe relação entre o sinal da derivada e alguma propriedade de $f$? Vamos analisar o comportamento da função imaginando que caminhamos sobre o eixo $x$, começando em algum valor de $x<A$. É possível ver que, à medida que $x$ cresce, os valores de $f(x)$ também aumentam até que chegamos a $x=A$, quando o valor de $f(x)$ atinge um máximo. Dizemos, nesse caso, que existe um intervalo $(A- b, A), \; b>0$, no qual $f$ é crescente. Observamos que, nesse intervalo, o sinal da derivada é positivo.
Se continuarmos caminhando sobre o eixo $x$ a partir de $A$, sempre na direção positiva, vemos que à medida que $x$ cresce, o valor de $f(x)$ diminui. Nesse caso, constatamos que existe um intervalo $(A, A+b), \; b>0$, em que $f$ é uma função decrescente. Notamos que nesse intervalo o sinal da derivada é negativo.
A partir dessas observações, é natural investigar se essa associação entre o sinal da derivada e o crescimento/decrescimento de uma função é uma propriedade que vale para uma função diferenciável qualquer.
Dada uma função $f$ qualquer, diferenciável em algum intervalo $I$, vamos fixar $x_0$ em I. Suponha que $f'(x_0)$ é positivo. Para algum $x \in I$, escrevemos:
\begin{equation}\tag{1}f(x) = f(x_0) + f'(x_0)(x-x_0) + erro(x)\end{equation}Imagine que, na equação 1, $x>x_0$ e que $x$ está suficientemente próximo de $x_0$ de tal modo que o valor de $erro(x)$ é desprezível.
Podemos supor isso pela definição de derivada
Nesse caso, podemos dizer que $f'(x_0)(x-x_0)>0$ (pois $f'(x_0)>0$ e $x>x_0$) e, portanto, $f(x)>f(x_0)$. Por outro lado, se $x<x_0$, $f'(x_0)(x-x_0)$ é negativo e $f(x)<f(x_0)$. Argumentando desse modo, é possível mostrar que se $f'(x_0)>0$ existe um intervalo em torno de $x_0$ no qual $f$ é crescente. Analisando a mesma expressão 1 também é possível concluir que, se $f$ é diferenciável e crescente em um intervalo, a derivada de $f$ é não negativa nesse intervalo. Basicamente, se $f$ é crescente, $f(x)>f(x_0)$ quando $x>x_0$ e, para que isso aconteça, $f'(x_0)$ não pode ser negativa de acordo com a expressão. Aqui, é importante observar que, em alguns casos, se a função é crescente em um intervalo, a derivada pode se anular em pontos isolados desse intervalo como no exemplo de
$$f(x) = x^3,$$discutido ao final dessa seção. Todavia, não será negativa em ponto algum.
Um raciocínio análogo permite concluir que $f'(x_0)<0$ então existe um intervalo em torno de $x_0$ no qual $f$ é decrescente. Por exclusão, podemos concluir que $f'(x)$ vale $0$ em um intervalo se e somente se $f$ é constante naquele intervalo (faça um desenho para entender essa afirmação geometricamente).
Para organizar as ideias, escrevemos:
Seja $f(x)$ uma função diferenciável em um intervalo $I$. Então:
Se para algum $x_0 \in I$, $f'(x_0)>0$ então existe um Intervalo $J_{x_0} \subset I$ em torno de $x_0$ em que $f$ é crescente.
Se para algum $x_0 \in I$, $f'(x_0)<0$ então existe um Intervalo $J_{x_0} \subset I$ em torno de $x_0$ em que $f$ é decrescente.
Se $f$ é crescente em um intervalo $J \subset I$, então $f'(x) \geq 0$ se $x \in J$.
Se $f$ é decrescente em um intervalo $J \subset I$, então $f'(x) \leq 0$ se $x \in J$.
Se em algum intervalo $J \subset I$, $f'(x)=0$, então $f$ é constante em $J$.
Esta última afirmação é mais sutil. Veremos mais adiante no curso, que decorre do Teorema do Valor Médio.
Observe no próximo exemplo que a derivada pode ser nula em algum ponto no interior de um intervalo onde a função é crescente (ou decrescente).
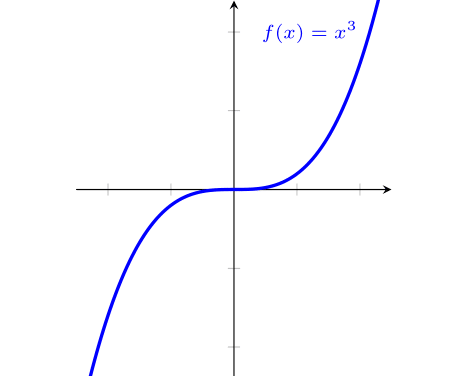
Considere a função $f(x)=x^3$. Como pode ver no gráfico abaixo, a função é crescente em todo o seu domínio e $f'(x)$ se anula apenas no ponto $x=0$, sendo positiva em todos os outros pontos.
Vimos alguns exemplos de como explorar o que já sabemos sobre derivadas, usando o gráfico. A lista de exercícios cuida bastante dessa ideia também.