
Considere as equações a seguir:
$y=-3x-2$ $\space$ e $\space$ $y=2(x+1)-3$
Esboce os gráficos das retas acima identificando as interseções com os eixos coordenados.
Estude o sinal das expressões dadas.
Gráfico de $y=-3x-2$
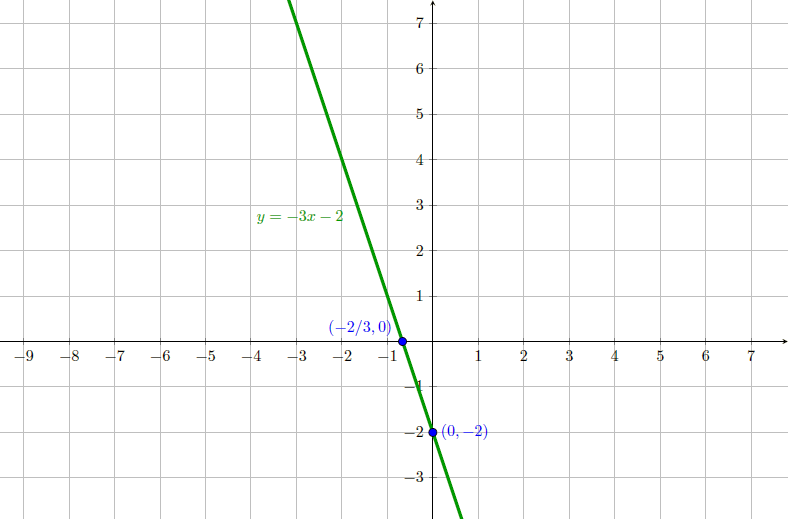
Gráfico de $y=2(x+1)-3$
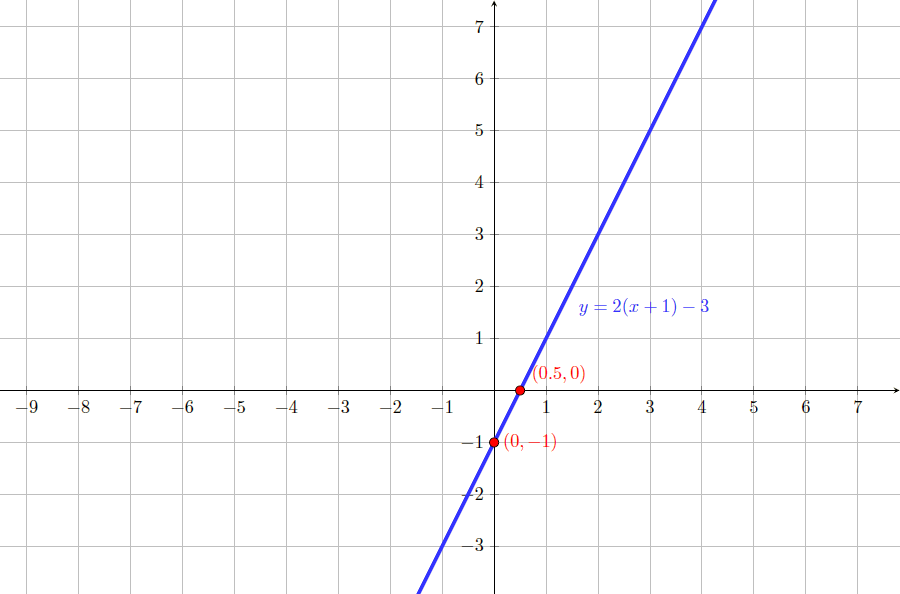
Estudo do sinal das expressões anteriores:
$$y=2(x+1)-3<0 \iff x>\frac{1}{2};$$ $$y=2(x+1)-3=0 \iff x=\frac{1}{2}.$$
Determine a equação da reta que contém o ponto $(1,-1)$ e cujo coeficiente angular é igual a $-4$. Esboce esta reta, identificando as interseções com os eixos coordenados.
A equação da reta é $y=-4x+3$, com gráfico:
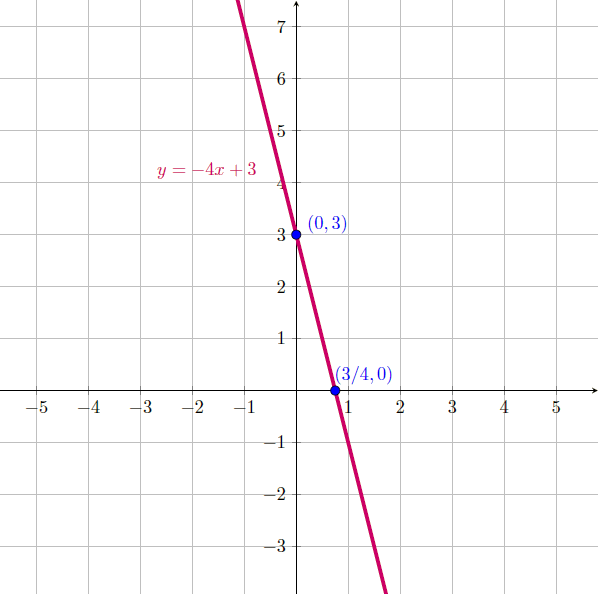
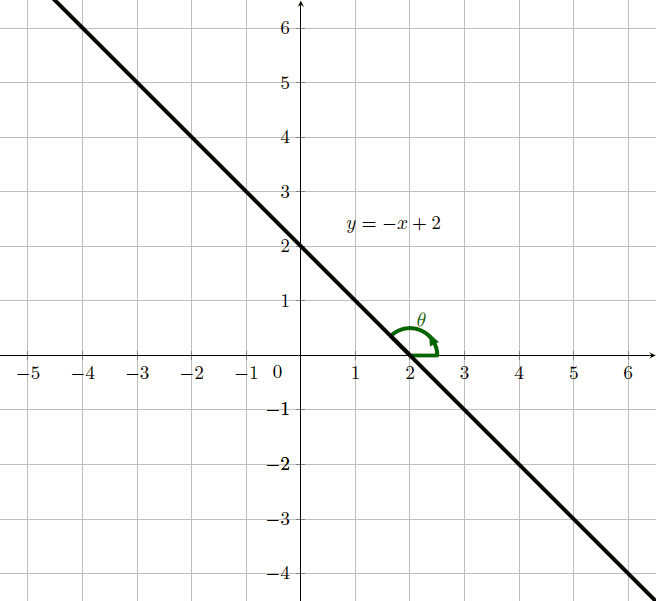
Esboce o gráfico da expressão $y=-x+2$, identifique na figura o ângulo $\theta$, tal que $\mathrm{tg} \theta=-1$ (inclinação da reta). Qual o valor de $\theta$ em radianos?
$\theta = \dfrac{3\pi}{4} radianos$, e o gráfico de $y=-x+2$ é:
Determine a equação da reta esboçada abaixo e suas interseções com os eixos coordenados.
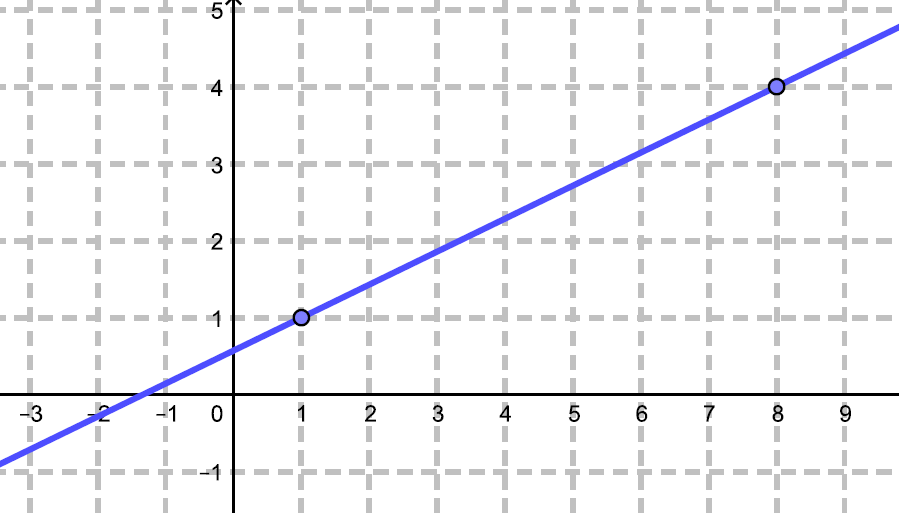
(Dica: Há dois pontos marcados que temos certeza de suas coordenadas, use-os)
A equação da reta é $y=\frac{3}{7}x+\frac{4}{7}$. As interseções com os eixos coordenados são os pontos $(0,\frac{4}{7})$ e $(-\frac{4}{3}, 0)$.
Em cada item abaixo, encontre as raízes reais (se possível), estude o sinal e esboce o gráfico, indicando e marcando as coordenadas do vértice.
$y=4x^2+3x-1$
$y=-2x^2+x+3$
$y=x^2-2\sqrt{2}x+2$
$y=-4x^2-4x-1$
$y=x^2+x+1$
$y=-2x^2+x-4$
$y=4x^2+3x-1$
Raízes: $x=-1$ e $x=\frac{1}{4}$
Estudo de sinal:
$$4x^2+3x-1>0 \iff x<-1 \text{ ou } x>\frac{1}{4}$$.
$$4x^2+3x-1<0 \iff -1 < x < \frac{1}{4}$$.
$$4x^2+3x-1=0 \iff x=-1 \text{ ou } x=\frac{1}{4}$$Gráfico:
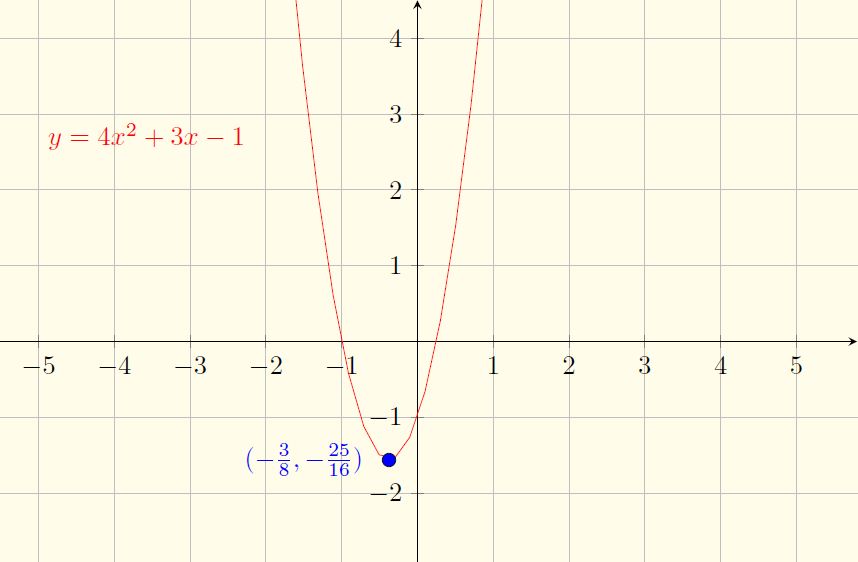
$y=-2x^2+x+3$
Raízes: $x=\frac{3}{2}$ e $x=-1$
Estudo de sinal:
$$-2x^2+x+3>0 \iff -1<x<\frac{3}{2}$$ $$-2x^2+x+3<0 \iff x<-1 \text{ ou } x>\frac{3}{2}$$ $$-2x^2+x+3=0 \iff x=-1 \text{ ou } x=\frac{3}{2}$$Gráfico:
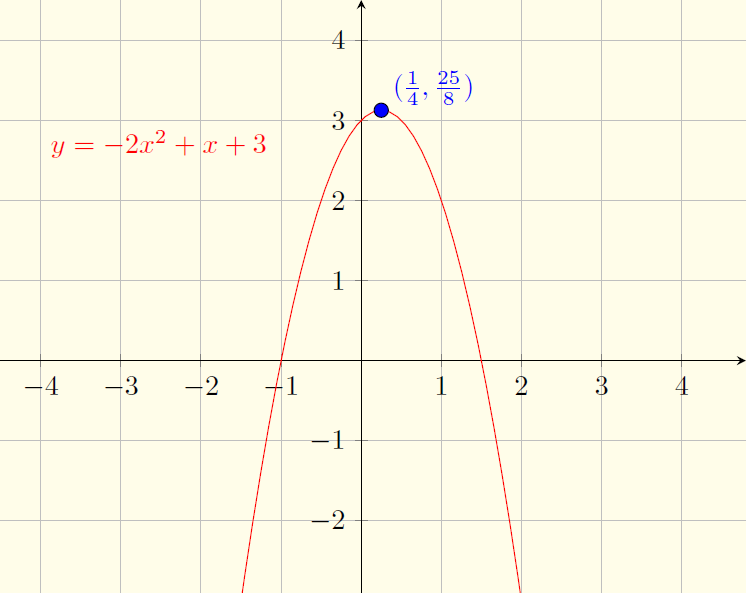
$y=x^2-2\sqrt{2}x+2$
Raízes: $x=\sqrt{2}$
Estudo de sinal:
$$x^2-2\sqrt{2}x+2>0 \iff x<\sqrt{2} \text{ ou } x>\sqrt{2}$$ $$x^2-2\sqrt{2}x+2>0 \iff x=\sqrt{2}$$Gráfico:
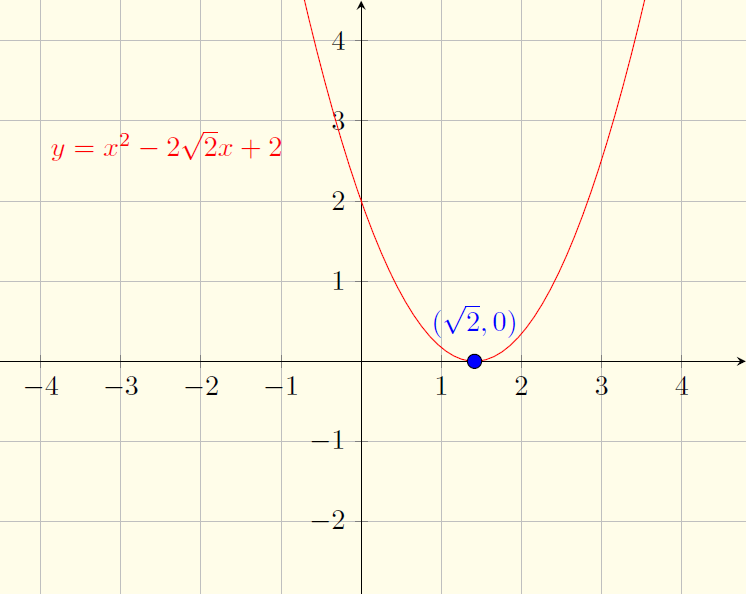
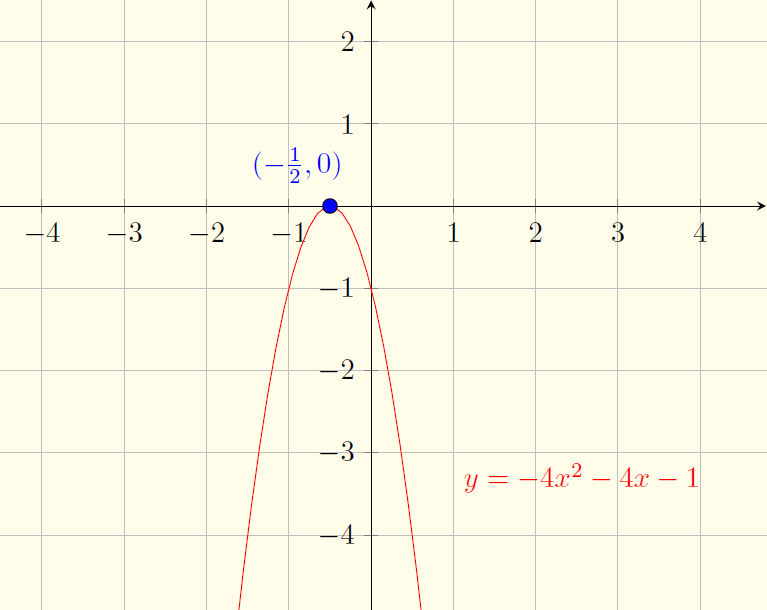
$y=-4x^2-4x-1$
Raízes: $x=-\frac{1}{2}$
Estudo de sinal:
$$y=-4x^2-4x-1<0 \iff x<-\frac{1}{2} \text{ ou } x>-\frac{1}{2}$$ $$y=-4x^2-4x-1=0 \iff x=-\frac{1}{2}$$Gráfico:
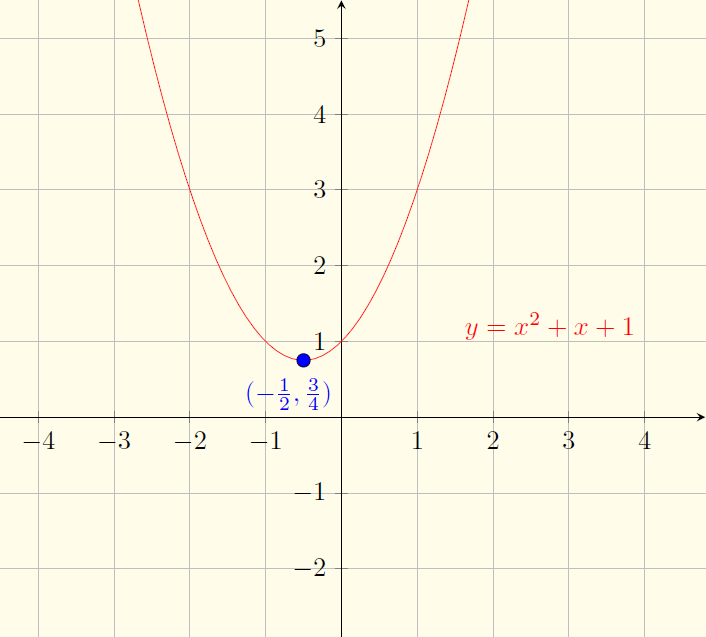
$y=x^2+x+1$
Raízes: Não existem raízes reais.
Estudo de sinal: $x^2+x+1>0$, para todo $x\in\mathbb{R}$.
Gráfico:
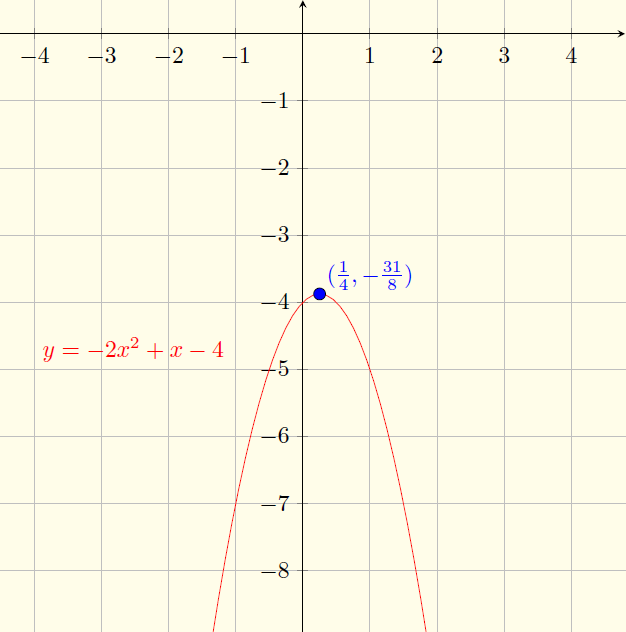
$y=-2x^2+x-4$
Raízes: Não existem raízes reais.
Estudo de sinal: $-2x^2+x-4>0$, para todo $x\in\mathbb{R}$.
Gráfico:
Fatore as expressões dos itens de (1) a (4) do exercício anterior.
Para a fatoração, vamos usar as raízes reais encontradas no exercício anterior.
$y=4x^2+3x-1=4(x+1)(x-\frac{1}{4})$
$y=-2x^2+x+3=2(x-\frac{3}{2})(x+1)$
$y=x^2-2\sqrt{2}x+2=(x-\sqrt{2})^2$
$y=-4x^2-4x-1=-4(x+\frac{1}{2})^2$
Um projétil é lançado do solo verticalmente para cima. Ao fim de $t$ segundos, atinge a altura $y(t)$ em metros, dada por $y(t)=40t-5t^2$.
Calcule a altura atingida pelo projétil $2s$ após seu lançamento.
Determine a altura máxima atingida pelo projétil.
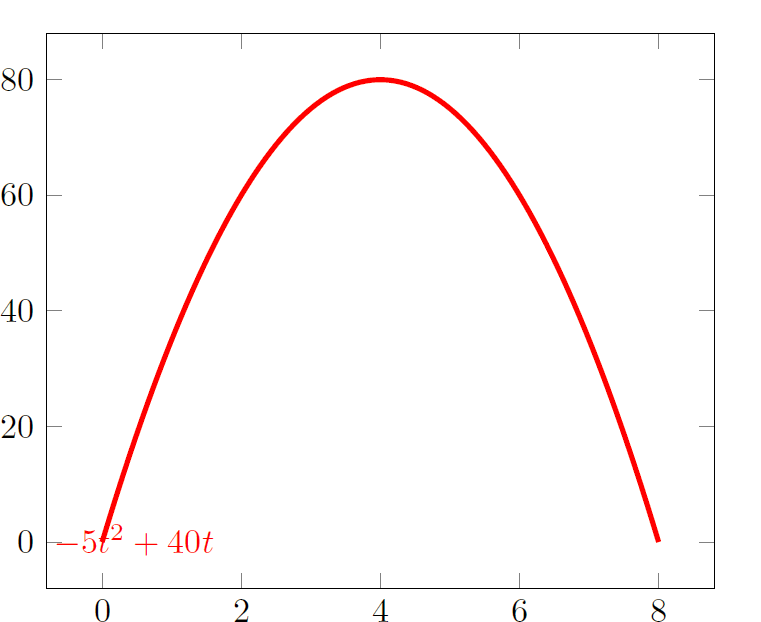
Esboce o gráfico da função que representa a altura do projétil, para $0\leq t \leq 8$.
Calcule em quanto tempo o projétil atinge a altura de $75m$, durante a subida.
Calculamos $y(2)=60 \text{ metros}$.
O gráfico de $y(t)$ é uma parábola com concavidade para baixo, portanto a altura máxima é atingida em seu vértice, $t_{v}=4$ e $y(t_{v})=y(4)=80 \text{ metros}$.
Gráfico em $0\leq t\leq 8$:
Devemos resolver a equação $y(t)=75 \iff 40t-5t^2 = 75 \iff t^2-8t + 15 = 0$. As raízes são $t=3$ e $t=5$, como pede-se no momento da subida, consideramos o menor valor do tempo. Assim, o tempo é em $t=3$ segundos.
Considere todos os possíveis retângulos que possuem perímetro igual a $80 \text{ cm}$. Dentre estes retângulos, determine aquele que terá a área máxima. Qual será essa área?
Vamos chamar os lados do retângulo de $x$ e $y$, por hipótese o perímetro $2x + 2y$ é igual a $80$, logo $2x+2y=80 \iff y=40-x$. A área é dada pela função quadrática $A(x)=x(40-x)=40x-x^2, x>0$. Seu gráfico tem concavidade para baixo, logo no vértice ocorre o ponto de máximo da área, a saber, $x_{v}=20$. Portanto, um dos lados mede $20\text{ cm}$ e o outro também, pois $y=40-x=20$. Assim, entre esses retângulos, o de maior área é o quadrado de lado $20\text{ cm}$, cuja área é $400\text{ cm}^2$:
Resolva as inequações abaixo e forneça as respostas usando notação de intervalo.
$-x^2+4x<0$
$\dfrac{2x^2+x+1}{x-1}>0$
$\dfrac{x^2}{x+3}>\dfrac{4}{x+3}$
Estudamos o sinal de $-x^2 + 4x$, cujas raízes são $0$ e $4$ com concavidade para baixo, logo $-x^2+4x<0$ em $(-\infty; 0) \cup (4,\infty)$.
Devemos fazer o produto dos sinais das expressões que aparecem no numerador e no denominador. O numerador é sempre positivo, pois não possui raízes reais e a concavidade da parábola associada é para cima, logo o sinal depende apenas do sinal do denominador (que não pode se anular) que é positivo se $x>1$. Logo, o conjunto solução é igual a $(1,\infty)$.
Cuidado, não pode cancelar o denominador, pois $x+3$ troca de sinal! Ou seja, $x+3<0$ quando $x<-3$, o que levaria a uma inversão do sinal “$>$” e para $x>-3$ não haveria a inversão, o que implicaria na abertura de dois casos diferentes e mais trabalho... Assim, vamos escrever uma inequação equivalente:
$$\frac{x^2}{x+3}>\frac{4}{x+3} \iff \frac{x^2}{x+3}-\frac{x^2}{x+3}>0 \iff \frac{x^2-4}{x+3}>0$$Agora, podemos fazer o produto dos sinais entre a expressão $x^2-4$ e $x+3$, para obter que $\dfrac{x^2-4}{x+3}$ é positiva quando $x\in(-3,-2)\cup(2,\infty)$.
Determine o maior subconjunto da reta onde as funções abaixo estão bem definidas (domínio maximal).
$f(x)=\dfrac{x-2}{9-x^2}$
$f(x)=\sqrt{4x-x^2}$
$f(x)=\dfrac{x}{\sqrt{x^2+4x+5}}$
($\star$) Domínio maximal de uma função real é o maior subconjunto da reta real, onde a função está bem definida.
$\{x\in\mathbb{R};x\neq\pm3\}$
$\{x\in\mathbb{R};0\leq x\leq 4\}$
Todo número real, ou seja, $\mathbb{R}$.
Quais os subconjuntos da reta abaixo podem ser utilizados como domínio para a função $f(x)=\dfrac{x}{\sqrt{4-x^2}}$.
$[-2,0)\cup (0,2]$
$(-2,1]$
$(0,+\infty)$
$[-0.1,1.99] $
$[-1.999....,1.999...)$
$\{0,\pm \frac{1}{2},\pm 1\}$
A restrição para que a expressão dada esteja bem definida é $4-x^2>0 \iff x\in (-2,2)$. Portanto, qualquer subconjunto de $(-2, 2)$ pode ser usado como domínio.
$[-2, 0) \cup (0; 2]$, não pode, pois $-2$ e $2$ não pertencem ao intervalo aberto $(-2,2)$:
$(-2, 1]$, pode.
$(0,+\infty)$, não pode.
$[-0.1, 1.99]$, pode, já que $1,99<2$.
$[-1.999...., 1.999...)$, não pode, pois $-1.999... =-2$, logo $[-1.999...., 1.999...)=[-2,2)$ não está contido em $(-2,2)$.
$\{0,\pm\frac{1}{2},\pm1\}$, pode.
Quais das funções abaixo possuem o mesmo conjunto imagem da função de expressão $f(x)=x^2+2, \ x\in(-2,1]$.
$g(x)=x+\sqrt{2}, \ x\in [2-\sqrt{2},6-\sqrt{2})$
$g(x)=\dfrac{1}{x}+1, \ x\in (1/5,1]$
$g(x)=-2x, \ x\in (-2,-1]$
O gráfico da função $f$ é um arco de parábola com vértice em $(0,2)$ e concavidade para cima. Observe que, $-2<x\leq 1 \Rightarrow 0\leq x^2<4 \Rightarrow 2 \leq x^2+2<6$, logo $Im(f)=[2,6)$.
$g(x)=x+\sqrt{2},x\in[2-\sqrt{2},6-\sqrt{2})$. O gráfico é um segmento de reta e $2-\sqrt{2}\leq x<6-\sqrt{2} \iff 2 \leq x+\sqrt{2}<6$, logo $Im(f)=[2,6)$, portanto possui o mesmo conjunto imagem.
$g(x)=\dfrac{1}{x}+1, x\in (1/5,1]$. O gráfico é um arco de hipérbole e $1/5<x\leq 1 \iff 1\leq 1/x < 5 \iff 2 \leq 1+1/x<6$, logo $Im(f)=[2,6)$, portanto possui o mesmo conjunto imagem.
$g(x)=-2x, x\in (-2,-1]$. O gráfico é um segmento de reta e $-2<x\leq -1 \iff -4<2x\leq -2 \iff 4 > -2x\geq2$, logo $Im(f)=[2,4)$, portanto NÃO possui o mesmo conjunto imagem.
Verifique se cada afirmativa abaixo é falsa ou verdadeira, justificando.
Duas funções que possuem mesmo domínio e mesmo conjunto imagem são iguais.
Os gráficos das funções $f(x)=2$ e $g(x)=-1$, $x\in \mathbb{R}$ são retas verticais.
A reta $x=1$ é horizontal.
As funções $f(x)=\dfrac{4x^2-1}{2x+1}$ e $g(x)=2x-1$, definidas em seus respectivos domínios maximais, são iguais.
O gráfico da função $f(x)=3x^2+x+1, x\in \mathbb{R}$ é uma parábola com concavidade para cima, que não possui interseção com os eixos coordenados.
O gráfico da função $f(x)=\dfrac{x^4-16}{x^2+4}, x\in \mathbb{R}$ é uma parábola com concavidade para cima, simétrica em relação ao eixo $y$, que possui interseção com o eixo $y$ no ponto $(0,-4)$.
Falsa. Para duas funções serem iguais, devem ter o mesmo domínio, a mesma imagem em cada ponto do domínio e além disso o contradomínio também deve ser o mesmo. Por exemplo, as seguintes funções possuem mesmo domínio $\mathbb{R}$ e mesmo conjunto imagem $\mathbb{R}$, mas são diferentes:
\[\begin{array}{cccc}f : & \! \mathbb{R} & \! \longrightarrow &\! \mathbb{R} \\ & \! x & \! \longmapsto & \! x.\end{array}\]e
\[\begin{array}{cccc}g : & \! \mathbb{R} & \! \longrightarrow &\! \mathbb{R} \\ & \! x & \! \longmapsto & \! -x.\end{array}\]Falsa. Essas retas são horizontais, por exemplo $f(x)=2, x\in\mathbb{R}$ significa que $y=2$, qualquer que seja o valor de $x$. Idem para $g$.
Falsa. Essa reta é vertical ($x=1$, qualquer que seja o valor de $y$).
Falsa. O domínio maximal da $g$ é $\mathbb{R}$, mas o domínio maximal da $f$ é $(-\infty,-1/2) \cup (-1/2;+\infty)$, pois o denominador não pode se anular. Então, seus domínios são diferentes. Logo, as funções não podem ser iguais, apesar de terem a mesma imagem em cada ponto de $(-\infty,-1/2) \cup (-1/2,+\infty)$
$$\left(f(x)=\frac{4x^2-1}{2x+1}=\dfrac{(2x-1)(2x+1)}{2x+1}=2x-1, \forall x\in(-\infty,-1/2)\cup(-1/2,+\infty).\right)$$Falsa. O gráfico possui interseção com o eixo $y$, a saber, no ponto $(0,1)$.
Verdadeira Primeiro, observe que $f(x)=\frac{(x^2-4)(x^2+4)}{x^2+4}=x^2-4, \forall x\in\mathbb{R}$, logo o gráfico da função $f$ coincide com o gráfico da função $g(x)=x^2-4, \forall x\in\mathbb{R}$, que é uma parábola com concavidade para cima, simétrica em relação ao eixo $y$, que possui interseção com o eixo $y$ no ponto $(0,-4)$.
Apresente uma expressão condicionalmente definida para a função $f: \mathbb{R} \rightarrow \mathbb{R}$ cujo gráfico está representado abaixo.
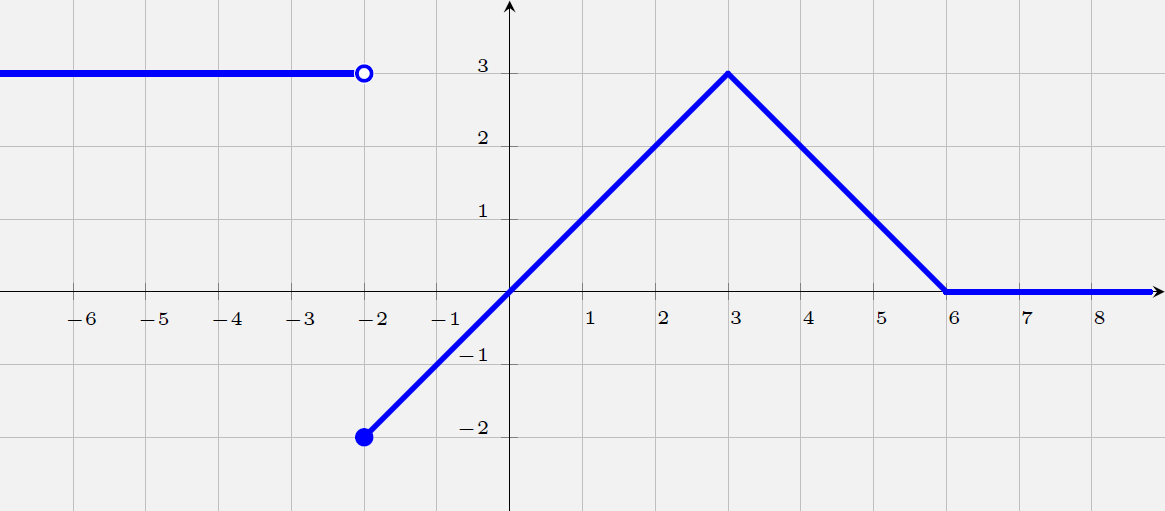
Para $x<-2$, a função é constante e igual a $3$. Para $-2\leqslant x\leqslant 3$, a função é linear com $f(x)=x$. Com $3<x\leqslant 6$, a função é afim com $f(x)=6-x$. Para $x\geqslant 6$, temos $f(x)=0$. Assim, podemos escrever
$$f(x)=\begin{cases} 3 & \text{se } x<-2 \\x & \text{se } -2 \leqslant x < 3 \\6-x & \text{se } 3 \leqslant x < 6 \\0 & \text{se } x \geqslant 6. \end{cases} $$Observe que pudemos escolher onde colocar a igualdade para $x=3$ e $x=6$, pois as expressões definidas em condições que têm extremos nestes pontos têm o mesmo valor. Não é o caso de $x=-2$.
Apresente uma definição para as funções listadas abaixo em que não apareçam módulos, utilizando definições condicionais e esboce o gráfico:
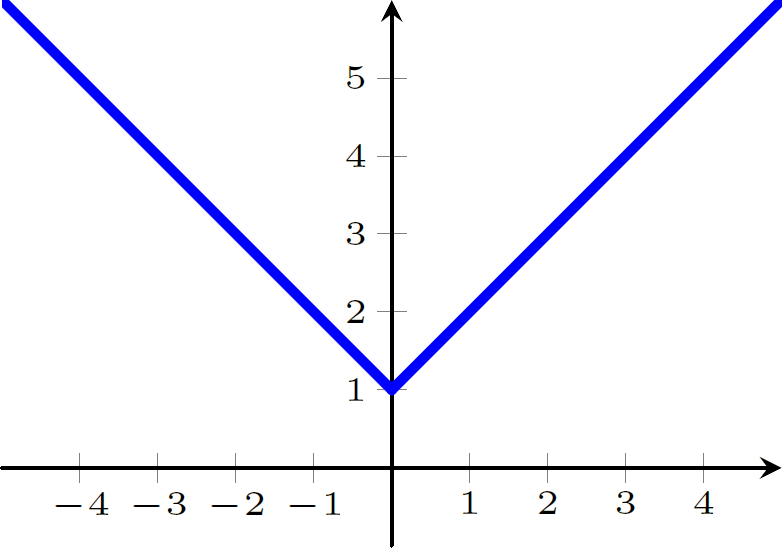
$f(x) = |x| + 1$
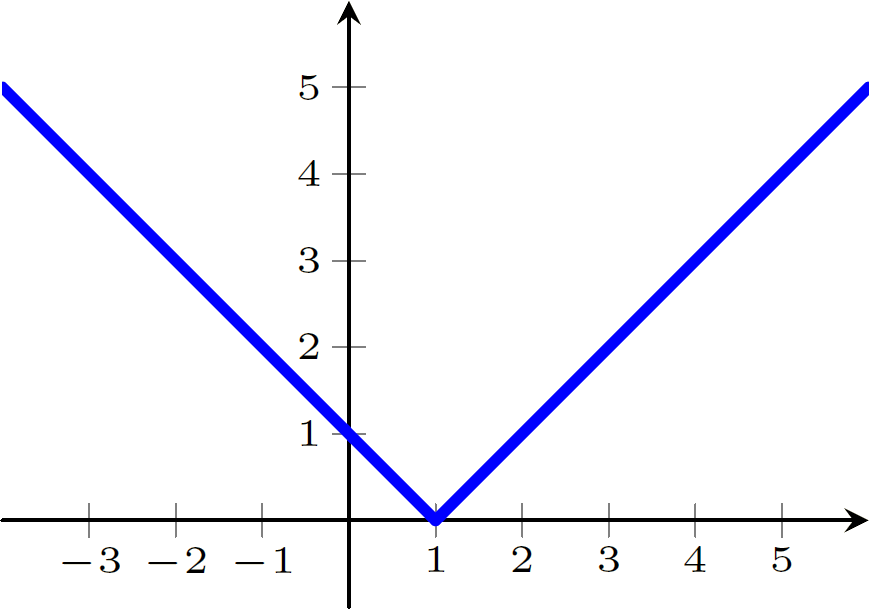
$f(x) = |x-1|$
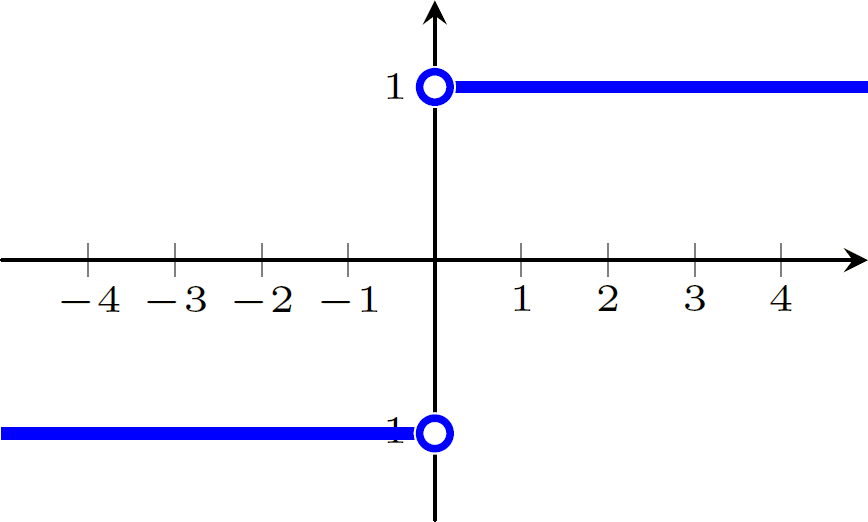
$f(x) = \dfrac{|x|}{x}$
$f(x)=\begin{cases} x+1 & \text{se } x\geqslant0 \\-x+1 & \text{se } x<0. \end{cases} $
$f(x)=\begin{cases} x-1 & \text{se } x\geqslant1 \\-x+1 & \text{se } x<1. \end{cases} $
$f(x)=\begin{cases}
x+1 & \text{se } x>0 \\-x+1 & \text{se } x<0.
\end{cases}
$
Esta função não está definida para $x=0$.
Se $x \in [0, \pi/2)$ é tal que $\mathrm{tg}(x) = \sqrt{5}$, determine $\mathrm{cos}(x)$ e $\mathrm{sen}(x)$.
Como $tg=\sqrt{5}$, temos que
$$\dfrac{\mathrm{sen}(x)}{\mathrm{cos}(x)}=\sqrt{5} \therefore \mathrm{sen}(x)=\sqrt{5}\space\mathrm{cos}(x).$$Além disso, como $\mathrm{cos}^2(x)+\mathrm{sen}^2(x)=1$, temos
$$\mathrm{cos}^2(x)+\left(\sqrt{5}\space\mathrm{cos}(x)\right)^2=1,$$logo
$$\mathrm{cos}^2(x)+5\mathrm{cos}^2(x)=1,$$e, portanto,
$$6\space\mathrm{cos}^2(x)=1.$$Assim,
$$cos^2(x)=\frac{1}{6},$$o que implica
$$\mathrm{cos}(x)=\pm\frac{1}{\sqrt{6}}.$$Como $x\in[0,\pi/2)$, seu cosseno será positivo, logo
$$\mathrm{cos}(x)=\frac{1}{\sqrt{6}}.$$Temos ainda
$$\mathrm{sen}(x)=\sqrt{5}\space\mathrm{cos}(x)=\frac{\sqrt{5}}{\sqrt{6}}.$$
Resolva, para $x \in \mathbb{R}$, as seguintes equações:
$\mathrm{sen} (x) = -\dfrac{\sqrt{2}}{2}$
$2\mathrm{cos}^2(x) = \mathrm{cos} (x)$
$S={x\in\mathbb{R}: x=5\pi/4+2k\pi \text{ ou } x=-\pi/4+2k\pi,k\in\mathbb{Z}}$
$S={x\in\mathbb{R}: x=\pm\pi/3+2k\pi \text{ ou } x=\pi/2+k\pi,k\in\mathbb{Z}}$
Determine o conjunto solução das inequações
$\mathrm{sen} (x) > - \dfrac{\sqrt{2}}{2}$
$\mathrm{tg} (x) < \sqrt{3}$
$\mathrm{cos} (x) \geqslant \dfrac{1}{2}$
$-\pi/4+2k\pi<x<5\pi/4+2k\pi$
$-\pi/2+k\pi<x<\pi/3+k\pi$
$-\pi/3+2k\pi\leqslant x\leqslant\pi/3+2k\pi$