
Determine o domínio das funções abaixo:
$f(x)=\displaystyle \sqrt{\frac{-2x^2+x-1}{4-x^2}}$
$f(x)=\displaystyle \frac{\sqrt[4]{3x^2+4x-1}}{5-2x}$
$f(t)=\displaystyle \frac{\displaystyle \frac{1}{t}}{t^3-2t^2}$
$g(s)=\displaystyle \frac{s}{\sqrt[3]{s-1}}+\sqrt{16-s^4}$
Devemos ter $\dfrac{-2x^2+x-1}{4-x^2}\geq0$, portanto vamos fazer o produto dos sinais entre o numerador e o denominador:
| $(-\infty,-2)$ | $-2$ | $(-2,2)$ | $2$ | $(2,+\infty)$ | |
| $-2x^2+x-1$ | $-$ | $-$ | $-$ | $-$ | $-$ |
| $4-x^2$ | $-$ | $0$ | $+$ | $0$ | $-$ |
| $\frac{2x^2+x-1}{4-x^2}$ | $+$ | $\nexists$ | $-$ | $\nexists$ | $+$ |
Logo, $\mathrm{D}(f)=(-\infty,-2)\cup(2,+\infty)$.
Devemos ter $5-2x\neq0$, ou seja, $x\neq5/2$ e além disso, $3x^2+4x-1\geq0$, pois a raiz é par. Obsevando que as raízes de $3x^2+4x-1=0$ são
$$x_{1}=\frac{-2+\sqrt{7}}{3} \space \text{ e } \space x_{2}=\frac{-2-\sqrt{7}}{3}$$e que a parábola associada a $y=3x^2+4x-1$ possui concavidade voltada para cima, temos que
$$3x^2+4x-1\geq0 \iff x\leq\frac{-2-\sqrt{7}}{3} \space \text{ ou } \space x\geq\frac{-2+\sqrt{7}}{3}.$$Assim,
$$\mathrm{D}(f)=\left(-\infty,\frac{-2-\sqrt{7}}{3}\right]\cup\left[\frac{-2+\sqrt{7}}{3},5/2\right)\cup(5/2,+\infty).$$Devemos ter $t\neq0$ e $t^3-2t^2\neq0$. Mas, $t^3-2t^2=t^2(t-2)=0 \iff t^2=0$ ou $t-2=0 \iff t=0$ ou $t=2$. Portanto, $t\neq0$ e $t\neq2$. Assim, $\mathrm{D}(f)=\mathbb{R} \backslash \{0,2\}$.
A raiz do denominador é ímpar, portanto está bem definida para qualquer número real. Mas, como está no denominador, não pode se anular, logo $s-1\neq0$, ou seja, $s\neq1$. A segunda raiz é par, logo devemos ter $16-s^4\geq0$. Vamos fatorar essa última expressão e estudar seu sinal: $16-s^4=(4-s^2)(4+s^2)$, onde $(4+s^2)>0, \forall s \in \mathbb{R}$, logo o sinal depende do sinal de $4-s^2$. Como $4-s^2\geq0 \iff s \in [-2,2]$, segue que $16-s^4\geq0 \iff s \in [-2,2]$. Consequentemente, $\mathrm{D}(f)=[-2,1)\cup(1,2]$.
Para cada uma das figuras abaixo, determine se a curva dada é o gráfico de uma função de $x$. Se for o caso, obtenha o domínio e a imagem da função.
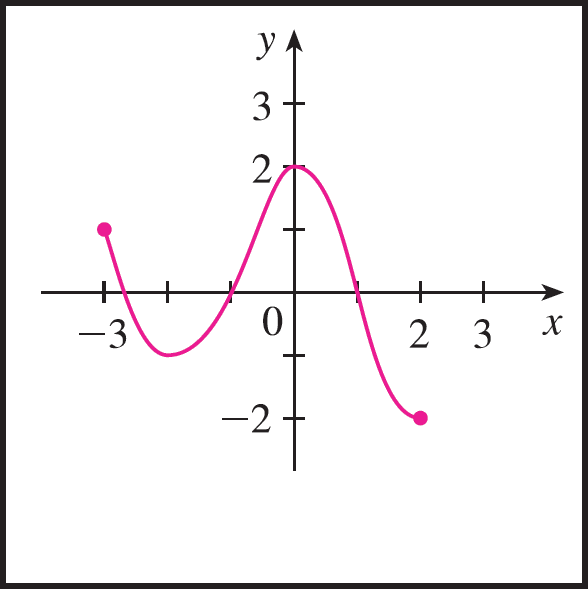
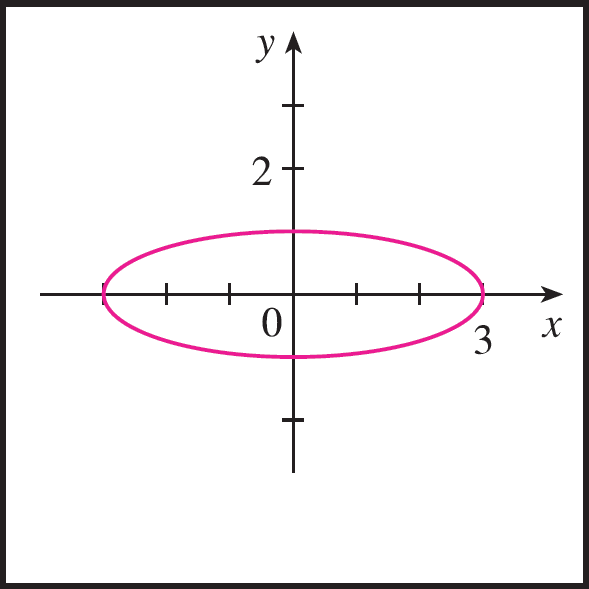
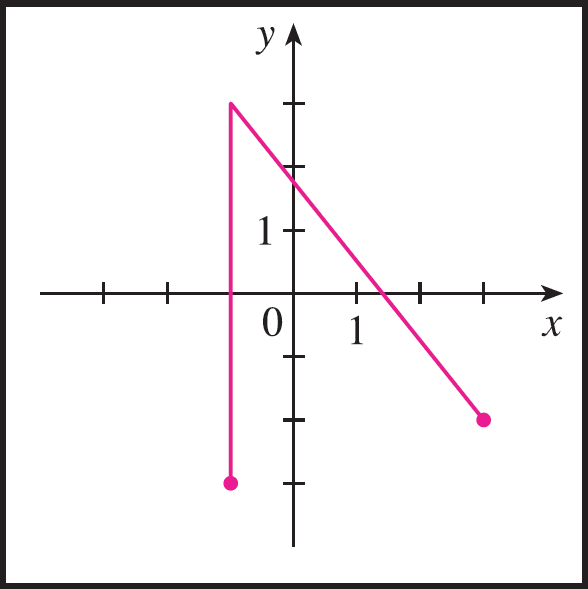
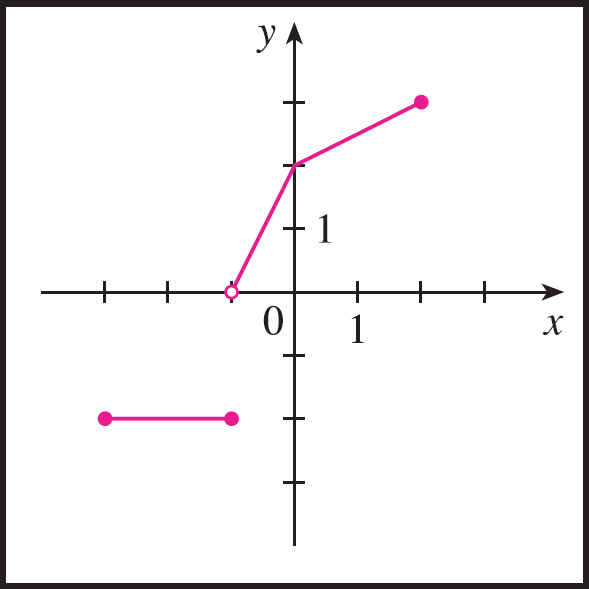
Fig 1 (da esquerda para a direita): Sim, a curva é gráfico de uma função que depende de $x$. O domínio da função é o conjunto $[-3,2]$ e sua imagem é o conjunto $[-2,2]$.
Fig 2: Não, a curva não é gráfico de uma função que depende de $x$, pois a reta vertical $x=0$ intersecta a curva em dois pontos. Na verdade, qualquer reta vertical $x=k$, onde $-3<k<3$ também intersecta a curva em dois pontos.
Fig 3: Não, a curva não é gráfico de uma função que depende de x, pois a reta $x=-1$ intersecta a curva em mais de um ponto (na verdade, em infinitos pontos).
Fig 4: Sim, a curva é gráfico de um função que depende de x. O domínio da função é o conjunto $[-3,2]$ e sua imagem é o conjunto $\{-2\}\cup(0,3]$.
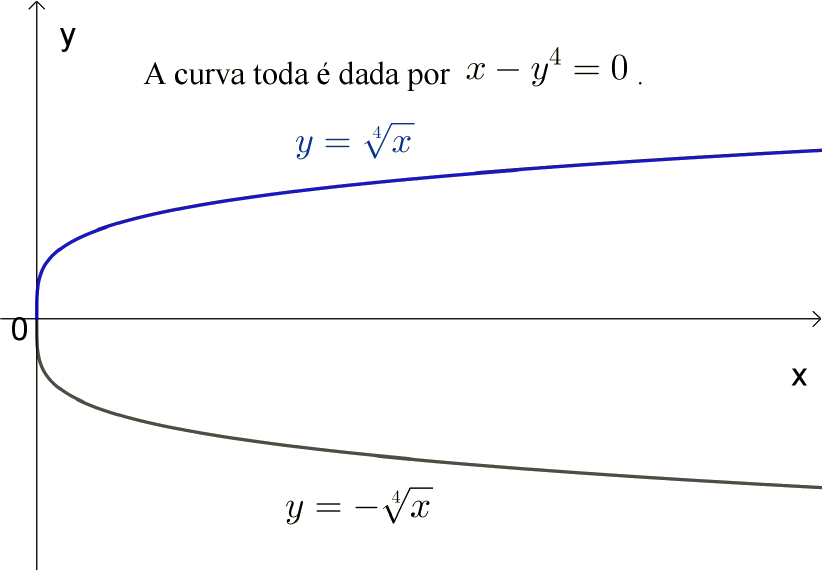
A equação $x-y^4=0$ define uma curva no plano.
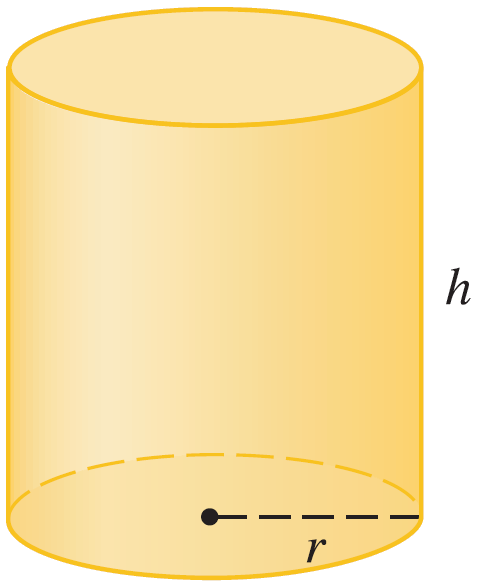
Uma caixa com tampa, em formato de paralelepípedo de base quadrada, deve ter volume $1000\text{ cm}^3$. Determine a área total desta caixa em função da medida $\ell$ de cada aresta da base.
Seja $\text{h}$ a altura da caixa, então seu volume é igual a $h\ell^2$, mas é dado que o volume é igual a $1000$, portanto $1000=h\ell^2 \Rightarrow h=\dfrac{1000}{\ell^2}$. Logo, a área total da caixa em função de $\ell$ é dada por $A=2\ell^2+4\ell h=2\ell^2+4\ell\dfrac{1000}{\ell} \Rightarrow A{\ell}=2\ell^2+\dfrac{4000}{\ell}$, para $\ell>0$.
Um fabricante deseja construir um recipiente, na forma de um cilindro circular reto, que deverá armazenar 1000 $cm^3$ de óleo (o recipiente possui as tampas circulares). O custo de produção do recipiente é medido pela área total do recipiente. Determine uma função real (sua lei de associação e o seu domínio) que expresse o custo de produção em termos do raio $r$ da base circular do cilindro medida em $cm$. Use o GeoGebra para fazer o gráfico da função e, por meio deste gráfico, responda:
É possível gerar um cilindro com custo igual a 500?
É possível gerar um cilindro com custo igual a 1000? De quantas maneiras diferentes?
A área total do recipiente é dada por $A=2zpi r^2$ e precisamos escrever $h$ em função de $r$ para que $A$ seja função somente do raio $r$. Pelo dado problema, $V=\pi r^2 h=1000 \Rightarrow h = \dfrac{1000}{\pi r^2}$ e portanto, temos que
$$A(r)=2\pi r^2+2\pi r\frac{1000}{\pi r^2}=2\pi r^2 + \frac{2000}{r}, r>0$$Gráfico com o GeoGebra:
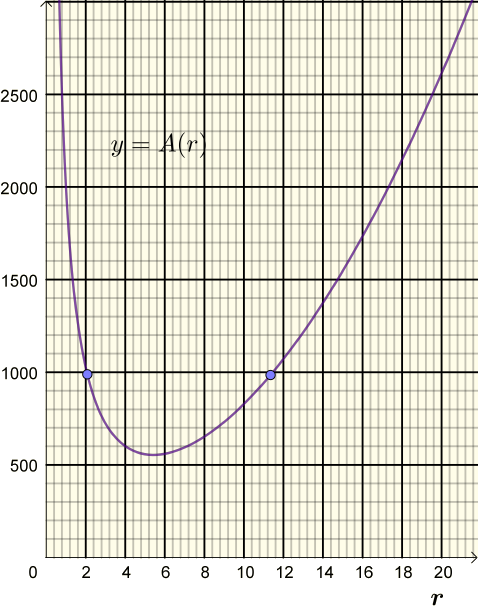
Observe que o custo é medido pela área (quanto via gastar de material). Traçando o gráfico de $A(r)$ no plano $ry$ e a reta $y=500$, observamos que não existe interseção entre os dois, o que significa que $500$ não pertence à imagem de $A$, para $r>0$, ou seja, $A(r)$ é diferente de $500$ para todo $r>0$. Assim, não é possível gerar um cilindro com custo igual a $500$.
Traçando o gráfico de $A(r)$ no plano $ry$ e a reta $y=1000$, observamos que existem 2 interseções entre os dois gráficos, o que significa que há $2$ valores do raio que estão associados ao custo de $1000 (r_{1} \thickapprox 2, r_{2} \thickapprox 11)$. Portanto, há duas maneiras diferentes de construir um recipiente cilíndrico com o custo de $1000$.
Se o ponto $(5, 3)$ estiver no gráfico de uma função par, que outro ponto também deverá estar no gráfico?
Se o ponto $(5, 3)$ estiver no gráfico de uma função ímpar, que outro ponto também deverá estar no gráfico?
$(-5,3)$
$(-5,-3)$
Uma função tem o domínio $[-5, 5]$ e uma parte de seu gráfico é mostrada na figura a seguir.
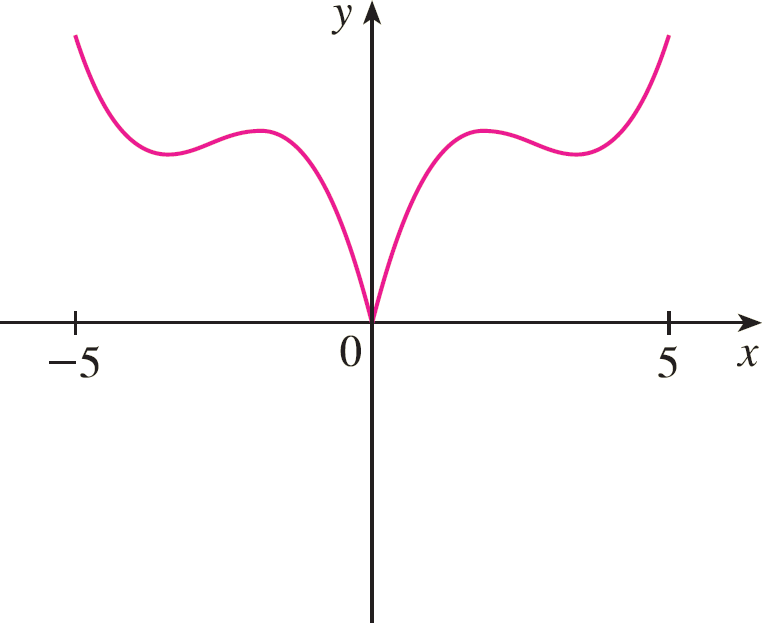
Complete o gráfico de $f$ sabendo que f é uma função par.
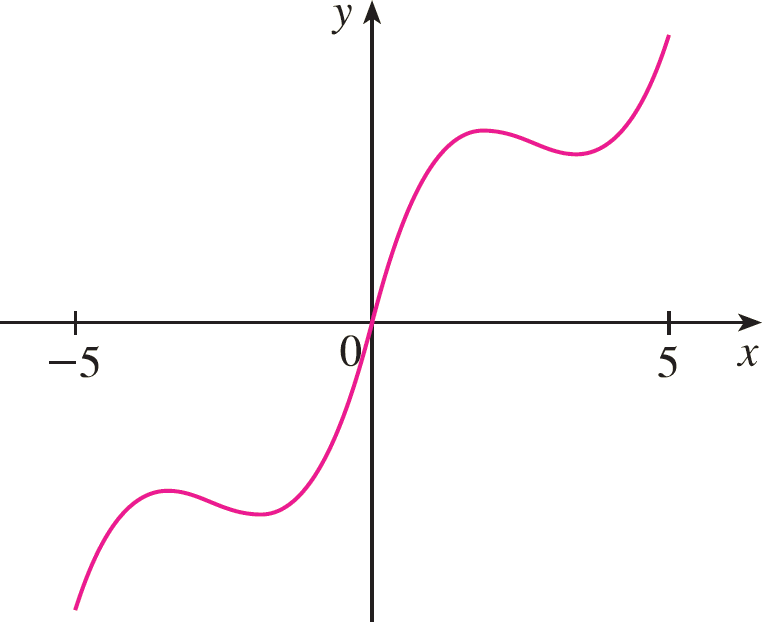
Complete o gráfico de $f$ sabendo que f é uma função ímpar.
Sabendo que $f$ é uma função par, seu gráfico será simétrico em relação ao eixo $y$. Portanto, o gráfico da $f$ fica assim:
Sabendo que $f$ é uma função ímpar, seu gráfico será simétrico em relação à origem. Portanto, o gráfico da $f$ fica assim:
Para cada item a seguir, determine se $f$ é par, ímpar, nenhum dos dois ou os dois ao mesmo tempo.
$y=f(x)=x^4-4x^2$, $x\in\mathbb{R}$
$y=f(x)=x^3-x$, $x\in\mathbb{R}$
$y=f(x)=1$, $x\in\mathbb{R}$
$y=f(x)=3x^3+2x^2+1$, $x\in\mathbb{R}$
$y=f(x)=|x|+x^2+1$, $x\in\mathbb{R}$
$y=f(x)=|x|+x$, $x\in\mathbb{R}$
$f$ é par, pois $f(-x)=(-x)^4(-x)^2=x^4-4x^2=f(x), \forall x \in \mathbb{R}$.
$f$ é ímpar, pois $f(-x)=(-x)^3-(-x)=-x^3-(-x)=-(x^3-x)=-f(x), \forall x \in \mathbb{R}$.
$f$ é par, pois $f(-x)=1=f(x),\forall x \in \mathbb{R}$.
$f$ não é par e nem ímpar. De fato, para $x=-1$, temos $f(-1)=3(-1)^3+2(-1)^2+1=-3+2+1=0$, porém $f(1)=6$. Assim, $f(-1)\neq f(1)=6$ e $f(-1)\neq –f(1)=-6$.
$f$ é par, pois $f(-x) = |-x|+(-x)^2+1=|x|+x^2+1=f(x), \forall x \in \mathbb{R}$.
$f$ não é par e nem ímpar. De fato, para $x=-1$, temos $f(-1)=|-1|+(-1)=1-1=0$, porém $f(1)=2$. Assim, $f(-1)\neq f(1)=2$ e $f(-1)\neq-f(1)=--2$.
Verdadeiro ou falso? Se $f$ é uma função par, então $f$ não é uma função ímpar. Justifique sua resposta!
Falso! Como contraexemplo, considere a função nula $y=f(x)=0$ para todo $x \in \mathbb{R}$. Note que $f$ é par e ímpar ao mesmo tempo. Veja exercício anterior!)
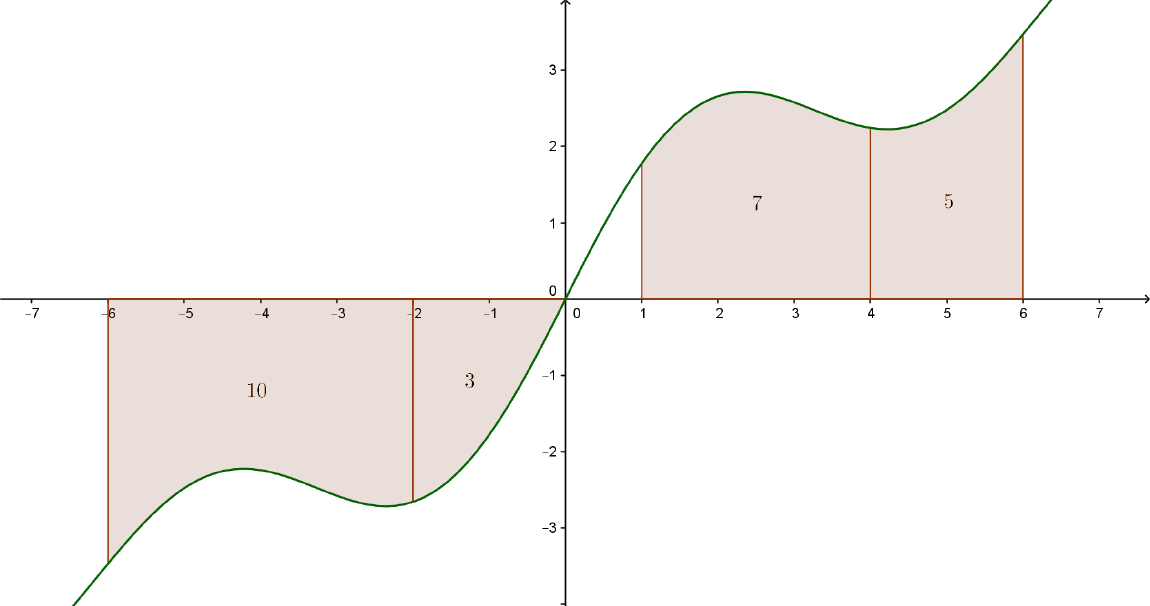
No gráfico da função ímpar $f : \mathbb{R} \rightarrow \mathbb{R}$ representado abaixo, os números representam as áreas destacadas.
Qual é a área representada abaixo?
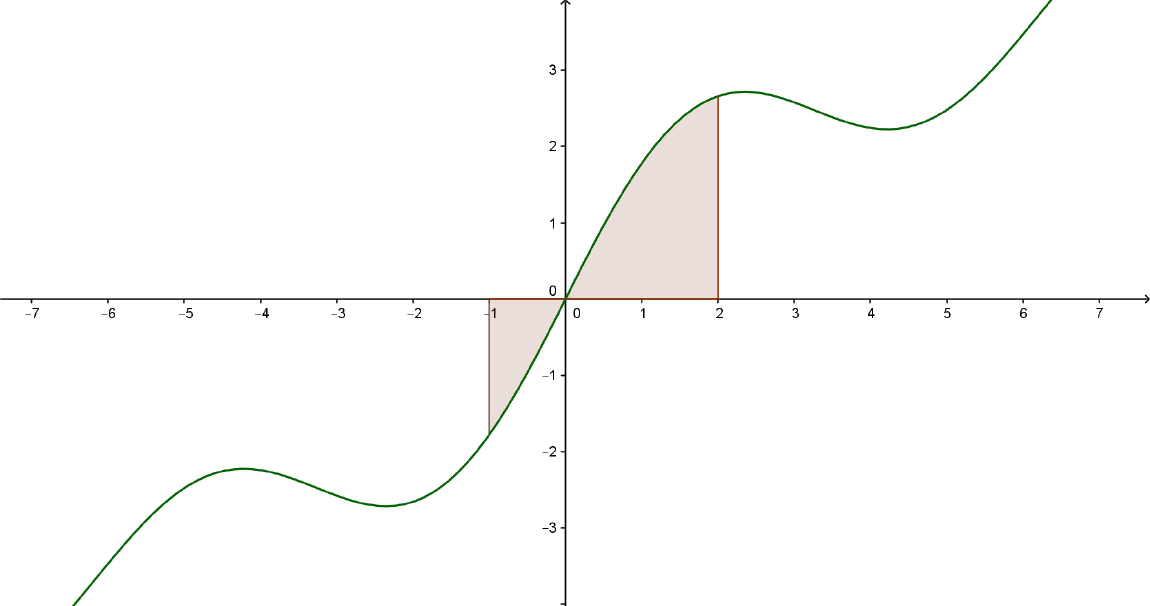
Como a função é ímpar, a área do gráfico entre $-6$ e $0$ será igual à área entre $0$ e $6$, que é $10+3=13$. Assim, como a área entre $1$ e $6$ é $5+7=12$, a área entre $0$ e $1$ será $13-12=1$. Com isso, a área entre -$1$ e $0$ será $1$. A área entre $0$ e $2$ será igual a área entre $-2$ e $0$, que é $3$, portanto a área da figura será igual à soma $1+3=4$.
Diga se cada uma das sentenças abaixo é verdadeira ou falsa.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é par e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f + g$ é par.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f + g$ é par.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f + g$ é ímpar.
Falsa. Podemos usar como contraexemplo $f(x)=2$, $g(x)=x$, a soma $f+g$ não é par. Basta ver que $(f+g)=(-2)=0$ e $(f+g)(2)=4$.
Falsa. Podemos usar como contraexemplo a função constante igual a zero $f(x)=0$ $g(x)=x$, a soma $(f+g)(x)=x$ não é par.
Verdadeira. De fato, $(f+g)(-x)=f(-x)+g(-x)=-f(x)-g(x)=-(f(x)+g(x))=-(f+g)(x), \forall x\in\mathbb{R}$.
Diga se cada uma das sentenças abaixo é verdadeira ou falsa.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é par e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f \cdot g$ é par.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é par e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f \cdot g$ é ímpar.
Se $f : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar e $g : \mathbb{R} \rightarrow \mathbb{R}$ é ímpar, então $f \cdot g$ é par.
Falsa. Tome $f(x)=1$ e $g(x)=x^3$, então o produto $f(x)\cdot g(x)=x^3, \forall x\in\mathbb{R}$, não sendo par.
Verdadeira. De fato, $(f\cdot g)(-x)=f(-x)\cdot g(-x)=f(x)(-g(x))=-f(x)\cdot g(x)=-(f\cdot g)(x), \forall x\in\mathbb{R}$, pois $f$ é par e $g$ é ímpar.
Verdadeira. $(f\cdot g)(-x)=f(-x)\cdot g(-x)=(-f(x))\cdot(-g(x))=f(x)\cdot g(x)=(f\cdot g)(x), \forall x\in\mathbb{R}$, pois $f$ e $g$ são ímpares.
Seja $f : \mathbb{R} \rightarrow \mathbb{R}$ uma função real qualquer. Defina:
$g(x)=\displaystyle \frac{f(x)+f(-x)}{2}$ e $h(x)=\displaystyle \frac{f(x)-f(-x)}{2}$
Mostre que $f=g+h$, que $g$ é uma função par e que $h$ é uma função ímpar.
Determine as funções $g$ e $h$ para o caso em que $f$ é uma função par.
Determine as funções $g$ e $h$ para o caso em que $f$ é uma função ímpar.
Somando
$$g(x)+h(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}=f(x), \forall x\in\mathbb{R}.$$Note que,
$$g(x)=\frac{f(-x)+f(-(-x))}{2}=\frac{f(-x)-f(x)}{2}=g(x), \forall x\in\mathbb{R}.$$Portanto, $g$ é par. Analogamente,
$$h(-x)=\frac{f(-x)-f(-(-x))}{2}=\frac{f(-x)-f(x)}{2}=-h(x), \forall x\in\mathbb{R},$$o que mostra que $h$ é ímpar.
Quando a $f$ é par, temos que a $g$ será a própria $f$ e $h$ será nula.
Quando a $f$ é ímpar, temos que a $h$ será a própria $f$ e $g$ será nula.
Sabemos a imagem de alguns pontos das funções $f$ e $g$ conforme a tabela abaixo:
| $x$ | $-2$ | $-1$ | $1$ | $2$ | $3$ | $5$ |
| $f(x)$ | $2$ | $1$ | $0$ | $2$ | $-1$ | $-1$ |
| $g(x)$ | $2$ | $5$ | $3$ | $-2$ | $0$ | $1$ |
Calcule, se possível, ($f \circ g)(2)$, $(f \circ g)(3)$, $(g \circ f)(5)$, $(f \circ f)(-2)$, $(g \circ g)(5)$.
$(f\circ g)(2)=2$, não dá para determinar $(f\circ g)(3)$ com as informações dadas, $(g\circ f)(5)=5$, $(f\circ f)(-2)=2$, $(g\circ g)(5)=3$.
Sejam $f(x)=5x-2$ e $g(x)=x^2+f(x)$. Calcule $(f \circ g)(2)$.
$f(g(2))=f(4+f(2))=f(4+8)=f(12)=58$
Para cada um dos itens abaixo calcule $(f \circ g)(x)$ e o $\mathrm{D}(f \circ g)$.
$f(x)=x^2-2x-1$ e $g(x)=x+1$;
$f(x)=\sqrt{x-2}$ e $g(x)=x^2-2$;
$f(x)=\sqrt[3]{x+5}$ e $g(x)=x^3-5$;
Considere uma função $f : [0,+\infty) \rightarrow \mathbb{R}$ tal que $f(x) > 5$ se, e somente se, $x>3$.
Determine o domínio da função definida por $g(x)=f(x^2-1)$
Determine o domínio da função definida por $h(x)=\sqrt{5-g(x)}$
Como $\mathrm{D}(f)=[0,+\infty)$, $x$ deve ser, tal que $x^2-1\geq0$, portanto devemos ter $x\in(-\infty,-1]\cup[1,+\infty)$. Logo $\mathrm{D}(g)=[-\infty,-1)\cup[1,+\infty)$.
Devemos ter $x\in \mathrm{D}(g)$ e $5-g(x)\geq0 \iff 5-f(x^2-1)\geq0 \iff f(x^2-1)\leq5 \iff x^2-1\leq3 \iff x^2-4\leq0 \iff -2\leq x \leq 2$. Assim, pelo item anterior, $x\in \mathrm{D}(g)\cap[-2,2]=[-2,-1]\cup[1,2]$.
Na figura abaixo está representado o gráfico da função $f : \mathbb{R} \rightarrow \mathbb{R}$ definida por $(x)=-3\mathrm{sen}(2x)$. Quais são as coordenadas dos pontos $A$ e $B$.
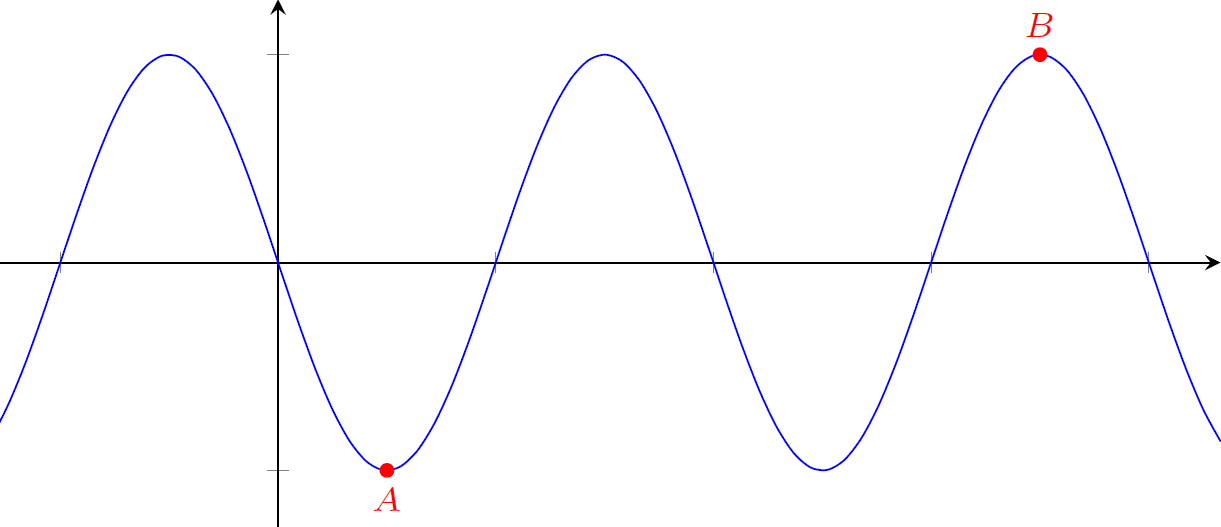
Primeira solução: O ponto $A$ está associado à imagem $-3$ da função e ocorre no menor valor positivo de $x$, mas $-3\mathrm{sen}(2x)=-3$ quando $2x=\frac{\pi}{2}+2k\pi \iff x=\frac{\pi}{4}+k\pi$. Portanto, ocorre quando $k=0$, assim $A=(\frac{\pi}{4},-3)$. O ponto $B$ está associado ao segundo valor positivo de $x$ onde a imagem da função é igual a $3$, mas $-3\mathrm{sen}(2x)=3$ quando $2x=\frac{3\pi}{2}+2k\pi \iff x=\frac{3\pi}{4}+k\pi$. Portanto, ocorre quando $k=1$, assim $B=(\frac{7\pi}{4},3)$.
Segunda solução: O ponto $A$ é resultado das transformações do ponto $(\frac{\pi}{2},1)$ sobreo o gráfico de $y=\mathrm{sen}(x)$. Fazendo uma compressão horizontal de um fator $2$, temos $(\frac{\pi}{4},1)$, com alongamento vertical de um fator $3$, obtemos $(\frac{\pi}{4},3)$. Finalmente, refletindo em torno do eixo $x$, chegamos ao ponto $A=(\frac{\pi}{4},-3)$. O ponto $B$ é resultado das transformações do ponto $(\frac{7\pi}{2},-1)$ sobre o gráfico de $y=\mathrm{sen}(x)$. Seguindo as mesmas transformações anteriores, chegamos a $B=(\frac{7\pi}{4},-3)$.
O ponto $(2,\pi$) pertence ao gráfico de $y=f(x)$. Indique as coordenadas do ponto correspondente, após fazermos a tranformação $y=|2f(x + 5)-10|$.
A partir do gráfico da $f$ foram feitas as seguintes transformações: translação de $5$ unidades para a esquerda; alongamento vertical de um fator $2$; translação vertical de $10$ unidades para baixo; Modulação (nessa ordem). Assim, aplicadno essas transformações ao ponto $(2,\pi)$ obtemos $(-3,\pi)\rightarrow(-3,2\pi)\rightarrow(-3,2\pi-10)\rightarrow(-3,10-2\pi)$, pois $|2\pi-10|=10-2\pi$. O ponto correspondente é $(-3,10-2\pi)$.
A figura abaixo representa o gráfico da função $g$. Faça um esboço do gráfico da função $y=g(2x)$.
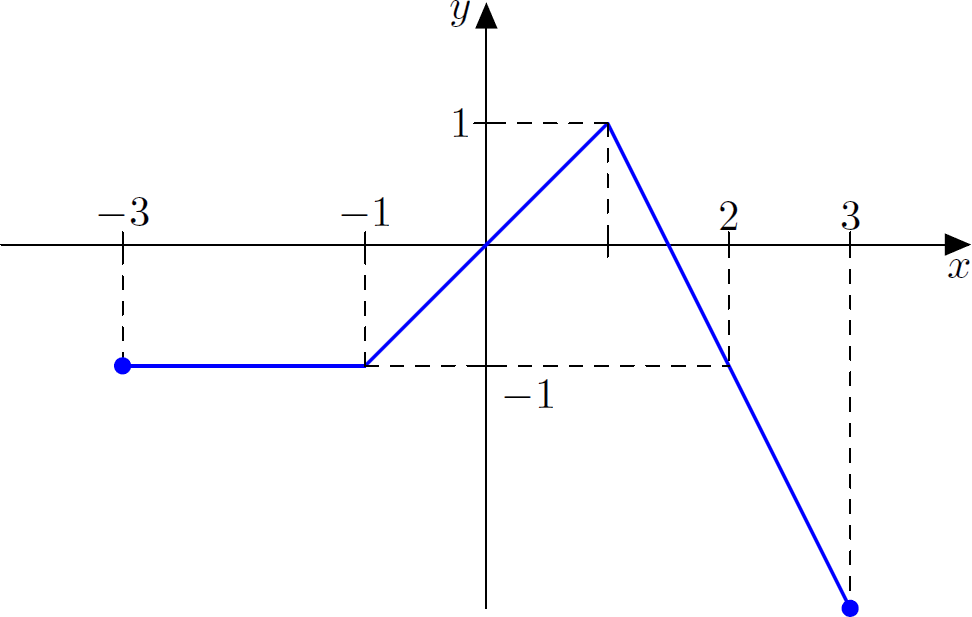
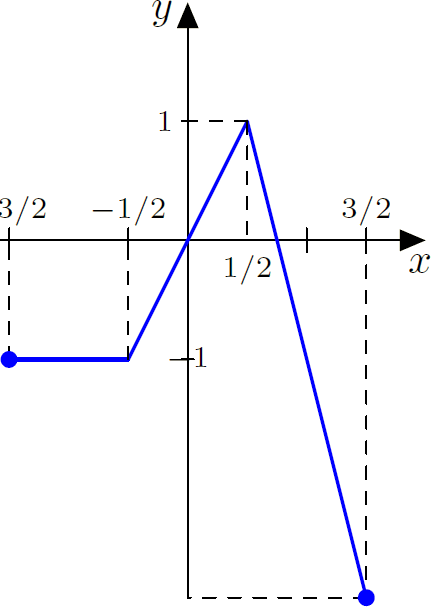
O gráfico de $y=g(2x)$ é obtido fazendo no gráfico da $g$ uma compressão horizontal de um fator $2$:
Faça um esboço dos gráficos das funções abaixo, a partir dos gráfico da função $f(x)=e^x$, $x\in \mathbb{R}$.
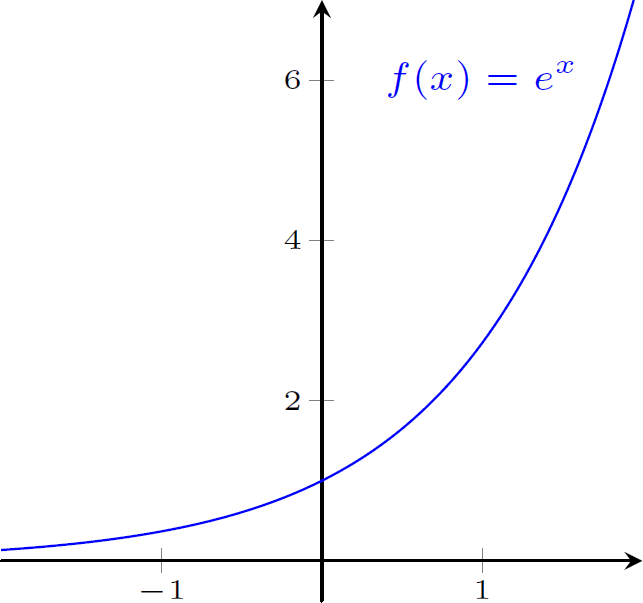
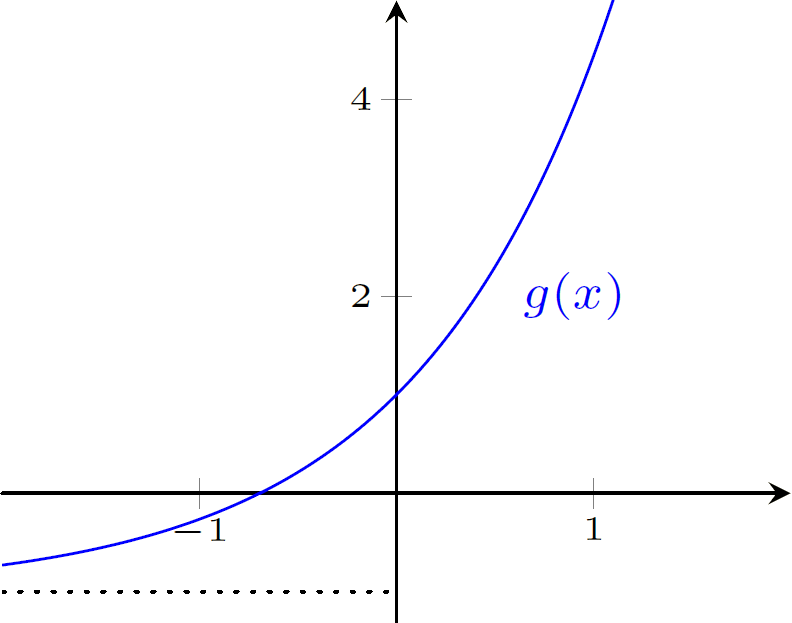
$g(x)=-1+2e^x$
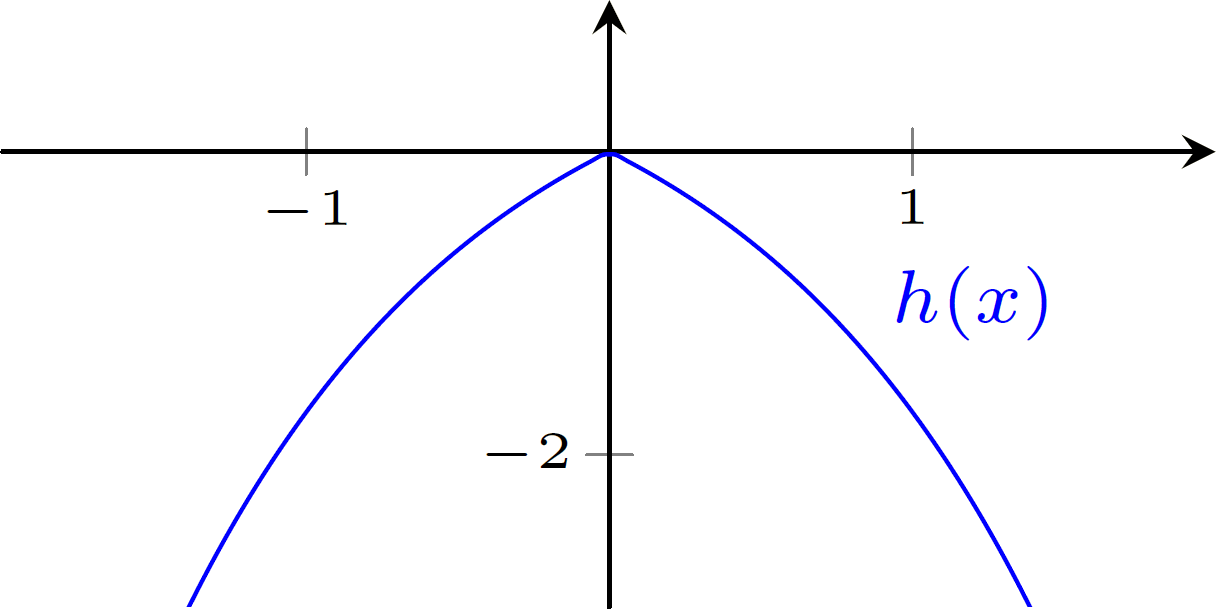
$h(x)=1-e^{|x|}$
Fazemos um alongamento vertical de um fator $2$ (obtemos $y=2e^x$), seguido de uma translação verticla de $1$ unidade para baixo (obtemos $y=2e^x-1$):
A exponencial é composta com módulo de $x$ (nesse passo, a parte do gráfico de $e^x$, para $x\geq0$ é refletida em torno do eixo $y$ e juntando, obtemos o gráfico de $y=e^{|x|}$), finalmente aplicamos uma translação vertical de $1$ unidade para cima (obtemos $y=1-e^{|x|}$).
Considere a função $f(x)=\sqrt{x}$, $x \geq 0$. Se deslocarmos o gráfico de $f$ três unidades para a esquerda, uma unidade para cima e refletirmos em relação ao eixo $y$, obtemos o gráfico da função $g$. Qual a expressão de $g$?
Seguindo os passos na ordem dada no enunciado, temos $y=f(x+3)=\sqrt{x+3}\rightarrow y=\sqrt{x+3}+1\rightarrow g(x)=1+\sqrt{3-x}$. Logo, $g(x)=1+\sqrt{3-x},x\leq3$.