
Vamos considerar uma função real $f$ com domínio em algum subconjunto $D$ de $\mathbb R$. é possível que a derivada exista para alguns valores $x \in D$, mas não exista em outros. Vamos analisar alguns casos em que isso acontece.
Descontinuidades
Já vimos que sempre que a derivada existe em $x_0$, a função é contínua em $x_0$. Assim, em todos os valores em que a função é descontínua, sabemos que a derivada não existe. A figura que veremos tem o gráfico da seguinte função:
$$f(x) = \left\{\begin{array}{lll}2x-1 & \mbox{se} & x \geqslant 1, \\2x+1 & \mbox{se} & x < 1.\end{array}\right.$$
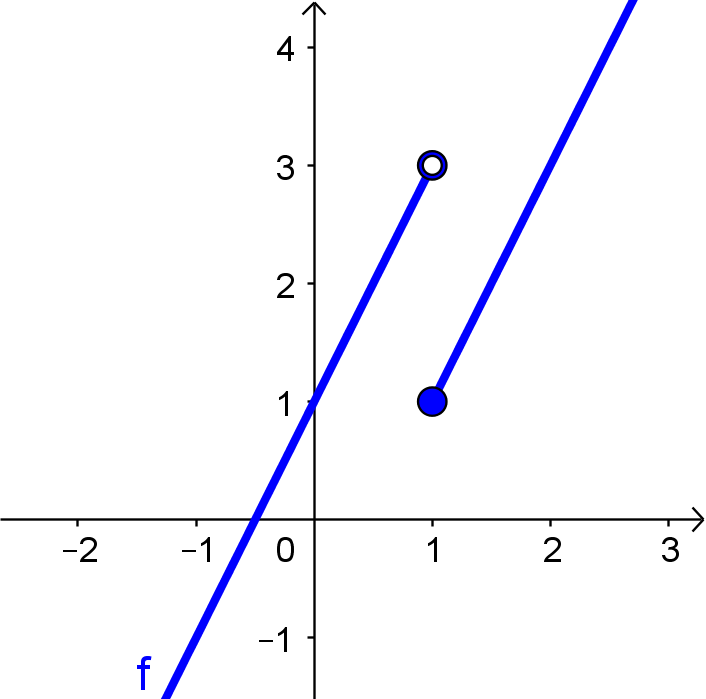
Não é possível determinar uma reta tangente em $x=1$.
Observe que, se olharmos à direita de $x=1$, podemos definir uma tangente. Do mesmo modo, olhando à esquerda de $x=1$, também é possível definir uma tangente. Nesse exemplo, inclusive, as "tangentes" têm a mesma direção à direita e a esquerda mas, a derivada não existe.
Esse exemplo induz um conceito que, às vezes, é usado: derivada à esquerda e derivada à direita.
Dado um ponto $x_0$ no domínio de uma função $f$, podemos definir a derivada em $x_0$ pela esquerda como:
$$f'_{-}({x_0}) = \lim_{x \to {x_0}^-} \frac{f(x) - f(x_0)}{x-x_0}.$$A derivada pela direita (ou à direita) é definida de modo análogo, tomando o limite pela direita, isto é:
$$f'_{+}({x_0}) = \lim_{x \to {x_0}^+} \frac{f(x) - f(x_0)}{x-x_0}.$$Quando a função é contínua mas a derivada não existe.
Observando os pontos $x=0$ e $x=A$ na Figura abaixo , temos dois exemplos típicos de pontos aonde a derivada não existe. No caso $x=0$ é possível ver que a tangente ao gráfico da função é o próprio eixo $\hat{y}$ que tem uma inclinação infinita. Portanto, não é possível descrever a tangente como um polinômio de grau $1$. No caso $x=A$ existe uma tangente à direita e outra, diferente, à esquerda, de modo que a derivada não existe.

Exemplo de função contínua que não tem derivada em $x=0$ e $x=A$.