
Abaixo, vamos descrever uma situação, para o caso particular de televisões, mas que fabricantes, de um modo geral, vivenciam.
Um fabricante de televisões possui uma demanda de aparelhos, em função do preço $x$, dada por $-3x+6.500$ (Exercício 6.9 de expressões do primeiro grau). Supondo que toda a demanda seja vendida, teremos uma receita de $-3x^2+6.500x$ (receita $=$ quantidade vendida $\times$ o preço de venda). Levando-se em conta que o custo de fabricação de cada TV é de R\($\)1.000,00, o custo total das TVs vendidas (toda a demanda) é de $1.000(-3x+6.500)=-3.000x+6.500.000$. Desta forma, o lucro $y$ obtido com a venda das TVs é dado por (lucro $=$ receita $-$ custo)
Expressões como a da lucro obtida acima são chamadas de expressões do segundo grau.
Observe no applet acima a variação do lucro $y$ em função do preço $x$. Aproveite para pensar nas seguintes perguntas:
Uma expressão do segundo grau é do tipo
\begin{eqnarray}y=ax^2+bx+c,\end{eqnarray}com $x \in \mathbb{R}$, onde $a$, $b$ e $c$ são constantes reais, com $a\not = 0$. Note que se $a=0$, temos uma expressão do primeiro grau, estudada anteriormente. A representação de $y=ax^2+bx+c$, $x \in \mathbb{R}$, no plano cartesiano, dada pelos pares ordenados $(x,ax^2+bx+c)$, ou seja, o gráfico de uma expressão do segundo grau é uma curva chamada de parábola, que intersecta o eixo $y$ no ponto $(0,c)$, cuja concavidade é para cima ($\cup$), quando $a>0$ e é para baixo ($\cap$), quando $a<0$. Observe os exemplos a seguir:
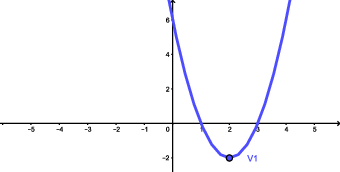
Parábola (i): $y=2x^2-8x+6$
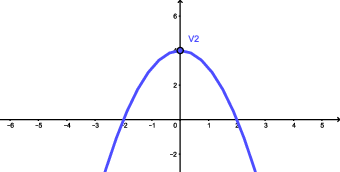
Parábola (ii): $y=4-x^2$
Parábola (iii): $y=x^2-2x+2$

Parábola (iv): $y=-x^2+4x-4$
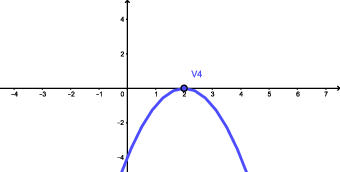
Nos exemplos de parábolas acima, marcamos os pontos importantes $V_1$, $V_2$, $V_3$ e $V_4$, que são os vértices das parábolas. A notação usual para a abscissa e a ordenada do vértice $V$ de uma parábola é, respectivamente, $x_v$ e $y_v$. Assim , temos que $V=(x_v,y_v)$. Nas parábolas (i) e (iii), como o coeficiente do termo de segundo grau é positivo, i.e. $a>0$, a ordenada do vértice, $y_v$, corresponde ao menor valor que a expressão quadrática assume em toda a reta real. Já nas parábolas (ii) e (iv), sendo $a<0$, a ordenada do vértice, $y_v$, corresponde ao maior valor que a expressão quadrática assume em toda a reta real.
Observe que nas parábolas (i), (ii) e (iv) há interseção da parábola com o eixo $x$, mas, na parábola (iii), não existe interseção da parábola com o eixo $x$. Em todos os exemplos, entretanto, há interseção com o eixo $y$.
As raízes da equação $ax^2+bx+c=0$ está entre os assuntos mais lembrados da Matemática do Ensino Médio. Imediatamente nos vem à mente a clássica expressão $\dfrac{-b\pm \sqrt{\Delta}}{2a}$, que, como tantas outras, faz parte do nosso repertório de expressões lembradas mas, não necessariamente entendidas.
Esta expressão é parte da famosa ``Fórmula de Bhaskara'' para solução da equação do segundo grau. Esperamos deixar claro a importância do ``$\Delta$'', $\Delta=b^2-4ac$, associado a uma expressão do segundo grau em relação ao estudo das raízes (interseções com o eixo $x$). Abaixo apresentaremos a igualdade que permite concluir a fórmula das raízes da equação $ax^2+bx+c=0$ e, se você tiver curiosidade de saber como aparece esse ``tal delta'', não deixe de ler a seção ``Sobre a Fórmula de Bhaskara''.
Através de umas manipulações algébricas que são feitas em detalhes na seção referida acima, temos que
\begin{eqnarray} \tag{1}y=ax^2+bx+c=a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a},\end{eqnarray}onde $\Delta=b^2 - 4ac$, de modo que
\[ax^2+bx+c=0 \Leftrightarrow \left(x + \frac{b}{2a}\right)^2 = \frac{\Delta}{4a^2}.\]Portanto, temos que a equação $ax^2+bx+c=0$:
possui duas soluções reais distintas se, e somente se, $\Delta > 0$, sendo estas
\[x_1 = -\frac{b}{2a} +\dfrac{\sqrt{\Delta}}{2a}= \frac{-b+\sqrt{\Delta}}{2a} \text{ e } x_2 = -\frac{b}{2a} -\dfrac{\sqrt{\Delta}}{2a}= \frac{-b-\sqrt{\Delta}}{2a},\]ou, escrito de forma condensada
\[x = -\frac{b}{2a} \pm\dfrac{\sqrt{\Delta}}{2a}= \frac{-b\pm\sqrt{\Delta}}{2a};\]possui duas soluções reais iguais se, e somente se, $\Delta = 0$, sendo esta
\[x = -\frac{b}{2a};\]não possui soluções reais se, e somente se, $\Delta < 0$, pois um número real ao quadrado é sempre positivo ou nulo (quando o próprio número é zero).
Aproveite o applet abaixo para visualizar a variação do número de raízes em função do sinal de $\Delta$ alterando os valores de $a$, $b$ e $c$.
Encontre as raízes, caso existam, das equações exemplificadas pelas parábolas de (i) a (iv) dadas anteriormente, ou seja, das equações abaixo.
Portanto, a equação $x^2-3x+2=0$ possui duas raízes reais distintas, sendo elas,
\[x_1 = \dfrac{-(-8)+\sqrt{16}}{2(2)}=\dfrac{8+4}{4} =\dfrac{12}{4}=3\]e
\[x_2 = \dfrac{-(-8)-\sqrt{16}}{2(2)}=\dfrac{8-4}{4} =\dfrac{4}{4}=1.\]Portanto, a equação $4-x^2=0$ possui duas raízes reais distintas, sendo elas,
\[x_1 = \dfrac{-(0)+\sqrt{16}}{2(1)}=\dfrac{4}{2} =2\]e
\[x_2 = \dfrac{-(0)-\sqrt{16}}{2(1)}=-\dfrac{4}{2} =-2.\]Você poderia ter resolvido esta igualdade de um outra forma bem simples:
$$4-x^2=0 \Leftrightarrow x^2=4 \Leftrightarrow x-2 \text{ ou } x=-2.$$Portanto, a equação $x^2-2x+2=0$ não possui raízes reais .
Portanto, a equação $-x^2+4x-40$ possui duas raízes reais iguais, sendo elas,
\[x_1 = x_2 = \dfrac{-(4)}{2(-1)}=\dfrac{-4}{-2} =2\]O vértice de uma parábola é dado por $V=(x_v,y_v )=\left(-\dfrac{b}{2a},-\dfrac{\Delta}{4a}\right)$. Mas, o que esse ponto tem de especial a ponto de ser ressaltado?
Vamos supor primeiro que $a>0$ e voltar à igualdade 1 para respondermos essa pergunta. Observe que
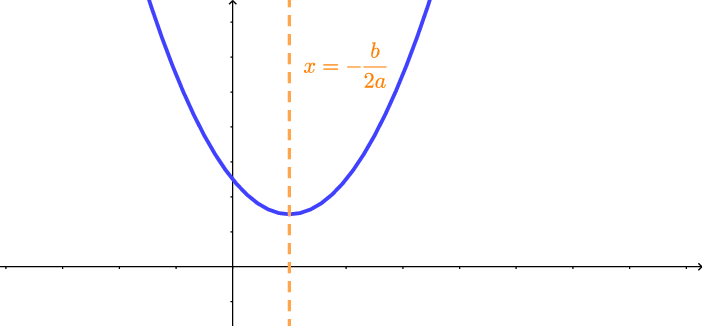
$$y=a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a}$$assumirá o valor mínimo quando $(x+b/2a)^2=0$, pois esse termo, por ser o quadrado de um número real, é nulo ou positivo. Logo, se $a>0$, $x_v=-\dfrac{b}{2a}$ é a abscissa do ponto onde a ordenada $y$ tem o valor mínimo, a saber, $-\dfrac{\Delta}{4a}$. Na próxima seção, ao estudarmos parábolas, veremos que se $a>0$, a parábola possui concavidade voltada para cima. Desta forma, verificaremos geometricamente que é no vértice que se dá o menor valor da ordenada $y$ da parábola.
De forma análoga, se $a<0$, temos que
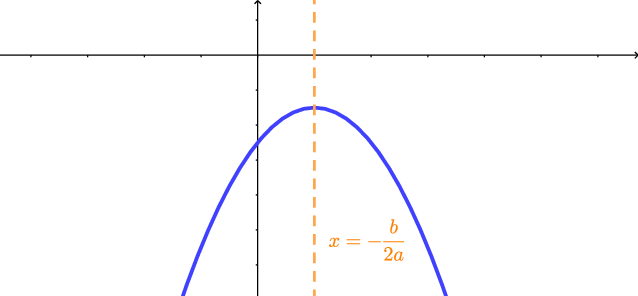
assumirá o valor máximo quando $(x+b/2a)^2=0$, pois esse termo é nulo ou positivo. Logo, se $a<0$, $x_v=-\dfrac{b}{2a}$ é a abscissa do ponto onde a ordenada $y$ tem o valor máximo, a saber, $-\dfrac{\Delta}{4a}$. Na próxima seção, ao estudarmos parábolas, veremos que se $a<0$, a parábola possui concavidade voltada para baixo. Desta forma, verificaremos geometricamente que é no vértice que se dá o maior valor da ordenada $y$ da parábola.
Encontre o vértice das parábolas abaixo (parábolas (i), (ii), (iii) e (iv)).
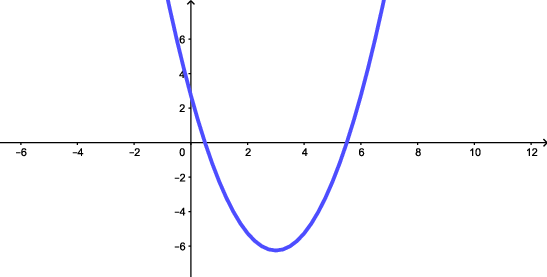
Voltando ao exemplo inicial do fabricante de televisões, determine o lucro máximo que ele pode conseguir e o preço aplicado onde isto ocorre.
Vimos que a expressão do lucro $y$ em função do preço $x$ é dada por,
$$y = -3x^2+9.500x-6.500.000.$$Como nesta expressão do segundo grau, temos $a=-3<0$, conforme observado, $x_v=-\dfrac{b}{2a}$ fornece a abscissa do ponto onde a ordenada $y$ tem o valor máximo e este valor máximo é dado por $y_v=-\dfrac{\Delta}{4a}$.
Desta forma, como $\Delta=(-9.500)^2-4(-3)(-6.500.0000)=12.250.000$, o lucro máximo obtido é de
e ele ocorre quando o preço aplicado é de
$$x=-\dfrac{b}{2a}=-\dfrac{9.500}{2(-3)}=\dfrac{9.500}{6}=\dfrac{4750}{3} \approx 1583,33.$$Observe que com a teoria estudada, você consegue fornecer valores exatos para o lucro máximo e para o preço associado a ele, valores estes, que antes podiam ser dados apenas de forma aproximada pela observação do gráfico do lucro.
Vimos que a representação de $y=ax^2+bx+c$, $x \in \mathbb{R}$, $a$, $b$, $c$ constantes reais e $a \not=0$ , no plano cartesiano, é dada pelos pares ordenados $(x,ax^2+bx+c)$, ou seja, o gráfico de uma expressão do segundo grau é uma curva chamada de parábola, cuja concavidade é para cima ($\cup$), quando $a>0$ e é para baixo ($\cap$), quando $a<0$.
Nesta seção, vamos dividir o esboço de parábolas em seis diferentes casos, dependendo do sinal de $a$ e do sinal de $\Delta$, que, conforme visto, se relaciona com o número de raízes da equação $ax^2+bx+c=0$, ou equivalentemente, com o número de interseções da parábola com o eixo $x$.
Para desenhar uma parábola, temos que determinar a sua concavidade, o seu vértice e onde ela intersecta os eixos coordenados. Observe que a reta dada por $x=x_v$ é o eixo de simetria da parábola. Isto significa que o esboço da parte da parábola para $x>x_v$ é o espelho (reflexo) do esboço da parte da parábola para $x_0$, a parábola possui concavidade voltada para cima e, se $a<0$, a parábola tem concavidade voltada para baixo.
(a) $a>0$: Concavidade para cima
(b) $a<0$: Concavidade para baixo

Note que, quando um ponto $(x,y)$ está sobre o eixo $y$, sua primeira coordenada, ou seja, a abscissa do ponto, é igual a zero. Assim, para determinar os valores $y$ em que a parábola $y=ax^2+bx+c$ intersecta o eixo $y$, fazemos $x=0$, nesta equação. Desta forma, o valor $y$ procurado deve ser a solução de $y=a(0)^2+b(0)+c=0$, ou seja, $y=c$. Portanto, a parábola intersecta o eixo $y$ no ponto $(0,c)$.
Por outro lado, note que, quando um ponto $(x,y)$ está sobre o eixo $x$, sua segunda coordenada, ou seja, a ordenada do ponto, é igual a zero. Assim, para determinar os valores $x$ em que a parábola $y=ax^2+bx+c$ intersecta o eixo $x$, fazemos $y=0$, nesta equação. Desta forma, os valores $x$ procurados devem ser as soluções da equação do segundo grau $ax^2+bx+c=0$, estudadas na seção anterior e dadas pela fórmula de Bhaskara
Conforme visto, de acordo com o valor de $\Delta$, podemos ter três tipos de soluções para a equação $ax^2+bx+c=0$.
Caso 1: $\Delta=b^2-4ac>0$.
Neste caso, a equação $ax^2+bx+c=0$ tem como solução dois valores reais distintos, dados por
\[x_1=\dfrac{-b-\sqrt{\Delta}}{2a} \text{ e } x_2=\dfrac{-b+\sqrt{\Delta}}{2a},\]de modo que a parábola intersecta o eixo $x$ nos pontos $(x_1,0)$ e $(x_2,0)$. Vamos dividir este caso em dois subcasos, em função do sinal de $a$.
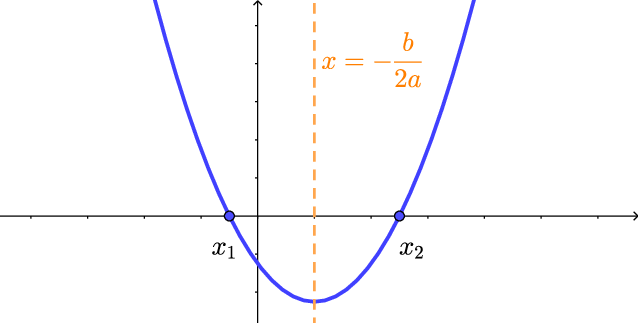
Caso 1a: $\Delta=b^2-4ac>0$ e $a>0$.
Como $a~>~0$, a concavidade da parábola é para cima.
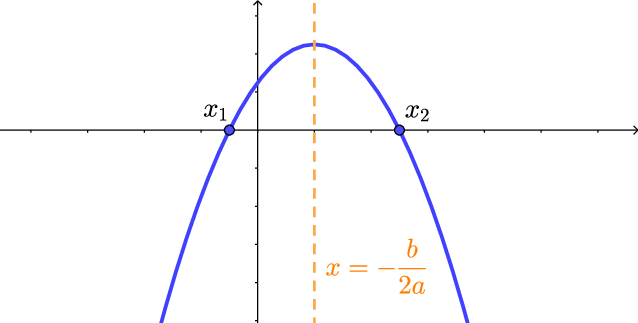
Caso 1b: $\Delta=b^2-4ac>0$ e $a<0$.
Como $a<0$, a concavidade da parábola é para baixo.
Caso 2: $\Delta=b^2-4ac=0$.
Neste caso, a equação $ax^2+bx+c=0$ tem uma única solução, dada por
\[x_1=x_2=-\dfrac{b}{2a}.\]Portanto, a parábola intersecta o eixo $x$ no ponto $(x_1,0)$. Como anteriormente feito, vamos dividir este caso em dois subcasos, em função do sinal de $a$.
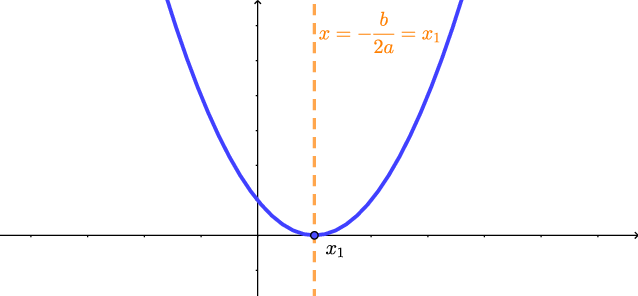
Caso 2a: $\Delta=b^2-4ac=0$ e $a>0$.
Como $a>0$, a concavidade da parábola é para cima.
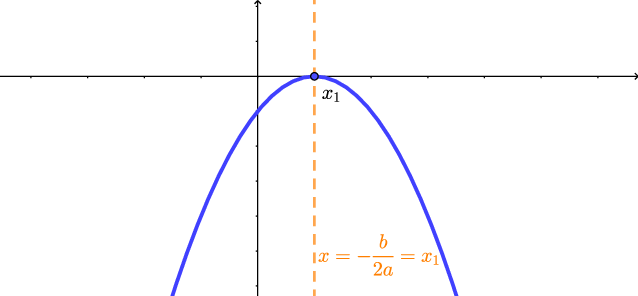
Caso 2b: $\Delta=b^2-4ac=0$ e $a<0$.
Como $a<0$, a concavidade da parábola é para baixo.
Caso 3: $\Delta=b^2-4ac<0$.
Neste caso, a equação $ax^2+bx+c=0$ não possui solução real. Como feito antes, vamos dividir este caso em dois subcasos, em função do sinal de $a$.
Caso 3a: $\Delta=b^2-4ac<0$ e $a>0$.
Como $a>0$, a concavidade da parábola é para cima.
(3b) $\Delta=b^2-4ac<0$ e $a<0$.
Como $a<0$, a concavidade da parábola é para baixo.
Esboce diferentes parábolas alterando os valores de $a$, $b$ e $c$ com o applet abaixo. É bem divertido!
Observe que:
a parábola (i), dada por $y=2x^2-8x+6$ ,se enquadra no Caso (1a), pois $\Delta=16 >0$ e $a=2> 0$: concavidade voltada para cima e com duas interseções com o eixo $x$;
a parábola (ii), dada por $y=4-x^2$, se enquadra no Caso (1b), pois $\Delta=16 >0$ e $a=-1< 0$: concavidade voltada para baixo e com duas interseções com o eixo $x$;
a parábola (iii), dada por $y=x^2-2x+2$, se enquadra no Caso (3a), pois $\Delta =-4<0$ e $a=1> 0$: concavidade voltada para cima e nenhuma interseção com o eixo $x$;
a parábola (iv), dada por $y=-x^2+4x-4$ se enquadra no Caso (2b), pois $\Delta =0$ e $a=-1< 0$: concavidade voltada para baixo e com apenas uma interseção com o eixo $x$.
Voltando ao nosso exemplo inicial, suponha que o fabricante queira saber o intervalo de preços no qual ele pode trabalhar, de forma que obtenha lucro. Observe que obter lucro, significa que a expressão que representa o lucro, que é a expressão $y = -3x^2+9.500x-6.500.000$, deve ser positiva. Desta forma, o que o fabricante deseja saber é quando
$$-3x^2+9.500x-6.500.000>0.$$Análises como a acima são conhecidas como estudo de sinais de expressões e, neste caso, desejamos estudar o sinal de uma expressão do segundo grau. Para fazermos isto, vamos aproveitar nosso conhecimento de parábolas da seção anterior.
Conforme vimos, a representação de $y=ax^2+bx+c$, $x \in \mathbb{R}$, $a$, $b$, $c$ constantes reais e $a \not=0$ , no plano cartesiano, dada pelos pares ordenados $(x,ax^2+bx+c)$, ou seja, o gráfico de uma expressão do 2$^\text{o}$ grau é uma parábola, cuja concavidade é para cima ($\cup$), quando $a>0$ e é para baixo ($\cap$), quando $a<0$ e cuja interseção com o eixo $x$ é regida pelo valor de $\Delta$.
Desta forma, repare que querer determinar os valores de $x$ para os quais $ax^2+bx+c>0$, equivale a descobrir os valores de $x$ para os quais a ordenada $y$ dos pontos da parábola $y=ax^2+bx+c$ é positiva, uma vez que um ponto $(x,y)$ desta parábola é da forma $(x,ax^2+bx+c)$. Agora, repare que os valores de $x$ para os quais a ordenada $y$ da parábola é positiva, são os valores de $x$ correspondentes às partes da parábola que estão acima do eixo $x$. Analogamente, para determinar os valores de $x$ para os quais $ax^2+bx+c<0$ precisamos descobrir os valores de $x$ para os quais a ordenada $y$ dos pontos da parábola $y=ax^2+bx+c$ é negativa, que são os valores de $x$ correspondentes às partes da parábola que estão abaixo do eixo $x$. Lembre-se que você já sabe os valores de $x$ tais que $ax^2+bx+c=0$, que são dados pela fórmula de Bhaskara, quando $\Delta \geq 0$, e que são os pontos da parábola sobre o eixo $x$.
Vamos então dividir o estudo de sinais de uma expressão do segundo grau analisando o valores de $\Delta$ e de $a$, da mesma forma feita no esboço de parábolas da seção anterior.
Caso 1: $\Delta=b^2-4ac>0$.
Neste caso, a equação $ax^2+bx+c=0$ tem como solução dois valores reais distintos, dados por,
\[x_1=\dfrac{-b-\sqrt{\Delta}}{2a} \text{ e } x_2=\dfrac{-b+\sqrt{\Delta}}{2a},\]de modo que a parábola intersecta o eixo $x$ nos pontos $(x_1,0)$ e $(x_2,0)$.
Caso 1a: $\Delta=b^2-4ac>0$ e $a>0$.
Como $a>0$, a concavidade da parábola é para cima. Portanto, a parábola está abaixo do eixo $x$ entre as raízes e acima do eixo $x$, fora. Ou seja,
$y=ax^2+bx+c>0$, para $x<x_1$ ou $x> x_2$.
$y=ax^2+bx+c<0$, para $x_1<x< x_2$.
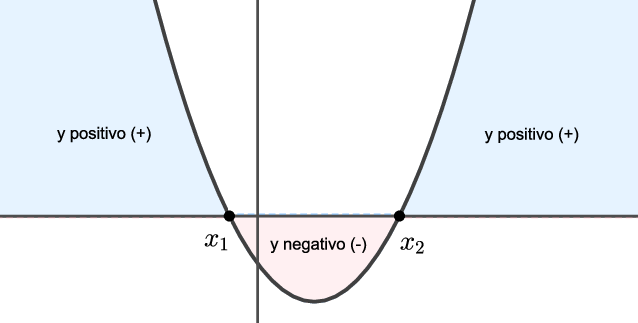
Caso 1b: $\Delta=b^2-4ac>0$ e $a<0$.
Como $a<0$, a concavidade da parábola é para baixo. Portanto, a parábola está acima do eixo $x$ entre as raízes e abaixo do eixo $x$, fora. Ou seja,
$y=ax^2+bx+c>0$, para $x_1<x< x_2.$
$y=ax^2+bx+c<0$, para $x<x_1$ ou $x> x_2.$
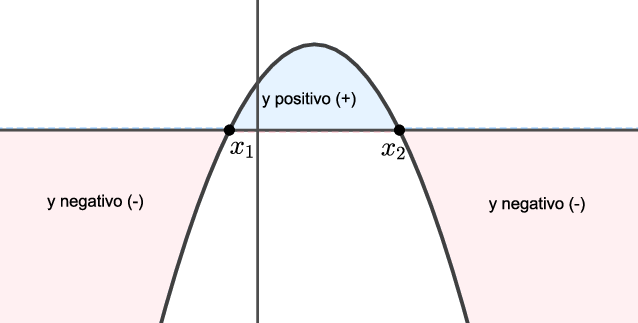
Caso 2: $\Delta=b^2-4ac=0$.
Neste caso, a equação $ax^2+bx+c=0$ tem uma única solução, dada por,
\[x_1=x_2=-\dfrac{b}{2a}.\]Portanto, a parábola intersecta o eixo $x$ no ponto $(x_1,0)$.
Caso 2a: $\Delta=b^2-4ac=0$ e $a>0$.
Como $a>0$, a concavidade da parábola é para cima. Portanto, tirando o ponto $x_1=-\dfrac{b}{2a}$, onde $y=0$ e a parábola ``toca'' o eixo $x$, temos que a parábola está sempre acima do eixo $x$. Ou seja,
$y=ax^2+bx+c>0$, para $x\not =-\dfrac{b}{2a}$.
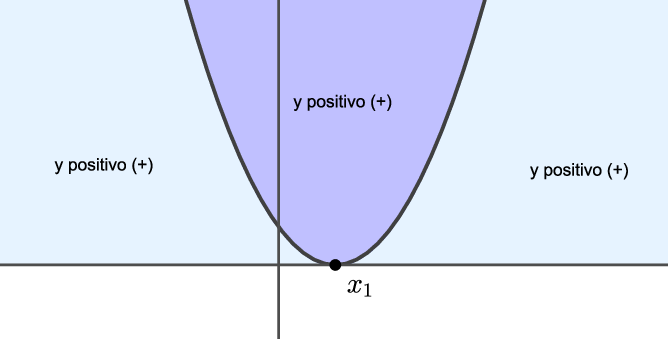
Caso 2b: $\Delta=b^2-4ac=0$ e $a<0$.
Como $a<0$, a concavidade da parábola é para baixo. Portanto, tirando o ponto $x=-\dfrac{b}{2a}$, onde $y=0$ e a parábola ``toca'' o eixo $x$, temos que a parábola está sempre abaixo do eixo $x$. Ou seja,
$y=ax^2+bx+c<0$, para $x\not =-\dfrac{b}{2a}$.

Caso 3: $\Delta=b^2-4ac<0$.
Neste caso, a equação $ax^2+bx+c=0$ não possui solução real.
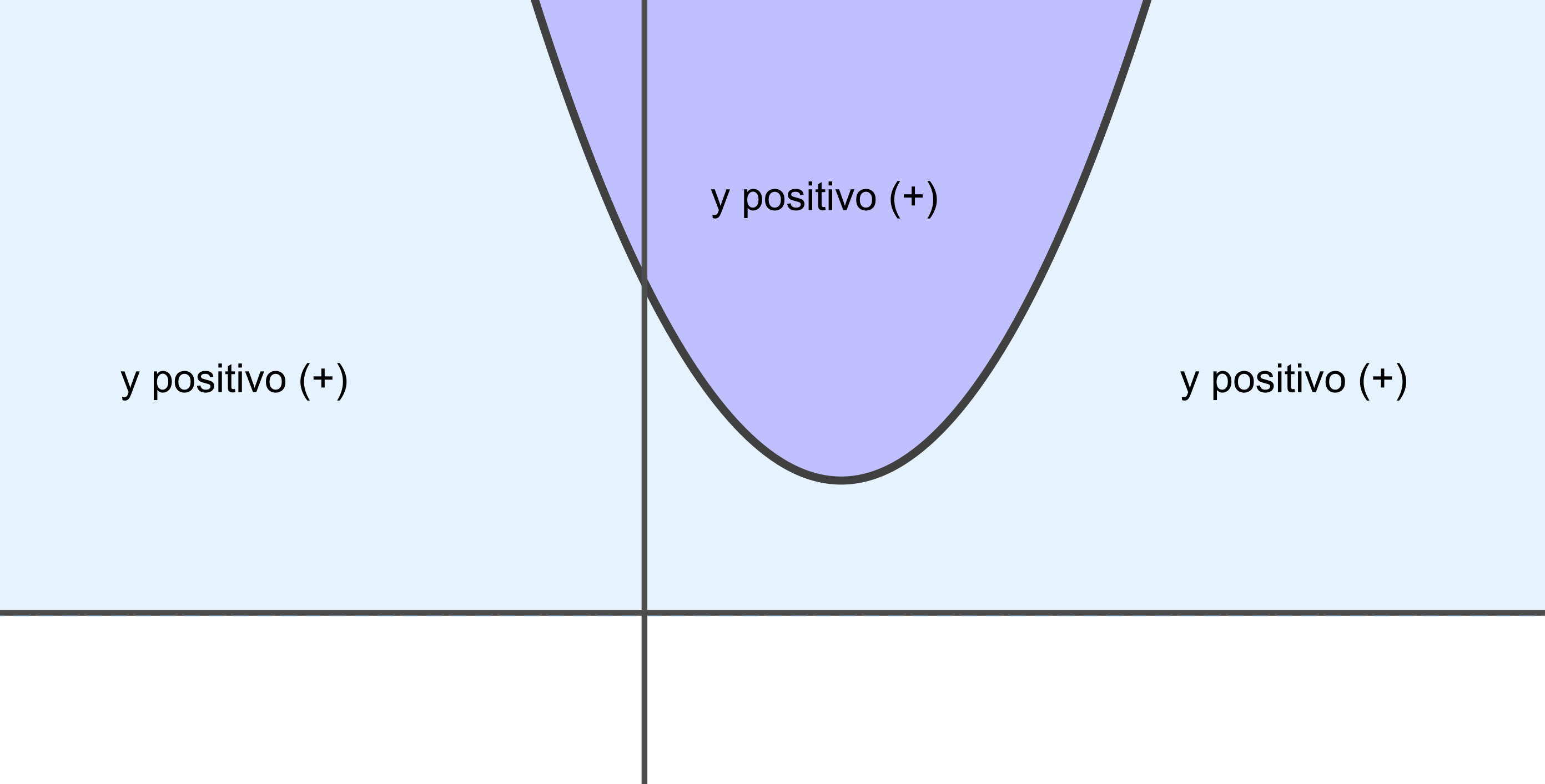
Caso 3a: $\Delta=b^2-4ac<0$ e $a>0$.
Como a equação $ax^2+bx+c=0$ não possui soluções reais, a parábola não intersecta o eixo $x$.
Como $a>0$, a concavidade da parábola é para cima. Portanto, temos que a parábola está sempre acima do eixo $x$ para qualquer valor de $x$. Ou seja,
$y=ax^2+bx+c>0$, para $x\in \mathbb{R}$.
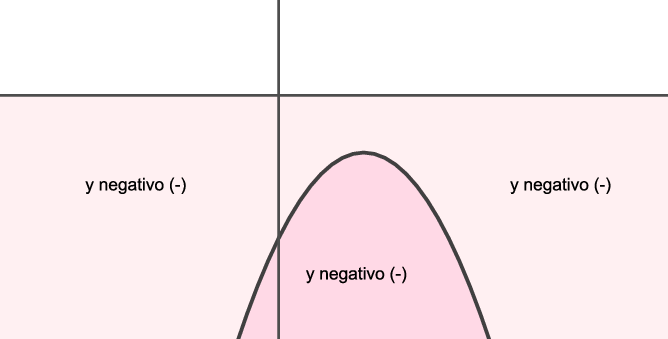
Caso 3b: $\Delta=b^2-4ac<0$ e $a<0$.
Como a equação $ax^2+bx+c=0$ não possui soluções reais, a parábola não intersecta o eixo $x$.
Como $a<0$, a concavidade da parábola é para baixo. Portanto, temos que a parábola está sempre abaixo do eixo $x$ para qualquer valor de $x$. Ou seja,
$y=ax^2+bx+c<0$, para $x\in \mathbb{R}$.
De posse dos conhecimentos adquidos anteriormente, vamos resolver o problema do exemplo inicial e determinar, de forma exata e não somente aproximada, o intervalo de preços no qual o fabricante possui lucro. Ou seja, vamos determinar para que valores de $x$, tem-se $y = -3x^2+9.500x-6.500.000>0$. Neste caso, como $\Delta=(-9.500)^2-4(-3)(6.500.0000)=12.250.000>0$, temos que a equação $-3x^2+9.500x-6.500.000=0$ possui duas raízes reais distintas. São elas,
\[x_1=\dfrac{-9.500+\sqrt{12.250.000}}{2.(-3)} =\dfrac{-9.500+3.500}{-6}=\dfrac{-6.000}{-6}=1.000\]e
de modo que a parábola intersecta o eixo $x$ nos pontos $(1.000,0)$ e $\left(3.250,0\right)$.
Como $a=-3<0$, a parábola possui concavidade voltada para baixo e, portanto, o valor do lucro $y$ será positivo quando o preço $x$ estiver entre as raízes. Sendo assim, temos que
Observe que lucro negativo significa prejuízo e, portanto, deve ser evitado!
Vamos aproveitar para verificar os sinais das expressões dadas pelas parábolas de (i) a (iv):
a parábola (i), dada por $y=2x^2-8x+6$, se enquadra no Caso (1a): possui duas raízes reais distintas, a saber, $x_1=3$ e $x_2=1$, e tem $a=2> 0$. Portanto, a ordenada $y$ é negativa entre as raízes e positiva, fora. Ou seja,
\begin{eqnarray*}y=2x^2-8x+6>0 &\Leftrightarrow& x<1 \text{ ou } x>3; \\y=2x^2-8x+6<0 &\Leftrightarrow& 1<x<3; \\y=2x^2-8x+6=0 &\Leftrightarrow& x=1 \text{ ou } x=3;\end{eqnarray*}a parábola (ii), dada por $y=4-x^2$, se enquadra no Caso (1b): possui duas raízes reais distintas, a saber, $x_1=2$ e $x_2=-2$, e tem $a=-1< 0$. Portanto, a ordenada $y$ é positiva entre as raízes e negativa, fora. Ou seja,
\begin{eqnarray*}y=4-x^2>0 &\Leftrightarrow& -2<x<2; \\y=4-x^2<0 &\Leftrightarrow& x<-2 \text{ ou } x>2; \\y=4-x^2=0 &\Leftrightarrow& x=-2 \text{ ou } x=2;\end{eqnarray*}a parábola (iii), dada por $y=x^2-2x+2$, se enquadra no Caso (3a): não possui raízes reais e tem $a=1> 0$. Portanto, a ordenada $y$ é positiva em toda reta. Ou seja,
$$y=x^2-2x+2>0 \Leftrightarrow x \in \mathbb{R};$$a parábola (iv), dada por $y=-x^2+4x-4$ se enquadra no Caso (2b): possui apenas uma raiz real, a saber, $x_1=x_2=2$, e tem $a=-1< 0$: Portanto, a ordenada $y$ é negativa para todo $x$ diferente da raiz. Ou seja,
\begin{eqnarray*}y=-x^2+4x-4<0 &\Leftrightarrow& x \not=2\\y=-x^2+4x-4=0 &\Leftrightarrow& x=2.\end{eqnarray*}Se a expressão $y=ax^2+bx+c$, $x \in \mathbb{R}$, $a$, $b$, $c$ constantes reais e $a \not=0$ é tal que $\Delta \geq 0$, podemos fatorar esta expressão como o produto de duas expressões de primeiro grau. Vamos dividir em dois casos:
Neste caso, com algumas manipulações algébricas temos que,
\begin{eqnarray*}y & = & ax^2+bx+c=a\left(x + \frac{b}{a} + \frac{c}{a}\right)= a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a}\\& = & a\left(x -\left( \dfrac{-b-\sqrt{\Delta}}{2a}\right)\right)\left(x -\left( \dfrac{-b+\sqrt{\Delta}}{2a}\right)\right)\\& = &a\left(x -x_1\right)\left(x -x_2\right)\end{eqnarray*}Neste caso, temos que
\begin{eqnarray*}y & = & ax^2+bx+c=a\left(x + \frac{b}{a} + \frac{c}{a}\right)= a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a}\\& = & a\left(x + \frac{b}{2a}\right)^2 \\& = &a\left(x -x_1\right)^2\end{eqnarray*}Vamos fatorar as expressões dadas pelas parábolas de (i) a (iv):
a parábola (i), dada por $y=2x^2-8x+6$, possui duas raízes reais distintas, a saber, $x_1=3$ e $x_2=1$. Portanto,
\begin{eqnarray*}y=2x^2-8x+6 &=& a\left(x + \frac{b}{a} + \frac{c}{a}\right)= a\left(x -x_1\right)\left(x -x_2\right)\\&=& 2\left( x^2-4x+3\right)\\&=&2\left(x-1\right)\left(x-3\right);\end{eqnarray*}a parábola (ii), dada por $y=4-x^2$, possui duas raízes reais distintas, a saber, $x_1=2$ e $x_2=-2$. Portanto,
\begin{eqnarray*}y=4-x^2 &=& a\left(x + \frac{b}{a} + \frac{c}{a}\right)= a\left(x -x_1\right)\left(x -x_2\right)\\&=&-1\left(x^2-4\right)= -1\left(x-(-2)\right)\left(x-2\right)\\&=& -1\left(x+2\right)\left(x-2\right);\end{eqnarray*}a parábola (iii), dada por $y=x^2-2x+2$, não possui raízes reais. Portanto, não podemos fatorá-la (no ambiente dos números reais);
a parábola (iv), dada por $y=-x^2+4x-4$, possui apenas uma raiz real, a saber, $x_1=x_2=2$. Portanto,
\begin{eqnarray*}y=-x^2+4x-4 &=& a\left(x + \frac{b}{a} + \frac{c}{a}\right)= a\left(x -x_1\right)^2\\&=& -\left(x-2\right)^2.\end{eqnarray*}Para resolver a equação $ax^2+bx+c=0$, vamos, inicialmente, pensar em como resolvemos uma equação mais simples, que é uma equação do tipo $x^2+c=0$, isto é, a equação $ax^2+bx+c=0$, quando $a=1$ e $b=0$. Neste caso, temos que
que terá uma única solução real, a saber, $x=0$, se $c=0$; terá duas soluções reais, a saber, $x=\pm \sqrt{-c}$, se $c<0$ (nesse caso $-c>0$) e, finalmente, não terá solução real, se $c>0$, pois se $x$ é um elemento do conjunto dos números reais, $x^2$ que é este número elevado ao quadrado, ou ainda, este número vezes ele próprio, é sempre maior do que zero ou igual a zero, nunca podendo ser negativo. Nesse caso, você deve ter aprendido que a equação só admite soluções complexas, mas o conjunto dos números imaginários não terá parte nesta revisão, que tem por objetivo prepará-lo para o cálculo de funções reais de uma variável real.
A ideia por trás dos cálculos que se seguirão é transformar a equação $x^2 + \dfrac{b}{a}x + \dfrac{c}{a}$ numa equação parecida com a anterior. O que é este ``parecido''? É escrevê-la como um quadrado perfeito mais uma constante, isto é, na forma $(x+k_1)^2+k_2$, se for possível, é claro. Chamamos este processo de completar quadrados. (Ele será bastante utilizado no curso. Guarde-o com carinho!) Para tal, vamos primeiro recordar a fórmula do quadrado de uma soma: se $x$ e $k_1$ são dois números reais, então $(x+k_1)^2=x^2+2k_1x+k_1^2$ (este é o quadrado perfeito ao qual nos referimos).
Partindo da equação
\[ax^2 + bx + c = 0,\]como $a>0$, vamos reescrevê-la como abaixo, onde colocamos $a$ em evidência,
\[a\left(x^2 + \frac{b}{a}x + \frac{c}{a}\right) = 0.\]O próximo passo é tentar escrever o $x^2 + \dfrac{b}{a}x + \dfrac{c}{a}$ como um quadrado perfeito mais uma constante, isto é, na forma $(x+k_1)^2+k_2=x^2+2k_1x+k_1^2+k_2$ é comparar as duas expressões ($x^2 + \dfrac{b}{a}x + \dfrac{c}{a}$ e $x^2+2k_1x+k_1^2+k_2$). Observamos que o coeficiente do termo $x^2$ de ambas é 1 e que o coeficiente do termo $x$ em uma é $2k_1$ e na outra é $\dfrac{b}{a}$. Precisamos então fazê-los iguais, i.e.
\[2k_1 = \dfrac{b}{a}\therefore k_1 = \dfrac{b}{2a}.\]Com isso, o quadrado perfeito seria
\[\left(x+k_1\right)^2 = \left(x+\dfrac{b}{2a}\right)^2 = x^2 + 2\cdot \dfrac{b}{2a} x + \left(\dfrac{b}{2a}\right)^2 = x^2 + 2\cdot \dfrac{b}{2a} x + \dfrac{b^2}{4a^2}.\]Mas isso não é igual a $x^2 + \dfrac{b}{a}x + \dfrac{c}{a}$... e agora?
E agora, é a hora que entrará o papel da constante $k_2$. Vamos trabalhar na equação que temos, qual seja,
\[a\left(x^2 + \dfrac{b}{a}x + \dfrac{c}{a}\right) = a\left(x^2 + 2\cdot \dfrac{b}{2a}x + \dfrac{c}{a}\right) =0,\]somando e subtraindo, dentro do parênteses, um mesmo termo, no caso $ {\color{blue}\dfrac{b^2}{4a^2}}$, o que não altera a equação, mas fará nosso quadrado perfeito aparecer, conforme veremos a seguir.
Obtemos então
\[a\left(x^2 + 2\cdot \dfrac{b}{2a}x + \frac{c}{a} {\color{blue} + \frac{b^2}{4a^2} - \frac{b^2}{4a^2}}\right) = 0.\]Agrupando os termos dentro dos parênteses de forma mais visual, temos
\[a\left(\left(x^2 + 2\cdot \dfrac{b}{2a}x + \dfrac{b^2}{4a^2}\right) + \frac{c}{a} - \frac{b^2}{4a^2}\right) = 0,\]ou, equivalentemente,
\[a\left(\left(x + \dfrac{b}{2a}\right)^2 + \frac{c}{a} -\dfrac{b^2}{4a^2}\right) = 0.\]Multiplicando agora o $a$ pelos termos de dentro dos parênteses, obtemos
\[a\left(x + \frac{b}{2a}\right)^2 + a\cdot\frac{c}{a} - a\cdot\frac{b^2}{4a^2} = 0,\]ou ainda
\[a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a} = 0.\]Com isso,
\[a\left(x + \frac{b}{2a}\right)^2 = \frac{b^2}{4a} - c,\]que equivale a (colocando o lado direito sobre o mesmo denominador $4a$)
\[a\left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a}.\]Lembrando que $\Delta = b^2-4ac$, temos
\[a\left(x + \frac{b}{2a}\right)^2 = \frac{\Delta}{4a},\]que, dividindo por $a$, equivale a
\[\left(x + \frac{b}{2a}\right)^2 = \frac{\Delta}{4a^2}.\]Como $4a^2$ é sempre positivo, o sinal de $\Delta$ é que determinará o sinal da fração $\dfrac{\Delta}{4a^2}$. Neste caso, temos que a equação $ax^2+bx+c=0$:
possui duas soluções reais distintas se, e somente se, $\Delta > 0$, sendo estas
\[x_1 = -\frac{b}{2a} +\dfrac{\sqrt{\Delta}}{2a}= \frac{-b+\sqrt{\Delta}}{2a} \text{ e } x_2 = -\frac{b}{2a} -\dfrac{\sqrt{\Delta}}{2a}= \frac{-b-\sqrt{\Delta}}{2a},\]ou, escrito de forma condensada
\[x = -\frac{b}{2a} \pm\dfrac{\sqrt{\Delta}}{2a}= \frac{-b\pm\sqrt{\Delta}}{2a}.\]possui duas soluções reais iguais se, e somente se, $\Delta = 0$, sendo esta
\[x = \frac{-b}{2a}.\]não possui soluções reais se, e somente se, $\Delta < 0$,
Eis a razão de ser da Fórmula de Bhaskara!
P.S. O caso $a<0$ é resolvido de forma análoga, chegando-se na mesma fórmula.