
Muitos resultados e aplicações importantes que estudaremos daqui para frente dependem dos teoremas dessa seção. Esses teoremas são estruturais dentro do Cálculo, são eles o Teorema de Rolle e o Teorema do Valor Médio. Utilizando-os, poderemos extrair informações a respeito de uma função através de propriedades de sua derivada.
(Teorema de Rolle) Seja f uma função tal que:
$f$ é contínua no intervalo fechado $[a,b]$
$f$ é derivável no intervalo aberto $(a,b)$;
$f(a)=f(b)$.
Então, existe pelo menos um ponto $c \in (a,b)$, tal que $f'(c)=0$.

A reta tangente $r_t$ é paralela ao eixo $x$, $f'(c)=0$.
De um ponto de vista geométrico, o Teorema de Rolle garante que, nas hipóteses do Teorema, existe pelo menos um ponto $c$ no intervalo $(a,b)$, onde a reta tangente é horizontal. Do ponto de vista físico, se $s=f(t)$ for a função posição de um objeto em movimento, o Teorema de Rolle nos diz que se o objeto ocupar duas vezes a mesma posição ($f(a)=f(b)$) em instantes $a$ e $b$ diferentes, então em algum momento $t=c$, durante esse intervalo de tempo, sua velocidade se anulou, ou seja $v(c)=f'(c)=0$.
O Teorema do Valor Médio (também conhecido como Teorema de Lagrange), é uma engenhosa adaptação do Teorema de Rolle, que permite eliminar a condição $f(a)=f(b)$.
(Teorema do Valor Médio) Seja f uma função tal que:
$f$ é contínua no intervalo fechado $[a,b]$;
$f$ é derivável no intervalo aberto $(a,b)$;
Então, existe pelo menos um ponto $c \in (a,b)$, tal que $f'(c)= \frac{f(b)-f(a)}{b-a}.$
Sabemos que a razão
\[\frac{f(b)-f(a)}{b-a} = \frac{\Delta f}{\Delta x}\]é a variação média da função entre $x=a$ e $x=b$. O Teorema do Valor Médio (TVM) garante que, se a função cumpre as condições da hipótese, então haverá pelo menos um ponto $x=c$ onde a derivada $f'(c)$ é igual à variação média da $f$ no intervalo $[a,b]$.
De um ponto de vista geométrico, o Teorema do Valor Médio (TVM) garante que existe uma reta tangente ao gráfico da $f$ num ponto intermediário $c$, com $a<c<b$, que é paralela à corda que passa pelos pontos $(a, f(a))$ e $(b, f(b))$.
Quando a referida corda é horizontal, i.e. quando $f(a)=f(b)$, a tangente é horizontal, o que mostra que o Teorema de Rolle é um caso especial do Teorema do Valor Médio.
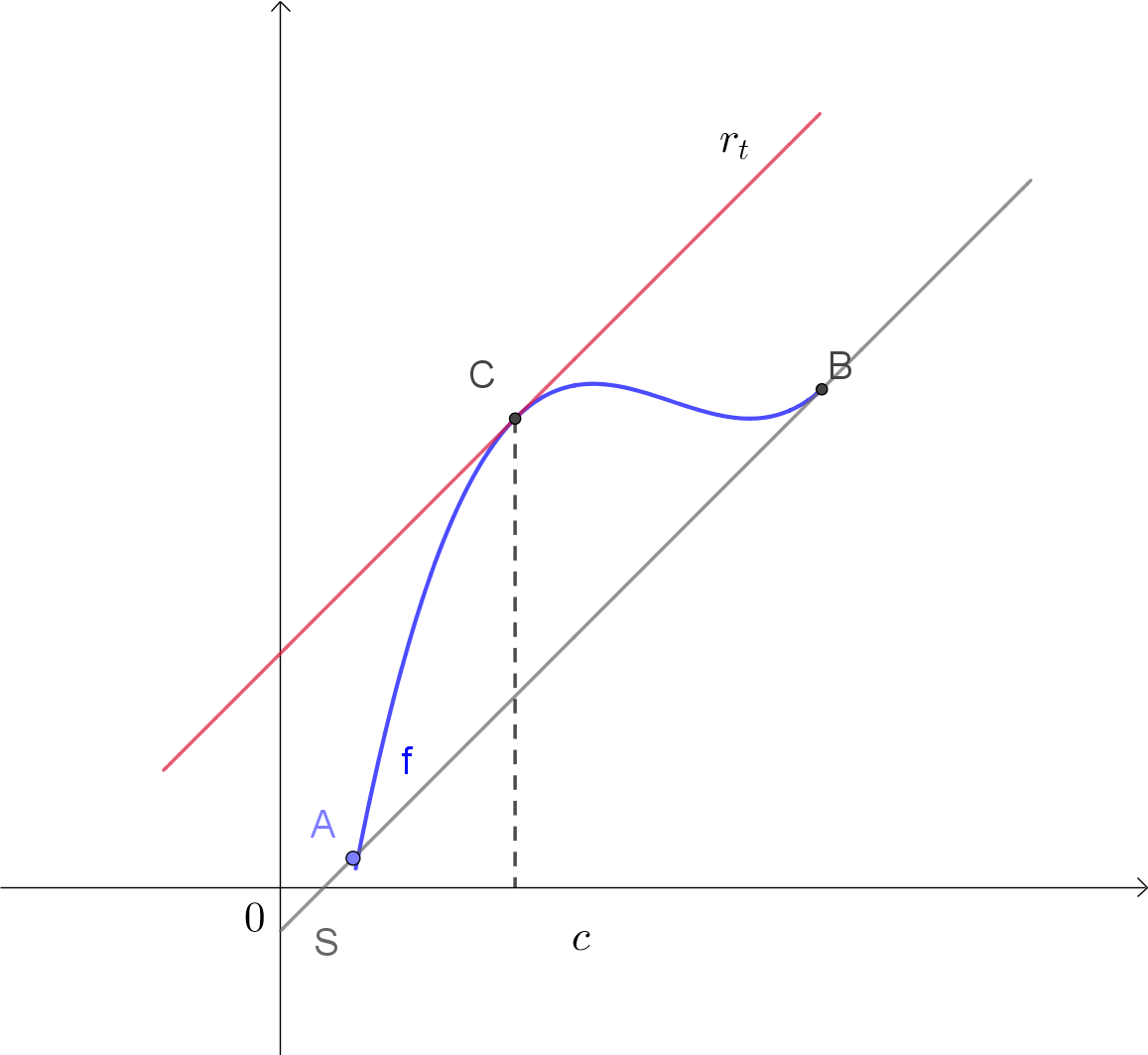
A reta tangente $r_t$ é paralela à corda $S$, $f'(c)=\frac{f(b)-f(a)}{b-a}$, onde $A=(a,f(a))$ e $B=(b,f(b))$.
Seja $f(x)=x^2-x$, para $x\in[0,4]$. Vamos ilustrar o TVM através deste exemplo. Como a função $f$ é polinomial, será derivável em todo intervalo $(0,4)$ e também contínua em $[0,4]$. Aplicando o TVM, temos que existe $c\in(0,4)$, tal que $f'(c)=\frac{f(4)-f(0)}{4-0}=12/4=3.$ Mas, nesse caso $f'(x)=2x-1$, portanto conseguimos determinar a abscissa $x=c$, ou seja, $2c-1=3 \Rightarrow c=2$. Veja a figura a seguir.
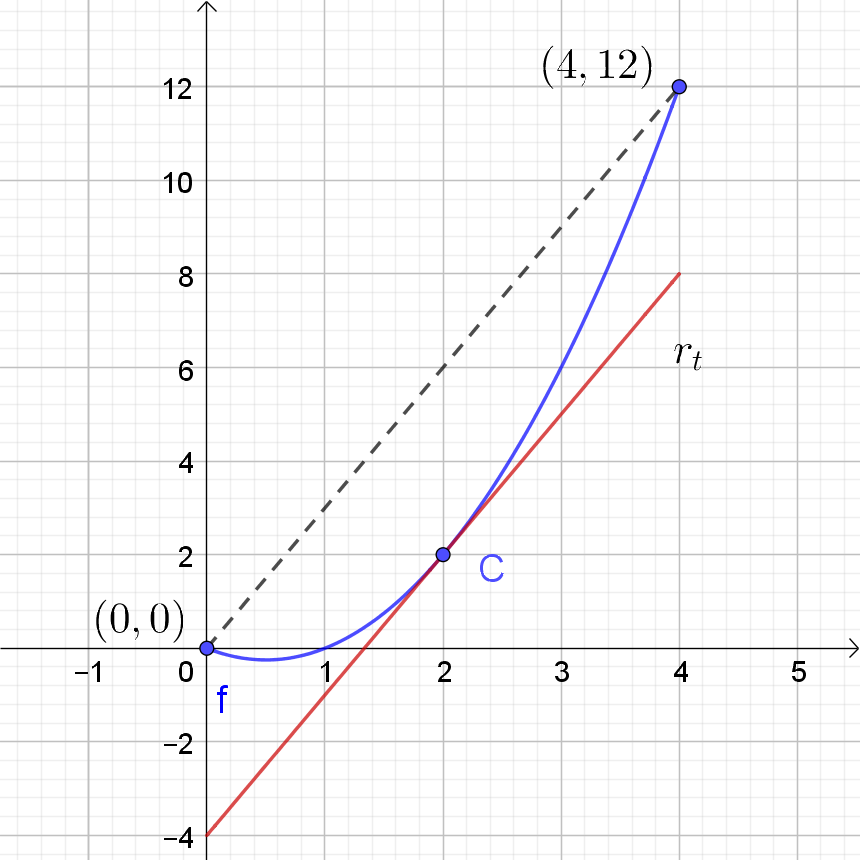
A reta tangente $r_t$ é paralela à corda que passa por $(0,0)$ e $(4,12)$.
Quando um objeto se move em linha reta com uma função posição $s(t)$, $t\in[a,b]$, o TVM nos diz que em algum instante nesse intervalo, sua velocidade instantânea foi igual à sua velocidade média. De fato, pelo TVM, existe $c\in(a,b)$, tal que $ s'(c)= \dfrac{s(b)-s(a)}{b-a} $, mas $s'(c)$ é a velocidade no instante $t=c$ e o lado direito da igualdade, que pode ser escrito como $\dfrac{\Delta s}{\Delta t}$ é a velocidade média do objeto durante o intervalo de tempo $[a,b]$.
Supondo que para uma função $f:\mathbb{R}\longrightarrow \mathbb{R}$ derivável, se tenha $f(0)=1$ e $f'(x)\leq 7/2, \forall x \in \mathbb{R}$, qual o maior valor possível para $f(2)$?
Aplicando o TVM a $f$ em $[0,2]$, temos que existe $c\in(0,2)$, tal que
$$\dfrac{f(2)-f(0)}{2-0}=f'(c) \Rightarrow f(2)-1=2f'(c)\Rightarrow f(2) \leq1+ 2 \, \frac{7}{2}=8.$$ Assim, o maior valor possível para $f(2)$ é $8$.
O Teorema do Valor Médio nos permite identificar intervalos onde a função $f$ é monótona, ou seja, onde é crescente ou decrescente, pela determinação do sinal de sua derivada $f'$, tal como descreveremos a seguir. Mais à frente, veremos que este estudo será útil para classificar se um ponto onde a derivada de $f$ se anula é um ponto de máximo ou de mínimo, ou ainda se não é nenhum dos dois.
Dizemos que uma função é estritamente crescente em seu domínio $I$, se dados quaisquer $x<t$ em $I$, tivermos $f(x)<f(t)$. Analogamente, será estritamente decrescente em seu domínio $I$, se dados quaisquer $x<t$ em $I$, tivermos $f(x)>f(t)$.Se $f$ é contínua no intervalo $I=[a,b]$ e derivável em $(a,b)$ então:
$f'(x) =0, \; \forall x \in (a,b) \; \Rightarrow f$ é constante no intervalo $[a,b]$;
$f'(x) >0, \; \forall x \in (a,b) \; \Rightarrow f$ é estritamente crescente no intervalo $[a,b]$;
$f'(x) <0, \; \forall x \in (a,b) \; \Rightarrow f$ é estritamente decrescente em $[a,b]$;
Observe que o Teorema 3 anterior nos dá uma recíproca para o fato de uma função constante ter derivada zero. Porém, ter derivada zero implica em ser uma função constante só quando o domínio é um intervalo. Por exemplo, a função $y=\frac{|x|}{x}$, $\forall x\neq 0$, tem derivada nula, mas não é constante. Note que seu domínio não é um intervalo, mas uma união de dois intervalos disjuntos.
Outra consequência importante é dada na proposição seguinte, que nos diz que se duas funções possuem derivadas iguais em todo o ponto de um intervalo $I$, então elas diferem por uma constante, ou seja, uma é translação vertical da outra.
Se $f'(x)=g'(x), \forall x\in I$, onde I é um intervalo, então existe uma constante $k$, tal que $f(x)=g(x)+k, \forall x \in I$ .
Por exemplo, da proposição anterior, segue que as únicas funções que possuem derivada igual a $e^x$ são do tipo $e^x+k$, pois sabemos que a derivada de $e^x$ é ela própria em $\mathbb{R}$ e qualquer outra que tenha $e^x$ como derivada será uma translação vertical da mesma. Chamamos uma função $F(x)$, tal que $F'(x)=f(x)$, $\forall x \in I$ de uma primitiva da $f$ e a família de todas as primitivas de uma $f$ é dita a integral indefinida da $f$ e é denotada por
$$\int f(x)dx=F(x)+k, x\in I.$$
Temos $\int e^x dx=e^x+k$ $\int \cos(x) dx=\mathrm{sen}(x)+k$, $\int \mathrm{sen}(x) dx=-\cos(x)+k$, $\int \sec^2(x) dx=\mathrm{tg}(x)+k$, $\int x^2 dx=\frac{x^3}{3} +k$ e assim por diante. Na disciplina Cálculo IIA esse assunto será central!
Nas semanas anteriores, quando introduzimos o conceito de limite, já encontramos formas indeterminadas do tipo, por exemplo, $[\frac{0}{0}]$. Para funções racionais resolvemos o problema "eliminando" fatores comuns, como por exemplo nesse caso:
$$\lim_{x \to 1} \frac{x^2-x}{x^2-1}= \lim_{x \to 1} \frac{x(x-1)}{(x+1)(x-1)} = \lim_{x \to 1} \frac{x}{x+1} = \frac{1}{2},$$enquanto usamos um argumento geométrico para o limite trigonométrico fundamental
$$\lim_{x\to 0} \frac{\mathrm{sen} \, x}{x} =1.$$Mas essas técnicas não funcionam em generalidade. Agora que temos a derivação na nossa aljava, podemos introduzir um método sistemático, a regra de L'Hospital, para o cálculo de limites em formas indeterminadas.
Como não faremos uma demonstração do resultado, daremos um argumento usando polinômio de Taylor, válido sob certas hipóteses, para mostrar que o resultado é de se esperar. A regra de L'Hospital nos diz que quando há uma indeterminação, é possível calcular o limite de um quociente de funções olhando para o limite do quociente de suas derivadas no mesmo ponto. Assim, tomemos $a\in I$ e sejam $f$ e $g$ funções de classe $C^2$ em I, tais que $f(a)=g(a)=0$ e $g'(a)\neq 0$. Usando os polinômios de Taylor dessas funções de ordem 1 em torno de $x=a$, obtemos que
pois do Teorema de Taylor (visto no texto sobre Polinômio de Taylor), $\frac{\overline{E}rro(x)}{(x-a)}\to 0$ e $\frac{ Erro(x)}{(x-a)}\to 0$, quando $x\to a$. E, além disso $\lim_{x\to a} \frac{f'(x)}{g'(x)}=\dfrac{f'(a)}{g'(a)}$, já que supomos $g'(a)\neq 0$, $f'$ e $g'$ contínuas em $a$. Portanto, chegamos ao resultado
$$\lim_{x\to a} \dfrac{f(x)}{g(x)} =\lim_{x\to a} \dfrac{f'(x)}{g'(x)}.$$Acima, colocamos várias hipóteses sobre as funções envolvidas, porém da regra de L'Hospital vale num contexto mais geral, como veremos no resultado a seguir.
(Regra de L'Hospital) Seja $a\in I$ um intervalo aberto e sejam $f$ e $g$ funções deriváveis em I (exceto possivelmente em $a$), tal que $g'(x) \neq 0$ para todo $x \in I \setminus \{a\} $.
Suponhamos também que
$$\lim_{x \to a} f(x) = \lim_{x \to a} g(x) = 0 $$ou
$$\lim_{x \to a} f(x) =\pm \infty \ e \ \lim_{x \to a} g(x) = \pm \infty.$$Se existe ou é infinito o limite $\lim_{x\to a} \frac{f'(x)}{g'(x)}$, então
$$\lim_{x\to a} \frac{f(x)}{g(x)} = \lim_{x\to a} \frac{f'(x)}{g'(x)}$$A Regra de L'Hospital é válida também para os limites laterais ou para limites em $\infty$ e em $- \infty$, isto é "$x \to a$" pode ser substituído por "$x \to a^+$", "$x \to a^-$", "$x \to \infty$" e "$x \to - \infty$".
Consideramos a função $f(x)= \dfrac{\ln x}{x-1}$ no seu domínio natural $D=\{x \in \mathbb{R} \mid x>0, x\neq 1\}$, e queremos calcular
$$\lim_{x \to 1} \frac{\ln x}{x-1}.$$Vemos que temos uma indeterminação do tipo $[0/0]$ e nesse caso, podemos aplicar a regra de L´Hospital diretamente. Logo,
\[\lim_{x \to 1} \frac{\ln x}{x-1}= \lim_{x \to 1}\dfrac{\frac{1}{x}}{1}= \lim_{x \to 1}\frac{1}{x}=1.\]Agora, queremos calcular $\lim_{x \to \pi^+} \dfrac{\mathrm{sen}(x)}{\cos(x)+1}$, que possui uma indeterminação do tipo $[0/0]$ e nesse caso, também podemos aplicar L´Hospital diretamente.
Logo,
\[\lim_{x \to \pi^+} \dfrac{\mathrm{sen}(x)}{\cos(x)+1}=\lim_{x \to \pi^+} \dfrac{\cos(x)}{-\mathrm{sen}(x)}=-\infty\]
O próximo exemplo ilustra o fato de que às vezes somos levados a aplicar a Regra de L'Hospital (L'H) mais de uma vez. Isso acontece quando aplicamos e caímos em outra indeterminação.
No $\lim_{x \to 0}\dfrac{\mathrm{tg}(x)-x}{x^3}$ também temos uma indeterminação do tipo $[0/0]$, então aplicando L'H temos,
$$\lim_{x \to 0}\dfrac{\mathrm{tg}(x)-x}{x^3}=\lim_{x \to 0}\dfrac{\sec^2(x)-1}{3x^2},$$que continua indeterminado. Aplicando L'H novamente, obtemos,
$$\lim_{x \to 0}\dfrac{\sec^2(x)-1}{3x^2}=\lim_{x \to 0}\dfrac{2\sec^2(x)\mathrm{tg}(x)}{6x}$$e ainda está indeterminado! Aplicamos L´H pela última vez e obtemos
$$\lim_{x \to 0}\dfrac{2\sec^2(x)\mathrm{tg}(x)}{6x}=\lim_{x \to 0}\dfrac{4\sec^2(x)\mathrm{tg}^2 (x)+2\sec^4(x)}{6}=1/3 \ \ (*)$$Assim, $ \lim_{x \to 0}\dfrac{\mathrm{tg}(x)-x}{x^3}=1/3.$
Vale a pena observar que em $(*)$ poderíamos ter usado o limite trigonométrico fundamental no lugar de L'H pela 3ª vez, pois $ \lim_{x \to 0}\dfrac{2\sec^2(x)\mathrm{tg}(x)}{6x}=\lim_{x \to 0}\dfrac{2\mathrm{sen}(x) }{6x\cos^3(x)}=\lim_{x \to 0}\dfrac{\mathrm{sen}(x) }{x}\dfrac{1}{3\cos^3(x)}=1/3$.
Nesse exemplo $\lim_{x \to +\infty} \dfrac{\ln x}{x}$, temos uma indeterminação do tipo $[\infty/\infty]$. Aplique L'H.
Esse exemplo nos mostra que a exponencial cresce mais rápido do que qualquer polinômio. Observe:
$\lim_{x \to +\infty} \dfrac{e^x}{x}=\lim_{x \to +\infty} \dfrac{e^x}{1}=+\infty$, pois temos uma indeterminação do tipo $[\infty/\infty]$ e podemos aplicar L'H.
$\lim_{x \to +\infty} \dfrac{e^x}{x^2}=\lim_{x \to +\infty} \dfrac{e^x}{2x}=\lim_{x \to +\infty} \dfrac{e^x}{2}=+\infty$, pois aplicamos L'H duas vezes.
Se $n\geq 3$ for natural, então $\lim_{x \to +\infty} \dfrac{e^x}{x^n}=\lim_{x \to +\infty} \dfrac{e^x}{nx^{n-1}}=...=\lim_{x \to +\infty} \dfrac{e^x}{n!}=+\infty$, pois aplicamos L'H $n$ vezes.
Se $p(x)$ é um polinômio de grau $n$ podemos aplicar L'H $n$ vezes para obter $\lim_{x \to +\infty} \dfrac{e^x}{p(x)}=+\infty$, se o coeficiente de $x^n$ for positivo, ou $\lim_{x \to +\infty} \dfrac{e^x}{p(x)}=-\infty$ se o coeficiente de $x^n$ for negativo.
A partir do exemplo seguinte vamos ver como podemos utilizar a regra de L'Hospital nos outros tipos de indeterminações. Na verdade, teremos sempre que reescrever a função de tal forma que cheguemos a uma indeterminação do tipo $[0/0]$ ou $[\infty/\infty]$.
Vejamos o caso de uma indeterminação tipo $[0\cdot\infty]$ através do exemplo:
\[\lim_{x \to 0^+}x\ \ln(x).\]Não podemos aplicar diretamente L'H, pois não temos uma indeterminação [0/0] ou $[\infty/\infty]$. A ideia será transformar o produto em quociente, sem modificar a função original, para que tenhamos uma indeterminação do tipo $[0/0]$ ou $[\infty/\infty]$. Observe:
\[\lim_{x \to 0^+}x\ \ln(x)=\lim_{x \to 0^+}\dfrac{\ln(x)}{\frac{1}{x}}\underset{ind. [\infty/\infty]}{=}\lim_{x \to 0^+}\dfrac{\frac{1}{x}}{-\frac{1}{x^2}}=\lim_{x \to 0^+}-x=0.\]Nesse caso, foi mais simples inverter o $x$ do que inverter o $\ln(x)$.
Vejamos outro caso de uma indeterminação tipo $[0\cdot\infty]$:
$$\lim_{x \to +\infty} e^{-x}ln(x)=\lim_{x \to +\infty}\dfrac{\ln(x)}{e^x}\underset{ind. [\infty/\infty]}{=}\lim_{x \to +\infty}\dfrac{\frac{1}{x}}{e^x}=\lim_{x \to +\infty}\dfrac{1}{xe^x}=0.$$Nesse exemplo temos uma indeterminação do tipo $[\infty-\infty]$, que resolveremos convertendo em uma indeterminação do tipo [0/0]:
$$\lim_{x \to \pi/2}\sec(x)-\mathrm{tg}(x)=\lim_{x \to \pi/2} \dfrac{1}{\cos(x)}-\dfrac{\mathrm{sen}(x)}{\cos(x)}=\lim_{x \to \pi/2} \dfrac{1-\mathrm{sen}(x)}{\cos(x)}\underset{ind.[0/0]}{=} \lim_{x \to \pi/2} \dfrac{-\cos(x)}{-\mathrm{sen}(x)}=0.$$Outro exemplo interessante com indeterminação tipo $[\infty - \infty]$, que será convertido em uma indeterminação do tipo $[\infty/\infty]$:
$$\lim_{x \to +\infty}x-\ln(x)=\lim_{x \to +\infty}x \left(1-\dfrac{\ln(x)}{x}\right).$$Vimos no exemplo 7 que $\lim_{x \to +\infty}\dfrac{\ln(x)}{x}=0$, logo
$$\lim_{x \to +\infty}x \left(1-\dfrac{\ln(x)}{x}\right)=+\infty.$$
Lembramos que definimos uma função elevada a outra função da seguinte forma:
desde que $f$ e $g$ estejam definidas em $I$ e $f(x)>0, \forall x \in I$. Assim, sempre que houver um limite com indeterminação $[0\cdot\infty]$ no expoente $g(x)\ln(f(x))$, teremos indeterminação correspondente em $f^g$. As possíveis indeterminações são: $[1^\infty],[0^0]$ e $[\infty^0]$.
Um exemplo com indeterminação tipo $[1^\infty]$:
$$\lim_{x \to 0}(1+\pi x)^{1/x}=\lim_{x \to 0}e^{\frac{1}{x}\ln(1+\pi x)} \ (*)$$Separamos o expoente em $(*)$ e calculamos seu limite por L'H:
$$\lim_{x \to 0}{\frac{1}{x}\ln(1+\pi x)}=\lim_{x \to 0}{\dfrac{\ln(1+\pi x)}{x}}\underset{ind.[0/0]}{=}\lim_{x \to 0}{\dfrac{ \pi}{1+ \pi x}}= \pi.$$Voltando a $(*)$, como a exponencial é contínua, temos que
$$\lim_{x \to 0}(1+\pi x)^{1/x}=\lim_{x \to 0}e^{\frac{1}{x}\ln(1+\pi x)}=e^{\lim_{x \to 0}\frac{1}{x}\ln(1+\pi x)}=e^{\pi}.$$Um exemplo com indeterminação tipo $[0^0]$:
$$\lim_{x \to 0^+}x^x=\lim_{x \to 0^+}e^{x\ln(x)}= e^{\lim_{x\to 0^+}x\ln(x)}=e^0=1, $$pois, o limite do expoente já foi calculado no exemplo 9.
Um exemplo com indeterminação tipo $[\infty^0]$:
$$\lim_{x \to +\infty}x^{1/x^2}=\lim_{x \to +\infty}e^{\frac{\ln(x)}{x^2}} \ (*)$$Separando o expoente, que possui indeterminação tipo $[\infty/\infty]$, pela regra de L'H, segue que
$$\lim_{x \to +\infty} \dfrac{\ln(x)}{x^2}=\lim_{x \to +\infty}\dfrac{\frac{1}{x}}{2x}=\lim_{x \to +\infty}\dfrac{1}{2x^2}=0$$Retornando a $(*)$, obtemos que
$$\lim_{x \to +\infty}x^{1/x^2}=\lim_{x \to +\infty}e^{\frac{\ln(x)}{x^2}}=e^0=1$$
Calcule os limites abaixo, se possível. Antes de fazer contas sem pensar, devemos sempre investigar o que está acontecendo com as funções envolvidas no limite no ponto dado, pois nem sempre é necessário ou possível usar L'Hospital.
$ \lim_{x \to -\infty} e^{-x^2}x$
$ \lim_{x \to -\infty} \dfrac{e^x}{x}$
$ \lim_{x \to 0^+}\left(\dfrac{1}{x}-\mathrm{cosec}(x)\right)$
$\ \lim_{x \to +\infty}\dfrac{x}{\sqrt{x^2+1}}$
$ \lim_{x \to +\infty}\ln(x)-\ln(2x+1)$
$ \lim_{x \to 0^+}\left(\mathrm{arcsen}(x)\right)^{1/x}$
Há indeterminação do tipo $[0\cdot\infty]$ e reescrevendo, temos
$$ \lim_{x \to -\infty} e^{-x^2}x \underset{ind.[\infty/\infty]}{=}\lim_{x \to -\infty} \dfrac{x}{e^{x^2}}\underset{L'H}{=}\lim_{x \to -\infty} \dfrac{1}{2xe^{x^2}}=0$$Nesse caso, não há indeterminação, já que $e^x\to 0$ e $1/x\to 0$, se $x\to -\infty$, portanto
$$ \lim_{x \to -\infty}\dfrac{e^x}{x}=\lim_{x \to -\infty}\dfrac{1}{x}e^x= 0.$$
Quando não há indeterminação, não podemos usar L'Hospital!!!
Vamos reescrever a cossecante e tirar o MMC:
$$ \lim_{x \to 0^+}\left(\dfrac{1}{x}-\mathrm{cosec}(x)\right)=\lim_{x \to 0^+}\dfrac{\mathrm{sen}(x)-x}{x\,\mathrm{sen}(x)}\underset{ind.[0/0],L'H}{=}$$$$ =\lim_{x \to 0^+}\dfrac{\cos(x)-1}{\mathrm{sen}(x)+x\cos(x)}\underset{ind.[0/0],L'H}{=}\lim_{x \to 0^+}\dfrac{-\mathrm{sen}(x)}{2\cos(x)-x\,\mathrm{sen}(x)}=0.$$
Nossa primeira tentativa será usando L´H, pois há uma indeterminação do tipo $[\infty/\infty]$, assim
$$\lim_{x \to +\infty}\dfrac{x}{\sqrt{x^2+1}}\underset{L'H}{=}\lim_{x \to +\infty}\dfrac{1}{\frac{x}{\sqrt{x^2+1}}}=\lim_{x \to +\infty}\dfrac{\sqrt{x^2+1}}{x}$$e temos nova indeterminação do tipo $[\infty/\infty]$. Aplicando a regra de L'H novamente, retornamos à função inicial, ou seja,
$$\lim_{x \to +\infty}\dfrac{\sqrt{x^2+1}}{x}\underset{L'H}{=}\lim_{x \to +\infty}\dfrac{x}{\sqrt{x^2+1}}.$$Não adianta continuar! A Regra de L'Hospital não vai nos ajudar nesse caso! Portanto, vamos lembrar das primeiras aulas sobre limite...
Temos indeterminação do tipo $[\infty-\infty]$. Nesse caso, utilizaremos propriedade do logaritmo para escrever:
$$\lim_{x \to +\infty}\ln(x)-\ln(2x+1)=\lim_{x \to +\infty}\ln\left(\frac{x}{2x+1}\right).$$Observe que $\lim_{x \to +\infty}\frac{x}{2x+1}=1/2$(aqui pode usar L´H ou dividir numerador e denominador por $x$). Logo,
$$\lim_{x \to +\infty}\ln\left(\frac{x}{2x+1}\right)=\lim_{t \to 1/2}\ln(t)=\ln(1/2)=-\ln(2),$$pois $\ln$ é contínua em $(0,+\infty)$.
Observe que
$$\left(\mathrm{arcsen}(x)\right)^{1/x}=e^{\frac{1}{x}\ln(\mathrm{arcsen}(x))}$$e que $1/x \to +\infty$ e $\ln(\mathrm{arcsen}(x)) \to -\infty$, quando $x\to 0^+$, portanto NÃO há indeterminação, mas o produto das duas tende a $-\infty$, donde se conclui que $\lim_{x \to 0^+}\left(\mathrm{arcsen}(x)\right)^{1/x}=\lim_{x \to 0^+}e^{\frac{1}{x}\ln(\mathrm{arcsen}(x))}=0.$
Se o limite $ \lim_{x\to a} \frac{f'(x)}{g'(x)} $ não existe, nesse caso não podemos concluir nada sobre a existência ou não do limite $\lim_{x\to a} \frac{f(x)}{g(x)} $ e sobre seu eventual valor.
Considere $f(x)= x^2 \mathrm{sen}(1/x)$ e $g(x)=x$. Observe que $ \lim_{x\to 0} \frac{f(x)}{g(x)}= \lim_{x\to 0} \frac{ x^2 \mathrm{sen}(1/x)}{x}= \lim_{x\to 0}x\,\mathrm{sen}(1/x)=0$, pelo Teorema do Anulamento. No entanto, se quiséssemos aplicar a regra de L'Hospital, pois há uma indeterminação do tipo $[0/0]$, teríamos que calcular
mas esse limite NÃO EXISTE.