
Nos exemplos a seguir vamos esboçar os gráficos das funções no maior domínio que podemos considerar para as expressões dadas. Assim, nossa primeira tarefa será determinar cada domínio. A seguir, podemos localizar as interseções com os eixos coordenados (caso existam), verificar se a função é par ou ímpar (se for, podemos traçar a parte do gráfico para variável positiva e fazer uma reflexão), calcular o(s) limite(s) no infinito e ver se existe alguma assíntota horizontal, ver se existe algum "candidato" a assíntota vertical e fazer os limites laterais nesses pontos ( os candidatos são os pontos onde há possibilidade de algum limite lateral dar infinito, tipo ponto fora do domínio, mas onde se pode calcular limite), olhar o sinal da primeira derivada para saber o crescimento e extremos locais da função, estudar o sinal da segunda derivada para saber sobre a concavidade do gráfico e os pontos de inflexão. Se precisar, calculamos a função em alguns outros pontos só para "guiar" o gráfico. Depois de pronto, podemos ver se há extremos absolutos e ainda dizer qual é o conjunto imagem.
$f(x)=2x^3-3x^2-12x$.
Domínio: $\mathbb{R}$
Interseções com os eixos:
Eixo $x$:
$f(x)=2x^3-3x^2-12x=0 \Leftrightarrow x=0 \ \ ou \ \ 2x^2-3x-12=0 \Leftrightarrow x=0 \ \ ou \ \ x=\dfrac{3\pm \sqrt{105}}{4}$.
Pontos de interseção com o eixo $x$: $(0,0)$, $\left(\dfrac{3- \sqrt{105}}{4},0\right)$ e $\left(\dfrac{3+\sqrt{105}}{4},0\right)$.
Eixo $y$: $f(0)=0$, temos $(0,0)$.
A $f$ não é par e nem ímpar, por exemplo $f(-1)=7 \neq \pm f(1)=-13$.
Não há assíntotas horizontais:
$$\displaystyle \lim_{x\to +\infty}2x^3-3x^2-12x=\lim_{x\to +\infty}x^3(2-3/x-12/x^2)=+\infty$$ $$\displaystyle \lim_{x\to -\infty}2x^3-3x^2-12x=\lim_{x\to -\infty}x^3(2-3/x-12/x^2)=-\infty$$Não há assíntotas verticais, pois a $f$ é contínua em $\mathbb{R}$.
Intervalos de crescimento/decrescimento e extremos locais:
Precisamos olhar o sinal da derivada de 1ª ordem da $f$, mas fizemos esse estudo anteriormente, então
Assim, a $f$ é estritamente crescente em $(-\infty,-1)$ e em $(2,+\infty)$ e estritamente decrescente em $(-1,2)$, sendo $x=-1$ ponto de máximo local e $x=2$ de mínimo local da $f$. No gráfico temos os pontos $(-1,7) \, e ,\ (2,-20)$.
Concavidade e inflexão:
Vimos no Exemplo 1 da página anterior que
$$f''(x)>0 \Leftrightarrow x\in (1/2,+\infty);\ \ f''(x)<0 \Leftrightarrow x\in (-\infty,1/2).$$E, portanto, a $f$ tem concavidade para cima em $(1/2,+\infty)$ e para baixo em $(-\infty,1/2)$, sendo, , $x=1/2$ o único ponto de inflexão. No gráfico, o ponto de inflexão é dado por $(1/2,-13/2)$.
Agora, reunimos as informações obtidas e colocamos no gráfico. Começamos com os pontos obtidos nos ítens acima: interseções com os eixos, extremos locais e inflexão.
Note que $\dfrac{3- \sqrt{105}}{4}\approx -1,8$ e $\dfrac{3+\sqrt{105}}{4}\approx 3,3$.
Esboço do gráfico:
Observe que não há extremos absolutos e o conjunto imagem é $\mathbb{R}$.
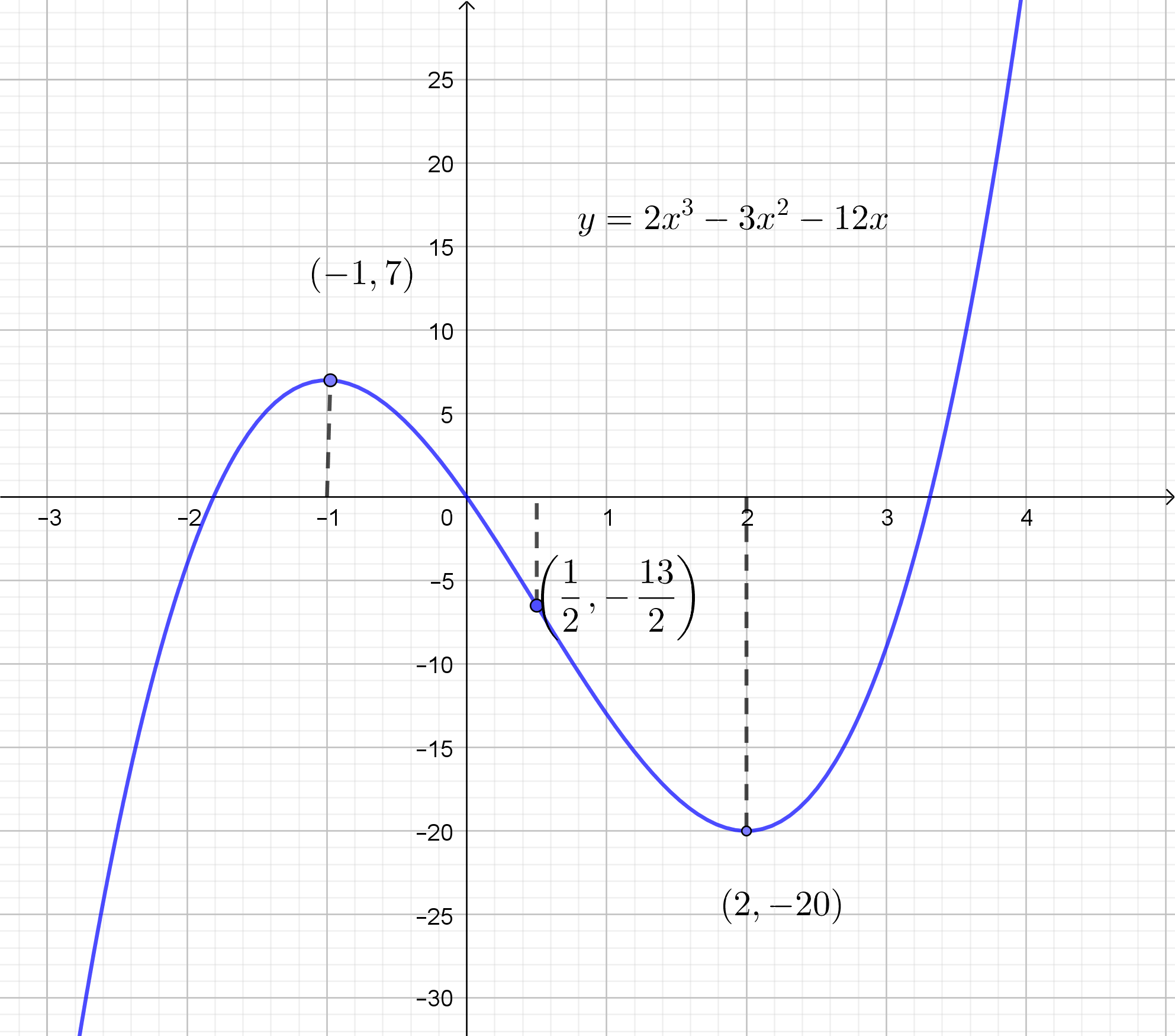
Esboço do gráfico de $f(x)=2x^3-3x^2-12x$.
$f(x)=\dfrac{x^2-1}{x^2-4}$.
Domínio: $\mathbb{R}\setminus\{ \pm 2 \}$
Interseções com os eixos:
Eixo $x$:
$f(x)=\dfrac{x^2-1}{x^2-4}=0 \Leftrightarrow x=\pm 1$.
Pontos de interseção com o eixo $x$: $(1,0)$ e $(-1,0)$.
Eixo $y$: $f(0)=1/4$, temos $(0,1/4)$.
A $f$ é par, pois $f(-x)=\dfrac{(-x)^2-1}{(-x)^2-4}=\dfrac{x^2-1}{x^2-4}=f(x), \forall x \neq \pm2$. Portanto, podemos fazer os demais cálculos para $\boldsymbol{x\geq 0, x \neq2}$ e depois completar o gráfico fazendo simetria em relação ao eixo $\boldsymbol{y}$.
Assíntota horizontal:
$$ \displaystyle \lim_{x\to +\infty}\dfrac{x^2-1}{x^2-4}=\lim_{x\to +\infty}\dfrac{1-\frac{1}{x^2}}{1-\frac{4}{x^2}}=1$$Logo, a reta $y=1$ é uma assíntota horizontal do gráfico da $f$.
Assíntotas verticais: vamos procurar em $x=2$, pois é o único ponto para $x\geq 0$, fora do domínio onde podemos calcular limite e tem chance de ser infinito. De fato,
$$\displaystyle \lim_{x\to 2^+}\dfrac{x^2-1}{x^2-4}=+\infty$$ $$\displaystyle \lim_{x\to 2^-}\dfrac{x^2-1}{x^2-4}=-\infty$$Com os cálculos acima, sabemos o comportamento do gráfico quando nos aproximamos de $2$ tanto pela direita , como pela esquerda e ainda temos que a reta $x=2$ é uma assíntota vertical do gráfico.
Intervalos de crescimento/decrescimento e extremos locais:
Precisamos olhar o sinal da derivada de 1ª ordem da $f$:
Para $x\geq 0, x \neq2$, temos que
$$f'(x)=0 \Leftrightarrow x=0 \ \ e \ \ f'(x)<0 ,\text{pois o denominador é positivo}$$Assim, a $f$ é estritamente decrescente em $[0,2)$ e em $(2,+\infty)$, logo não possui extremo local para $x\geq 0, x \neq2$, o único ponto que poderá ser máximo local é $x=0$ após termos o gráfico pronto.
Concavidade e inflexão:
$$=(-6) \ \dfrac{ \left(x^{2} - 4 \right)-4x^2}{\left(x^{2} - 4 \right)^{3}}=\dfrac{18x^2+24}{\left(x^{2} - 4 \right)^{3}}$$
O sinal da $f''$ é o mesmo de $x^2-4$, pois o denominador tem expoente ímpar e o numerador é sempre positivo. Logo,
$$f''(x)>0 \Leftrightarrow x\in (2,+\infty);\ \ f''(x)<0 \Leftrightarrow x\in [0,2).$$E, portanto, a $f$ tem concavidade para cima em $(2,+\infty)$ e para baixo em $[0,2)$. Não há ponto de inflexão, pois a troca de sinal da $f''$ ocorre em um ponto fora do domínio.
Agora, reunimos as informações obtidas e traçamos a metade do gráfico, para $x\geq 0, x \neq2$. Começamos com os pontos obtidos nos ítens acima: interseções com os eixos, extremos locais e inflexão.
Esboço da metade do gráfico:
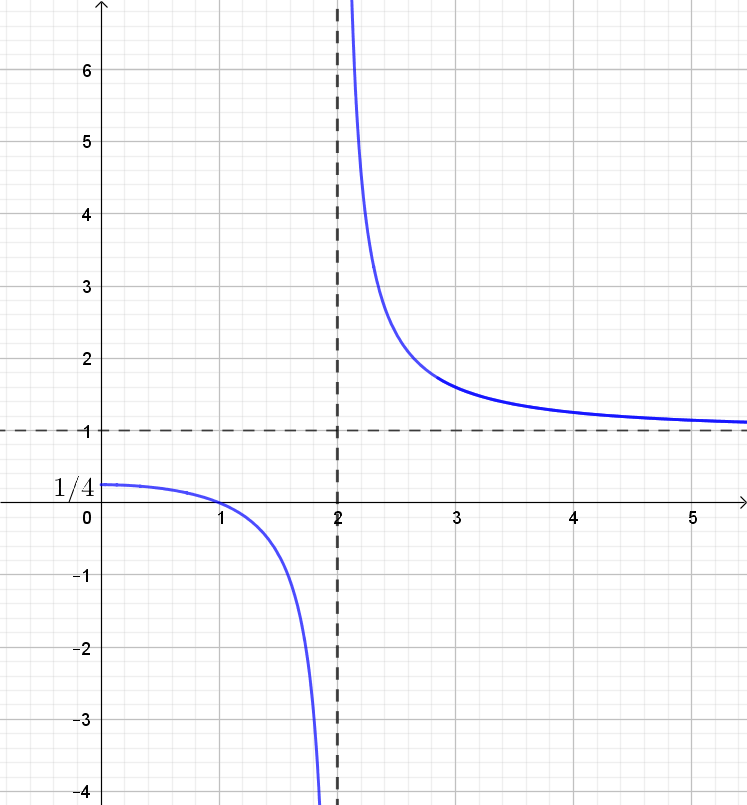
Esboço da metade do gráfico de $f(x)=\dfrac{x^2-1}{x^2-4}, x \neq 2 $.
Esboço do gráfico todo por simetria:
Após o esboço por simetria em relação ao eixo $y$, vemos que há duas assíntotas verticais $x=2$ e $x=-2$, há um máximo local em $x=0$. Não há extremos absolutos e o conjunto imagem $Im(f)=(-\infty,1/4]\cup (1,+\infty)$.
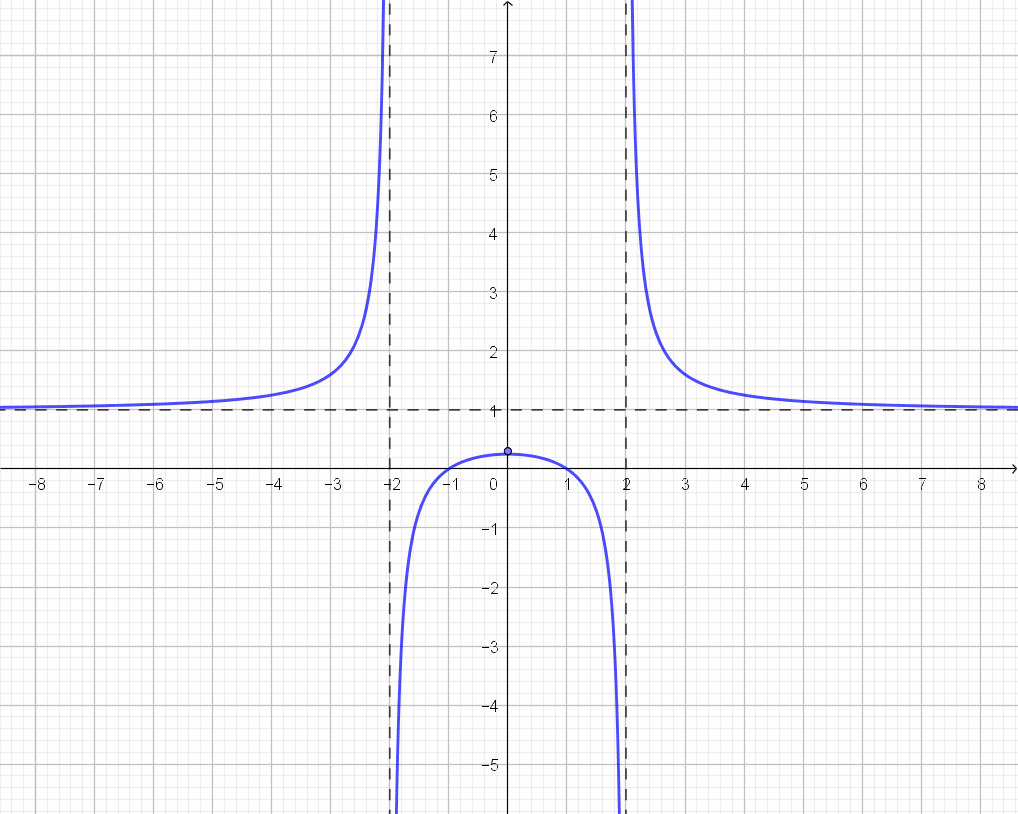
Esboço de todo o gráfico de $f(x)=\dfrac{x^2-1}{x^2-4}, x \neq \pm 2 $.
$f(x)=x^2e^x$
Domínio: $\mathbb{R}$
Interseções com os eixos:
Eixo $x$:
$f(x)=x^2e^x=0 \Leftrightarrow x=0 $, pois $e^x>0$. Ponto de interseção com os eixos $x$ e $y$: $(0,0)$.
A $f$ não é par e nem ímpar, por exemplo $f(-1)=1/e \neq \pm f(1)=e$.
Assíntotas horizontais:
$$ \displaystyle \lim_{x\to +\infty}x^2e^x=+\infty$$ $$ \displaystyle \lim_{x\to -\infty}x^2e^x \underset{ind[0.\infty]}{=}\lim_{x\to -\infty}\dfrac{x^2}{e^{-x}}\underset{[\frac{\infty}{\infty}, L'H}{=}\lim_{x\to -\infty}\dfrac{2x}{-e^{-x}}\underset{[\frac{\infty}{\infty}], L'H}{=}\lim_{x\to -\infty}\dfrac{2}{e^{-x}}=0.$$Logo, a reta $\boldsymbol{y=0}$ é uma assíntota horizontal.
Não há assíntotas verticais, pois a $f$ é contínua em $\mathbb{R}$.
Intervalos de crescimento/decrescimento e extremos locais:
Precisamos olhar o sinal da derivada de 1ª ordem da $f'(x)=2xe^x+x^2e^x=e^x(x^2+2x)$:
pois $e^x>0$. Assim, a $f$ é estritamente crescente em $(-\infty,-2)$ e em $(0,+\infty)$. É estritamente decrescente em $(-2,0)$, sendo $x=-2$ ponto de máximo local e $x=0$ de mínimo local da $f$. No gráfico, temos os pontos Máx$(-2,4e^{-2})$ e Mín$(0,0)$.
Concavidade e inflexão:
E, portanto, a $f$ tem concavidade para cima em $(-\infty, -2 - \sqrt{2})\cup (-2 + \sqrt{2}, +\infty);$ e para baixo em $(-2 -\sqrt{2},-2 + \sqrt{2})$, sendo, , $x= -2 \pm \sqrt{2}$ pontos de inflexão. Agora, reunimos as informações obtidas e colocamos no gráfico. Começamos com os pontos obtidos nos ítens acima: interseções com os eixos, extremos locais e inflexão.
Note que $4e^{-2}\approx 0,54$, $ (-2+\sqrt{2})^2e^{-2+\sqrt{2}}\approx 0,38$ e $(-2-\sqrt{2})^2e^{-2-\sqrt{2}}\approx 0,19$.
Esboço do gráfico: Após o esboço, vemos que o ponto de mínimo local é também absoluto, mas o de máximo é só local e $Im(f)=[0,+\infty).$
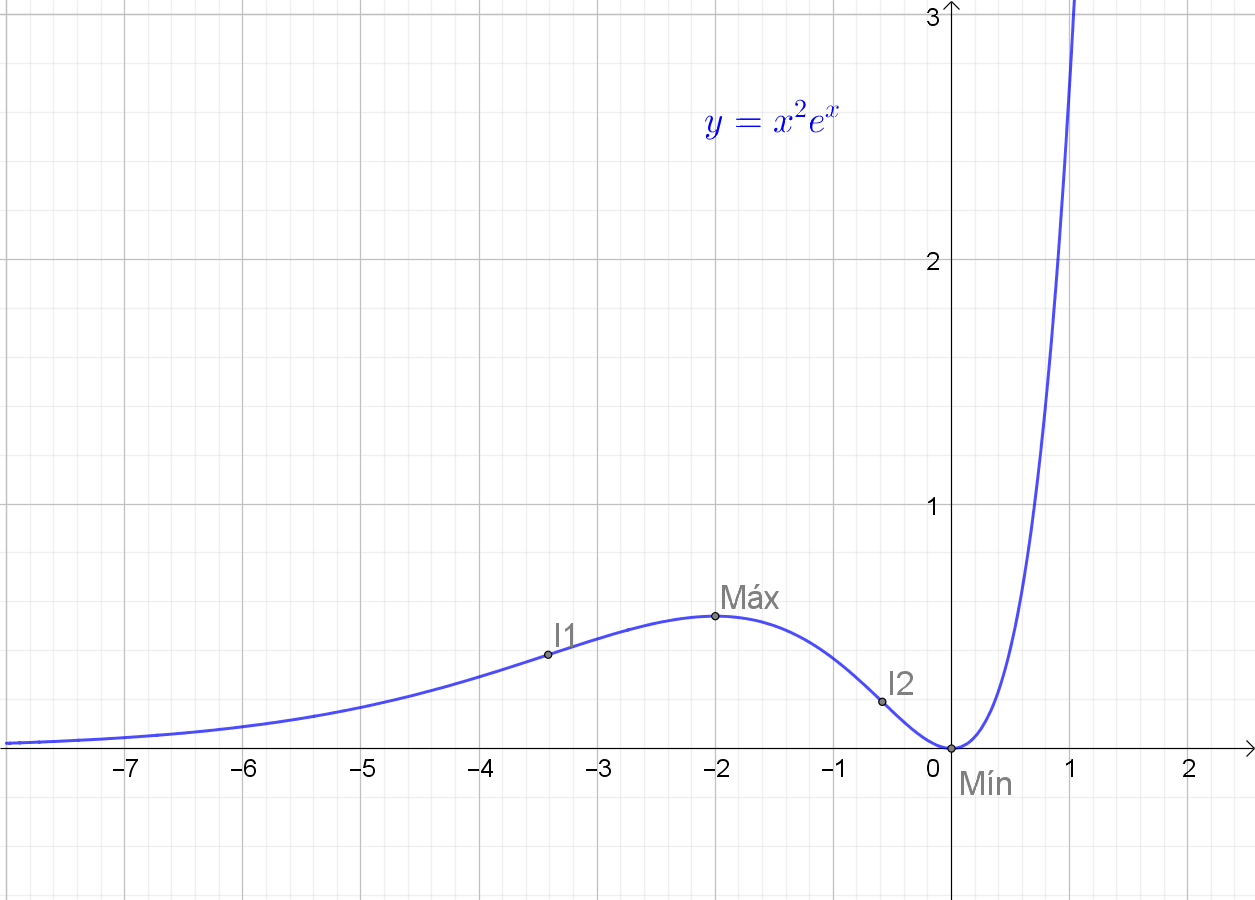
Esboço do gráfico de $f(x)=x^2e^x$; $I_1$ e $I_2$ pontos de inflexão no gráfico.
$f(x)=\dfrac{x}{\ln(x)}$
Domínio: Como $\mathrm{D}(\ln)=(0,+\infty)$ e o denominador não pode se anular, lembrando que $\ln(1)=0$, temos que $\mathrm{D}(f)=\{x\in \mathbb{R}; x>0 \ e \ x\neq1 \}$
Interseções com os eixos: Não possui, poi $0\notin \mathrm{D}(f)$.
Assíntota horizontal:
$$ \displaystyle \lim_{x\to +\infty}\dfrac{x}{\ln(x)}\underset{[\frac{\infty}{\infty}], L'H}{=}=\lim_{x\to +\infty}\dfrac{1}{\frac{1}{x}}=\lim_{x\to +\infty}x=+\infty$$Logo, não há assíntota horizontal no gráfico da $f$.
Assíntotas verticais: vamos procurar em $x=0$ e em $x=1$, pois são os pontos fora do domínio onde podemos calcular limites laterais que têm chance de serem infinitos. Neste caso,
$$\displaystyle \lim_{x\to 0^+}\dfrac{x}{\ln(x)}= \lim_{x\to 0^+}x \cancelto{0}{\dfrac{1}{\ln(x)}}=0$$ $$\displaystyle \lim_{x\to 1^-}\dfrac{x}{\ln(x)}=-\infty, \ \text{pois} \ \ln(x)\to 0^-$$ $$\displaystyle \lim_{x\to 1^+}\dfrac{x}{\ln(x)}=+\infty, \ \text{pois} \ \ln(x)\to 0^+$$Com os cálculos acima, sabemos o comportamento do gráfico quando nos aproximamos de $0$ pela direita e de $1$, tanto pela direita, como pela esquerda. Logo, a única assíntota vertical é a reta $x=1$.
Intervalos de crescimento/decrescimento e extremos locais:
Precisamos olhar o sinal da derivada de 1ª ordem da $f$:
Para $x> 0, x \neq1$, como $(\ln(x))^2>0$, temos que
$$f'(x)=0 \Leftrightarrow x=e; \ \ f'(x)>0 \Leftrightarrow x \in (e, +\infty) \ \ e \ \ f'(x)<0 \Leftrightarrow x\in (0,1)\cup(1,e)$$Assim, a $f$ é estritamente crescente em $(e, +\infty)$ e estritamente decrescente nos intervalos $(0,1)$ e $(1,e)$. O único extremo local ocorre em $x=e$ , sendo mínimo local(Não é absoluto, pois o domínio da $f$ não é um único intervalo. E de fato, foi visto que $f(x)\to -\infty$, se $x \to 1^-$.).
Concavidade e inflexão:
No Exemplo da página anterior, estudamos a concavidade dessa função, vimos que a concavidade é para cima em $(1,e^2)$ e para baixo em $(0,1) \cup (e^2,+\infty) $. Temos que $x=e^2$ é o único ponto de inflexão.
Agora, reunimos as informações obtidas e traçamos o gráfico.
Esboço do gráfico:
Após o esboço, vemos que o ponto de mínimo local não é absoluto e $Im(f)=(-\infty,0)\cup[e,+\infty)$.
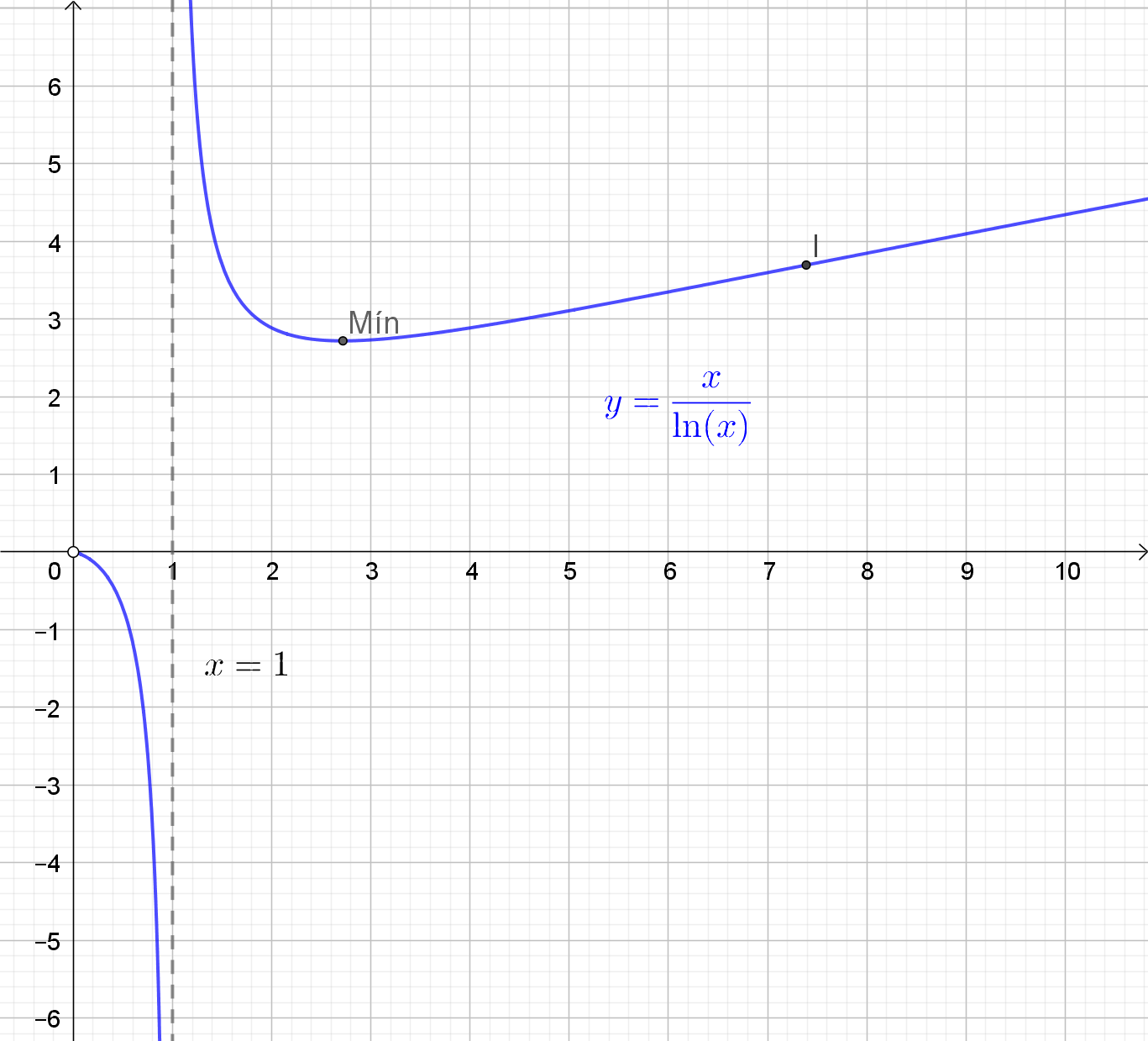
Esboço do gráfico de $f(x)=\dfrac{x}{\ln(x)}$; Mín é o ponto de mínimo local e $I$ é ponto de inflexão no gráfico.