
Considerando os gráficos de $g$ e $h$ dados, ache os limites laterais de $f$ no ponto indicado.
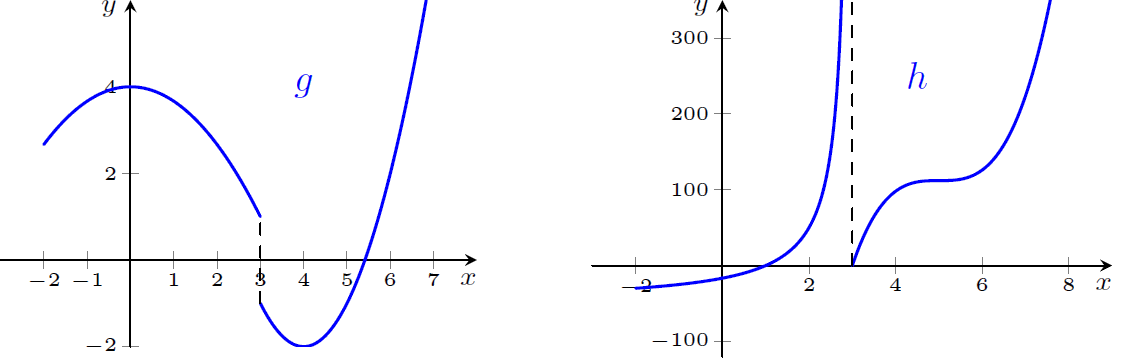
$f(x)=\dfrac{g(x)}{h(x)}$, no ponto $x=3$
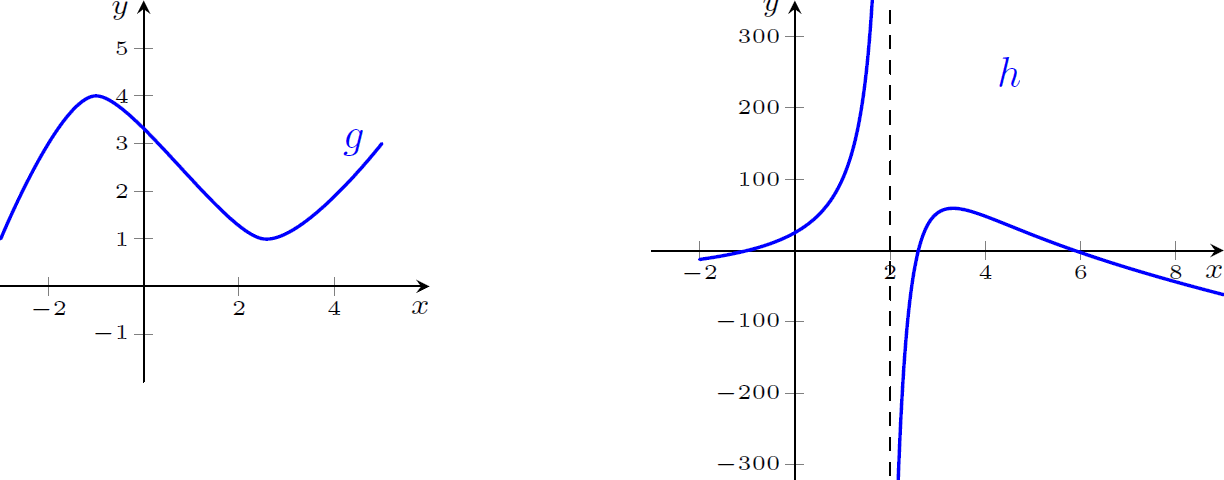
$f(x)=\dfrac{g(x)}{h(x)}$, no ponto $x=2$
$\displaystyle \lim_{x\rightarrow-3} f(x)=0$; $\displaystyle \lim_{x\rightarrow3^+}f(x)=-\infty$
$\displaystyle \lim_{x\rightarrow-2} f(x)=0$; $\displaystyle \lim_{x\rightarrow2^+}f(x)=0$
$\displaystyle \lim_{x \rightarrow 1^+} \frac{1}{|x-1|}$
$\displaystyle \lim_{x \rightarrow 3^-} \frac{2x+7}{(3-x)^2}$
$\displaystyle \lim_{x \rightarrow 5^-} \frac{x-5}{|x^2-7x+10|}$
$\displaystyle \lim_{x \rightarrow +\infty} \frac{(x+1)^2}{x}$
$\displaystyle \lim_{x \rightarrow -\infty} \sqrt[3]{x^5+3x-8}$
$\displaystyle \lim_{x \rightarrow +\infty} \frac{x-5}{x^2+3x+4}$
$\displaystyle \lim_{x \rightarrow -\infty} \frac{x-3}{7x+2}$
$\displaystyle \lim_{x \rightarrow +\infty} \frac{x^2-2}{3-x}$
$\displaystyle \lim_{x \rightarrow -\infty} \frac{x+2}{\sqrt{9x^2-3}}$
$\displaystyle \lim_{x \rightarrow -\infty} \frac{9x+3}{\sqrt[3]{8x^3-3}}$
$\displaystyle \lim_{x \rightarrow +\infty} \frac{\sqrt{x+\sqrt{x}}}{\sqrt{x+1}}$
$\displaystyle \lim_{x \rightarrow +\infty} x(\sqrt{x^2+5}-5)$
$\displaystyle \lim_{x \rightarrow -\infty} (\sqrt[3]{x^3+2}-\sqrt[3]{x^3-2})$
$\displaystyle \lim_{x\rightarrow1^+}\frac{1}{|x-1|}=\displaystyle \lim_{x\rightarrow1^+} \frac{1}{x-1}=+\infty$
$\displaystyle \lim_{x\rightarrow3-3}\frac{2x+7}{(3-x)^2}=+\infty$
Neste item temos uma indeterminação do tipo $\dfrac{0}{0}$, $\displaystyle \lim_{x\rightarrow5^-} \frac{x-5}{|x^2-7x+10|}=\displaystyle \lim_{x\rightarrow5^-} \frac{x-5}{|(x-2)(x-5)|}=\displaystyle \lim_{x\rightarrow5^-} \frac{-1}{x-2}=-\frac{1}{3}$
$\displaystyle \lim_{x\rightarrow+\infty}\frac{(x+1)^2}{x}=\displaystyle \lim_{x\rightarrow+\infty} \frac{x^2+2x+1}{x}=\displaystyle \lim_{x\rightarrow+\infty}x+2+\frac{1}{x}=+\infty$
$\displaystyle \lim_{x\rightarrow-\infty}\sqrt[3]{x^5+3x-8}=-\infty$
Nos itens 6-11 temos indeterminação do tipo $\dfrac{\infty}{\infty}$.
Nos itens 12 e 13, temos indeterminações do tipo $\infty-\infty$
$f(x)=\dfrac{3x}{x-1}$
$f(x)=\dfrac{2x}{\sqrt{x^2+4}}$
$f(x)=\dfrac{2x^2+1}{2x^2-3x}$
$\mathrm{D}(f)=\mathbb{R}\backslash\{1\}$
Assíntota horizontal: $y=3$, pois $\displaystyle \lim_{x\rightarrow-\infty}\frac{3x}{x-1}=3$ e $\displaystyle \lim_{x\rightarrow+\infty}\frac{3x}{x-1}=3$
$\mathrm{D}(f)=\mathbb{R}$
Assíntota horizontal: $y=-2$ e $y=2$, pois
$\mathrm{D}(f)=\mathbb{R}\backslash\{0,3/2\}$ Assíntota horizontal: $y=1$, pois $\displaystyle \lim_{x\rightarrow-\infty}\frac{2x^2+1}{2x^2-3x}=1$ e $\displaystyle \lim_{x\rightarrow+\infty}\frac{2x^2+1}{2x^2-3x}=1$ Assíntota vertical: $x=0$ e $x=\dfrac{3}{2}$, pois
$$\displaystyle \lim_{x\rightarrow0^-}\frac{2x^2+1}{2x^2-3x}=+\infty \text{ assim como } \displaystyle \lim_{x\rightarrow0^+}\frac{2x^2+1}{2x^2-3x}=-\infty$$ $$\text{e}$$ $$\displaystyle \lim_{x\rightarrow\dfrac{3}{2}^-}\frac{2x^2+1}{2x^2-3x}=-\infty \text{ assim como } \displaystyle \lim_{x\rightarrow\dfrac{3}{2}^+}\frac{2x^2+1}{2x^2-3x}=+\infty.$$Determine os valores de $a$ e $b$ de modo que
$$\displaystyle \lim_{x \rightarrow +\infty} \left(\frac{3x^2+bx-1}{x+2}-ax\right)=0$$$\displaystyle \lim_{x\rightarrow+\infty}\left(\frac{3x^2+bx-1}{x+2}-ax\right)=\displaystyle \lim_{x\rightarrow+\infty}\left(\frac{(3-a)x^2+(b-2x)x-1}{x+2}\right)=0 \iff \begin{cases} 3-a=0\\ b-2a=0 \end{cases} $
Seja $f$ a função dada pelo gráfico a seguir:
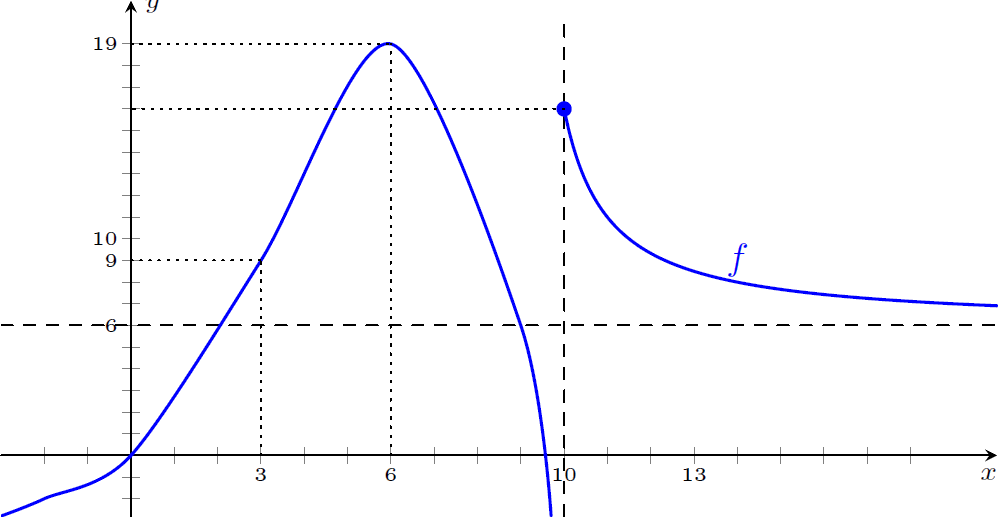
Baseando-se no gráfico de $f$, responda os seguintes itens:
$\displaystyle \lim_{x \rightarrow -\infty} f(x)$
$\displaystyle \lim_{x \rightarrow +\infty} f(x)$
$\displaystyle \lim_{x \rightarrow 10^-} f(x)$
$\displaystyle \lim_{x \rightarrow 10^+} f(x)$
Determine, caso existam, as equações das assíntotas verticais e horizontais deste gráfico.
$\displaystyle \lim_{x\rightarrow-\infty}f(x)=-\infty$
$\displaystyle \lim_{x\rightarrow+\infty}f(x)=6$
$\displaystyle \lim_{x\rightarrow10^-}f(x)=-\infty$
$\displaystyle \lim_{x\rightarrow10^+}f(x)=f(10)=16$
Assíntota horizontal: $y=6$.
Assíntota vertical: $x=10$.
Assumindo que $\displaystyle \lim_{x \rightarrow +\infty} \left(1+\frac{1}{x}\right)^x=e$, calcule os seguintes limites:
$\displaystyle \lim_{x \rightarrow +\infty} \left(1+\frac{1}{x}\right)^{4x}$
$\displaystyle \lim_{x \rightarrow +\infty} \left(1+\frac{3}{x}\right)^x$
$\displaystyle \lim_{x \rightarrow 0^+} \left(1+x\right)^\frac{1}{x}$
$\displaystyle \lim_{x \rightarrow 0^+} \left(1+x\right)^\frac{5}{x}$
$\displaystyle \lim_{x \rightarrow +\infty} \left(1+\frac{1}{x}\right)^{4x}=\displaystyle \lim_{x \rightarrow +\infty} \left(\left(1+\frac{1}{x}\right)^x\right)^4=e^4$
$\displaystyle \lim_{x \rightarrow +\infty} \left(1+\frac{3}{x}\right)^x=\displaystyle \lim_{x \rightarrow +\infty} \left(\left(1+\frac{1}{x/3}\right)^{x/3}\right)^3=\displaystyle \lim_{u \rightarrow +\infty} \left(\left(1+\frac{1}{u}\right)^u\right)^3=e^3$
$\displaystyle \lim_{x \rightarrow 0^+} \left(1+x\right)^\frac{1}{x}=\displaystyle \lim_{x \rightarrow 0^+} \left(1+\frac{1}{1/x}\right)^\frac{1}{x}=\displaystyle \lim_{u \rightarrow +\infty} \left(1+\frac{1}{u}\right)^u=e$
$\displaystyle \lim_{x \rightarrow 0^+} \left(1+x\right)^\frac{5}{x}=\displaystyle \lim_{x \rightarrow 0^+} \left(\left(1+\frac{1}{1/x}\right)^\frac{1}{x}\right)^5=\displaystyle \lim_{x \rightarrow 0^+} \left(\left(1+\frac{1}{u}\right)^u\right)^5=e^5$
Dê exemplos de funções $f$ e $g$ tais que
$\displaystyle \lim_{x \rightarrow 0^+} f(x)=0$, $\space$ $\displaystyle \lim_{x \rightarrow 0^+} g(x)=0$ $\space$ e $\space$ $\displaystyle \lim_{x \rightarrow 0^+} \frac{f(x)}{g(x)}=0$
$\displaystyle \lim_{x \rightarrow +\infty} f(x)=0$, $\space$ $\displaystyle \lim_{x \rightarrow +\infty} g(x)=0$ $\space$ e $\space$ $\displaystyle \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}=0$
$\displaystyle \lim_{x \rightarrow 0^+} \frac{f(x)}{g(x)}=+\infty$ $\space$ e $\space$ $\displaystyle \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}=1$
$\displaystyle \lim_{x \rightarrow 0^+} \frac{f(x)}{g(x)}=+\infty$ $\space$ e $\space$ $\displaystyle \lim_{x \rightarrow +\infty} \frac{f(x)}{g(x)}=0$
Se $f(x)=x$ e $g(x)=x^2$, teremos
$$\displaystyle \lim_{x\rightarrow0^+}f(x)=\displaystyle \lim_{x\rightarrow0^+}x=0 \text{, }\ \displaystyle \lim_{x\rightarrow0^+}g(x)=\displaystyle \lim_{x\rightarrow0^+}x^2=0 \text{ e } \displaystyle \lim_{x\rightarrow0^+}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow0^+}\frac{x}{x^2}=\displaystyle \lim_{x\rightarrow0^+}\frac{1}{x}=+\infty$$Se $f(x)=\frac{1}{x^2}$ e $g(x)=\frac{1}{x}$, teremos
$$\displaystyle \lim_{x\rightarrow+\infty}f(x)=\displaystyle \lim_{x\rightarrow+\infty}\frac{1}{x^2}=0 \text{, }\ \displaystyle \lim_{x\rightarrow+\infty}g(x)=\displaystyle \lim_{x\rightarrow+\infty}\frac{1}{x}=0 \text{ e } \displaystyle \lim_{x\rightarrow+\infty}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow+\infty}\frac{\frac{1}{x^2}}{\frac{1}{x}}=\displaystyle \lim_{x\rightarrow0^+}\frac{1}{x}=+\infty$$Se $f(x)=x+1$ e $g(x)=x$, teremos
$$\displaystyle \lim_{x\rightarrow0^+}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow0^+}\frac{x+1}{x}=+\infty \text{ e } \displaystyle \lim_{x\rightarrow+\infty}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow+\infty}\frac{x+1}{x}=1$$Se $f(x)=x+1$ e $g(x)=x^2$, teremos
$$\displaystyle \lim_{x\rightarrow0^+}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow0^+}\frac{x+1}{x^2}=+\infty \text{ e } \displaystyle \lim_{x\rightarrow+\infty}\frac{f(x)}{g(x)}=\displaystyle \lim_{x\rightarrow+\infty}\frac{x+1}{x^2}=0$$Calcule os limites abaixo
$\displaystyle \lim_{x \rightarrow 0} x \space \mathrm{sen}(x)$
$\displaystyle \lim_{x \rightarrow +\infty} \frac{4x^3+3x+\mathrm{sen}(x)}{3x^3-x^2}$
$\displaystyle \lim_{x\rightarrow -\infty} \frac{x^2+3x+2\mathrm{sen}(e^x)\mathrm{cos}(x)}{x^2+2x}$
Como $-1\leqslant\mathrm{sen}(x)\leqslant1$, temos
$$-|x|\leqslant\mathrm{sen}(x)\leqslant|x|$$, logo, como $\displaystyle \lim_{x\rightarrow0}-|x|=\displaystyle \lim_{x\rightarrow0}|x|=0,$ temos, pelo Teorema do Confronto,
$$\displaystyle \lim_{x\rightarrow0}x \space \mathrm{sen}(x)=0.$$Como $-1\leqslant\mathrm{sen}(x)\leqslant1$ então temos
$$4x^3+3x-1\leqslant4x^3+3x+\mathrm{sen}(x)\leqslant4x^3+3x+1$$Para $x$ suficientemente grande, $3x^3-x^2>0$, logo
$$\frac{4x^3+3x-1}{3x^3-x^2}\leqslant\frac{4x^3+3x+\mathrm{sen}(x)}{3x^3-x^2}\leqslant\frac{4x^3+3x+1}{3x^3-x^2}$$Como
$$\displaystyle \lim_{x\rightarrow+\infty}\frac{4x^3+3x-1}{3x^3-x^2}=\frac{4}{3} \text{ e } \displaystyle \lim_{x\rightarrow+\infty}\frac{4x^3+3x+1}{3x^3-x^2}=\frac{4}{3}$$temos, pelo Teorema do Confronto,
$$\displaystyle \lim_{x\rightarrow+\infty}\displaystyle \lim_{x\rightarrow+\infty}\frac{4x^3+3x+\mathrm{sen}}{3x^3-x^2}=\frac{4}{3}.$$Como $-1\leqslant\mathrm{sen}(e^x)\leqslant1$ e $-1\leqslant\mathrm{cos}(x)\leqslant1$, temos $-2\leqslant2\mathrm{sen}(e^x)\mathrm{cos}(x)\leqslant2$, logo
$$x^2+3x-2\leqslant x^2+3x+2\mathrm{sen}(e^x)\mathrm{cos}(x)\leqslant x^2+3x+2$$Para $x$ muito negativo, $x^2+2x>0$, logo
$$\frac{x^2+3x-2}{x^2+2x}\leqslant\frac{x^2+3x+2\mathrm{sen}(e^x)\mathrm{cos}(x)}{x^2+2x}\leqslant\frac{x^2+3x-2}{x^2+2x}$$Como
$$\displaystyle \lim_{x\rightarrow-\infty}\frac{x^2+3x-2}{x^2+2x}=1 \text{ e } \displaystyle \lim_{x\rightarrow-\infty}\frac{x^2+3x+2}{x^2+2x}=1$$Assim, pelo Teorema do Confronto,
$$\displaystyle \lim_{x\rightarrow-\infty}\frac{x^2+3x-2\mathrm{sen}(e^x)\mathrm{cos}(x)}{x^2+2x}=1$$Seja $f: \mathbb{R} \rightarrow \mathbb{R}$ tal que $-x^2+3x\leqslant f(x)<\dfrac{x^2-1}{x-1}$ para todo $x\neq1$. Diga se existe $\displaystyle \lim_{x\rightarrow1} f(x)$ e calcule este limite, caso exista.
Temos que
$$-x^2+3x\leqslant f(x)\leqslant\frac{x^2-1}{x-1}.$$Ainda mais,
$$\displaystyle \lim_{x\rightarrow1}-x^2+3x=2 \text{ e } \displaystyle \lim_{x\rightarrow1}\frac{x^2-1}{x-1}=\displaystyle \lim_{x\rightarrow1}\frac{(x-1)(x+1)}{x-1}=\displaystyle \lim_{x\rightarrow1}(x+1)=2.$$Logo, pelo Teorema do Confronto,
$$\displaystyle \lim_{x\rightarrow1}f(x)=2.$$Seja $f: \mathbb{R} \rightarrow \mathbb{R}$ tal que $|f(x)-3| \leqslant 2|x-1|$ para todo $x\in\mathbb{R}$. Calcule $\displaystyle \lim_{x\rightarrow1} f(x)$, caso exista.
Como $|f(x)-3|\leqslant2|x-1|$, temos
$$-2|x-1|\leqslant f(x)-3\leqslant2|x-1|.$$Como
$$\displaystyle \lim_{x\rightarrow1}-2|x-1|=0 \text{ e } \displaystyle \lim_{x\rightarrow1}2|x-1|=0$$pelo Teorema do Confronto, temos
$$\displaystyle \lim_{x\rightarrow1}(f(x)-3)=0.$$Com isso,
$$\displaystyle \lim_{x\rightarrow1}f(x)=3$$Seja $f: \mathbb{R} \rightarrow \mathbb{R}$ tal que $|f(x)|\leqslant x^4$ para todo $x\in\mathbb{R}$. Calcule $\displaystyle \lim_{x\rightarrow0}\frac{f(x)}{x}$.
Como $0\leq|f(x)|\leq x^4$ então, para $x\neq0$ temos
$$0\leq\left|\frac{f(x)}{x}\right|\leq\frac{x^4}{|x|}=|x^3|.$$Portanto
$$-|x^3|\leq\left|\frac{f(x)}{x}\right|=|x^3|.$$e assim temos
$$-|x|^3\leq\frac{f(x)}{x}\leq|x|^3.$$Como $\displaystyle \lim_{x\rightarrow0}-|x|^3=0$ e $\displaystyle \lim_{x\rightarrow0}|x|^3=0$. Então, pelo Teorema do Confronto, temos
$$\displaystyle \lim_{x\rightarrow0}\frac{f(x)}{x}=0.$$Seja $f: \mathbb{R} \rightarrow \mathbb{R}$ tal que $|f(x)|\leqslant x^3$ para $x\in[0,+\infty)$. Para que valores de $k\in\mathbb{R}$ podemos garantir que $\displaystyle \lim_{x\rightarrow0^+} \frac{f(x)}{x^k}=0$?
Como $|f(x)|\leqslant x^3$, temos que $-x^3\leqslant f(x)\leqslant x^3$ para $x\in[0,+\infty)$. Assim,
$$-\frac{x^3}{x^k}\leqslant\frac{f(x)}{x^k}\leqslant\frac{x^3}{x^k}$$Se $k<3$ então $0<3-k$ e assim teremos que
$$\displaystyle \lim_{x\rightarrow0^+}-\frac{x^3}{x^k}=-\displaystyle \lim_{x\rightarrow0^+}x^{3-k}=0 \text{ e } \displaystyle \lim_{x\rightarrow0^+}\frac{x^3}{x^k}=\displaystyle \lim_{x\rightarrow0^+}x^{3-k}=0.$$Assim, pelo Teorema do Confronto, temos
$$\displaystyle \lim_{x\rightarrow0^+}-\frac{f(x)}{x^k}=0.$$Se $k=3$, não podemos garantir que $\lim_{x\rightarrow0^+}\frac{f(x)}{x^k}=0$. Por exemplo, se tivermos $f(x)=x^3$, a condição $|f(x)|\leqslant x^3$ será válida e $\displaystyle \lim_{x\rightarrow0^+}\frac{f(x)}{x^3}=-\displaystyle \lim_{x\rightarrow0^+}\frac{x^3}{x^3}=1$ Da mesma forma, se $k>3$, tomando novamente $f(x)=x^3$, temos
$$\displaystyle \lim_{x\rightarrow0^+}\frac{f(x)}{x^k}=\displaystyle \lim_{x\rightarrow0^+}\frac{x^3}{x^k}=\displaystyle \lim_{x\rightarrow0^+}x^{3-k}=+\infty.$$Portanto, o limite nulo só é garantido quando $k<3$.