
Em cada um dos exercícios abaixo verifique se a função $f$ é contínua no ponto $a$ indicado:
$a = 2$ e $\displaystyle f(x) = \begin{cases} \frac{x^2+x-6}{x-2} & \text{se } x<2 \\ 5 & \text{se } x=2 \\ \mathrm{sen} (x^2-4) & \text{se } x>2 \end{cases} $
$a = 3$ e $\displaystyle f(x) = \begin{cases} \frac{|x^2 -4x+3|}{x-3} & \text{se } x\neq 3 \\ 1 & \text{se } x=3 \end{cases} $
Para verificar a continuidade de $f$ no ponto $a$ indicado devemos verificar se $\displaystyle \lim_{x \to a}f(x)=f(a)$.
Não, pois $\displaystyle \lim_{x \to 2^+} \mathrm{sen} (x^2-4)= \mathrm{sen} (0)= 0 \neq 5 =f(2)$.
Não, pois
$$\lim_{x \to 3^-} \frac{|x^2 -4x+3|}{x-3}=\lim_{x \to 3^-} \frac{|(x-3)(x-1)|}{x-3}=\lim_{x \to 3^-} -\frac{(x-3)(x-1)}{x-3} \\ =\lim_{x \to 3^-} -(x-1)=-2 \neq 1=f(3)$$Determine os valores de $k$ que tornam cada uma das funções abaixo contínuas.
$\displaystyle f(x) = \begin{cases} \dfrac{x^2-1}{x+1} & \text{se } x<-1 \\ ax+b & \text{se } -1\leqslant x\leqslant 1 \\ \dfrac{\mathrm{sen}(3x)}{x} & \text{se } x>0 \end{cases} $
$\displaystyle f(x) = \begin{cases} \dfrac{|x+2|}{x+2} & \text{se } x<2 \text{ ou } x>0 \\ ax^2+b & \text{se } -2\leqslant x\leqslant0 \end{cases} $
$\displaystyle f(x) = \begin{cases} \dfrac{\mathrm{sen}(b(x-2))}{|x-2|} & \text{se } x<2 \\ ax & \text{se } 2\leqslant x\leqslant 4 \\ \dfrac{x^2-9x+20}{x-4} & \text{se } x>4 \end{cases} $
Precisamos descobrir $a$ e $b$ para que
$$\displaystyle \lim_{x\to-1} f(x)=f(-1) \text{ e } \displaystyle \lim_{x\to0} f(x)=f(0).$$Como
$$\displaystyle \lim_{x\to1^-} f(x)=\displaystyle \lim_{x\to1^-}\frac{x^2-1}{x+1}=\displaystyle \lim_{x\to1^-}=\frac{(x+1)(x-1)}{x+1}=\displaystyle \lim_{x\to1^-} x-1=-2,$$precisamos ter $-2=f(-1)=a\cdot(-1)+b=b-a$.
Por outro lado, como
precisamos ter $3=f(0)=a\cdot0+b$, logo $b=3$. Como já sabemos que $b-a=-2$, temos $3-a=-2$, logo $a=5$.
Queremos
$$\displaystyle \lim_{x\to-2} f(x)=f(-2) \text{ e } \displaystyle \lim_{x\to0}f(x)=f(0).$$Como
$$\displaystyle \lim_{x\to-2^-} f(x)=\displaystyle \lim_{x\to-2^-} \frac{|x+2|}{x+2}=\displaystyle \lim_{x\to-2^-} \frac{-(x+2)}{x+2}=-1,$$precisamos ter $-1=f(-2)=a\cdot(-2)^2+b=4a+b$.
Por outro lado, como
precisamos ter $1=f(0)=a\cdot0^2+b=b$. Logo, $b=1$.
Como já tínhamos $4a+b=-1$, temos $4a+1=-1$, logo $4a=-2$ e então $a=-\frac{1}{2}$.
Queremos
$$\displaystyle \lim_{x\to2} f(x)=f(2) \text{ e } \displaystyle \lim_{x\to4}f(x)=f(4).$$Como
$$\displaystyle \lim_{x\to2^-}f(x)=\displaystyle \lim_{x\to2^-}\frac{\mathrm{sen}(b(x-2))}{|x-2|}=\displaystyle \lim_{x\to-2^-}\frac{\mathrm{sen}(b(x-2))}{-|x-2|}=\displaystyle \lim_{x\to-2^-}b\cdot\frac{\mathrm{sen}(b(x-2))}{-b(x-2)}=-b,$$precisamos ter $-b=f(2)=2a$, logo $b=-2a$.
Por outro lado, como
precisamos ter $-1=f(4)=4a$. Logo, $a=-\frac{1}{4}$.
Como já tínhamos $b=-2a$, temos $b=-2\cdot(-\frac{1}{4})$, logo $b=\frac{1}{2}$
Para cada função $g$ definida nos itens abaixo, diga se existe uma função $f:\mathbb{R}\rightarrow\mathbb{R}$, contínua em $\mathbb{R}$ tal que $f(x)=g(x)$ para todo $x$ no domínio de $g$. Caso seja possível, dê a expressão da função $f$
$\displaystyle g(x) =\begin{cases} \dfrac{\mathrm{sen}(3x-3)}{x-1}&\text{se }x < 1\\ \dfrac{x^2 +x-2}{x-1}, &\text{se }x > 1 \end{cases} $
$\displaystyle g(x) = \frac{|x-3|}{x-3}$
[1.] Observe que $g$ é contínua em $\mathbb{R}-\{1\}$. Temos ainda que
\[\displaystyle \lim_{x\to 1^-} g(x) = \lim_{x\to 1^-} \frac{\mathrm{sen}(3x-3)}{x-1} = \lim_{x\to 1^-} \frac{\mathrm{sen}(3(x-1))}{x-1} = \lim_{x\to 1^-} 3\cdot \cancelto{1}{\frac{\mathrm{sen}(3(x-1))}{3(x-1)}} = 3.\] \[\displaystyle \lim_{x\to 1^+} g(x) = \lim_{x\to 1^+} \dfrac{x^2 +x-2}{x-1} = \lim_{x\to 1^+} \dfrac{(x+2)(x-1)}{x-1} = \lim_{x\to 1^+} (x+2) = 3.\]Assim, $\displaystyle \lim_{x\to 1} g(x)= 3$. Definindo
\[f(x) =\begin{cases} \dfrac{\mathrm{sen}(3x-3)}{x-1}&\text{se }x < 1\\ 3,&\text{se }x=1\\\dfrac{x^2+x-2}{x-1}, &\text{se }x > 1 \end{cases} ,\]temos $f$ contínua em $\mathbb{R}$. A continuidade em $x=1$ vem de
\[\displaystyle \lim_{x\to 1} f(x) = \displaystyle \lim_{x\to 1} g(x) = 3 = f(1).\][2.] Observe que $g$ é contínua em $\mathbb{R}-\{3\}$. Temos ainda que
\[\displaystyle \lim_{x\to 3^-} g(x) = \lim_{x\to 3^-} \frac{|x-3|}{x-3} \underset{x-3<0}{=} \lim_{x\to 3^-} \frac{-(x-3)}{x-3} = -1,\] \[\displaystyle \lim_{x\to 3^+} g(x) = \lim_{x\to 3^+} \frac{|x-3|}{x-3} \underset{x-3>0}{=} \lim_{x\to 3^+} \frac{x-3}{x-3} = 1,\]portanto, não podemos definir um valor para $f(3)$ de forma a termos $\displaystyle \lim_{x\to 3} f(x) = f(3)$, pois $\displaystyle \lim_{x\to 3} f(x) = \displaystyle \lim_{x\to 3} g(x)$, que não existe.
Sejam $f$, $g$ e $h$ funções com domínio $\mathbb{R}$, representadas pelos gráficos abaixo.
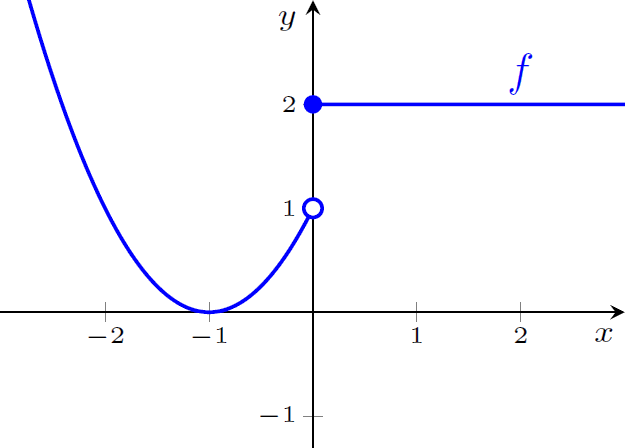


Verifique se as funções $fg$ e $h \circ g$ são contínuas em $x=0$.
Pelos gráficos podemos verificar que $\displaystyle \lim_{x \to 0^+} f(x)=2$, $\displaystyle \lim_{x \to 0^-} f(x)=1$, $\displaystyle \lim_{x \to 0^+} g(x)=1$ e $\displaystyle \lim_{x \to 0^-} g(x)=2$. Então
$$ \lim_{x \to 0^+} (fg)(x)= \left(\lim_{x \to 0^+} f(x)\right)\left(\lim_{x \to 0^+} g(x)\right)=2 \quad \text{e} \quad \lim_{x \to 0^-} (fg)(x)= \left(\lim_{x \to 0^-} f(x)\right)\left(\lim_{x \to 0^-} g(x)\right)=2.$$ Além disso, $(fg)(0)=2 \cdot 1=2$. Logo, $fg$ é contínua em $x=0$.
Para verificar se $h \circ g$ é contínua em $0$, precisamos observar que quando $x$ tende para $0^-$ então $g(x)$ tende para $2^-$ (pela esquerda) e quando $x$ tende para $0^+$ então $g(x)$ tende para $1^-$ (pela esquerda). Logo
Além disso $(h \circ g)(0)=h(1)=1$. Portanto $h \circ g$ é contínua em $0$.
Seja $f: \mathbb{R}\rightarrow\mathbb{R}$, tal que $x^2\cos^2(x)\leq f(x)\leq x \space \mathrm{sen}(x), \forall \in \left(-\frac{\pi}{2},\frac{\pi}{2}\right)$. Verifique se $f$ é contínua em $x=0$.
Temos que $ \lim_{x \to 0}x^2 \cos (x)=0$ e $ \lim_{x \to 0} x \mathrm{sen} (x)=0$, logo, pelo Teorema do Confronto, obtemos $ \lim_{x \to 0} f(x)=0$. Além disso $f(0)=0$, pois se substituirmos $x$ por $0$ nas desigualdades $ x^2 \cos^2 (x) \leq f (x) \leq x \mathrm{sen}(x)$, obtemos $0 \leq f(x) \leq 0$. Portanto $f$ é contínua em $x=0$.
Diga se cada afirmação é verdadeira ou falsa, justificando quando verdadeira e dando contraexemplo quando falsa.
Se $f$ e $g$ são contínuas em $\mathbb{R}$ e $a\in\mathbb{R}$, então
\[\displaystyle \lim_{x\to a} f\circ g(x) = f\left(\lim_{x\to a} g(x)\right) = f\left(g(a)\right).\]Se $f$ e $g$ são funções $\mathbb{R}\rightarrow\mathbb{R}$, com $f$ contínua em $\mathbb{R}$ e $g$ descontínua em pelo menos um ponto, então $f\circ g$ é necessariamente descontínua em pelo menos um ponto?
Sejam $f$ e $g$ funções $\mathbb{R}\rightarrow\mathbb{R}$. Se $f$ é descontínua em $x=1$, $g$ é contínua em $x=0$ e $g(0)=1$, então $f\circ g$ é necessariamente descontínua em $x=0$?
Como $g$ é contínua em $\mathbb{R}$, será contínua em $x=a$, logo $\displaystyle \lim_{x\to a} g(x) = g(a)$. Com isso,
$$\displaystyle \lim_{x\to a} f\circ g(x) = f\left(\lim_{x\to a} g(x)\right) = f\left(g(a)\right).$$Além disso, como $f$ é contínua, temos em particular que $f$ é contínua em $g(a)$, assim, pelo Teorema visto sobre a continuidade da composta, temos
$$\displaystyle \lim_{x\to a} f\circ g(x) = f(g(a)).$$Falso. Qualquer que seja a função $g$, se $f$ for uma função constante, isto é, $f(x) = a \in \mathbb{R}$, teremos $f\circ g(x) = a$ para todo $x\in\mathbb{R}$. Logo $f\circ g$ é contínua.
Falso. Podemos tomar
\[f(x) = \begin{cases} 1& \text{se }x \geqslant 1\\0&\text{se }x < 1 \end{cases} \;\;\;g(x) = 1+x^2.\]Estas funções satisfazem às condições informadas, e
\[f\circ g(x) = f(1+x^2) = 1,\]pois $1+x^2 \geq 1$ para todo $x \in \mathbb{R}$. Temo então $f\circ g(x) = 1$, logo $f\circ g$ é contínua em $x=0$.
Considere a função $f$ definida por $f(x)=x^3-4x^2+5$. Mostre que $f(x)=10$ tem pelo menos uma solução no intervalo $(4,5)$.
Temos que $f$ é contínua em $\mathbb{R}$. Como $f(4)=5$ e $f(5)=30$, então pelo TVI, existe $x \in (4,5)$ tal que $f(x)=10$.
Seja $f$ uma função contínua, de domínio $[0,5]$ e contradomínio $[3,4]$. Seja $g$ a função de domínio $[0,5]$, definida por $g(x)=f(x)-x$. Prove que a função $g$ tem, pelo menos, um zero.
A função $g(x) = f(x) - x$ é contínua em $[0,5]$. Como $g(0)=f(0)-0=f(0) \in [3,4]$ e $g(5)=f(5)-5 \in [-2,-1]$, então $g(0)>0$ e $g(5)<0$. Assim, pelo TVI, existe $x \in [0,5]$ tal que $g(x) = 0$.
Para cada função abaixo determine um intervalo de amplitude $1$, no qual está localizado pelo menos um zero dessa função.
$f (x) = x^3 + x-1$
$\displaystyle f (x) = 1 + x \cos\left(\frac{\pi x}{2}\right)$
A função $f$ é contínua, pois é um polinômio. Como $f(0)=-1<0$ e $f(1)=1>0$, pelo TVI, existe pelo menos um zero de $f$ no intervalo $(0,1)$.
A função $f$ é contínua, por ser a soma de uma constante com uma função trigonométrica. Como $f(1)=1>0$ e $f(2)=-1<0$, pelo TVI, existe pelo menos um zero de $f$ no intervalo $(1,2)$.
Mostre que os gráficos de $y = 1$ e $y = x^2 \tan (x)$ têm interseção em pelo menos um ponto do intervalo $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$.
Considere a função $\displaystyle f(x)=x^2 \tan (x)$. Temos que a função $f$ é contínua em $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$,
$$ \lim_{x\to \left(-\frac{\pi}{2}\right)^+}f(x)=-\infty \quad \text{e} \quad \lim_{x\to\left(\frac{\pi}{2}\right)^-}f(x)=+\infty.$$Logo pelo TVI, a função $f$ admite um zero no intervalo $\left(-\frac{\pi}{2}, \frac{\pi}{2} \right)$, ou seja, exsite $x_1 \in \left(-\frac{\pi}{2}, \frac{\pi}{2} \right)$ tal que $f(x_1)=1$.
Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado.
$\mathrm{sen}(x) = x-1$, $\left(\frac{\pi}{2},\pi\right)$
$x^2=\sqrt{x+1}$, $(1,2)$
$\ln x=e^{-x}$, $(1,2)$
Defina $f(x) = x^2-\sqrt{x+1}$. Temos que $f$ é contínua em $[1,2]$ (o único problema à continuidade seria a raiz não estar definida, mas $x+1\geqslant 0$ para todo $x \in [1,2]$). Temos ainda $f(1) = 1 - \sqrt{2} < 0$, $f(2) = 4 - \sqrt{3} > 0$. Assim, $f(1) < 0 < f(2)$, logo, pelo TVI, existe $x \in (1,2)$ tal que $f(x) = x^2 - \sqrt{x+1} = 0$, logo $x^2=\sqrt{x+1}$.
Defina $f(x) = \mathrm{sen}(x) - x + 1$. Temos que $f$ é contínua em $\left(\frac{\pi}{2},\pi\right)$, $f\left(\frac{\pi}{2}\right) = 1 - \frac{\pi}{2}+1 = 2-\frac{\pi}{2}>0$ e $f\left(\pi\right) = 0 - \pi + 1 < 0$. Assim, $f\left(\pi\right) < 0 < f\left(\frac{\pi}{2}\right)$, logo, pelo TVI, existe $x \in \left(\frac{\pi}{2},\pi\right)$ tal que $f(x) = \mathrm{sen}(x) - x + 1 = 0$, logo $\mathrm{sen}(x) = x - 1$.
Defina $f(x) = \ln x - e^{-x}$. Temos que $f$ é contínua em $[1,2]$ (o único problema à continuidade seria $\ln$ não estar definida, mas $x \geqslant 1 > 0$). Temos ainda $f(1) = -e^{-1} < 0$, $f(2) = \ln 2 - e^{-2} > 0$. Assim, $f(1) < 0 < f(2)$, logo, pelo TVI, existe $x \in (1,2)$ tal que $f(x) = \ln x - e^{-x} = 0$, logo $\ln x = e^{-x}$.
De uma função $f$, contínua em $\mathbb{R}$, sabe-se que: $1$ é zero de $f$, e $f(3)>0$. Prove que a equação $\displaystyle f(x)=\frac{f(3)}{2}$ tem, pelo menos, uma solução no intervalo $(1,3)$.
Considere a função $\displaystyle g(x)=f(x)-\frac{f(3)}{2}$. Temos que a função $g$ é contínua em $\mathbb{R}$, $\displaystyle g(1)=f(1)-\frac{f(3)}{2}=-\frac{f(3)}{2}<0$ e $\displaystyle g(3)=f(3) -\frac{f(3)}{2} = \frac{f(3)}{2} > 0$. Logo pelo TVI, a função $g$ admite um zero no intervalo $(1,3)$, ou seja, existe $x_1 \in (0,3)$ tal que $g(x_1)=0$. Mas então $\displaystyle f(x_1)=\frac{f(3)}{2}$.
Considere uma função $f$ contínua no intervalo $[a,b)$, com $f(a)=M$ e $\displaystyle \lim_{x\to b^-}f(x)=+\infty$. Dado $N > M$, podemos afirmar que existe $c\in[a,b)$ tal que $f(c)=N$?
Sim. Seja $N > M$. Como $\displaystyle \lim_{x\to b^-}f(x)=+\infty$, existe $b' < b$, próximo a $b$ tal que $f(b') > N$. Assim, $f(a) = M < N < f(b')$, com $f$ contínua em $[a,b']$, logo, pelo TVI, existe $c\in(a,b')\subset (a,b)$ tal que $f(c)=N$.
Seja $f(x)$ uma função contínua em $\mathbb{R}$ sobre a qual se sabe:
$\displaystyle \lim_{x\rightarrow -\infty} f(x) = -2$.
$\displaystyle \lim_{x\rightarrow \infty} f(x) = 4$
$f(3) = 5$
$f$ é negativa em $(1,2) \cup (4,6)$
$f(-2) = 3$.
Quantas soluções tem, no mínimo, $f(x) = 1$?
Como $\lim_{x\to-\infty} f(x) = -2$, temos que $f(x)$ é arbitrariamente próximo de $-2$ para $x$ muito negativo. Em particular, existe $x_0 < -2$ tal que $f(x_0) < 1$. Assim, $f$ é contínua em $[x_0, -2]$ e $f(x_0) < 1 < 3 = f(-2)$, logo, pelo TVI, existe pelo menos uma solução para $f(x)=1$ em $(x_0, -2)$.
Como $f$ é negativa em $(1,2)$, podemos tomar $x_1 \in (1,2)$ tal que $f(x_1) < 0$. Então, como $f$ é contínua em $[-2,x_1]$, e como $f(x_1) < 0 < 1 < 3 = f(-2)$ , pelo TVI $f(x)=1$ tem pelo menos uma solução em $(-2,x_1)$.
Da mesma forma, como $f(x_1) < 0 < 1 < 5 = f(3)$, $f(x)=1$ tem pelo menos uma solução em $(x_1,3)$.
Tomando $x_2 \in (4,6)$, temos $f(x_2) < 0$, logo $f(x_2) < 0 < 1 < 5 = f(3)$, logo $f(x)=1$ tem pelo menos uma solução em $(x_2, 3)$.
Como $\lim_{x\to\infty} f(x) = 4$, temos que $f(x)$ é arbitrariamente próximo de $4$ para $x$ muito grande. Em particular, existe $x_3 > 6$ tal que $f(x_3)> 3$. Assim, $f$ é contínua em $[x_2, x_3]$ e $f(x_2) < 0 < 1 < f(x)$, logo, pelo TVI, existe pelo menos uma solução de $f(x)=1$ em $(x_2, x_3)$.
Concluimos que $f(x) = 1$ tem pelo menos 5 soluções.
Dê um exemplo de uma função tal que que em dois pontos distintos $x = a$ e $x = b$ a função tem sinais contrários, $f$ não é contínua no intervalo $[a,b]$ e a tese do Teorema do Valor Intermediário é verdadeira.
Dê um exemplo de uma função tal que que em dois pontos distintos $x = a$ e $x = b$ a função tem sinais contrários, $f$ não é contínua no intervalo $[a,b]$ e a tese do Teorema do Valor Intermediário é falsa.
Há infinitas possibilidades!
Apresentamos uma abaixo.
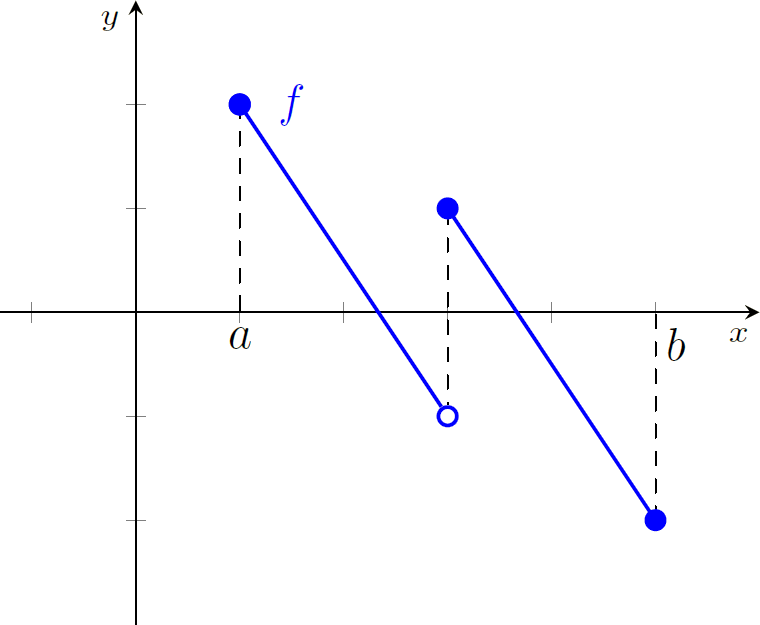
Há infinitas possibilidades!
Apresentamos uma abaixo.
