
Uma função $f$ é dita diferenciável em um ponto $x_0$ do seu domínio, se existe um número real $a\in\mathbb{R}$ tal que:
\begin{equation}\tag{1}\left\{ \begin{aligned} &f(x) = f(x_0) + a(x-x_0) + erro(x), \\[0.1cm]&erro(x_0) = 0, \\[0.1cm]&\lim_{x \rightarrow x_0}\frac{erro(x)}{x-x_0} = 0. \end{aligned} \right.\end{equation}Quando esse número real existe, ele é dito a derivada de $f$ em $x_0$ e escrevemos $f'(x_0) = a$.
Use a definição 1 para resolver os problemas a seguir.
Dada a função $f(x) = 3x^3 +2x$, verifique que $f'(1) = 11$.
Dada a função $f(x) = \mathrm{sen}(x)$, verifique que $f'(0) = 1$.
De acordo com a definição, escrevemos $f(x) = f(1) + a(x-1) + erro(x)$ em que $a$ é nosso candidato a $f'(1)$. A derivada no ponto $x=1$ será $a$ se e somente se:
\[\displaystyle\lim_{x\rightarrow 1} \frac{erro(x)}{x-1} = 0.\]Usando a função do enunciado e $a=11$ escrevemos:
\begin{equation}\tag{2}3x^3+2x = 5 + 11(x-1) + erro(x).\end{equation}De 2 concluímos:
\begin{equation}erro(x) = 3x^3+2x -5 -11(x-1) = 3(x^3-3x+2).\end{equation}Precisamos, então, fazer o limite:
\[ \displaystyle \lim_{x \rightarrow 1}\frac{3(x^3-3x+2)}{x-1}. \]Calculando:
\[\displaystyle \lim_{x \rightarrow 1}\frac{3(x^3-3x+2)}{x-1} =\displaystyle \lim_{x \rightarrow 1}\frac{3(x-1)(x^2+x-2)}{x-1}= \displaystyle \lim_{x \rightarrow 1} 3(x^2+x-2) =0.\]E, portanto, $f'(1) = 11$.
Procedendo como no exercício anterior, escrevemos:
\[\sin(x) = \sin(0) + 1 \cdot x + erro(x)= x +erro(x).\]Precisamos mostrar:
\[\displaystyle\lim_{x\rightarrow 0} \frac{\sin(x)-x}{x} = 0.\]Calculando:
\[\displaystyle\lim_{x\rightarrow 0} \frac{\sin(x)-x}{x}= \lim_{x\rightarrow 0}{\frac{\sin x}{x}} -1=0.\]Use a defini\ccao em 1 para resolver esse exercício. Seja $f(x)$ uma \fc real, diferenciável em $\mathbb R$, tal que $f(1) =2 $ e $f'(1) = \pi$. Calcule
\[\displaystyle \lim_{x \rightarrow 1}\frac{f(x) - 2}{x-1}\]Aplicando 1 em $x_0=1$ temos que
$$f(x)=f(x_0)+ f'(x_0)(x-x_0)+erro(x)=2+\pi(x-1)+erro(x).$$Daqui obtemos que
$$\frac{f(x)-2}{x-1}=\pi + \frac{erro(x)}{x-1}.$$Então tomando limite quadno $x\to 1$ chegamos em
$$\lim_{x\to 1} \frac{f(x)-2}{x-1}= \pi + \lim_{x\to 1} \frac{erro(x)}{x-1}=\pi.$$Use a definição em 1 para resolver esse exercício. Seja $f(x)$ uma função tal que
\[f(0) = \sqrt{2} \qquad \text{e} \qquad f(x) =\sqrt{2} + 5x +h(x).\]Sabe-se que
\begin{equation}\displaystyle\lim_{x\rightarrow 0} \frac{f(x)-\sqrt{2}}{x}-5 =0.\end{equation}Quanto vale $f'(0)$?
Em primeiro lugar vamos tentar comparar a equação
\[\displaystyle\lim_{x\rightarrow 0} \frac{f(x) -\sqrt{2}}{x} -5=0\]com a expressão
$$\displaystyle\lim_{x\rightarrow x_0}\frac{erro(x)}{x-x_0}.$$Para isso, observe-se que
$$0=\lim_{x\rightarrow 0} \frac{f(x) -\sqrt{2}}{x} -5=\lim_{x\to 0}\frac{f(x)-f(0)-5(x-0)}{x-0}=\lim_{x\to 0} \frac{erro(x)}{x-0}$$Portanto, em vista da definição 1, a resposta é $f'(0) = 5$.
Dada $f: \mathbb R \rightarrow \mathbb R$, em que $f(-2) = -4$ e $f'(-2) = e$. Calcule $\displaystyle\lim_{h \rightarrow 0} \frac{f(-2+h) +4}{h}$
Olhando a definição 1 temos que
$$f(x)=f(x_0)+ f'(x_0)(x-x_0)+erro(x).$$Isolando a derivada obtemos
\[f'(x_0)= \frac{f(x)-f(x_0)}{x-x_0}+ \frac{erro(x)}{x-x_0}\]Tomando limite $x\to x_0$ em ambos lados da igualdade acima chegamos em
$$f'(x_0)=\lim_{x\to x_0} f'(x_0)=\lim_{x\to x_0} \left(\frac{f(x)-f(x_0)}{x-x_0}+ \frac{erro(x)}{x-x_0}\right)=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}+\lim_{x\to x_0} \frac{erro(x)}{x-x_0}=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}=\lim_{h\to 0} \frac{f(h+x_0)-f(x_0)}{h}$$Agora vamos sustituir na fórmula acima os elementos dados no problemas: $x_0=-2$, $f(x_0)=-4$, $f'(x_0)=e$ e
\begin{eqnarray}\tag{3} \lim_{h \rightarrow 0}\frac{f(-2+h) + 4}{h}h=f'(x_0)=\lim_{h \rightarrow 0}\frac{f(x_0+h)-f(x_0}{h}=e. \end{eqnarray}Suponha que $f$ e $g$ são duas funções reais, diferenciáveis em um intervalo $(a,b)$ tais que $g(x) = f(x) + k, \; \; \forall x \in (a,b)$, em que $k$ é uma constante real. Dado $x_0 \in (a,b)$ mostre que, $f'(x_0) = g'(x_0)$. Interprete geometricamente o resultado.
Usando o cômputo para a derivada obtido na equação ??? do exercicio anterior, temos
$$g'(x_0) = \displaystyle\lim_{x \to x_0} \frac{g(x) - g(x_0)}{x-x_0}= \displaystyle\lim_{x \to x_0} \frac{ (f(x) + k) - (f(x_0) + k)}{x-x_0}= \displaystyle\lim_{x \to x_0} \frac{f(x) - f(x_0)}{x-x_0}= f'(x_0).$$Como $f$ e $g$ diferem por uma constante, sabemos que seus gráficos são ``paralelos'', isto é, o gráfico de $g$ é o gráfico de $f$ deslocado ao longo do eixo $\hat{y}$ de $k$ unidades. O deslocamento não interfere na direç]ao da reta tangente em cada ponto e, portanto, a derivada é a mesma.
Em cada um dos itens seguintes são indicados os valores de $x_0$, $f(x_0)$, $f'(x_0)$, para alguma função $f: \mathbb R \rightarrow \mathbb R$. Obtenha a equa\ccao da reta tangente ao gráfico de $f$ em $(x_0, f(x_0))$.
$x_0 = 1$, $f(x_0) = 3$ e $f'(x_0) = -1$,
$x_0 = \pi$, $f(x_0) = 0$ e $f'(x_0) = 2$,
$x_0 = 0$, $f(x_0) = 5$ e $f'(x_0) = \sqrt{2}$.
Usando sempre a expressão $y = f(x_0) + f'(x_0)(x-x_0)$ temos
$y = 3 -(x-1)$
$y = 2(x-\pi)$
$y = 5 + \sqrt{2}x$.
A Figura a seguir contém o gráfico de duas funções, onde um gráfico é translação vertical do outro. Qual a diferença no valor de suas derivadas em cada ponto? (Observação: tente pensar apenas usando a informação de que a derivada mede a inclinação da reta tangente ao gráfico).
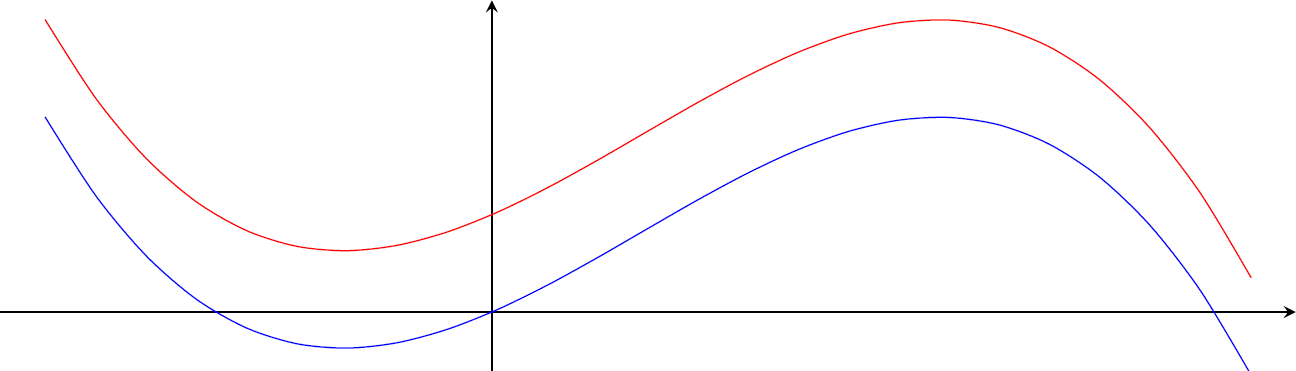
Não há diferença. As funções são uma translação vertical uma da outra. (Veja o exercício 5) A derivada mede o coeficiente angular da reta tangente ao gráfico. No caso, em cada ponto $x$, a reta tangente tem o mesmo coeficiente angular.
Cada uma das figuras a seguir é o esboço do gráfico de uma função. Identifique o sinal da derivada em cada ponto. (Observação: tente pensar geometricamente aqui).
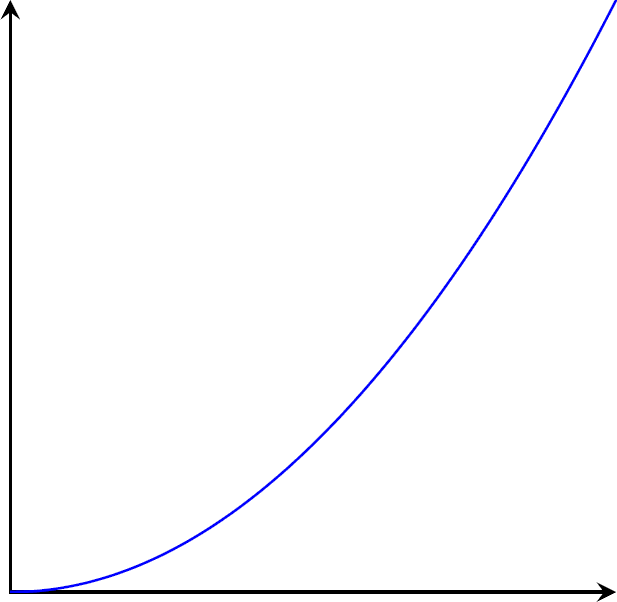 Figura 1
Figura 1
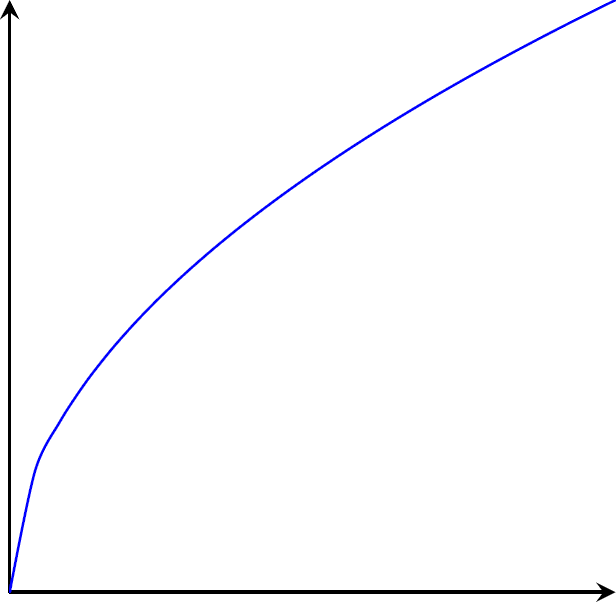 Figura 2
Figura 2
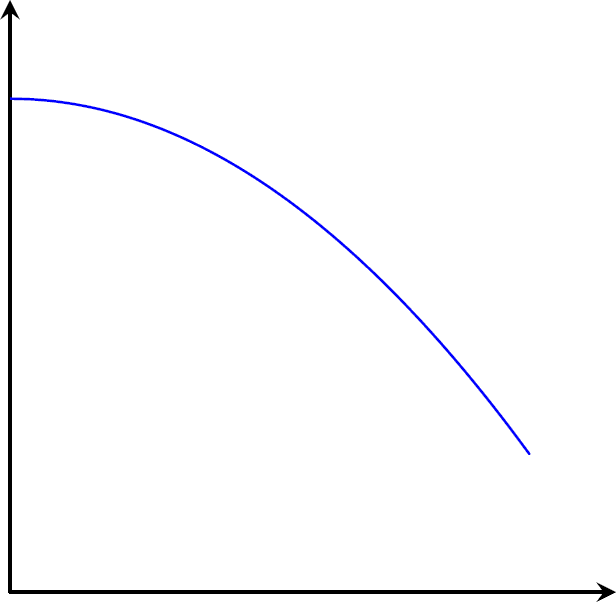 Figura 3
Figura 3
 Figura 4
Figura 4
As figuras 1 e 2 têm derivada positiva. Porem as figuras 3 e 4, a derivada é negativa.
Na figura a seguir, verifique que $f'(x_i)=0$, $i=1, 2, 3, 4$. Identifique os intervalos em que a derivada é positiva. Identifique os intervalos em que a derivada é negativa. Pense geometricamente.
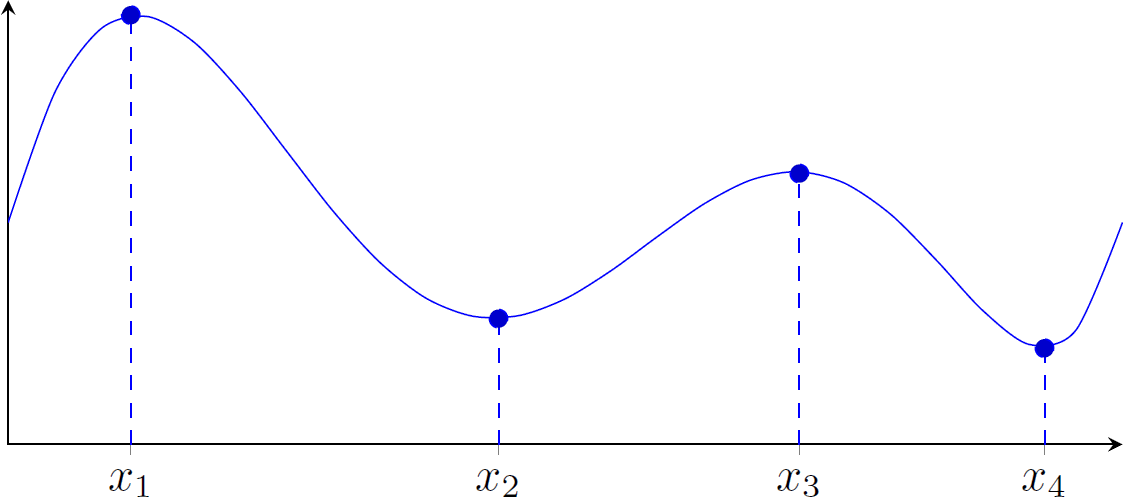
Para ver que a derivada vale $0$ em $x_i$, basta verificar que nesses pontos a tangente é paralela ao eixo $\hat{x}$. Observando a direção da tangente, concluímos que a derivada é negativa em $(x_1,x_2) \cup (x_3,x_4)$. É positiva em $(0,x_1) \cup (x_2,x_3) \cup (x_4,\infty)$.
Considere as funções $f$ e $g$ com domínio e contradomínio em $\mathbb R$. Ambas são diferenciáveis em todo o domínio. Os gráficos de $f$ e $g$ se intersectam perpendicularmente no ponto $(-1,3)$. A reta tangente ao gráfico de $f$ nesse ponto tem equação:
$$y = 3 +\displaystyle\frac{1}{2}(x+1).$$Quanto vale $g'(-1)$?
Pela equação da reta tangente ao gráfico de $g$, sabemos que o coeficiente angular dessa reta é $1/2$. A reta tangente ao gráfico de $g$, nesse ponto, tem que ser perpendicular a essa reta (por hipótese) e, portanto, tem coeficiente angular $-2$. Logo, $g'(-1) = -2$.
Use alguma das definições equivalentes de derivada para calcular $f'(x_0)$ e determine a equação da reta tangente ao gráfico da função no ponto $(x_0,f(x_0))$.
$f(x) = \dfrac{1}{x},\; x \neq 0, \; \;x_0=2$,
$f(x) = \dfrac{1}{x^2},\; x \neq 0, \; \; x_0=-1$.
Aplicando o cômputo da derivada obtido em (3), temos
$$f'(2)=\lim_{x \to 2} \frac{f(x)-f(2)}{x-2}=\lim_{x \to 2} \frac{\frac{1}{x}-\frac{1}{2}}{x-2}= \lim_{x \to 2} \frac{\frac{2-x}{2x}}{x-2}=-\lim_{x \to 2}\frac{1}{2x}= -\frac{1}{4}.$$Assim, a reta tangente ao gráfico de $f$ no ponto $(2,f(2))$ é
$$y=f(2)+f'(2)(x-2)= \frac{1}{2} -\frac{1}{4}(x-2)= -\frac{1}{4}x + 1.$$
Aplicando o cômputo da derivada obtido em (3), temos
$$f'(-1)=\lim_{x \to -1} \frac{f(x)-f(-1)}{x-(-1)}=\lim_{x \to -1} \frac{\frac{1}{x^2}-1}{x+1}= \lim_{x \to -1} \frac{\frac{1-x^2}{x^2}}{x+1}=\lim_{x \to -1}\frac{(1-x)}{x^2}= 2.$$Assim, a reta tangente ao gráfico de $f$ no ponto $(-1,f(-1))$ é
$$y=f(-1)+f'(-1)(x-(-1))= 1 + \left(2 \right)(x+1)= 2x +3.$$
Verifique se a função $f(x)$ é derivável em $x=1$ e se é contínua em $x=1$.
$f(x)= \begin{cases} \dfrac{3-x}{2}, &\text{se}\ x<1,\\ \dfrac{1}{\sqrt{x}}, &\text{se}\ x \geq 1. \end{cases} $
$f(x)= \begin{cases} -x,\ &\text{se}\ x<1,\\ \dfrac{1}{\sqrt{x}}, &\text{se}\ x \geq 1. \end{cases} $
Para saber se $f'(1)$ existe, calculamos os limites laterais
$$\lim_{x \to 1^-} \frac{f(x)-f(1)}{x-1}= \lim_{x \to 1^-} \frac{\frac{3-x}{2} - 1}{x-1}=\lim_{x \to 1^-}\frac{(3-x)-2}{2(x-1)}= \lim_{x \to 1^-} \frac{1-x}{2(x-1)}=\lim_{x \to 1^-} \left(- \frac{1}{2}\right) = - \frac{1}{2},$$$$\lim_{x \to 1^+} \frac{f(x)-f(1)}{x-1}= \lim_{x \to 1^+} \frac{\frac{1}{\sqrt{x}} - 1}{x-1}=\lim_{x \to 1^+}\frac{1-\sqrt{x}}{\sqrt{x}(x-1)} =\lim_{x \to 1^+} \left(- \frac{1}{\sqrt{x}(\sqrt{x}+1)}\right) = - \frac{1}{2}.$$
Assim o limite existe e
$$\displaystyle f'(1)=\lim_{x \to 1} \dfrac{f(x)-f(1)}{x-1}=-\frac{1}{2}.$$Isto é, $f$ é derivável em $x=1$, e como sabemos que se a função tem derivada em um ponto, ela é contínua nesse ponto, logo, $f$ é contínua em $x=1$.
Vejamos se $f$ é contínua em $x=1$, para isso devemos calcular os limites laterais
$$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (-x) = -1 \quad \text{e} \quad \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} \frac{1}{\sqrt{x}} = 1.$$Logo concluímos que $f$ não é contínua em $x=1$, e como sabemos que se a função tem derivada em um ponto, ela é contínua nesse ponto, $f$ também não será derivável em $x=1$.
Seja $f$ a função:
$$f(x)=\begin{cases} x\ \text{sen} \left(\dfrac{1}{x} \right), &\text{se}\ x \neq 0,\\1, &\text{se}\ x = 0. \end{cases} $$
$f$ é derivável em $x=0$? $f$ é contínua em $x=0$?
O que acontece se $f(0)=0$? $f$ é derivável em $x=0$? $f$ é contínua em $x=0$?
Pelo Teorema do Confronto temos que
$$\lim_{x \to 0} f(x) = \lim_{x \to 0} x\ \text{sen} \left(\dfrac{1}{x}\right) = 0 \neq 1 = f(0),$$então $f$ não é contínua em $x=0$, e como sabemos que se a função tem derivada em um ponto, ela é contínua nesse ponto, temos que $f$ não é derivável em $x=0$.
Como agora
$$f(x)= \begin{cases} x\ \text{sen} \left(\dfrac{1}{x}\right), &x \neq 0,\\ 0, &x = 0. \end{cases} $$Temos que
$\displaystyle f'(0)= \lim_{h \to 0} \frac{f(0+h)-f(0)}{h} = \lim_{h \to 0} \frac{f(h)-f(0)}{h} = \lim_{h \to 0} \frac{h\ \mathrm{sen} \left(\dfrac{1}{h}\right) - 0}{h} = \lim_{h \to 0} \mathrm{sen} \left(\frac{1}{h} \right).$ (Não existe)
Assim $f$ não é derivável em $x=0$. Mas, sabemos que $\displaystyle \lim_{x \to 0} f(x) = \lim_{x \to 0} x\ \text{sen} \left(\dfrac{1}{x}\right) = 0 = f(0)$, isto é, $f$ é contínua em $x=0$.
Seja $f$ a função:
$$f(x)=\begin{cases} x^2 \text{sen} \left(\dfrac{1}{x} \right), &\text{se}\ x \neq 0,\\1, &\text{se}\ x = 0. \end{cases} $$
$f$ é derivável em $x=0$? $f$ é contínua em $x=0$?
E se tivermos $f(0)=0$? $f$ é derivável em $x=0$? $f$ é contínua em $x=0$?
Pelo Teorema do Confronto temos que
$$\lim_{x \to 0} f(x) = \lim_{x \to 0} x^2 \text{sen} \left(\dfrac{1}{x}\right) = 0 \neq 1 = f(0),$$então $f$ não é contínua em $x=0$, e como sabemos que se a função tem derivada em um ponto, ela \'e cont\'inua nesse ponto, temos que $f$ não é derivável em $x=0$.
Como agora
$$f(x)= \begin{cases} x^2 \text{sen} \left(\dfrac{1}{x}\right), &x \neq 0,\\ 0, &x = 0. \end{cases} $$Pelo item 1 sabemos que agora $f(x)$ é contínua no ponto $x=0$, pois temos que
$$\lim_{x \to 0} f(x) = \lim_{x \to 0} x^2 \text{sen} \left(\dfrac{1}{x}\right) = 0 = f(0).$$Então não podemos aplicar o raciocínio do item 1 para concluir a solução. O que devemos fazer agora é aplicar diretamente a definição, isto é
$$f'(0)= \lim_{h \to 0} \frac{f(0+h)-f(0)}{h} = \lim_{h \to 0} \frac{f(h)-f(0)}{h} = \lim_{h \to 0} \frac{h^2 \text{sen} \left( \dfrac{1}{h} \right) - 0}{h} = \lim_{h \to 0} h\ \text{sen} \left(\frac{1}{h}\right) = 0.$$Assim $f$ é derivável em $x=0$.
Esboce um gráfico de alguma função $f(x)$ com domínio e contradomínio em $\mathbb R$ com todas as seguintes propriedades.
$f$ é descontínua em exatamente dois pontos.
$\displaystyle\lim_{x\rightarrow \infty} f(x) = 1$.
A derivada de $f$ não existe em exatamente $4$ pontos.
A derivada de $f$ é positiva se $x \in (0,2)$ e negativa se $x\in (-2, 0)$.
Esboce um gráfico de alguma função $f(x)$ com domínio e contradomínio em $\mathbb R$ com todas as seguintes propriedades.
$f$ tem uma assíntota vertical.
$f$ é diferenciável em todos os seus pontos de continuidade.
A derivada de $f$ é sempre positiva.
Esboce um gráfico de alguma função $f(x)$ com domínio e contradomínio em $\mathbb R$ com todas as seguintes propriedades.
$f$ é diferenciável em $\mathbb R$.
$f$ é crescente.
A derivada de $f$ é decrescente.
$f$ tem pelo menos uma assíntota horizontal.
Esboce um gráfico de alguma função $f(x)$ com domínio e contradomínio em $\mathbb R$ com todas as seguintes propriedades.
$f$ não é diferenciável se $x$ é um número natural.
$f$ é diferenciável se $x \in \mathbb R - \mathbb N$.
A derivada de $f$, nos intervalos em que existe é constante.
A derivada de $f$ assume valores positivos e negativos.
A derivada de $f$ vale $0$ em pelo menos um intervalo.