
Nos itens abaixo dê os intervalos em que a função é crescente e em que é decrescente.
$f(x)=x+\dfrac{3}{x^2}$
$g(t)=\dfrac{3t^2+4t}{1+t^2}$
$F(u)=\dfrac{u^2-u+1}{2(u-1)}$
Crescente nos intervalos $(-\infty, 0)$ e $\left(\sqrt[3]{6},\infty\right)$, decrescente em $\left(0,\sqrt[3]{6}\right)$.
Crescente em $\left(-\frac{1}{2},2\right)$, decrescente nos intervalos $\left(-\infty, -\frac{1}{2}\right)$ e $\left(2,\infty\right)$.
Crescente nos intervalos $(-\infty, 0)$ e $ \left(2,\infty\right)$, decrescente nos intervalos $(0,1)$ e $(1,2)$.
Seja $f$ uma função tal que $f(0)=0$ e $f'(x)=\dfrac{x^2}{1+x^2},\ \forall x \in\mathbb{R}$. Mostre que $0<f(x)<x , \forall x >0$.
Primeiro vamos mostrar que $f(x)>0, \ \forall x> 0$.
(i) $f'(x)=\dfrac{x^2}{1+x^2}>0, \ \forall x\neq 0 \Longrightarrow f$ é crescente em $(-\infty,0)\cup (0,\infty)$;
(ii) A função $f$ é contínua em $\mathbb{R}$ pois $f$ é diferenciável em $\mathbb{R}$.
Por (i) e (ii) concluímos: $f$ é crescente em $(0,\infty)$ e contínua em $[0,\infty) \Longrightarrow f(x)>f(0), \ \forall x> 0$.
Finalmente, como por hipótese $f(0)=0$, concluímos que $f(x)>0, \ \forall x>0$.
Agora vamos mostrar que $f(x)<x, \ \forall x> 0$. Mas $f(x)<x, \ \forall x>0 \Longleftrightarrow x-f(x)>0, \ \forall x>0$. Considerando $F(x)=x-f(x)$ temos que provar que $F(x)>0, \ \forall x>0$. Provando:
(i) $F'(x)=1-\dfrac{x^2}{1+x^2}=\dfrac{1}{1+x^2}>0,\ \ x\neq 0\Longrightarrow f$ é crescente em $(-\infty,0)\cup (0,\infty)$;
(ii) A função $F$ é contínua em $\mathbb{R}$ pois é a diferença de funções contínuas em $\mathbb{R}$.
Por (i) e (ii) concluímos: $F$ é crescente em $(0,\infty)$ e contínua em $[0,\infty) \Longrightarrow F(x)>F(0), \ \forall x> 0$.
Como $F(0)=0-f(0)=0$, concluímos que $F(x)>0, \ \forall x>0$.
Mostre que $\mathrm{sen} x <x, \ \ \forall x>0$.
(Sugestão: para $x\geq \pi/2$, use propriedades da trigonometria, para $0<x<\pi/2$, use derivada)
Para $x\geq \dfrac{\pi}{2}$. Como $1<\dfrac{\pi}{2}$ e $\mathrm{sen} x\leq 1$, temos que $\mathrm{sen} x \leq1<\dfrac{\pi}{2}\leq x$. Logo $\mathrm{sen} x < x$.
Para $0<x< \dfrac{\pi}{2}$. Como $\mathrm{sen} x<x \Longleftrightarrow x-\mathrm{sen}x>0$, considere $F(x)=x-\mathrm{sen} x$.
Como $F$ é a soma de funções contínuas em $\mathbb{R}$, concluímos que $F$ é contínua em $\mathbb{R}$. (*)
$F'(x)=1-\cos x$ e sabemos que $\cos x <1,\ \forall x\in\left(0,\dfrac{\pi}{2}\right)$. Logo $ F'(x)=1-\cos x >0 \ \forall x\in\left(0,\dfrac{\pi}{2}\right)$.
Assim concluímos que $F$ é crescente em $\left(0,\dfrac{\pi}{2}\right)$. (**)
Pelas conclusões (*) e (**), temos que $F(x)=x-\mathrm{sen} x>F(0)=0, \ \forall x\in\left(0,\dfrac{\pi}{2}\right)$.
Mostre que $f(x)=\dfrac{\mathrm{ln} x}{x}$ tem máximo absoluto em $x=e$. Conclua que $\pi^{e}< e^{\pi}$.
Domínio de $f=(0,\infty)$. Derivando, $f'(x)= \dfrac{1-\mathrm{ln}x}{x^2}$. Analisando o sinal de $f'(x)$, temos $f'(x)>0$ quando $0<x<e$; $f'(x)<0$ quando $x>e \Rightarrow f$ é crescente quando $0<x<e$; $f$ é decrescente quando $x>e$. Logo $f$ tem um máximo relativo no único ponto crítico $x=e$. Como $f$ é contínua em $x=e$, concluímos que $f$ tem um máximo absoluto em $x=e$.
Provando a desigualdade: $f$ tem máximo absoluto em $x=e \Rightarrow f(\pi)<f(e)=\dfrac{\mathrm{ln} e}{e}=\dfrac{1}{e}\Rightarrow$ $f(\pi)=\dfrac{\mathrm{ln} \pi}{\pi}<\dfrac{1}{e}$. Como $e>0$ e $\pi>0$, temos: $e \,\mathrm{ln} \pi <\pi $. Aplicando a propriedade de logaritmo de potência, temos $e \mathrm{ln} \pi=\mathrm{ln}{\pi ^e}$, logo $\mathrm{ln} \pi^e<\pi$. Sabemos que a função exponencial é estritamente crescente, logo $e^{\mathrm{ln} \pi^e}<e^{\pi}$. Sabemos que $e^{\mathrm{ln} x}=x, \forall x>0$, em particular $e^{\mathrm{ln} \pi^e}=\pi^e$. Logo, $\pi^e<e^{\pi}$.
Mostre que $p(x)=x^3-3x^2+6$ tem exatamente uma raiz real e localize-a em um intervalo de amplitude máxima 1.
Vamos primeiro estudar o crescimento de $p$. Como $p'(x)=3x^2-6x$ então:
| $-\infty \leftarrow x$ | $x<0$ | $x=0$ | $0<x<2$ | $x=2$ | $2<x$ | $x\rightarrow \infty$ | |
| $p'(x)$ | $+$ | $0$ | $-$ | $0$ | $+$ | ||
| $p(x)$ | $-\infty$ | cresce | $6$ | decresce | $2$ | cresce | $\infty$ |
Como $p$ é contínua, pelo Teorema do Valor Intermediário sabemos que no intervalo $(-\infty,0)$ o polinômio tem uma raiz. Vamos agora tentar diminuir esse intervalo para um de amplitude $1$. Como $p(-1)=2$ e $p(-2)=-14$, novamente pelo TVI concluimos que $p$ tem uma raiz no intervalo $(-2,-1)$ e como $f$ é crescente nesse intervalo, então essa raiz é única.
Mostre que $f(x)=x^2-x\mathrm{sen} x-\cos x$ tem exatamente duas raízes reais e localize-as em intervalos de amplitude máxima $\pi /2$.
Vamos primeiro estudar o crescimento de $f$. Como $f'(x)=2x-\mathrm{sen} x -x \cos x+\mathrm{sen} x=2x -x \cos x=x\left(2 - \cos x\right)$ e $\cos x \neq 2$ para todo $x \in \mathbb{R}$ então:
| $-\infty \leftarrow x$ | $x<0$ | $x=0$ | $0<x$ | $x\rightarrow +\infty$ | |
| $f'(x)$ | $-$ | $0$ | $+$ | ||
| $f(x)$ | $+\infty$ | decresce | $-1$ | cresce | $+\infty$ |
Como $f\left(\frac{\pi}{2}\right)=\frac{\pi^2-2\pi}{4}>0$ e $f\left(-\frac{\pi}{2}\right)=\frac{\pi^2+2\pi}{4}>0$ e $f$ é contínua, pelo Teorema do Valor Intermediário sabemos que nos intervalos $\left(-\frac{\pi}{2},0\right)$ e $\left(0,\frac{\pi}{2}\right)$ a função admite pelo menos uma raiz, mas como $f$ é monótona em cada um desses intervalos, concluímos que tem exatamente uma rais em cada um deles.
Prove que para todo $x> 0$ vale a seguinte desigualdade: $x+\dfrac{1}{x}\geq 2$.
(Sugestão: estude o crescimento da expressão do lado esquerdo e determine o mínimo absoluto dessa expressão no intervalo dado).
Seja $f(x)=x+\dfrac{1}{x}$. Vamos estudar o crescimento de $f$. Como $f'(x)=1-\dfrac{1}{x^2}$ então:
| $-\infty \leftarrow x$ | $x<-1$ | $x=-1$ | $-1<x<0$ | $x=0$ | $0<x<1$ | $x=1$ | $1<x$ | $x\rightarrow +\infty$ | |
| $f'(x)$ | $+$ | $0$ | $-$ | $\nexists$ | $-$ | $0$ | $+$ | ||
| $f(x)$ | $-\infty$ | cresce | $-2$ | decresce | $\nexists$ | decresce | $2$ | cresce | $+\infty$ |
No intervalo $(0,\infty)$, o mínimo absoluto de $f(x)=x+\dfrac{1}{x}$ é igual a $f(1)=2$. Logo $f(x)\geq f(1)=2$.
A concentração $C$ de certa substância química no fluxo sanguíneo em $t$ horas após ter sido injetada no músculo é dada por $C(t)=\dfrac{3t}{54+t^3}, t\geq 0$. Em que instante a concentração é máxima? Qual é a concentração máxima?
Derivando, $C'(t)= \dfrac{3(54+t^3)-3t.3t^2}{(54+t^3)^2}=\dfrac{6(27-t^3)}{(54+t^3)^2}$. Analisando o sinal de $C'(t)$, temos, $C'(t)=0$, quando $t=3$; $C'(t)>0$ quando $0<t<3$; $C'(t)<0$ quando $t>3 \Rightarrow C(t)$ é crescente quando $0<t<3$; $C(t)$ é decrescente quando $t>3$. Logo $C(t)$ tem um máximo relativo no único ponto crítico $t=3$. Como $C(t)$ é contínua em $t=3$, concluímos que $C(t)$ tem um máximo absoluto em $t=3$ horas. No instante $t=3$ horas, a concentração é máxima e igual a $\dfrac{1}{9}=0,1111...=0,\overline{\,1}$.
Nos itens abaixo esboce o gráfico da função $f$ e dê explicitamente o que se pede:
domínio $\mathrm{D}$ de $f$;
paridade de $f$;
equações das assíntotas verticais e horizontais do gráfico;
intervalos de $\mathrm{D}$ em que $f$ é contínua;
pontos de $\mathrm{D}$ em que a tangente ao gráfico é vertical;
intervalos de $\mathrm{D}$ onde $f$ é crescente e onde $f$ é decrescente;
extremos relativos de $f$ e os respectivos pontos de $\mathrm{D}$ onde ocorrem;
intervalos onde a concavidade do gráfico é para cima, onde é para baixo e os seus pontos de inflexão;
extremos absolutos de $f$ e os respectivos pontos de $\mathrm{D}$ onde ocorrem;
imagem de $f$.
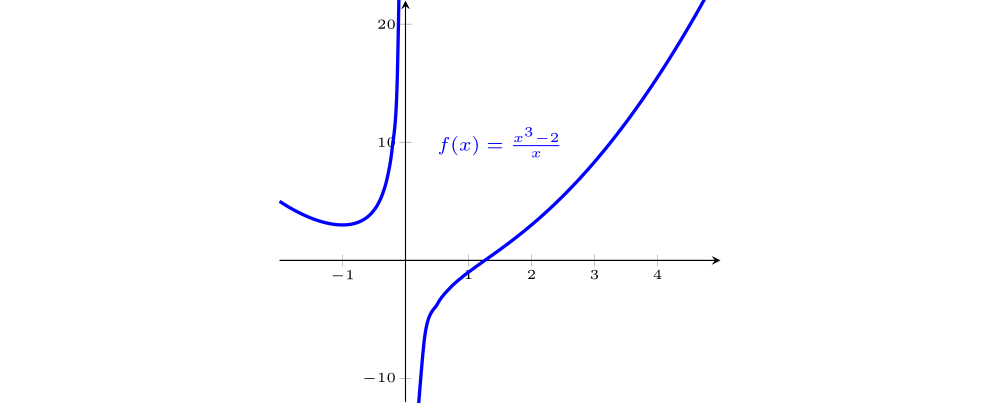
$f(x)=\dfrac{x^3-2}{x}$
$f(x)=(x-1)x^{2/3}$
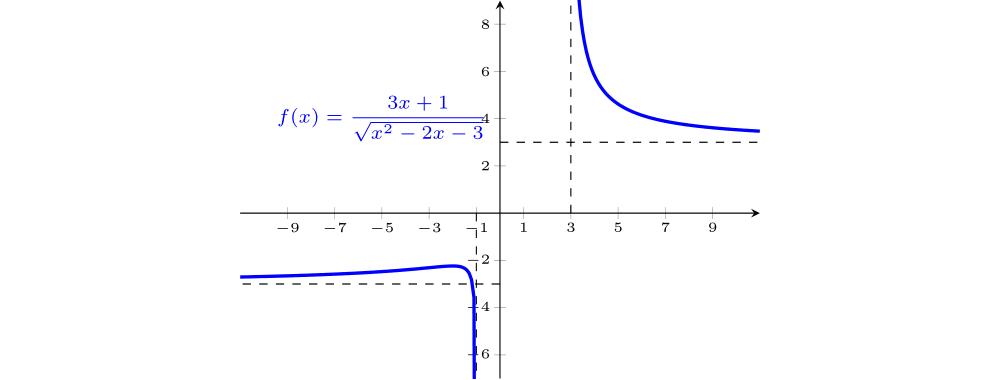
$f(x)= \dfrac{3x+1}{\sqrt{x^2-2x-3}}$
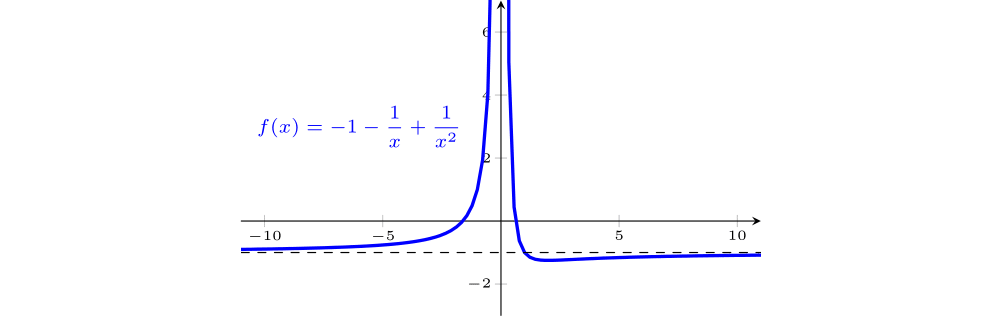
$f(x)=-1-\dfrac{1}{x}+\dfrac{1}{x^2}$
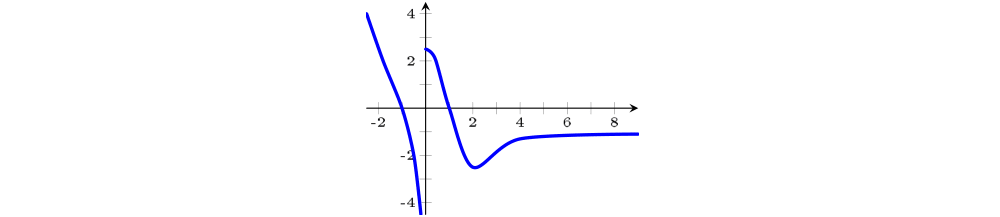
$f(x)=x-5\arctan x$
$\mathrm{D}=(-\infty,0)\cup (0,\infty)$; nem par, nem ímpar; contínua em $\mathrm{D}$; assíntota vertical: $x=0$, não tem assíntota horizontal; não tem reta tangente vertical; crescente nos intervalos $(-1,0)$ e $(0,\infty)$, decrescente em $(-\infty,-1)$; mínimo relativo $=f(-1)=3$, não tem máximo relativo; concavidade para cima em $(-\infty,0)\cup \left(\sqrt[3]{2},\infty \right)$, para baixo em $\left(0,\sqrt[3]{2}\right)$, ponto de inflexão $=\left(\sqrt[3]{2},f\left(\sqrt[3]{2}\right)\right)=\left(\sqrt[3]{2},0\right)$; não tem mínimo absoluto pois $\displaystyle \lim_{x\rightarrow 0^+}f(x)=-\infty$, não tem máximo absoluto pois $\displaystyle \lim_{x\rightarrow 0^-}f(x)=\infty$; imagem $=(-\infty,\infty)$.
$\mathrm{D}=(-\infty,\infty)$; nem par, nem ímpar; contínua em $\mathrm{D}$; não tem assíntota vertical, não tem assíntota horizontal; reta tangente vertical: $x=0$; crescente nos intervalos $(-\infty,0)$ e $(2/5,\infty)$; decrescente em $(0,2/5)$; mínimo relativo $=f(2/5)=\left(-3\sqrt[3]{20}\right)/25$, máximo relativo $=f(0)=0$; concavidade para cima em $(-1/5,0)\cup (0,\infty)$, para baixo em $(-\infty,-1/5)$, ponto de inflexão $=\left(-1/5,-6\sqrt[3]{5}/25\right)$; não tem mínimo absoluto pois $\displaystyle \lim_{x\rightarrow -\infty}f(x)=-\infty$, não tem máximo absoluto pois $\displaystyle \lim_{x\rightarrow \infty}f(x)=\infty$;imagem $=(-\infty,\infty)$.

$\mathrm{D}=(-\infty,-1)\cup (3,\infty)$; nem par, nem ímpar; contínua em $\mathrm{D}$; assíntotas verticais: $x=-1$ e $x=3$, assíntotas horizontais: $y=-3$ e $y=3$; não tem reta tangente vertical; crescente em $(-\infty,-2)$; decrescente nos intervalos $(-2,-1)$ e $(3,\infty)$; não tem mínimo relativo, máximo relativo $=f(-2)=-\sqrt 5$; concavidade para cima em $(-\infty ,-3)\cup (3,\infty)$, para baixo em $(-3,-1)$, ponto de inflexão $=\left(-3,-4\sqrt{3}/3\right)$; não tem mínimo absoluto pois $\displaystyle \lim_{x\rightarrow -1 ^{-}}f(x)=-\infty$, não tem máximo absoluto pois $\displaystyle \lim_{x\rightarrow 3^{+}}f(x)=\infty$ ; imagem $=\left(-\infty,-\sqrt 5\right]\cup (3,\infty)$.
$\mathrm{D}=(-\infty,0)\cup (0,\infty)$; nem par, nem ímpar; contínua em $\mathrm{D}$; assíntota vertical: $x=0$, assíntota horizontal: $y=-1$; não tem reta tangente vertical; crescente nos intervalos $(-\infty,0)$ e $(2,\infty)$; decrescente em $(0,2)$; mínimo relativo $=f(2)=-5/4$, não tem máximo relativo; concavidade para cima em $(-\infty,0)\cup (0,3)$, para baixo em $(3,\infty)$, ponto de inflexão $=(3,-11/9)$; mínimo absoluto $=f(2)=-5/4$, não tem máximo absoluto pois $\displaystyle \lim_{x\rightarrow 0}f(x)=\infty$; imagem $= [-5/4,\infty)$.
$\mathrm{D}=(-\infty,\infty)$; é ímpar; contínua em $\mathrm{D}$; não tem assíntota vertical, não tem assíntota horizontal; não tem reta tangente vertical; crescente nos intervalos $(-\infty,-2)$ e $(2,\infty)$, decrescente em $(-2,2)$; mínimo relativo $=f(2)=2-5\arctan 2\cong -3,55$, máximo relativo $=f(2)=-2+ 5\arctan 2\cong 3,55$; concavidade para cima em $(0,\infty)$, para baixo em $(-\infty,0)$, ponto de inflexão $=(0,0)$; não tem mínimo absoluto pois $\displaystyle \lim_{x\rightarrow -\infty}f(x)=-\infty$, não tem máximo absoluto pois $\displaystyle \lim_{x\rightarrow \infty}f(x)=\infty$; imagem $= (-\infty,\infty)$.

Seja $f: \mathbb{R}^* \longrightarrow \mathbb{R}$ duas vezes diferenciável e tal que
$f(x)\neq 0,\ \ \forall x\in \mathbb{R}^*$, $f(-1)= -2$ e $f(1)=3$;
$\displaystyle \lim _{x\rightarrow 0^-}f(x)=-\infty$, $\displaystyle \lim _{x\rightarrow 0^+}f(x)=0$, $\displaystyle \lim _{x\rightarrow-\infty}f(x)=-\infty$, $\displaystyle \lim _{x\rightarrow \infty}f(x)=0$,
$f''(x)<0$ se {$x\neq0$ e $x<2$}, $f''(x)=0$ se $x=2$, $f''(x)>0$ se $x>2$;
o gráfico de $f'$ está dado ao lado.
Nestas condições,
prove que $f(x)>0,\ \forall x>0$
prove que $f(x)<0,\ \forall x<0$
esboce um possível gráfico de $f$.
Primeiro observe que por hipótese, $\exists f''(x), \forall x\neq 0 \Longrightarrow \exists f'(x), \forall x\neq 0 \Longrightarrow f$ é contínua $\forall x\neq 0$.
O gráfico de $y=f'(x)$ e os outros dados conduzem ao seguinte quadro: \scriptsize
| $-\infty \leftarrow x $ | $x<-1$ | $x=-1$ | $-1<x<0$ | $x\rightarrow 0^-$ | $0 ^+\leftarrow x$ | $0<x<1$ | $x=1$ | $1<x$ | $x\rightarrow \infty$ | |
| $f'(x)$ | $+$ | $0$ | $-$ | $-$ | $+$ | $+$ | $0$ | $-$ | ||
| $f(x)$ | $-\infty $ | cresce | $-2$ | decresce | $ -\infty$ | $0$ | cresce | $3$ | decresce | $0$ |
Como $\displaystyle \lim_{x\rightarrow 0^+}f(x)=0$ , $f$ é crescente no intervalo $(0,1)$, é contínua no intervalo $(0,1]$, $f(1)=3>0$, podemos concluir que $f(x)>0$ no intervalo $(0,1]$.
Como $f(1)=3>0$, $f$ é contínua no intervalo $[1,\infty)$, decrescente no intervalo $(1,\infty)$, $\displaystyle \lim_{x\rightarrow \infty}f(x)=0$, podemos concluir que $f(x)>0$ no intervalo $[1,\infty)$.
Como $\displaystyle \lim_{x\rightarrow -\infty}f(x)=-\infty$, $f$ é crescente no intervalo $(-\infty,-1)$, é contínua no intervalo $(-\infty,-1]$, $f(-1)=-2<0$, podemos concluir que $f(x)<0$ no intervalo $(-\infty,-1]$.
Como $f(-1)=-2<0, \displaystyle \lim_{x\rightarrow0^{-}}f(x)=0$, $f$ é contínua no intervalo $[-1,0)$, decrescente no intervalo $(-1,0)$, $\displaystyle \lim_{x\rightarrow 0^{-}}f(x)=0$, podemos concluir que $f(x)<0$ no intervalo $[-1,0)$.
Como $f'(1)=0$, $f$ é contínua no intervalo $(0,\infty)$, $f$ é crescente no intervalo $(0,1)$, $f$ é decrescente no intervalo $(1,\infty)$, podemos concluir que $f$ tem um máximo relativo em $x=1$, onde o gráfico de $f$ tem reta tangente horizontal.
Como $f'(-1)=0$, $f$ é contínua no intervalo $(-\infty,0)$, $f$ é crescente no intervalo $(-\infty,-1)$, $f$ é decrescente no intervalo $(-1,0)$, podemos concluir que $f$ tem um máximo relativo em $x=-1$, onde o gráfico de $f$ tem reta tangente horizontal.
Analisando a concavidade do gráfico:
$f''(x)<0$ se $x<0$ ou $0<x<2\Longrightarrow$ o gráfico é côncavo para baixo nos intervalos $(-\infty,0)$ e $(0,2)$.
$f''(x)>0$ se $x>2 \Longrightarrow$ o gráfico é côncavo para cima no intervalo $(2,\infty)$.
Esboce os gráficos das funções abaixo.
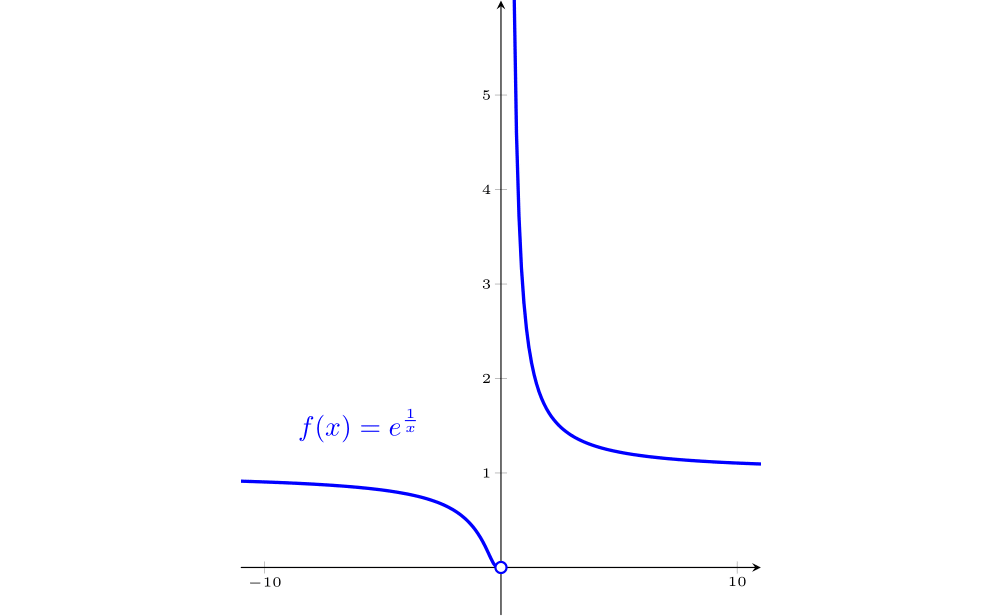
$f(x)=e^{\frac{1}{x}}$
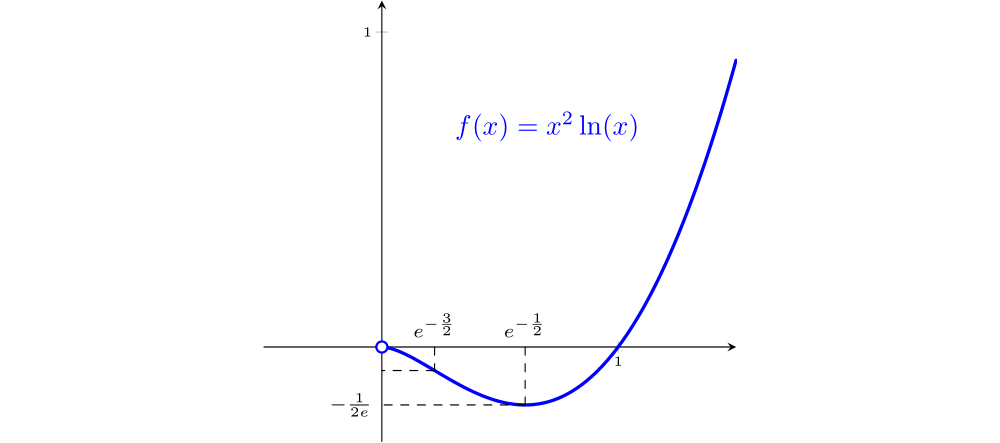
$f(x)=x^2\mathrm{ln} x$
$f(x)=xe^{-x}$
$\mathrm{D}(f)=\mathbb{R}-\{0\}$
$\displaystyle\lim_{x\rightarrow -\infty} f(x)=1$, $\displaystyle\lim_{x\rightarrow \infty} f(x)=1$
$\displaystyle\lim_{x\rightarrow 0^-} f(x)=0$, $\displaystyle\lim_{x\rightarrow 0^+} f(x)=\infty$
Assíntota horizontal $y= 1$, Assíntota vertical $x=0$
$$f'(x)=\frac{-e^{1/x}}{x^2}$$Então $f'(x)<0$ em $\mathbb{R}-{0}$. Logo $f(x)$ é decrescente em $\mathbb{R}-\{0\}$ e não tem pontos críticos.
$$f''(x)=e^{1/x}\frac{1+2x}{x^4}$$Então $f''(x)=0 \Leftrightarrow 1+2x=0$ ou $x=-1/2$. Temos um ponto de inflexão em $x=-1/2$, concavidade para baixo em $(\infty, -2)$, concavidade para cima em $(-2,0)\cup (0,\infty)$.
$\mathrm{D}(f)=(0, +\infty)$
$\displaystyle\lim_{x\rightarrow 0^+} f(x)=0$, $\displaystyle\lim_{x\rightarrow \infty} f(x)=\infty$
$$f'(x)=x(2\mathrm{ln}(x)+1)$$Logo $f'(x)=0\Leftrightarrow 2\mathrm{ln}(x)+1=0$ e temos um ponto crítico em $x=e^{-1/2}$. Então $f$ é decresente em $(0, e^{-1/2}]$, crescente em $[e^{-1/2}, \infty)$, e tem um mínimo absoluto em $f\left(e^{-1/2}\right)=-\dfrac{1}{2e}.$
$$f''(x)=2\mathrm{ln}(x)+3$$Ponto de inflexão $x=e^{-3/2}$, concavidade para baixo em $(0, e^{-3/2})$, concavidade para cima em $(e^{-3/2}, \infty)$.
$\mathrm{D}(f)=\mathbb{R}$
$\displaystyle\lim_{x\rightarrow -\infty} f(x)=-\infty$, $\displaystyle\lim_{x\rightarrow \infty} f(x)=0$
Assíntota horizontal: $y=0$
$$f'(x)=e^{-x}(1-x)$$Ponto crítico em $x=1$, $f$ é crescente em $(-\infty, 1]$, decrescente em $[1, \infty)$ com um máximo absoluto $f(1)=\dfrac{1}{\ e \ }$.
$$f''(x)=-e^{-x}(2-x).$$Ponto de inflexão em $x=2$, concavidade para baixo no intervalo $(-\infty, 2)$, concavidade para cima em $(2,\infty)$.
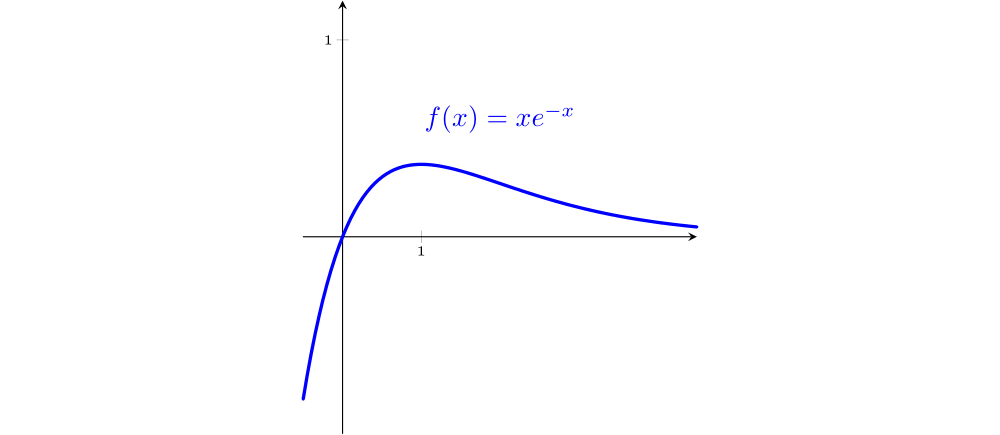
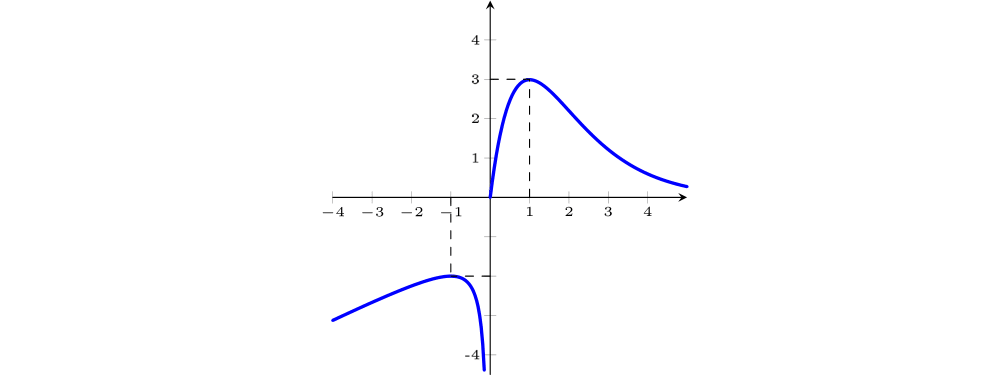
Sejam $f$ e $g$ funções com domínio $\mathbb{R}$ e cujos gráficos estão representados abaixo.
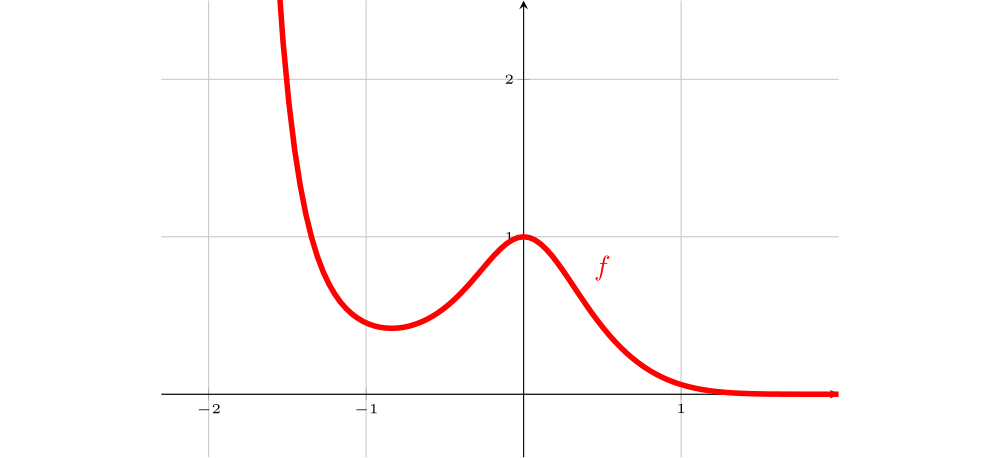
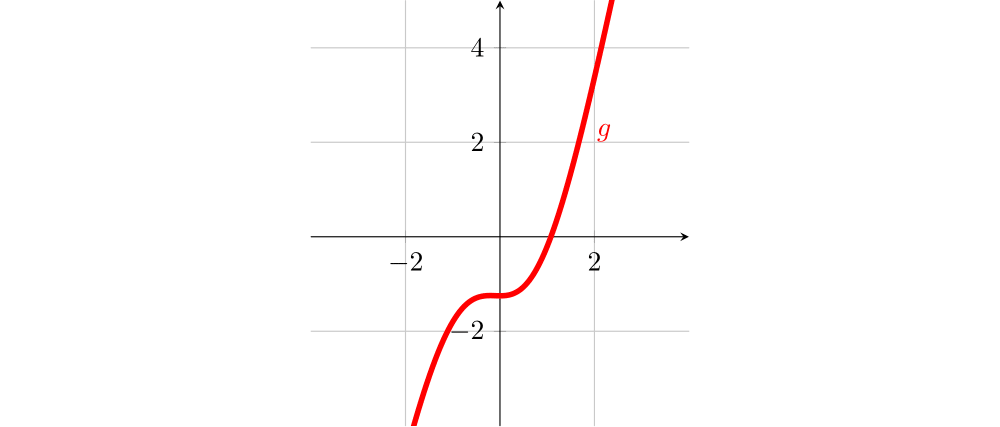
Dos gráficos abaixo, indique os que representam as funções derivadas $f'$, $f''$, $g'$ e $g''$.
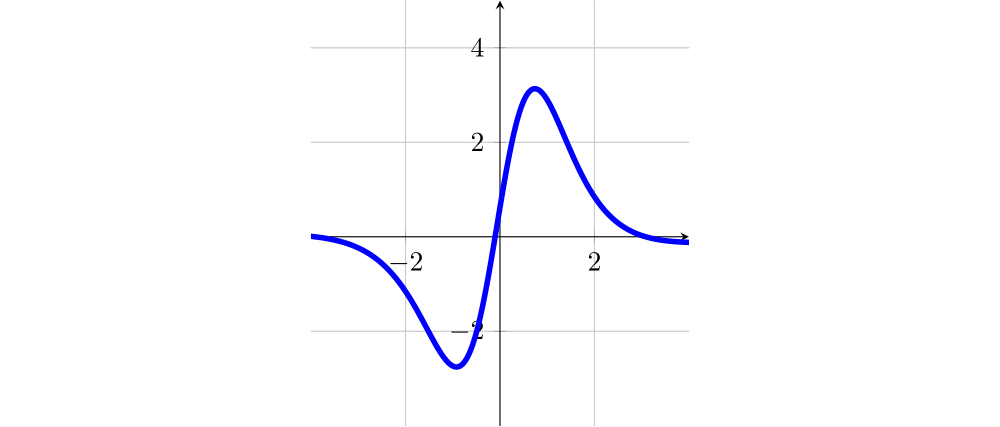
Gráfico 1
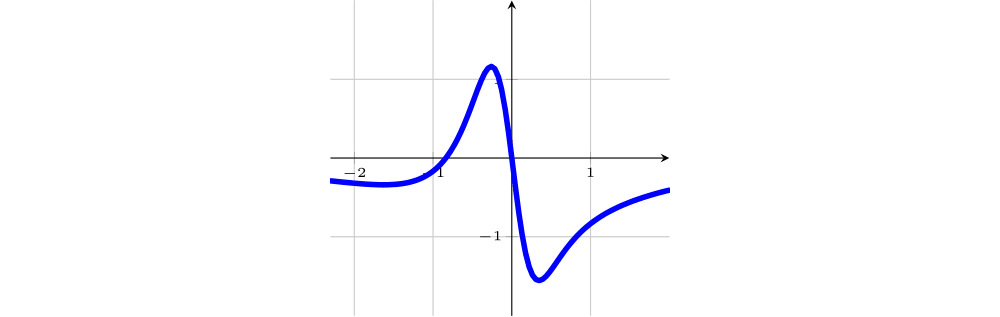
Gráfico 2
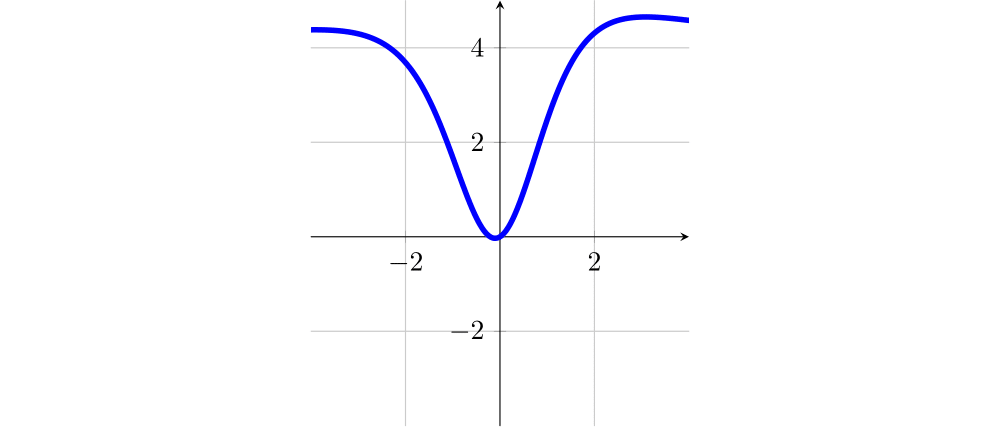
Gráfico 3
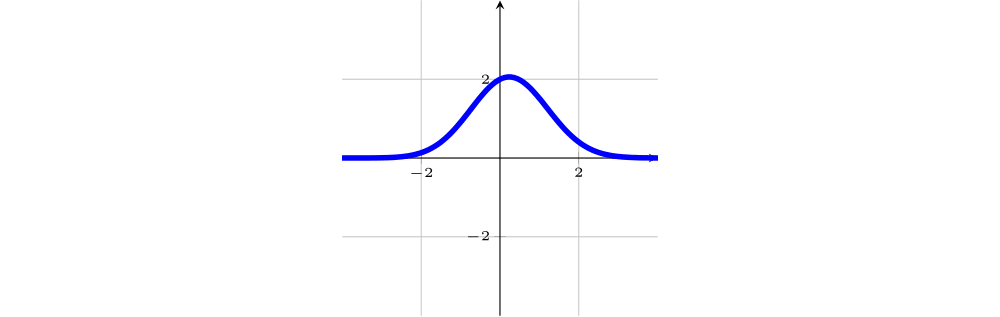
Gráfico 4
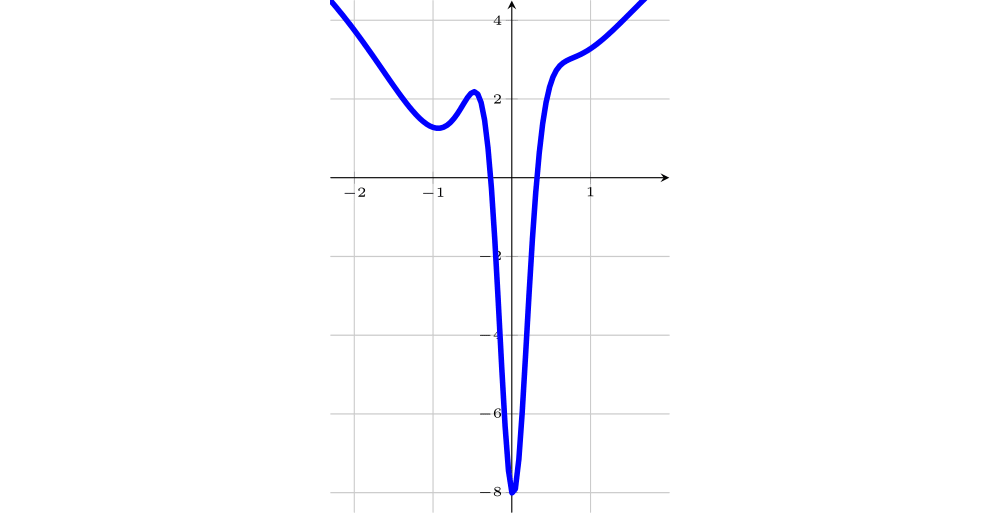
Gráfico 5

Gráfico 6
Analisando o gráfico da função $f$:
Extremos locais: Existe um mínimo local $x_1 \in (-1,-0,5)$, onde $f'(x_1)=0$. Também existe um máximo local $x_2\approx 0$, onde $f'(x_2)=0$. Sinal da derivada: $f'(x)<0$ se $x<x_1$, $f'(x_1)=0$, $f'(x)>0$, se $x_1<x<x_2$, $f'(x_2)=0$ e $f'(x)<0$, se $x>x_2$.
Portanto, o gráfico da $f'$ é o 2, pois é o único com as características acima.
O gráfico da $f$ tem concavidade para cima quando $x<x_3 $, onde $x_3$ é um ponto de mudança de concavidade(onde $f'$ tem um máximo local-Gráf2) e nesse caso $f''(x_3)=0$, $f''(x)>0,$ para $x<x_3$. Note que $x_3$ é negativo e está entre $-0,5 $ e $0$. O gráfico da $f$ tem concavidade para baixo quando $x_3<x<x_4 $, onde $x_4$ é um ponto de mudança de concavidade ou seja, de inflexão (onde $f'$ tem um mínimo local-Gráf2) e nesse caso $f''(x_4)=0$, $f''(x)<0,$ para $x_3<x<x_4$. Note que $x_3$ é negativo e está entre $-0,5 $ e $0$.Note que $x_4$ é positivo e está entre $0 $ e $1$.
Portanto, o gráfico da $f''$ é o 5, pois é o único com as características acima.
Analisando o gráfico da função $g$:
Extremos locais: Não há.
Sinal da derivada: $g'(0)=0$ e $g'(x)>0$ se $x\neq 0$. Note que as inclinações das tangentes ao gráfico da $g$ são positivas para $x<0$, decrescem a zero e voltam a ficar positivas para $x>0$. Portanto, o gráfico da $g'$ é o 3, pois é o único com as características acima.
O gráfico da $g$ tem concavidade para baixo quando $x<0 $, onde $x=0$ é um ponto de mudança de concavidade, ou seja, de inflexão (onde $g'$ tem um mínimo local-Gráf3) e nesse caso $g''(0)=0$, $g''(x)<0,$ para $x<0$ e $g''(x)>0$, para $x>0$. Portanto, o gráfico da $g''$ é o 1, pois é o único com as características acima.