
Determine o(s) ponto(s) da curva $y=x^2+1$ mais próximo(s) do ponto $(0,2)$.
Consiferemos a figura abaixo que esquematiza o nosso problema.
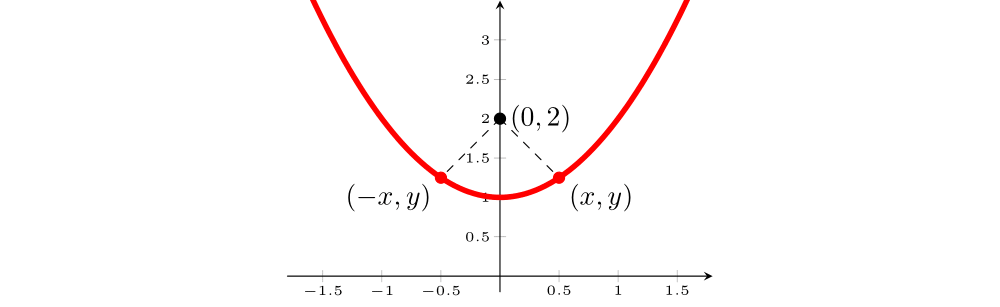
A distância entre um ponto $(x,y)$ qualquer e o ponto $(0,2)$ é dada por $d((x,y),(0,2))=\sqrt{x^2+(y-2)^2}$. Como queremos encontrar o mínimo da distância entre $(x,y)$ na parábola $y=x^2+1$ e o ponto $(0,2)$, então queremos minimizar a função $f(y)=\sqrt{y-1+(y-2)^2}=\sqrt{y^2-3y+3}$, mas isso é equivalente a minimizar a função $g(y)=y^2-3y+3$ quando $y^2-3y+3>0$. Mas $g'(y)=2y-3=0 \Leftrightarrow y=\frac{3}{2}$. Além disso concluímos que $g(y)$ decresce se $y<\frac{3}{2}$ e cresce se $y>\frac{3}{2}$. Concluimos que $y=\frac{3}{2}$ é valor de mínimo e $x^2=\frac{3}{2}-1=\frac{1}{2}$. Portanto os pontos da parábola mais próximos de $(0,2)$ são: $\left(\dfrac{\sqrt{2}}{2}, \dfrac{3}{2}\right)$ e $\left(\dfrac{-\sqrt{2}}{2}, \dfrac{3}{2}\right).$
Determine dois números cuja soma seja 20 e o produto entre eles seja o maior possível.
Sejam $x$ e $y$ dois números tais que $x+y=20$. Consideremos a função produto dos números $x$ e $y$ que pode ser descrita da forma $p(x)=x(20-x)=20x-x^2$. Como $p'(x)=0 \Leftrightarrow 20-2x=0 \Leftrightarrow x=10$ e o gráfico da função $p(x)$ é uma parábola com concavidade voltada para baixo, então $p(10)=100$ é o máximo absoluto da função. Portanto $x=y=10$ são a solução do nosso problema.
Considere os retângulos inscritos na região plana delimitada pela parábola de equação $y=9-x^2$ e pelo eixo $x$ como na figura abaixo. Determine as dimensões do retângulo de área máxima.
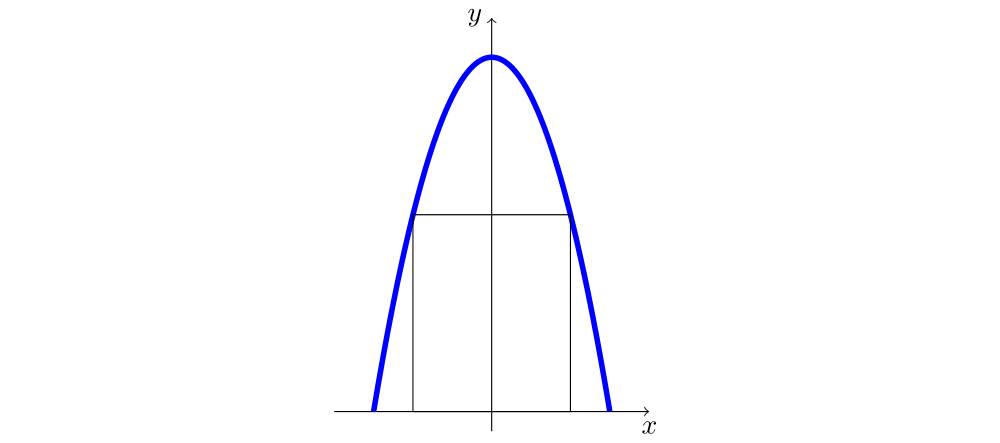
Seja $x$ a abscissa do vértice inferior direito do retângulo. Então $x \in [0,3]$ e a área do retângulo é dada pela função
$$A(x)=2x(9-x^2).$$A derivada da função área é $A'(x)=2(9-x^2)-4x^2=18-6x^2$, portanto
$$A'(x)=0 \Leftrightarrow 18-6x^2=0 \Leftrightarrow x^2=3$$e pela escolha que fizemos para $x$ concluímos que $x=\sqrt{3}$. Além disso, $A'(x)>0$ se $x \in [0,\sqrt{3})$ e $A'(x)<0$ se $x \in (\sqrt{3},3]$, portanto $x=\sqrt{3}$ é ponto de máximo local. Mas pelo Teorema de Weierstrass (note que a função $A$ é contínua em $[0,3]$) a função tem um máximo e um mínimo absolutos. Como $A(0)=A(3)=0$ e $A(\sqrt{3})=12\sqrt{3}$, concluímos que as dimensões do retângulo de área máxima são: $2\sqrt{3} \approx 3,46$ e $6$.
Um contêiner retangular aberto no topo deve ter um volume de $10 \text{ m}^3$. O comprimento de sua base é o dobro da largura. O material para a base custa $100$ reais por metro quadrado e o material para a lateral $60$ reais por metro quadrado. Determine as dimensões do contêiner de custo mínimo.
Consideremos $x$ e $2x$ as medidas da largura e comprimento da base, respectivamente, conforme a figura abaixo. Note que sendo $x$ um comprimento então $x>0$. Seja $y$ a altura do contêiner.
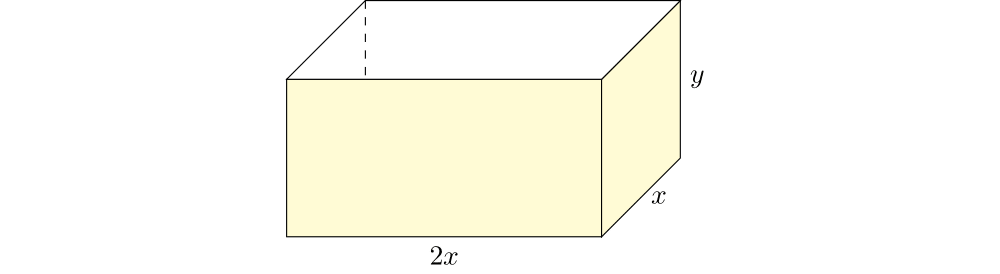
Como o volume do contêiner é $10\text{m}^3$ temos que $10=2x^2y \Leftrightarrow y= \dfrac{5}{x^2}$. Além disso a área da base é igual a $2x^2$ e a área lateral é igual a $(2x+x+2x+x)y=\dfrac{6x \cdot 5}{x^2}=\dfrac{30}{x}$. Sendo assim, a função que descreve o custo de material necessário para o fabrico do contêiner é:
$$f(x)=100 \cdot 2x^2 + 60 \cdot \dfrac{30}{x}=200x^2+\dfrac{1800}{x}.$$Então
$$f'(x)=400x-\dfrac{1800}{x^2}= \dfrac{400x^3 -1800}{x^2}.$$Nesse caso, $f'(x)=0 \Leftrightarrow 400x^3-1800=0\Leftrightarrow 2x^3-9=0\Leftrightarrow x=\sqrt[3]{\dfrac{9}{2}}.$ Além disso, $f'(x)<0$ se $x<\sqrt[3]{\dfrac{9}{2}}$ e $f'(x)>0$ se $x>\sqrt[3]{\dfrac{9}{2}}$, ou seja $x=\sqrt[3]{\dfrac{9}{2}}$ é um ponto de mínimo absoluto da função $f$. Portanto o custo de material do contêiner é mínimo quando as suas dimensões são:
$$x=2\sqrt[3]{\dfrac{9}{2}} \approx 3.30\text{m}, \quad x=\sqrt[3]{\dfrac{9}{2}} \approx 1.65\text{m} \quad \text{e} \quad y=5\left(\dfrac{2}{9}\right)^{\frac{2}{3}} \approx 1.83\text{m}.$$Pretende-se estender um cabo de uma usina de força à margem de um rio de $900$m de largura até uma fábrica que fica do outro lado do rio, $3.000$m rio abaixo. O custo para estender um cabo pelo rio é de R\($\) $5,00$ o metro, enquanto que para estendê-lo por terra custa R\($\) $4,00$ o metro. Qual o percurso mais econômico para o cabo?
Comecemos por ilustrar o problema com uma figura:
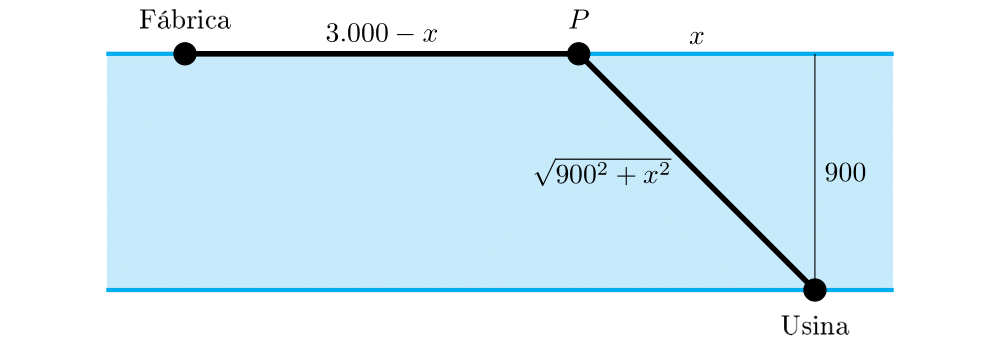
O valor que queremos minimizar é o custo de instalação do cabo, dado pela função:
$$C(x)=5\sqrt{900^2+x^2} +4(3000-x).$$Note que $x$ e $3000-x$ são medidas de comprimento, logo não podem tomar valores negativos e portanto $x \in [0,3000]$. Temos $C'(x)=\dfrac{5x}{\sqrt{900^2+x^2}}-4$, logo:
$$C'(x)=0 \Leftrightarrow \dfrac{5x}{\sqrt{900^2+x^2}}=4 \Leftrightarrow \sqrt{900^2+x^2}=\dfrac{5x}{4}.$$Mas $900^2+x^2$ e $x$ são positivos, podemos então elevar ao quadrado ambos os lados da equação anterior e obter:
$$900^2+x^2=\dfrac{25x^2}{4} \Leftrightarrow x^2=\dfrac{16 \cdot 900^2}{9} \Leftrightarrow x=\pm 1200.$$Assim, $x=1200$ é o único ponto crítico em $[0,3000]$. Como $C''(x)=\dfrac{5 \cdot 900^2}{\left(900^2+x^2\right)^{\frac{3}{2}}}>0$ para todo $x$, concluímos que $x=1200$ é ponto de mínimo local. Falta agora verificar os valores da função nos candidatos a ponto de mínimo absoluto que pode ser nos extremos do intervalo ou no ponto crítico. Como $C(0)=16500$, $C(1200)=14700$ e $C(3000) \approx 15660,$ concluímos que o custo mínimo para instalação do cabo é R\($\) $14.700,00$ e para ter esse custo devemos instalar o cabo por terra (pela margem do rio) durante $1.800$m a partir da fábrica e depois ir sobre o rio em direção à Usina.
Nos itens abaixo localize os pontos onde ocorrem os extremos absolutos das funções nos intervalos dados.
$f(x)=x^3-3x^2,\ x\in [-1,3]$
$f(x)=2\cos x +\mathrm{sen } 2x, \ x\in[0,4\pi]$
$f(x)=\dfrac{x^5}{5}-\dfrac{x^3}{3}+2 , \ x\in [-2,2]$
A função polinomial $f(x)=x^3-3x^2$ é contínua no intervalo fechado e limitado $[-1,3]$, logo $f$ satisfaz as hipóteses do Teorema dos Valores Extremos (é o teorema de Weierstrass). Aplicando esse teorema, comparamos os valores $f(-1)$ e $f(3)$ com os valores de $f$ nos pontos críticos que estão no interior de $[-1,3]$. Concluímos que: $\textrm{mín} \ f=f(-1)=f(2)=-4$ e $\textrm{máx}\ f=f(0)=f(3)=0$.
A função $f(x)=2\cos x+\mathrm{sen } 2x$ é contínua em $\mathbb{R}$ pois é a soma de produto e composta de funções contínuas em $\mathbb{R}$, logo $f$ é contínua no intervalo fechado e limitado $[0,4\pi]$. Assim, pelo Teorema de Weierstrass, comparamos os valores $f(0)$ e $f(4\pi)$ com os valores de $f$ nos pontos críticos que estão em $(0,4\pi)$. Concluímos: $\textrm{mín} \ f=f(5\pi /6)=(17\pi /6)=-3\sqrt3/2$ e $ \textrm{máx} \ f=f(\pi/6)=(13\pi/6)=3\sqrt3/2$.
A função polinomial $f(x)=\dfrac{x^5}{5}-\dfrac{x^3}{3}+2$ é contínua no intervalo fechado e limitado $[-2,2]$. Assim, pelo Teorema dos Valores Extremos, comparamos os valores $f(-2)$ e $f(2)$ com os valores de $f$ nos pontos críticos que estão em $(-2,2)$. Concluímos: $ \textrm{mín} \ f=f(-2)=-\dfrac{26}{15}$ e $\textrm{máx}\ f=f(2)=\dfrac{86}{15}$.
Ache a inclinação máxima da curva $y=x^3-3x+3$ no intervalo $\left[-\frac{3}{2},\frac{5}{2}\right]$.
A inclinação da curva em um ponto $(x,y)$ é dada por $y'=3x^2-3$. Consideremos então a função $I(x)=3x^2-3$ no intervalo $\left[-\frac{3}{2},\frac{5}{2}\right]$. Os pontos críticos da função $I$ são os pontos tais que $I'(x)=0 \Leftrightarrow 6x=0 \Leftrightarrow x=0$. Agora testando os valores de $I$ no ponto crítico e nos extremos do intervalo, vemos que:
$$I(0)=-3, \quad I\left(-\frac{3}{2}\right)=\frac{15}{4} \quad \text{e} \quad I\left(-\frac{5}{2}\right)=\frac{63}{4}$$. Logo a inclinação máxima é $63/4$.
Uma página deve conter $60 \text{ cm}^2$ de área impressa. As margens superior e inferior devem ter $3 \text{ cm}$, enquanto as laterais têm $2 \text{ cm}$ de cada lado. Encontre as dimensões da página que consomem a menor quantidade de papel.
Consideremos uma página como na figura ao lado, onde a área sombreada corresponde à área impressa. Sejam $x$ a largura e $y$ a altura, da área impressa. Então $xy=60$. Além disso, a área total da página é igual a $(x+4)(y+6)$. Consideremos então a função
$$A(x)=\left(x+4\right)\left(\dfrac{60}{x}+6\right).$$Derivando a função $A$ obtemos:
$$A'(x)=\left(\dfrac{60}{x}+6\right)-\dfrac{60(x+4)}{x^2}= \dfrac{60x+6x^2-60x-240}{x^2}= \dfrac{6(x^2-40)}{x^2}.$$Vamos agora estudar o sinal da derivada. Para isso basta ver o sinal da função do numerador para $x>0$, pois o denominador é positivo. Então,
$$A'(x)=0 \Leftrightarrow x=2\sqrt{10};A'(x)>0 \Leftrightarrow x>2\sqrt{10}; A'(x)<0 \Leftrightarrow 0<x<2\sqrt{10}.$$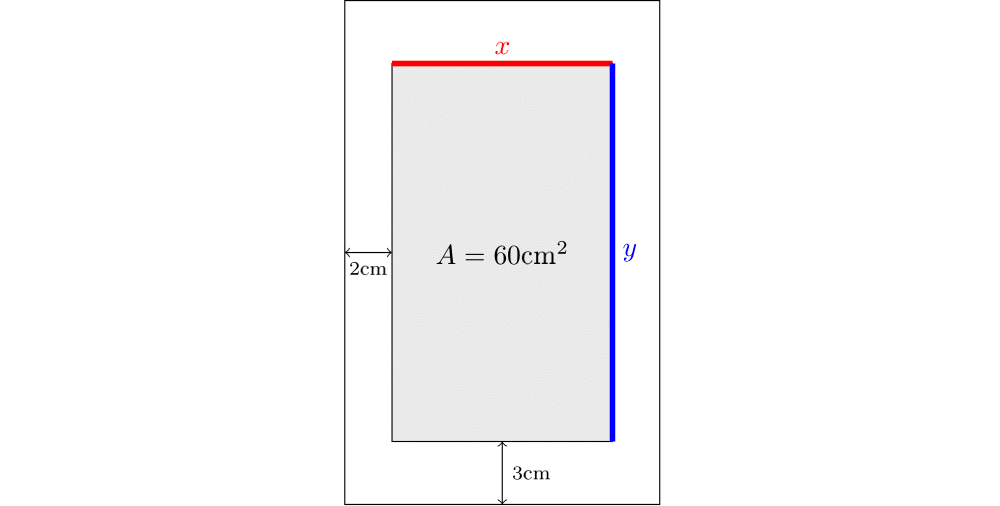
Considere os triângulos retângulos no 1º quadrante, cada um com seus lados apoiados nos eixos coordenados e em uma reta que contém o ponto $(2,3)$. Encontre o triângulo de área mínima.
Consideremos o triângulo $T$ retângulo com vértices $(0,0)$, $(x,0)$ e $(0,y)$, cuja hipotenusa contém o ponto $(2,3)$, como representado a vermelho na figura ao lado. Note que $x>2$ e $y>3$.
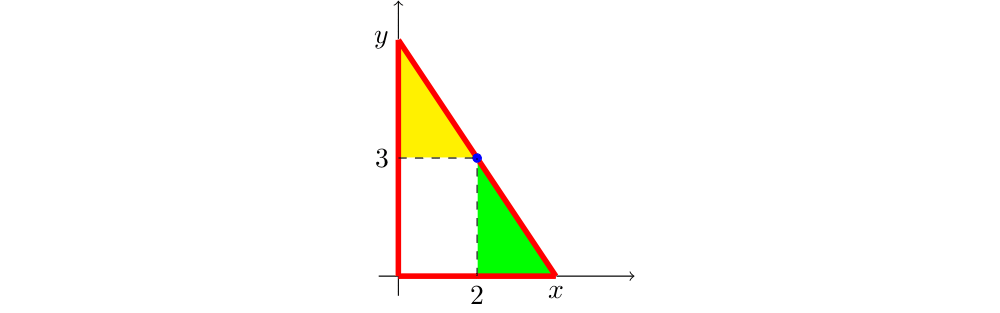
Note que os triângulos amarelo e verde são semelhantes, logo temos a relação
$$\dfrac{x-2}{2}=\dfrac{3}{y-3} \Leftrightarrow y=\dfrac{6}{x-2}+3.$$Então a área do triângulo $T$ é dada pela função:
$$A(x)=\dfrac{x y}{2} = \dfrac{x}{2} \left(\dfrac{6}{x-2}+3\right)=\dfrac{3x}{x-2} + \dfrac{3x}{2}.$$Derivando a função $A$ obtemos $A'(x)=\dfrac{-12+3(x-2)^2}{2(x-2)^2}$.
Vamos agora estudar o sinal da derivada. Para isso basta ver o sinal da função do numerador para $x>2$, pois o denominador é positivo. Então,
$A'(x)=0 \Leftrightarrow x=4;$
$A'(x)>0 \Leftrightarrow x>4;$
$A'(x)<0 \Leftrightarrow 2<x<4.$
Portanto, $x=4$ é ponto de mínimo local e absoluto para a área do triângulo $T$. Mas para $x=4$ então $y=6$. Logo $T$ tem vértices: $(0,0)$, $(4,0)$ e $(0,6)$.
Portanto, $2\sqrt{10}$ é ponto de mínimo local e absoluto para a área da página. Mas para $x=2\sqrt{10}$ então $y=3\sqrt{10}$. Logo as dimensões da página são $6+3\sqrt{10} \approx 15,49\text{ cm}$ e $4+2\sqrt{10} \approx 10,32\text{ cm}$.