
As funções são utilizadas para descrever o mundo real em termos matemáticos, é o que se chama de modelagem matemática para as diversas situações. Podem, por exemplo, descrever o ritmo cardíaco, crescimento populacional, variações de temperatura, movimento de objetos, evolução de uma epidemia, custos e lucros de uma empresa, oscilações do solo num terremoto, entre muitas outras coisas. A noção de função é a principal ferramenta para o estudo do Cálculo Diferencial e Integral, pois constitui o ambiente no qual o Cálculo é desenvolvido.
Dentre as funções mais importantes, destacamos as polinomiais, as funções racionais, as funções raízes, as trigonométricas, exponenciais e logarítmicas. Nessa disciplina, vamos estudar um pouco de cada uma delas.
As funções surgem quando uma quantidade (variável dependente) depende de outra (variável independente). Observe os exemplos:
| Ano | População (bilhões) |
| 1900 | 1,650 |
| 1910 | 1,750 |
| 1920 | 1,860 |
| 1930 | 2,070 |
| 1940 | 2,300 |
| 1950 | 2,560 |
| 1960 | 3,040 |
| 1970 | 3,710 |
| 1980 | 4,450 |
| 1990 | 5,280 |
| 2000 | 6,080 |
| 2010 | 6,900 |
| 2020 | 7,790 |
Eletrocardiograma
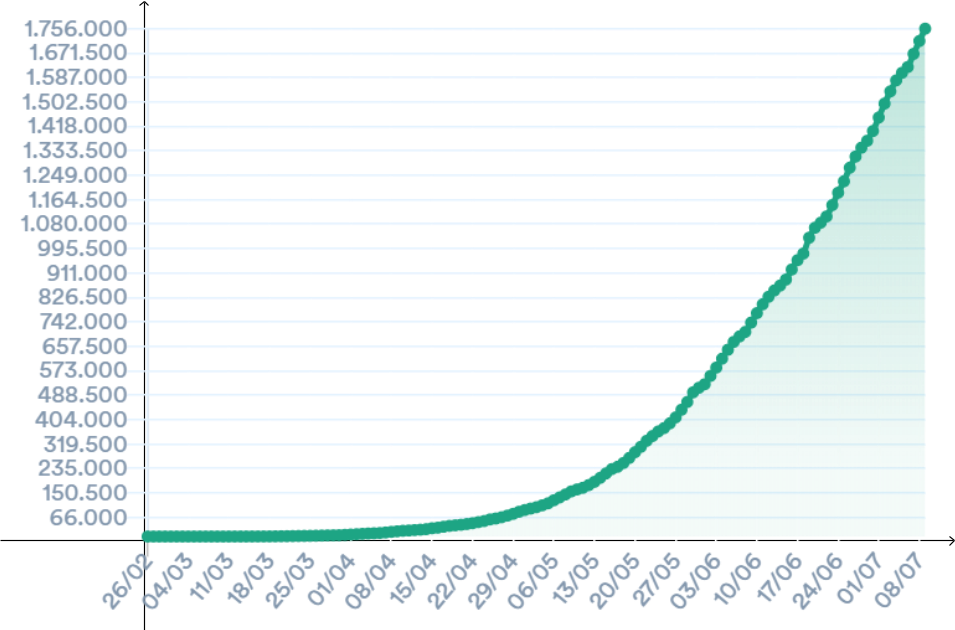
Figura 2 - Casos Acumulados de Covid-19 no Brasil em 2020 (fase exponencial). Fonte: https://covid.saude.gov.br

Figura 3 - Projeção da evolução da Covid 19
Em todos os casos acima temos uma associação que a cada valor da variável independente (tempo ou raio), atribui um único valor à variável dependente (Temperatura, Área, População, Potencial Elétrico ou Número de infectados). Essa situação constitui o que chamamos de função, cuja definição matemática é a seguinte :
Uma função de um conjunto $A\subset\mathbb{R}$ para outro conjunto $B\subset \mathbb{R}$ é uma regra (lei) que a cada elemento $x\in A$ associa um único elemento $y\in B$.
Costuma-se denotar uma função por letras como $f$ (ou $g,h,T,u,...$). E a seguinte notação, devida a Euler é utilíssima $y=f(x)$ (Lê-se "$y$ é igual a $f$ de $x$"). Outra maneira de denotar uma função é $f:A\subset\mathbb{R}\rightarrow B\subset\mathbb{R}$ ou ainda
\[\begin{array}{cccc}f : & \! A & \! \longrightarrow &\! B \\ & \! x & \! \longmapsto & \! f(x).\end{array}\]O conjunto $A$ é dito o domínio da função $f$, também denotado por $\mathrm{D}(f)$, e $B$ é dito seu contradomínio. Assim, uma função é formada por três elementos, a lei de formação, o domínio e o contradomínio.
No exemplo do applet abaixo, temos uma função de domínio $\mathbb{R}$ e contradomínio também $\mathbb{R}$. Para todo $x\in\mathbb{R}$, há único $y$ associado a ele, que denotaremos $y=f(x)$.
Observações:
Para ser considerada função, a lei deve ser capaz de associar a cada elemento do domínio um único elemento do contradomínio. Se houver ambiguidade na associação, a lei não é considerada uma função. Uma forma clássica de representar essa ideia é através de diagramas de flechas :
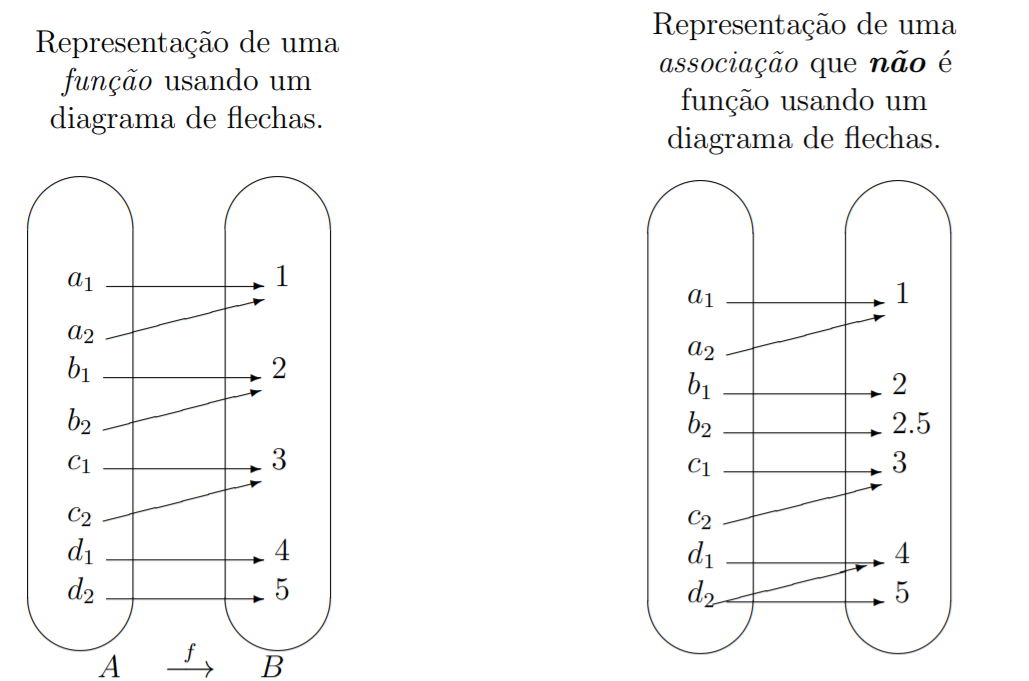
Nem toda relação entre elementos de conjuntos é uma função. Por exemplo, no applet abaixo, a relação entre $x \in [1,+\infty)$ e $y \in \mathbb{R}$ dada por $y^2−x+2y=0$ não define uma função. Mova o ponto $x$ para perceber que, para $x>-1$, existem dois valores diferentes de $y \in \mathbb{R}$ associados ao $x$, isto é, satisfzendo $y^2−x+2y=0$. Desta forma, $y$ não é único, portanto $y$ não é dado em função de $x$.
A função $f(x)=bx+c$, $x\in \mathbb{R}$, onde $b$ e $c$ são constantes reais. Ou seja, qualquer expressão do 1º grau pode ser vista como uma função real de variável real. Esse tipo de função é chamada de Função Afim}.
A função $f(x)=x^2$, $x\in \mathbb{R}$. Em geral, qualquer expressão do 2º grau, do tipo $f(x)=ax^2+bx+c, x\in \mathbb{R}$, onde $a$, $b$ e $c$ são constantes reais, $a\neq0$, pode ser vista como uma função real de variável real, dita Função Quadrática
As Funções Polinomiais, em geral, se escrevem como
\[p(x)=a_nx^n+a_{n-1}x^{n-1}+ \ldots +a_1x+a_0, \;\;x\in\mathbb{R},\]onde $n$ é um inteiro não negativo e $a_n,\ldots,a_0$ são constantes reais. Estas são funções definidas em toda a reta real $\mathbb{R}$. Para, $n=1$ temos uma função afim, $n=2$ temos uma função quadrática, vistas nos exemplos anteriores e, para $n=3$, a função é dita uma Função Cúbica.
As Funções Racionais são aquelas formadas por um quociente de polinômios, digamos, $f(x)=\dfrac{p(x)}{q(x)}$ e, neste caso, o domínio depende das raízes do polinômio do denominador, ou seja, $\mathrm{D}(f)=\{x\in\mathbb{R}; q(x) \neq0 \}$. O domínio da $f$ é o conjunto dos reais, exceto as raízes de $q(x)$, que zeram o denominador, gerando uma divisão por 0, que sabemos não estar definida no conjunto dos números reais. Casos particulares de funções racionais:
Observações:
A função Raiz Quadrada $f(x)=\sqrt{x}$, $x\geq0$. Para ser uma função real, o maior domínio que podemos ter para a função raiz quadrada é o intervalo $[0,+\infty)$. Além disso, dado $x\geq0$, está associado a ele um e só um número real positivo ou nulo, a saber $\sqrt{x}$, tal que o produto $\sqrt{x}\cdot\sqrt{x}=x$.
A função Raiz Cúbica $f(x)=\sqrt[3]{x}$, $x\in \mathbb{R}$. Para ser uma função real, o maior domínio que podemos ter para a função Raiz Cúbica é toda a reta $\mathbb{R}$. Além disso, dado $x\in \mathbb{R}$, está associado a ele um e só um número real, a saber $\sqrt[3]{x}$, tal que o produto $\sqrt[3]{x}\cdot\sqrt[3]{x}\cdot\sqrt[3]{x}=x$.
Muitas vezes, por simplicidade de linguagem (na verdade, abuso de linguagem!) não especificamos o domínio e o contradomínio de uma função ao apresentá-la, apenas sua expressão. Nestes casos, adotaremos a convenção abaixo.
Quando uma função for definida através de uma expressão, sem referência ao contradomínio, estaremos supondo que o contradomínio é $\mathbb{R}$. De forma análoga, se apresentarmos a expressão de uma função e perguntarmos sobre seu domínio, estaremos supondo que o domínio é o maior subconjunto de $\mathbb{R}$, onde a expressão está bem definida (pode ser calculada e nos fornece valores reais para $y$).
A função $f(x)=\dfrac{\sqrt{x+3}}{x-2}$ tem como domínio $\mathrm{D}(f)=[-3,2)\cup (2,+\infty)$ e contradomínio $\mathbb{R}$. De fato, para estar bem definida no conjunto dos reais, devemos ter, $x+3\geq0$ e $x-2\neq0$, portanto $x\geq-3$ e $x\neq2$, donde $\mathrm{D}(f)=[-3,2)\cup (2,+\infty)$.
A função $f(x)=\dfrac{1}{\sqrt{x}}+\sqrt{1-x}$ tem como domínio $\mathrm{D}(f)=(0,1]$ e contradomínio $\mathbb{R}$, pois nesse caso, devemos ter $x>0$, já que há uma raiz quadrada no denominador e $1-x\geq0$, por conta da segunda raiz. Portanto, $x>0$ e $x\leq 1$, significa que $\mathrm{D}(f)=(0, +\infty) \cap (-\infty,1]=(0,1]$.
A função $f(x)= \sqrt{x^2-7x+6}$ tem como domínio $\mathrm{D}(f)=(-\infty,1]\cup[6,+\infty)$ e contradomínio $\mathbb{R}$. De fato, nesse caso, devemos ter $x^2-7x+6\geq0$, já que há uma raiz quadrada. Calculando as raízes da equação $x^2-7x+6=0$, obtemos $x_1=1$ e $x_2=6$. Estudando o sinal da expressão do 2º grau, cuja parábola associada tem concavidade para cima, segue que $x^2-7x+6>0$, se e somente se, $x<1$ ou $x>6$. Portanto, $\mathrm{D}(f)=(-\infty,1]\cup[6,+\infty)$.
A função $f(x)=\sqrt{\dfrac{9-x^2}{x+1}}$ tem como domínio $\mathrm{D}(f)=(-\infty,-3]\cup(-1,3]$ e contradomínio $\mathbb{R}$. De fato, devemos ter $x+1\neq0$ e fazer o produto dos sinais entre $9-x^2$ e $x+1$, conforme a seguinte tabela de sinal:
| $(-\infty,-3)$ | $-3$ | $(-3,-1)$ | $-1$ | $(-1,3)$ | $3$ | $(3,+\infty)$ | |
| $9-x^2$ | $-$ | $0$ | $+$ | $+$ | $+$ | $0$ | $ -$ |
| $ x+1$ | $-$ | $-$ | $-$ | $0$ | $+$ | $+$ | $+$ |
| $\dfrac{9-x^2}{x+1}$ | $+$ | $0$ | $ -$ | $\nexists$ | $+$ | $0$ | $-$ |
Assim, teremos que $\mathrm{D}(f)=(-\infty,-3]\cup(-1,3]$.
Duas funções $f$ e $g$ são iguais, escrevemos $f=g$, se e só se $\mathrm{D}(f)=\mathrm{D}(g)$, possuem o mesmo contradomínio e $f(x)=g(x)$, $\forall x\in \mathrm{D}(f)$.
$f(x)=\dfrac{x^2-1}{x-1}\;$ e $\;g(x)=x+1$ são funções diferentes.
Como $\dfrac{x^2-1}{x-1}=\dfrac{(x-1)(x+1)}{x-1}=x+1, \forall x\neq1$, em uma primeira abordagem, você pode achar que estas duas funções são iguais, mas, repare que embora tenham a mesma imagem em cada ponto de $\mathbb{R}\backslash\{1\}$, as duas têm domínios diferentes! Temos $\mathrm{D}(f)=\mathbb{R}\backslash \{1\}\neq \mathbb{R}$ e $\mathrm{D}(g)=\mathbb{R}$.
O que ocorre é o seguinte: as duas funções são diferentes, porém possuem a mesma imagem em cada ponto de $\mathrm{D}(f)=\mathbb{R}\backslash\{1\}$, isto é $f(x)=g(x), \forall x \in \mathrm{D}(f)=\mathbb{R}\backslash \{1\}$.
$f(x)=\dfrac{x^4-1}{x^2+1}\;$ e $\;g(x)=x^2-1$ são funções iguais, pois $\mathrm{D}(f)=\mathrm{D}(g)=\mathbb{R}$, o contradomínio é o mesmo e fatorando o numerador e cancelando, obtemos a igualdade nas imagens, ponto a ponto:
$$\dfrac{x^4-1}{x^2+1}=\dfrac{(x^2-1)(x^2+1)}{x^2+1}=x^2-1 \text{, } \forall x\in \mathbb{R}$$.