
Seja $f:A\to B$ uma função. Lembremos que $f$ tem uma inversa, $f^{-1}:B\to A$, se e somente se $f$ e uma função bijetora (isto é a função $f$ é simultaneamente injetora e sobrejetora).
Observemos o gráfico da função $\mathrm{sen}:\mathbb{R}\to \mathbb{R}$.
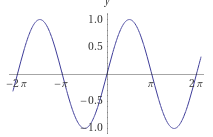
Claramente ela não é injetora pois $\mathrm{sen}(0)=\mathrm{sen}(\pi)$.
Também ela não é sobrejetora pois observando o gráfico da função vemos que sua imagem é o intervalo $[-1,1]$.
Logo a função $\mathrm{sen}:\mathbb{R}\to \mathbb{R}$ não tem inversa. Porém, podemos restringir seu domínio e seu contradomínio de forma a obter uma nova função que seja bijetora.
O seguinte gráfico representa a função $\mathrm{sen}:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]$.
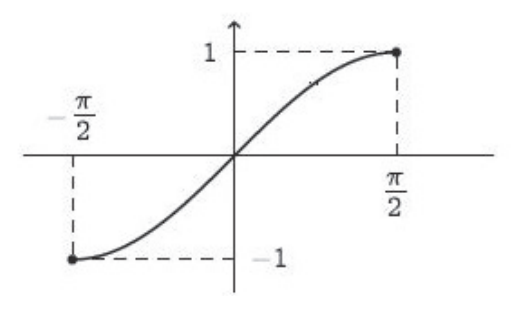
Vemos pelo gráfico que $\mathrm{sen}:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]$ é uma função bijetora e portanto ela tem uma inversa que é chamada de arcosseno e é denotada pelo símbolo $\mathrm{arcsen}$.
Então temos uma nova função:
$$\mathrm{arcsen}:[-1,1]\to \left[-\frac{\pi}{2},\frac{\pi}{2}\right]$$que tem como gráfico
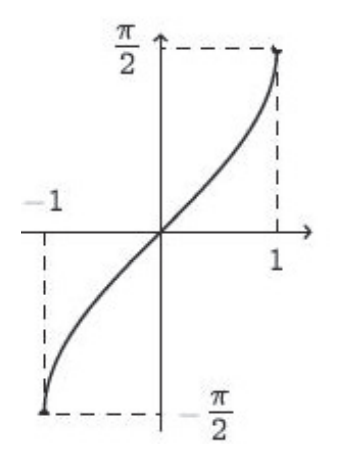
Em particular temos que $\mathrm{arcsen}$ é uma função contínua.
Observar que
$$\mathrm{arcsen}(\mathrm{sen}(x))=x ,\ \forall x\in \left[-\frac{\pi}{2},\frac{\pi}{2}\right]\ \ \text{e}\ \ \mathrm{sen}(\mathrm{arcsen}(y))=y,\ \forall y \in [-1,1].$$Ou em outras palavras:
\begin{equation}\tag{1}x = \mathrm{arcsen}(y) \text{ o único valor em } \left[-\frac{\pi}{2},\frac{\pi}{2}\right] \text{que satisfaz } \mathrm{sen}(x) = y\end{equation}Calcule $\mathrm{arcsen}\left(\frac{\sqrt{3}}{2}\right)$.
Sabemos que $\mathrm{sen}\left(\frac{\pi}{3}\right)=\frac{\sqrt{3}}{2}$, e sendo que $\frac{\pi}{3}\in \left[-\frac{\pi}{2},\frac{\pi}{2}\right]$, concluímos pela propriedade 1 que $\mathrm{arcsen}\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}$.
Calcule $\mathrm{arcsen}\left(\frac{1}{2}\right)$.
Sabemos que $\mathrm{sen}\left(\frac{\pi}{6}\right)=\frac{1}{2}$, e sendo que $\frac{\pi}{6}\in \left[-\frac{\pi}{2},\frac{\pi}{2}\right]$, concluímos pela propriedade 1 que $\mathrm{arcsen}(\frac{1}{2})=\frac{\pi}{6}$.
O gráfico da função $\cos:\mathbb{R}\to \mathbb{R}$ é
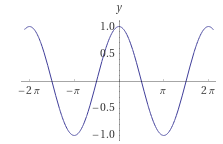
Claramente ela não é injetora pois $\cos(0)=\cos(2\pi)$.
Também, ela não é sobrejetora pois observando o gráfico da função vemos que sua imagem é o intervalo $[-1,1]$.
Logo a função $\cos:\mathbb{R}\to \mathbb{R}$ não tem inversa. Porém, podemos restringir seu domínio e seu contradomínio de forma a obter uma nova função que seja bijetora.
O seguinte gráfico representa a função $\cos:[0,\pi]\to [-1,1]$.
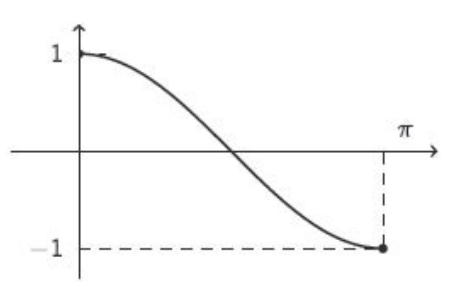
Vemos pelo gráfico que $\cos:[0,\pi]\to [-1,1]$ é uma função bijetora e portanto ela tem uma inversa que é chamada de arcocosseno e é denotada pelo símbolo $\mathrm{arcos}$.
Então temos uma nova função:
$$\mathrm{arcos}:[-1,1]\to [0,\pi]$$O gráfico de $\mathrm{arcos}(x)$ é
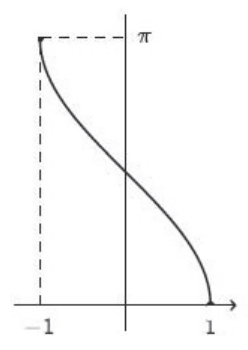
Notar que a função $g(y)=\mathrm{arcos}(y)$ é uma função contínua.
E temos que
$$\mathrm{arcos}(\cos(x))=x,\ \forall x\in [0,\pi]\ \ e\ \ \cos(\mathrm{arcos}(y))=y,\ \forall y\in [-1,1].$$Ou em outras palavras:
Calcule $\mathrm{arcos}\left(-\frac{1}{2}\right)$.
Sabemos que $\cos\left(\frac{2\pi}{3}\right)=-\frac{1}{2}$, e sendo que $\frac{2\pi}{3}\in [0,\pi]$, concluímos pela propriedade 2 que $\mathrm{arcos}\left(-\frac{1}{2}\right)=\frac{2\pi}{3}$.
Calcule $\mathrm{arcos} \left(\frac{1}{\sqrt{2}}\right)$.
Sabemos que $\cos\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}}$, e sendo que $\frac{\pi}{4}\in [0,\pi]$, concluímos pela propriedade 2 que $\mathrm{arcos}\left(\frac{1}{\sqrt{2}}\right)=\frac{\pi}{4}$.
O gráfico da função $\tan:\mathbb{R}-\left\{\frac{\pi}{2}+k\pi,\ |\ k\in\mathbb{Z}\right\}\to \mathbb{R}$ é
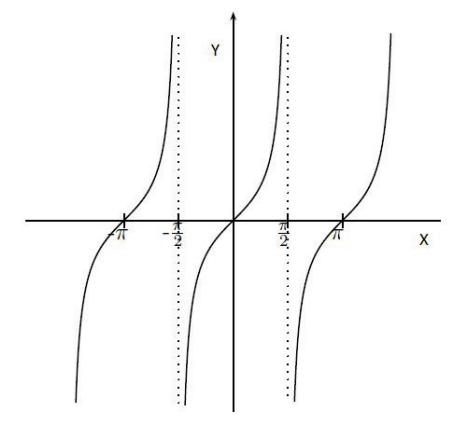
Ela é sobrejetora pois observando o gráfico da função vemos que sua imagem é todo o conjunto $\mathbb{R}$ porém ela não é injetora pois $\tan(0)=\tan(\pi)$.
Logo a função $\tan:\mathbb{R}-\{\frac{\pi}{2}+k\pi,\ |\ k\in\mathbb{Z}\}\to \mathbb{R}$ não tem inversa. Porém podemos restringir seu domínio de tal forma a obter uma nova função que seja bijetora.
O seguinte gráfico representa a função $\tan:\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\to\mathbb{R}$.
Vemos pelo gráfico que $\tan:\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\to\mathbb{R}$ é uma função bijetora e portanto ela tem uma inversa que é chamada de arcotangente e é denotada pelo símbolo $\arctan$.
Então temos uma nova função:
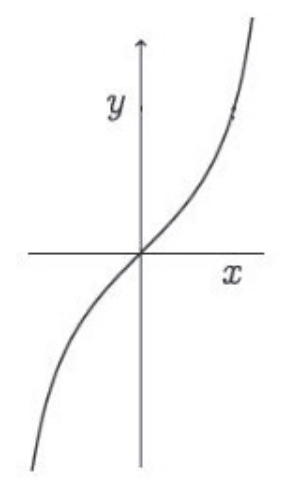
$$\arctan:\mathbb{R}\to \left(-\frac{\pi}{2},\frac{\pi}{2}\right)$$com gráfico
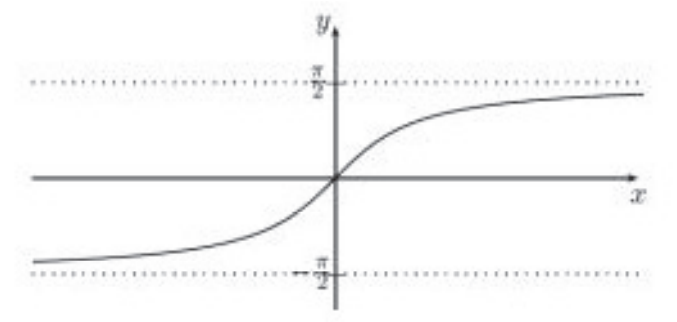
Esta função tem como domínio o conjunto $\mathbb{R}$ e sua imagem é o conjunto $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$.
Note que $f(y)=\arctan(y)$ é uma função contínua. Podemos ver pelo gráfico que
$$\lim_{y\to+\infty}\arctan y =\frac{\pi}{2}\ \ e \ \lim_{y\to-\infty}\arctan y=-\frac{\pi}{2}.$$Isto é, as retas $y=\frac{\pi}{2}$ e $y=-\frac{\pi}{2}$ são assíntotas horizontais.
Notemos que a função $f(y)=\arctan(y)$ é uma função ímpar: Logo temos
$$\arctan(-y)=-\arctan(y)\ \ \forall y\in \mathbb{R}$$Além disso temos que
$$\tan(\arctan(y))=y,\ \forall y\in \mathbb{R}\ \ e\ \ \arctan(\tan(x))=x,\ \forall x\in \left(-\frac{\pi}{2},\frac{\pi}{2}\right).$$Ou em outras palavras:
$x = \arctan(y)$ é o único valor em $\left(-\frac{\pi}{2},\frac{\pi}{2}\right)$ que satisfaz $\tan(x) = y$.