
Até o momento, temos trabalhado com funções definidas por expressões do tipo:
$$y = f(x) = \mbox{ fórmula que depende de } x \mbox{.}$$Nesse tipo de definição, vemos que a dependência de $y$ em relação a $x$ fica explícita pela expressão. Por exemplo, em $y = x^2 + 2x$, temos duas grandezas que variam: $x$ e $y$. A variação de $y$ depende da variação de $x$ e o modo como essa dependência ocorre está explícita na expressão. Nesse caso, dizemos que $y$ é uma função de $x$, definida explicitamente.
Por outro lado, se analisarmos, por exemplo, a equação $y \mathrm{sen}(xy) = 2$, vemos que, se escolhermos um valor para $x$, $y$ não pode ser arbitrariamente escolhido. Em outras palavras, os valores de $y$ que satisfazem essa expressão variam quando $x$ varia. Assim, nessa expressão, podemos pensar que $y$ depende de $x$. Se essa dependência for de tal ordem que para cada escolha de $x$ existe um único valor de $y$ satisfazendo a equação, $y$ será uma função de $x$. Mas isso não está explícito na equação. Nesse caso, dizemos que a equação define $y$ implicitamente como função de $x$.
Vamos ver outros exemplos:
\begin{array}\\y=\sqrt{1-x^2}; \\ \\f(x)=\frac{e^x}{x^2+3}; \\ \\g(z)= z\cdot \mathrm{sen}(z)+\ln(z).\end{array}Podemos observar que nos exemplos anteriores uma variável é explicitamente definida em função de outra.
Vejamos, agora, alguns casos de equações em que as relações entre variáves são dadas de uma maneira implícita:
\begin{array}\\x^2+y^2=1; \\ \\e^{f(x)}=x^2+3; \\ \\\ln(g)= z\cdot \mathrm{sen}(g\cdot z).\end{array}Quando as relações são implícitas, nem sempre é possível resolver a equação explicitando uma variável em função da outra. Às vezes, também podemos obter mais de uma solução como no caso:
$$x^2+y^2=1$$em que, resolvendo para $y$, obtemos duas soluções $y=\sqrt{1-x^2}$ e $y=-\sqrt{1-x^2}$.
Fazemos derivação implícita quando derivamos uma equação com variáveis definidas implicitamente. Para isso, a ferramenta principal é a regra da cadeia, como podemos ver no próximo exemplo.
Considere $x^2+y^2=1$ e vamos determinar $y'(x)=\frac{dy}{dx}$. Pensamos aqui que $y=y(x)$ depende de $x$ implicitamente. Primeiro derivamos ambos os lados com respeito a $x$:
$$\frac{d}{dx}(x^2+y^2)=\frac{d}{dx}{(1)},$$obtendo $2x+\frac{d}{dx}(y^2)=0$. Usando a regra da cadeia podemos escrever
$$\frac{d}{dx}(y^2)=\frac{d}{dx}{[y(x)]^2}=2\cdot y(x)\cdot\frac{d}{dx}{y(x)}=2yy'.$$Logo $2x+2yy'=0$ e resolvendo para $y'$ obtemos $y'=-\frac{x}{y}$.
Vamos examinar alguns exemplos, um pouco mais complicados, envolvendo outras regras de derivação.
Calcule $y'(x)$ usando a derivação implícita:
Vamos derivar o lado esquerdo primeiro. Usamos a regra do produto:
$$\frac{d}{dx} [x\cdot y(x)]= \frac{d}{dx} (x) \cdot y(x)+x\cdot \frac{d}{dx}[y(x)]=y+xy'.$$Agora, derivamos o lado direito usando a regra da cadeia com respeito à composição de $\sqrt{()}$ e $x+y$, lembrando que $\frac{d}{dx}\sqrt{x}= \frac{1}{2\sqrt{x}}$.
$$ \frac{d}{dx}\left[\sqrt{x+y(x)}\right]=\frac{1}{2\sqrt{x+y}}\cdot \frac{d}{dx}[x+y(x)]=\frac{1}{2\sqrt{x+y}}\cdot (1+y')=\frac{1}{2\sqrt{x+y}}+\frac{y'}{2\sqrt{x+y}}.$$Igualando ambos os lados
$$y+xy'= \frac{1}{2\sqrt{x+y}}+\frac{y'}{2\sqrt{x+y}}.$$O objetivo final é resolver para $y'$, entao manipulamos a última equação juntando os termos envolvendo $y'$ para o mesmo lado.
$$xy'-\frac{y'}{2\sqrt{x+y}}=\frac{1}{2\sqrt{x+y}}-y.$$Isolando $y'$ e juntando as frações obtemos
$$y'\left(x-\frac{1}{2\sqrt{x+y}}\right)=\frac{1}{2\sqrt{x+y}}-y,$$ $$y'\left(\frac{2x\sqrt{x+y}-1}{2\sqrt{x+y}}\right)=\frac{1-2y\sqrt{x+y}}{2\sqrt{x+y}}.$$Finalmente
$$y'=\frac{1-2y\sqrt{x+y}}{2x\sqrt{x+y}-1}.$$Para o lado esquerdo obtemos via a regra da cadeia,
$$\frac{d}{dx} [\mathrm{sen}(x\cdot y)]=\cos(x y)\cdot \frac{d}{dx}[x\cdot y(x)]=\cos(x y)(y+xy').$$Agora para o lado direito temos que usar a regra do quociente junto com a derivação implícita:
$$\frac{d}{dx}\left[\frac{x}{y(x)}\right]=\frac{1\cdot y-x\cdot \frac{d}{dx} [y(x)]}{y^2}=\frac{y-xy'}{y^2}.$$Igualando ambos os lados
$$\cos(x\cdot y)\cdot (y+xy')=\frac{y-xy'}{y^2}.$$Multiplicando e depois juntando os termos envolvendo $y'$ para o mesmo lado
$$xy'\cos(xy)+\frac{xy'}{y^2}=\frac{1}{y}-y \cos(xy).$$Isolando $y'$ e juntando termos sobre o mesmo denominador
$$y'\left(x\cos(xy)+\frac{x}{y^2}\right)=y'\left(\frac{y^2x\cos(xy)+x}{y^2}\right)=\frac{1}{y}-y\cdot \cos(xy).$$E finalmente resolvendo para $y'$ e simplificando
$$y'=\frac{y(1-y^2\cos(xy))}{x(y^2\cos(xy)+1)}.$$Usando a derivação implícita podemos calcular as equações das retas tangentes para curvas no plano, como mostra o seguinte exemplo.
Encontre as equações das retas tangentes à curva $4x^2+2xy+4y^2=1$ (uma elipse) que sejam horizontais.
Primeiro calculamos $y'$ usando a derivação implícita derivando ambos os lados
$$8x+2(y+xy')+8y\cdot y'=0.$$Resolvendo para $y'$ vamos obter
$$y'=\frac{-8x-2y}{2x+8y}.$$Para a reta tangente ser horizontal temos que $y'=0$ e logo $-8x-2y=0 \Leftrightarrow y=-4x$. Substituindo $y=-4x$ dentro da equação original obtemos
$$4x^2+2x(-4x)+4(-4x)^2=1.$$Então $60x^2=1$ e podemos determinar que $x=\frac{1}{2\sqrt{15}}$ ou $x=-\frac{1}{2\sqrt{15}}$. Usando que $y=-4x$, obtemos $y=-\frac{2}{\sqrt{15}}$ ou $y=\frac{2}{\sqrt{15}}$ respectivamente. Concluímos que temos duas retas tangentes horizontais, sendo cada uma tangente à elipse nos pontos $\left(\frac{1}{2\sqrt{15}}, -\frac{2}{\sqrt{15}}\right)$ e $\left(-\frac{1}{2\sqrt{15}}, \frac{2}{\sqrt{15}}\right)$. Como a inclinação é zero, as equações dessas retas são $y= -\frac{2}{\sqrt{15}}$ e $y=\frac{2}{\sqrt{15}}$.
Nessa seção vamos estudar problemas que dizem respeito, em algum sentido, a aplicações do cálculo. Veremos que, com base no contexto da aplicação, podemos agrupar esses problemas em classes diferentes.
Para entender a noção geral das taxas relacionadas, vamos supor que temos duas quantidades representadas por $y$ e $x$, inter-relacionadas por meio de alguma equação (por exemplo: $y\cdot x=1$. Mas, suponhamos também que $y$ e $x$ dependem do tempo $t$: $y(t)$, $x(t)$. Lembramos que as derivadas $\frac{dy}{dt}$, $\frac{dx}{dt}$ representam as velocidades ou taxas de variação dessas quantidades. Usando a regra da cadeia, podemos derivar a equação original com respeito a $t$ e determinar a relação entre as taxas $\frac{dy}{dt}$ e $\frac{dx}{dt}$. Por isso, usamos a denominação: taxas relacionadas. Vamos olhar o próximo exemplo em que um objeto se desloca ao longo de uma curva.
Imagine uma mosca andando sobre uma mesa ao longo de alguma trajetória. Suponha que o movimento pode ser modelado por uma hipérbole $x\cdot y=1$. Se no ponto $(1,1)$ a velocidade horizontal da mosca é de $10 cm/s$, calcule a velocidade vertical.
Nesse caso, ambas as variáveis - $x$ e $y$ - dependem do tempo $t$: $y(t)$, $x(t)$. Derivamos os dois lados da equação $x(t)\cdot y(t)=1$ com respeito a $t$ (usamos a regra do produto):
$$ \frac{dx}{dt}\cdot y(t)+ x(t)\cdot \frac{dy}{dt}=0.$$Resolvemos para $\frac{dy}{dt}$ representando a velocidade vertical,
$$ \frac{dy}{dt}=- \frac{y(t)}{x(t)}\cdot \frac{dx}{dt}.$$No ponto $(1,1)$, temos $x(t)=1, y(t)=1$, e $\frac{dx}{dt}= 10$. Então, nesse ponto,
$$\frac{dy}{dt}=-\frac{1}{1}\cdot 10=-10 \ cm/s,$$ou seja, a velocidade vertical é $-10 cm/s$.
Vamos agora supor que a mosca segue uma curva mais complicada como: $x^3\cdot y^3=\frac{x+y}{2}$.} Nesse caso, derivando (usando as regras do produto e da cadeia) ambos os lados com respeito a $t$ obtemos
$$\left[3x^2\frac{dx}{dt}\right]\cdot y^3+x^3\cdot\left[3y^2\frac{dy}{dt}\right]=\frac{1}{2}(\frac{dx}{dt}+\frac{dy}{dt}).$$O resto do cálculo, para esse caso, não apresenta dificuldade.
A distância entre dois pontos pode ser calculada usando o teorema de Pitágoras e no próximo exemplo estamos interessados na taxa de variação (velocidade) dessa distância.
Dois carros saem do mesmo ponto e no mesmo instante. Um carro se desloca para o sul com velocidade $60 \ km/h$ e outro, para leste com velocidade $80 \ km/h$. Determine a taxa de variação da distância entre os dois carros uma hora depois.
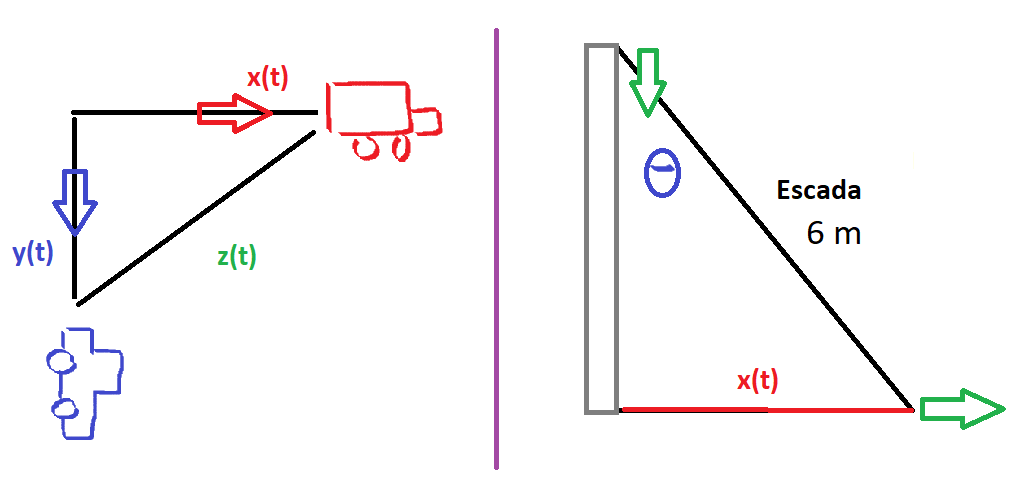
Exemplos 5 e ???
Suponha que $x(t)$ é a posição do carro no tempo $t$ que se desloca para leste e $y(t)$ é a posição do carro que se desloca para sul (veja Figura 5). Então a distância $z(t)$ entre os dois é dada pelo o teorema de Pitágoras
$$z(t)^2=x(t)^2+y(t)^2.$$Estamos interessados em calcular $\frac{dz}{dt}$ em $t=1$. Derivando os dois lados com respeito a $t$,
$$2z(t) \cdot \frac{dz}{dt}(t)=2x(t)\cdot \frac{dx}{dt}+2y(t)\cdot \frac{dy}{dt},$$ $$\frac{dz}{dt}(t)=\frac{1}{z(t)}\cdot \left(x(t) \frac{dx}{dt}+y(t) \frac{dy}{dt}\right).$$Em uma hora $x(1)=60$, $y(1)=80$ e usando o teorema de Pitágoras
$$z(1)=\sqrt{60^2+80^2}=\sqrt{10000}=100.$$Sabemos que $\frac{dx}{dt}=60$ e $\frac{dy}{dt}=80$ são constantes e logo,
$$\frac{dz}{dt}(1)=\frac{1}{100}\cdot(60\cdot 60+80\cdot 80)=\frac{1}{100}\cdot 10,000=100 \ km/h.$$Agora, se supusermos que o carro que se desloca para o sul saiu duas horas antes do outro, como a solução seria alterada?
Nessa classe de exercícios podemos ter variações envolvendo pessoas andando, trens se deslocando, aviões, e até escadas caindo. No exemplo anterior as taxas relacionadas eram as velocidades dos lados do triângulo reto formado por $x(t)$, $y(t)$, e $z(t)$. Mas também podemos perguntar sobre as relações entre as taxas de um lado e algum ângulo, como mostra o exercício seguinte.
Uma escada com $6$m de comprimento está apoiada em uma parede vertical (veja Figura 5). A extremidade inferior está escorregando e se afastando da parede a uma velocidade de 1 m/s. Calcule a velocidade do ângulo entre a parede e a escada quando a extremidade inferior se encontra a $3$m da parede.
Suponha que $x(t)$ é a distância horizontal entre a extremidade inferior da escada no tempo $t$ e a parede. Analogamente, $y(t)$ é a distância vertical entre a extremidade superior e o chão. Podemos formar a equação $x(t)^2+y(t)^2=6$, mas nesse exemplo ela não é tão útil pois estamos interessados no ângulo $\theta(t)$ (veja Figura 5). Será que usamos $\mathrm{sen}(\theta), \cos(\theta)$ ou $\mathrm{tg}(\theta)$? Sabemos que a velocidade horizontal é $\frac{dx}{dt}=1 \ m/s$. Então a equação relevante que envolve somente $x(t)$ e $\theta(t)$ é
$$\mathrm{sen}(\theta(t))=\frac{x(t)}{6},$$ou $x(t)=6sen(\theta(t))$. Derivando ambos os lados com respeito a $t$
$$\frac{dx}{dt}=6\cos(\theta)\cdot \frac{d\theta}{dt}.$$Temos que calcular $\cos(\theta)$ quando a escada está a $3$m da parede. Usando o teorema de Pitágoras, $3^2+y^2=6^2$ e logo $y=\sqrt{6^2-3^2}=3\sqrt{3}$. Então $\cos(\theta)=\frac{3\sqrt{3}}{6}=\frac{\sqrt{3}}{2}$. Como $\frac{dx}{dt}=1$ substituindo na equação obtemos
$$1=6\cdot \frac{\sqrt{3}}{2}\frac{d\theta}{dt} \ \text{ou} \ \frac{d\theta}{dt}=\frac{1}{3\sqrt{3}} \ rad/s.$$O problema seguinte envolve um cilindro e, nesse caso, as taxas relacionadas serão: as velocidades de crescimento do volume e da altura.
Uma caixa de água cilíndrica de raio $5$m e altura $10$m recebe água com velocidade $5 \ m^3/min$. Qual é a velocidade de crescimento da altura da água?
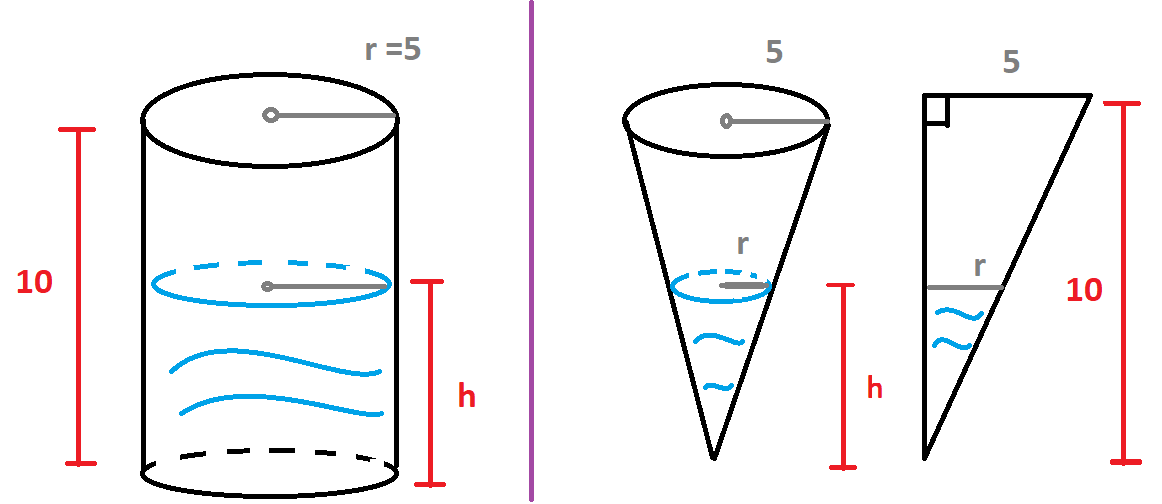
Exemplo 7
Lembramos que o volume de um cilindro é $V=\pi r^2 h$. Qual é o volume da água dentro da caixa? Nesse caso, $r=5$ e não depende do tempo $t$. Mas $V$ e $h$ dependem do tempo e logo o volume da água no tempo $t$ é $V(t)=25 \pi \cdot h(t)$ (veja Figura 7). Derivando com respeito a $t$,
$$\frac{dV}{dt}=25 \pi \cdot \frac{dh}{dt}.$$Aqui $\frac{dh}{dt}$ é a velocidade de crescimento da altura da água. Como $\frac{dV}{dt}=5$, podemos concluir que
$$\frac{dh}{dt}=\frac{1}{5\pi} \ m/min.$$Agora suponha que a caixa não é mais cilíndrica mas tem o formato de um cone. Como será alterada a solução?
Bem, o volume da água dentro da caixa cônica é $V=\frac{1}{3} \pi r^2 h$. Mas, nesse caso, todas as variáveis $V, h$, e $r$ dependem de $t$: $V(t)=\frac{1}{3} \pi r(t)^2 h(t)$. Temos duas incógnitas $r(t)$ e $h(t)$ mas temos uma relação entre a altura e o raio da caixa usando triângulos semelhantes (veja Figura 7). Obtemos
$$\frac{r}{5}=\frac{h}{10}$$e logo $r(t)=\frac{h(t)}{2}$. Deixamos como exercício substituir $r(t)=\frac{h(t)}{2}$ na equação de $V(t)$, derivar, e resolver para $\frac{dh}{dt}$.
No exemplo anterior, nosso interesse foi na relação entre crescimento do volume e o crescimento da altura do cilindro e do cone. Mas existem problemas análogos quando a figura geométrica é uma esfera e a outra variável é o raio. Poderia, também, ser um círculo e as taxas relacionadas seriam a área e o raio. Um outro caso é quando temos um cubo em dimensão três ou retângulo no plano e a outra variável é o comprimento dos lados.