
A figura a seguir contém o gráfico de uma função. Identifique, pelo menos, dois intervalos distintos em que essa função é inversível. Identifique algum intervalo em que a função não é inversível. Encontre uma característica comum no comportamento da função em todos os intervalos em que não é possível inverter a função.
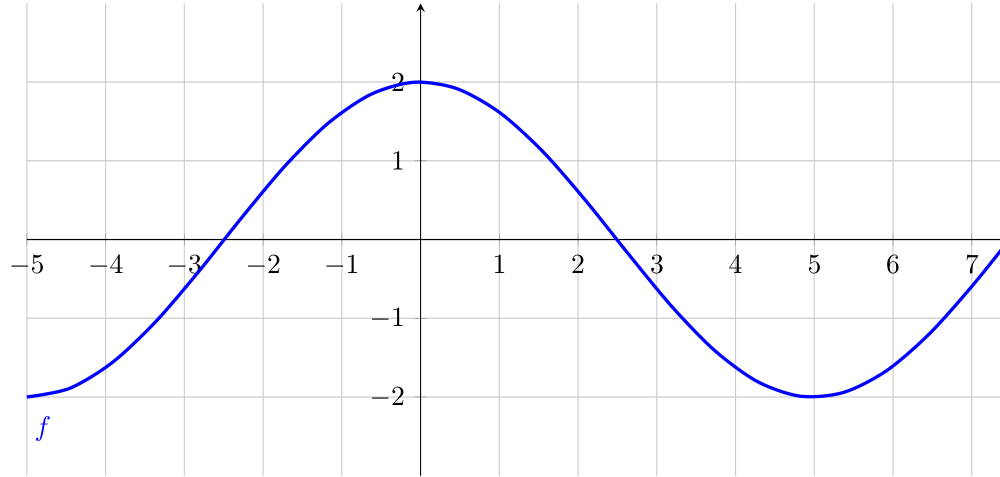
Existem infinitos intervalos em que a função é inversível. Por exemplo, $(-3,0)$ e $(2,5)$. Ela não tem inversa em $(-1,1)$ pois não é injetora nesse intervalo. Note que a função perde a injetividade, quando deixa de ser monótona. Portanto, uma característica da função nesses intervalos é a perda de monotonicidade. Note que isso aparece representado no gráfico como uma espécie platô (ou pico) - como nos pontos $(0,2)$ ou ($5,-2)$ - aonde a função, se vinha crescendo, decresce; se vinha decrescendo, passa a crescer.
Considere a função
$$f(x) = \dfrac{x+1}{x-2}, \quad x \in \mathbb{R}, \ \ x \neq 2.$$Determine o maior intervalo em que a função é inversível. Determine o domínio da inversa para esse intervalo. Obtenha a expressão da inversa.
Começamos por verificar a injetividade. Suponha que existem $x_1$ e $x_2$ tais que $f(x_1)=f(x_2)$, ou seja,
$$\dfrac{x_1+1}{x_1-2} = \dfrac{x_2+1}{x_2-2}.$$Então:
\[\begin{array}{1c1}(x_1+1)(x_2-2)=(x_2+1)(x_1-2) \\x_1x_2-2x_1+x_2-2=x_2x_1-2x_2+x_1-2 \\x_2-x_1=-2(x_2-x_1) \\x_1=x_2\end{array}\]Concluímos que a função é injetora em todo seu domínio (ou seja em $\mathbb{R}- \{2\}$).
A função tem uma assíntota vertical em $x= 2$ e uma assíntota horizontal em $y=1$. Com efeito, se $x \to 2^{-}$, $f(x) \to -\infty$ Se $x \to -\infty$, $f(x) \to 1$. Como $f$ é uma função continua no intervalo $(-\infty,2)$, pelo Teorema do Valor Intermediário, concluímos que a imagem de $f(x)$ contém o intervalo $(-\infty,1)$. Uma análise análoga, permite concluir que $(1,\infty) \subset {Im}(f)$ (conjunto imagem de $f$). É fácil ver que $f$ não assume o valor $1$. Portanto $f$ é sobrejetora em $(-\infty,1) \cup (1, \infty)$. Então, $f$ é inversível em $\mathbb{R} -\{2\}$ com imagem em $\mathbb{R} -\{1\}$. Essa imagem é o domínio da inversa. Nesse caso é possível obter uma expressão para a função inversa expressando $x$ em função de $y$, da seguinte forma:
$$y=\dfrac{x+1}{x-2} \Rightarrow yx-2y=x+1 \Rightarrow yx-x=2y+1 \Rightarrow x=\dfrac{2y+1}{y-1}.$$Assim, temos
$$f^{-1}(y) = \left(\frac{2y+1}{y-1}\right), \ y \neq 1.$$Decida se a função $f^{-1}(y) = \mathrm{arcsen} (\ln (y^2))$ pode ser inversa de $f(x) = \sqrt{e^{\mathrm{sen}(x)}}$ em algum domínio.
Vamos compor as duas funções para verificar. Note que não estamos especificando domínio.
\[\begin{array}( f^{-1} \circ f(x) & = \mathrm{arcsen}\left(\ln{\left( \sqrt{e^{\mathrm{sen}(x)}} \right)}^2\right) \\& = \mathrm{arcsen}\left(\ln\left(e^{\mathrm{sen}(x)}\right)\right) \\& = \mathrm{arcsen}(\mathrm{sen}(x)) = x\end{array}\]E, portanto, a resposta é sim, desde que sejam escolhidos conjuntos para domínio e contradomínio aonde a função seja bijetora.
Obtenha a função inversa de $y = f(x) = \dfrac{1}{x}$, $x \neq 0$.
$f^{-1}(y) = \dfrac{1}{y} \;\; \; \; y \neq 0 $
Se $f$ e $g$ são duas funções inversíveis, com domínio em um conjunto $D$, então $f+g$ é inversível? E $fg$?
Nem $f+ g$ nem $fg$ são necessariamente inversíveis. Para contra-exemplo da soma, escolha $f= -g$. No produto, basta tomar $f(x) = x$, $x>1$ e $g(x) = \dfrac{1}{x}$, $x>1$.
O conjunto de pares $\{(2,-1), (3,3), (4,5), (\pi,4)\}$ está contido no gráfico de uma função contínua e inversível $f$. Qual(is) afirmação(ções) é(são) verdadeira(s)?
$(5,4)$ é um ponto no gráfico da inversa de $f$.
Existe pelo menos um ponto em comum nos gráficos de $f$ e $f^{-1}$.
$\pi$ está na imagem de $f^{-1}$.
$5/2$ é um ponto no domínio de $f^{-1}$.
Todas são verdadeiras. Vamos justificar cada uma:
Sim, porque $(4,5)$ está no gráfico da função.
Sim, pois $(3,3)$ com certeza está no gráfico de ambas, uma vez que esses gráficos são simétricos em relação à reta $y=x$.
Sim, porque $\pi$ está no domínio de $f$.
Sim. Observe que $f(2) = -1$ e $f(3) = 3$. Então, pelo Teorema do Valor Intermediário, $f$ assume todos os valores entre $-1$ e $3$.
Um dos objetivos dessa pergunta é o desenvolvimento da redação em matemática. Procure escrever a resposta como se estivesse dando uma explicação em um livro de matemática, antes de ler o gabarito. O gabarito apresenta uma possibilidade para a redação dessa resposta, mas não a única. Tente fazer da sua maneira:
$f: \mathbb{R} \longrightarrow \mathbb{R}$ e $g: \mathbb{R} \longrightarrow \mathbb{R}$ são duas funções inversíveis. Discuta a inversibilidade de $f\circ g$.
Vamos discutir passo por passo.
$f\circ g$ é bem definida em $\mathbb{R}$: Com efeito, dado $x \in \mathbb{R}$, queremos justificar que $x$ está no domínio de $f\circ g$. Para isso, observe que $x$ pertence ao domínio de $g$, pois o domínio de $g$ é $\mathbb{R}$. Ainda mais, $g(x) \in \mathbb{R}$ por hipótese, e, como o domínio de $f$ é $\mathbb{R}$, então $g(x)$ também pertence ao domínio de $f$. Portanto, $x$ pertence ao domínio de $f\circ g$.
A imagem de $f\circ g $ é $\mathbb{R}$: Com efeito, dado $a \in \mathbb{R}$, queremos ver que $a\in \Im(f\circ g)$ (imagem $f\circ g$). Para isso, como $f$ é inversível em $\mathbb{R}$, existe $z \in \mathbb{R}$ tal que $z = f^{-1}(a)$. Da mesma forma, pela inversibilidade de $g$, podemos tomar $y = g^{-1}(z)$. Então,
$$f\circ g (y) = f \circ g (g^{-1}(z)) = f(f^{-1}(a)) = a$$logo, $f\circ g (y) = a $ e portanto $a \in Im(f\circ g)$ como queríamos ver.
Pelo item anterior, sabemos que $f \circ g$ é sobrejetora com imagem em $\mathbb{R}$.
$f\circ g$ é injetora em $\mathbb{R}$: Com efeito, dados $x_1$ e $x_2$ em $\mathbb{R}$ com $x_1\not = x_2$, queremos ver que $f\circ g(x_1)\not =f\circ g(x_2)$. Mas, $g(x_1) \neq g(x_2)$ já que $g$ é inversível, e como $f$ é inversível (portanto, injetora) então também $f(g(x_1)) \neq f(g(x_2))$.
Portanto, pelos itens anteriores, $f \circ g$ é bem definida e inversível em $\mathbb{R}$. Por último, notamos que
$$(f\circ g) \circ (g^{-1} \circ f^{-1}) = f\circ (g \circ g^{-1}) \circ f^{-1} = f \circ \mathrm{id} \circ f^{-1} = f \circ f^{-1} = \mathrm{id},$$onde $\mathrm{id}$ é a função identidade nos reais (ou seja, $\mathrm{id}(x)=x$). Portanto, a inversa de $f \circ g$ é $g^{-1} \circ f^{-1}$.
Calcule:
$\mathrm{arcsen}(\frac{-1}{2})$
$\cos(\mathrm{arctg}(-1))$
$\mathrm{arccos}(\cos (\frac{43}{6}\pi))$
$\mathrm{sen}(\mathrm{arcsen} \frac{3}{5} + \mathrm{arcsen} \frac{2}{3})$
$\mathrm{arcsen}(\frac{-1}{2})=-\pi/6$, pois $\mathrm{sen}(-\pi/6)=-\mathrm{sen}(\pi/6)=-1/2$ e $-\pi/6\in [-\frac{\pi}{2},\frac{\pi}{2}]$.
$\cos(\mathrm{arctg}(-1)) = \cos\left(\dfrac{-\pi}{4}\right) = \dfrac{1}{\sqrt{2}}$
$y=\mathrm{arctg}(-1) \quad \iff \quad \mathrm{tg}(y)=-1$
Impondo a condição $y\in [-\frac{\pi}{2},\frac{\pi}{2}]$ obtemos $y=\frac{-\pi}{4}$
Quer dizer, $\mathrm{arctg}(-1)=\frac{-\pi}{4}$ = $\cos(\dfrac{-\pi}{4})= \dfrac{1}{\sqrt{2}}$Lembrar que $\arccos:[-1,1]\to [0,\pi]$ é a inversa de $\cos: [0,\pi]\to[-1,1]$. Em particular temos
$$\arccos(\cos(\alpha))=\alpha\textrm{ se }\alpha\in [0,\pi].$$Mas observe que $\frac{43}{6}\pi\not\in [0,\pi]$. Logo é incorreto dizer que $\arccos(\cos (\frac{43}{6}\pi))=\frac{43}{6}\pi$. Por outro lado sabemos que $y = \mathrm{arcsen}(x)$ é o único numero real $y\in[0,\pi]$ que satisfaz $\cos(y) = x$. Então, se queremos calcular $\arccos(\cos (\frac{43}{6}\pi))$, temos que encontrar o único numero real $y\in [0,\pi]$ tal que $\cos(y)=\cos (\frac{43}{6}\pi)$. Para fazer isto procedemos da seguinte forma:
Como $\cos:\mathbb{R}\to \mathbb{R}$ é periódica de período $2\pi$ temos
$$\cos\left(\frac{43}{6}\pi\right)=\cos \left(\frac{43}{6}\pi+2\pi k\right)\quad \text{para todo $k\in\mathbb{Z}.$}$$Então é só encontrar esse único inteiro $k_{0}$ tal que
$$\frac{43}{6}\pi+2\pi k_{0}\in [0,\pi],$$e a solução seria $y=\frac{43}{6}\pi+2\pi k_{0}$. Fazemos então
$$\frac{43}{6}\pi=\frac{6.6+7}{6}\pi=\left(6+\frac{7}{6}\right)\pi=6\pi+\frac{7}{6}\pi.$$Logo $\frac{43}{6}\pi=6\pi+\frac{7}{6}\pi$, e por tanto
$$\cos\left(\frac{43}{6}\pi\right)=\cos\left(6\pi+\frac{7}{6}\pi\right)=\cos\left(\frac{7}{6}\pi\right).$$Notemos que $\frac{7}{6}\pi\not\in [0,\pi]$, logo é incorreto dizer que $\arccos(\cos (\frac{43}{6}\pi))=\frac{7}{6}\pi$. Porém $\frac{7}{6}\pi=2\pi-\frac{5}{6}\pi$, logo
$$\cos\left(\frac{43}{6}\pi\right)=\cos\left(\frac{7}{6}\pi\right)=\cos\left(2\pi-\frac{5}{6}\pi\right)=\cos\left(-\frac{5}{6}\pi\right)=\cos\left(\frac{5}{6}\pi\right).$$Notemos que $\frac{5}{6}\pi\in [0,\pi]$. Assim, temos achado o único numero real em $y\in[0,\pi]$ que satisfaz $\cos(y)=\cos (\frac{43}{6}\pi)$, e portanto $\arccos(\cos (\frac{43}{6}\pi))=\frac{5}{6}\pi$.
Sabemos que $\mathrm{sen}(\alpha+\beta)=\mathrm{sen}(\alpha)\cos(\beta)+\cos(\alpha)\mathrm{sen}(\beta)$ para todo $\alpha,\beta\in\mathbb{R}$. Tomando, em particular os valores $\alpha=\mathrm{arcsen}(3/5)$ e $\beta=\mathrm{arcsen}(2/3)$ temos que $\mathrm{sen}(\alpha)=3/5$ e $\mathrm{sen}(\beta)=2/3$. Então
\begin{eqnarray}{} \tag{1} &(1)&\\ &\downarrow&\\\mathrm{sen}\left(\mathrm{arcsen} \frac{3}{5} +\mathrm{arcsen} \frac{2}{3} \right) & = & \mathrm{sen}(\alpha+\beta) = \mathrm{sen}(\alpha)\cos(\beta)+\cos(\alpha)\mathrm{sen}(\beta)\text{(Desenvolvendo o seno da soma)} \\& = & \frac{3}{5}\cos(\beta)+\cos(\alpha)\frac{2}{3} \\&\downarrow & \\& (2) & \\\end{eqnarray}$(1)\alpha:=\mathrm{arcsen}(3/5)$ e $\beta:=\mathrm{arcsen}(2/{3})$
$(2)$Observar que $\mathrm{sen}(\alpha)=3/5$ e $\mathrm{sen}(\beta)=2/3$Assim, para finalizar falta achar somente os valores $\cos(\beta)$ e $\cos(\alpha)$, isto é $\cos(\mathrm{arcsen}(2/3))$ e $\cos(\mathrm{arcsen}(3/5))$. Usamos a relação $\mathrm{sen}^2\alpha+\cos^2\alpha=1$, e sabendo que $\alpha\in [-\pi/2,\pi/2]$, temos que $\cos(\alpha)=\sqrt{1-\mathrm{sen}^2\alpha}$. Entao
$$\cos(\mathrm{arcsen} \frac{2}{3})=\sqrt{1-\mathrm{sen}^2\left(\mathrm{arcsen} \frac{2}{3}\right)}=\sqrt{1-\left(\frac{2}{3}\right)^2}=\frac{\sqrt{5}}{3}$$e
$$\cos(\mathrm{arcsen} \frac{3}{5})=\sqrt{1-\mathrm{sen}^2\left(\mathrm{arcsen} \frac{3}{5}\right)}=\sqrt{1-\left(\frac{3}{5}\right)^2}=\frac{4}{5}.$$Voltando a 1 concluímos que:
$$\mathrm{sen}\left(\mathrm{arcsen} \frac{3}{5} +\mathrm{arcsen} \frac{2}{3}\right)=\frac{3}{5}\cos(\beta)+\cos(\alpha)\frac{2}{3}=\frac{3}{5} \cdot \frac{\sqrt{5}}{3}+\frac{4}{5} \cdot \frac{2}{3}=\frac{3\sqrt{5}+8}{15}.$$Determine o domínio da função $f(x)=\dfrac{1}{\mathrm{arcsen}(|x|-4)}$.
O denominador deve ser diferente de zero. Logo devemos ter $\mathrm{arcsen}(|x|-4)\neq0$. Note também que $\mathrm{arcsen}:[-1,1]\to[-\frac{\pi}{2},\frac{\pi}{2}]$, logo $|x|-4\in[-1,1]$. Então
\begin{eqnarray}\mathrm{arcsen}(|x|-4) = 0 &\iff& \mathrm{sen}(\mathrm{arcsen}(|x|-4))=\mathrm{sen}(0)\\&\iff& |x|-4=0\\&\iff& |x|=4\\&\iff& x=4\textrm{ ou }x=-4\\\end{eqnarray}Ou seja, para que $\mathrm{arcsen}(|x|-4)\neq0$ devemos considerar os valores de $x$ tais que $x\neq4\textrm{\ e\ }x\neq-4$. Isto é, $x\in (-\infty,-4)\cup(-4,4)\cup (4,\infty).$
Por outro lado, dado que $ |x|-4\in[-1,1]$, temos
\begin{eqnarray}|x|-4\in[-1,1]& \iff& -1\le|x|-4\le1\\&\iff& 3\le|x|\le 5\\&\iff& |x|\le5\textrm{ e }|x|\ge3 \\&\iff& x\in [-5,5]\textrm{ e também } x\in (-\infty,-3]\cup[3,+\infty)\\&\iff& x\in [-5,-3]\cup[3,5].\end{eqnarray}Assim, o domínio da função $f$ dada é o conjunto
$$\big((-\infty,-4)\cup(-4,4)\cup (4,\infty)\big)\cap\big([-5,-3]\cup[3,5]\big)=[-5,-4)\cup(-4,-3]\cup[3,4)\cup(4,5].$$Os diagramas abaixo apresentam valores de uma função diferenciável $f$ e sua derivada $f'$. Sabe-se que $f$ é de classe $C^1(\mathbb{R})$
$$\begin{array}{lr}\begin{array}{lll}1 & \stackrel{f }\longmapsto &3 \\2 & \stackrel{f }\longmapsto &\sqrt{2} \\3 & \stackrel{f }\longmapsto &-5 \\4 & \stackrel{f }\longmapsto &-1\end{array} &\begin{array}{lll}1 & \stackrel{f '}\longmapsto &2 \\2 & \stackrel{f '}\longmapsto &1 \\3 & \stackrel{f '}\longmapsto &-3 \\4 & \stackrel{f '}\longmapsto & 0\end{array}\end{array}$$Em vizinhança de qual(is) valor(es) de $x$ (dentre os dados) o teorema da função inversa é inconcludente? Suponha que $f$ é globalmente inversível. Sendo $y = f(x)$, em qual valor de $y$ não podemos calcular a derivada de $f^{-1}$ pelo Teorema da Função Inversa? Calcule $(f^{-1})' (-5)$ e $(f^{-1})' (3)$.
Em $x=4$ a derivada de $f$ se anula. Assim, o Teorema da Função Inversa não afirma nada sobre uma vizinhança de $x=4$. O valor $x=4$ está associado a $y =-1$. Logo, em $y=-1$ não podemos calcular a derivada de $f^{-1}$ (se existir) pela fórmula do TFI. Usando a fórmula escrevemos
\[(f^{-1})'(-5) = \dfrac{1}{f'(3)} = - \dfrac{1}{3} \;\;\;\;\;\;\;\mbox{ e }\;\;\;\;\;\;\; (f^{-1})'(3) = \dfrac{1}{f'(1)} = \dfrac{1}{2}\]Considere $y=f(x) = \mathrm{sen}(x)$, $x \in (-\pi/2, \pi/2)$. Calcule a derivada de ${\rm arcsen}(y)$, $ y \in (-1,1)$.
Considere $\mathrm{sen}: (-\pi/2, \pi/2) \longrightarrow (-1,1)$. Sabemos que essa função é inversível e de classe $C^1$ no seu domínio. Além disso, $\mathrm{sen}'(x) = \cos(x) \neq 0 \;\;\ x\in(-\pi/2, \pi/2)$. Assim, pelo TFI, escrevemos:
\[{\rm arcsen}'(y) = \frac{1}{\cos(x)}\]sabemos que $y = \mathrm{sen}(x)$ e que $\mathrm{sen}^2(x) + \cos^2(x) = y^2 + \cos^2(x) = 1 \implies \cos^2(x) = 1- y^2$. No intervalo considerado o cosseno é positivo, de modo que podemos escrever: $\cos(x) = \sqrt{1-y^2}$. Assim:
\[{\rm arcsen}'(y) = \frac{1}{\sqrt{1-y^2}} \; \; \; \; y \in (-1,1)\]A tabela a seguir apresenta valores referentes à inversa de uma função $f \in C^1(\mathbb{R})$. Suponha que alguém aproximou (corretamente) $f(x)$ pelo polinômio deduzido na definição da derivada de $f$, na forma $ax + b$, perto de $x=1$. Calcule $a$ e $b$
$$\begin{array}{lr}\begin{array}{lll}1 & \stackrel{f^{-1}}\longmapsto &3 \\2 & \stackrel{f^{-1}}\longmapsto &\sqrt{2} \\3 & \stackrel{f^{-1}}\longmapsto &-5 \\4 & \stackrel{f^{-1}}\longmapsto &1\end{array} &\begin{array}{lll}1 & \stackrel{(f^{-1})'}\longmapsto &2 \\2 & \stackrel{(f^{-1})'}\longmapsto &1 \\3 & \stackrel{(f^{-1})'}\longmapsto &-3 \\4 & \stackrel{(f^{-1})'}\longmapsto &\sqrt{2}\end{array}\end{array}$$Se estamos trabalhando perto de $x=1$ no domínio de $f$, pela tabela, estamos em vizinhança de $y=4$ no domínio de $f^{-1}$. Usando o TFI, escrevemos
\[f'(1) =\frac{1}{(f^{-1})'(4)} = \frac{1}{\sqrt{2}}.\]Conhecemos, portanto, $f(1)$ e $f'(1)$. Usamos $f(x) \approx f(1) + f'(1)(x-1) = y(x)$ para escrever:
\[y(x) = 4 + \frac{1}{\sqrt{2}}(x-1)\]e vemos que $a = \dfrac{1}{\sqrt{2}}$ e $b = 4 - \dfrac{1}{\sqrt{2}}$
$f(x)$ é uma função de classe $C^1$ em $\mathbb{R}$. Sabe-se que $f(0) = 1$, $f(1) = -3$, $f'(0) = -2$ e $f'(1) = \sqrt{2}$. Defina $y = g(x) = f(x) + x$. Discuta a existência de uma inversa local de $g$ em vizinhança de $x=0$. Calcule $(g^{-1})'(1)$.
Por inspeção, $g(0) = 1$ e $g'(0) \neq 0$. por hipótese, $g \in C^1(\mathbb{R})$. Portanto, estamos dentro das hipóteses para as quais o TFI garante existência de inversa com $x=0$ e $y=1$. Além disso, pelo TFI:
\[(g^{-1})'(1) = \frac{1}{g'(0)} = \frac{1}{-2+1} = -1\]Calcule $y'(x)$ usando a derivação implícita:
$\tan(xy^2)=\sqrt{x}+\sqrt{y}$
$x\cdot \mathrm{sen}(y)+y\cdot \cos(x)= \frac{x+1}{y+1}$
1. Derivamos ambos os lados com respeito a $x$,
$$\mathrm{sec}^2(xy^2)\cdot[1\cdot y^2+x\cdot 2yy']=\frac{1}{2\sqrt{x}}+\frac{y'}{2\sqrt{y}}.$$Juntando os termos envolvendo $y'$ para o mesmo lado,
$$\mathrm{sec}^2(xy^2)\cdot 2xyy'-\frac{y'}{2\sqrt{y}}=\frac{1}{2\sqrt{x}}-\mathrm{sec}^2(xy^2)\cdot y^2.$$Isolando $y'$ e simplificando:
$$y'\left[\mathrm{sec}^2(xy^2)\cdot 2xy-\frac{1}{2\sqrt{y}}\right]=\frac{1-2\sqrt{x}y^2\cdot \mathrm{sec}^2(xy^2)}{2\sqrt{x}},$$ $$y'\cdot \frac{4xy^{3/2}\cdot \mathrm{sec}^2(xy^2)-1}{2\sqrt{y}}=\frac{1-2\sqrt{x}y^2\cdot \mathrm{sec}^2(xy^2)}{2\sqrt{x}}.$$Finalmente calculando $y'$,
$$y'= \frac{\sqrt{y}}{\sqrt{x}}\cdot\frac{1-2\sqrt{x}y^2\cdot \mathrm{sec}^2(xy^2)}{4xy^{3/2}\cdot \mathrm{sec}^2(xy^2)-1}.$$2. Derivamos ambos os lados com respeito a $x$,
$$\mathrm{sen}(y)+x\cdot \cos(y) \cdot y'+y'\cdot \cos(x)- y \cdot \mathrm{sen}(x)= \frac{y+1-y'(x+1)}{(y+1)^2}.$$Isolando $y'$ e simplificando:
$$y'\left(x\cdot \cos(y)+\cos(x)+\frac{x+1}{(y+1)^2}\right)=y\cdot \mathrm{sen}(x)-\mathrm{sen}(y)+\frac{y+1}{(y+1)^2}$$ $$y'=\frac{(y\cdot \mathrm{sen}(x)-\mathrm{sen}(y))(y+1)^2+(y+1)}{(x\cdot \cos(y)+\cos(x))(y+1)^2+(x+1)}.$$Encontre a equação da reta tangente à curva $y=f(x)$ definida pela equação $y^3 + 2yx^2 -3x-10=0$, no ponto $(3,1)$.
O coeficiente angular da reta tangente no ponto $x=3$ é
$$m_{T}= \dfrac{dy}{dx}(3)=f'(3).$$Derivando implicitamente a equação em relação à variável $x$ obtemos
$$3y^2 \frac{dy}{dx} + 4xy + 2x^2 \frac{dy}{dx} -3 =0,$$fazendo $x=3$ e $y=1$, tem-se
$$3 \frac{dy}{dx}(3) + 12 + 18 \frac{dy}{dx}(3) - 3 =0\ \ \Rightarrow\ \ \frac{dy}{dx}(3) = -\frac{3}{7}.$$Portanto a equação da reta tangente de $f(x)$ no ponto $(3,1)$ é
$$y-1 = f'(3)(x-3) \Leftrightarrow y-1 = - \frac{3}{7}(x-3) \Leftrightarrow y=-\frac{3}{7}x+\frac{16}{7}.$$Encontre as equações das retas tangentes à curva $x^2 + 4xy + y^2 = 6$, que sejam paralelas à reta $3x+3y=8$.
Lembre que duas retas paralelas têm o mesmo coeficiente angular. Como o coeficiente angular da reta $3x+3y=8$ é $m=-1$, então o coeficiente angular de todas as retas tangentes à curva $x^2 + 4xy + y^2 =6$ será $m_{T}=-1$. Agora, derivando implicitamente a equação em relação à variável $x$, obtemos
$$2x + 4y + 4x \frac{dy}{dx}+ 2y\frac{dy}{dx}=0 \ \ \Rightarrow\ \ \frac{dy}{dx}(x_0)=-\frac{x_0+2y_0}{2x_0 + y_0}\ \ \Rightarrow\ \ \frac{x_0+2y_0}{2x_0+y_0}=1\ \ \Rightarrow\ \ x_0=y_0.$$Como o ponto $(x_0,y_0)$ pertence à curva $x^2 + 4xy + y^2$ e $y_0=x_0$, tem-se:
$$x_0^2 + 4x_0^2 + x_0^2 = 6\ \ \Rightarrow\ \ x_0^2=1\ \ \Rightarrow\ \ x_0=1\ \text{ou}\ x_0=-1.$$Finalmente as equações das duas retas tangentes são
\begin{eqnarray} &y-1 = -(x-1) \Leftrightarrow y=-x+2\\ &y+1 = -(x+1) \Leftrightarrow y=-x-2\\ \end{eqnarray}
Mostre que a reta tangente à elipse $\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}=1$ no ponto $(x_0,y_0)$ tem a seguinte equação $\dfrac{x_0 x}{a^2}+\dfrac{y_0 y}{b^2}=1$.
Derivando implicitamente a equação da elipse em relação à variável $x$, obtemos
$$\frac{2x}{a^2}+ \frac{2y}{b^2} \frac{dy}{dx} = 0\ \ \Rightarrow\ \ \frac{dy}{dx}(x)=-\frac{x b^2}{y a^2}.$$Assim o coeficiente angular da reta tangente à elipse no ponto $(x_0,y_0)$ é $m_{T}=\dfrac{dy}{dx}(x_0)=-\dfrac{x_0 b^2}{y_0 a^2}$ e portanto a equação da reta tangente será
\begin{eqnarray} y-y_0= - \frac{x_0 b^2}{y_0 a^2}(x-x_0) \ \ & \Rightarrow & \ \frac{(y-y_0)y_0}{b^2} = - \frac{(x-x_0)x_0}{a^2} \ \Rightarrow\ \frac{(y-y_0)y_0}{b^2} + \frac{(x-x_0)x_0}{a^2}=0 \ \Rightarrow \\ & \Rightarrow &\ \frac{y_0y}{b^2} + \frac{x_0x}{a^2}=\frac{y_0^2}{b^2} + \frac{x_0^2}{a^2} {\Rightarrow} \frac{x_0 x}{a^2} + \frac{y_0 y}{b^2}=1. \end{eqnarray}
Como $(x_0,y_0)$ pertence à elipse,
temos que $\dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}=1$
Num determinado instante $t_0$, o comprimento do lado de um quadrado é de 10 centímetros.
Se cada lado do quadrado está aumentando a uma taxa de 0,2 cm/min, determine a taxa de variação da área do quadrado no instante $t=t_0$.
Agora determine a taxa de variação da área se cada lado está diminuindo a 0,4 cm/min.
Sejam $x=x(t)$ o comprimento do lado do quadrado no instante $t$ e $A(x)= x^2$ a área do quadrado. Pela hipótese, sabemos que $x(t_0)=10$.
Temos que $\dfrac{dx}{dt}(t_0)= + 0,2$ cm/min. Então a taxa de variação será
$$\dfrac{d}{dt} A(x(t_0)) = \dfrac{dA}{dx}(x(t_0)) \dfrac{dx}{dt}(t_0) = 2\ x(t_0) (0,2) = 20(0,2) = 4\ \text{cm}^2/\text{min}.$$Isto indica que a área do quadrado tem um crescimento com uma taxa de variação de $4$ cm$^2$/min no instante $t=t_0$.
Temos que $\dfrac{dx}{dt}(t_0)= - 0,4$ cm/min. Então a taxa de variação será
$$\dfrac{d}{dt} A(x(t_0)) = \dfrac{dA}{dx}(x(t_0)) \dfrac{dx}{dt}(t_0) = 2\ x(t_0) (-0,4) = 20(-0,4) = -8\ \text{cm}^2/\text{min}.$$Isto indica que a área do quadrado tem um decrescimento com uma taxa de variação de $8$ cm$^2$/min no instante $t=t_0$.
Num determinado instante $t_0$, o comprimento de um cateto de um triângulo retângulo é de $10$ cm e ele está aumentando a uma taxa de $1$ cm/min, o outro cateto tem comprimento $12$ cm e está diminuindo a uma taxa de $2$ cm/min. Calcular a taxa de variação do ângulo oposto ao cateto que tem comprimento $12$ nesse instante do tempo.
Seja $x=x(t)$ o comprimento do cateto tal que $x(t_0)=10$ e $y=y(t)$ o comprimento do cateto tal que $y(t_0)=12$.
Sabemos pelas hipóteses que $\dfrac{dx}{dt}(t_0)=+1$ e $\dfrac{dy}{dt}(t_0)=-2$.
Seja $\theta(t)$ o ângulo oposto ao cateto $y(t)$, então podemos relacionar as três funções na seguinte expressão
$$\tan (\theta(t)) = \frac{y(t)}{x(t)}.$$Derivando em relação a $t$ obtemos:
$$\sec^2 (\theta(t)) \frac{d \theta}{dt}(t)= \frac{x(t) \dfrac{dy}{dt}(t) - y(t) \dfrac{dx}{dt}(t)}{(x(t))^2}.$$No instante $t_0$, temos que: \ \ $\sec^2 (\theta(t_0))= 1 + \tan^2 (\theta(t_0))= 1 + \left(\dfrac{y(t_0)}{x(t_0)}\right)^2=1+ \left(\dfrac{12}{10}\right)^2=\dfrac{244}{100}$.
Assim: $\dfrac{d \theta}{dt}(t_0)= \dfrac{10(-2)-12(1)}{244}= - \dfrac{8}{61}$ Rad/min.
Isto indica que o ângulo está diminuindo a uma taxa de variação de $\dfrac{8}{61}$ Rad/min.
Um ponto move-se sobre a semicircunferência $x^2 + y^2 = 10$, $y \geq 0$. Suponha $\dfrac{dx}{dt}>0$. Determine o ponto da curva em que a velocidade de $y$ seja o triplo da velocidade de $x$.
Derivando a equação da semicircunferência em relação de $t$, obtemos
$$2x(t) \frac{dx}{dt} + 2y(t) \frac{dy}{dt}=0 \ \ \Leftrightarrow \ \ x(t) \frac{dx}{dt} + y(t) \frac{dy}{dt}=0.$$Pela hipótese temos que: $\dfrac{dy}{dt}=3 \dfrac{dx}{dt}$, logo
\begin{eqnarray}x(t)\frac{dx}{dt}+3y(t)\frac{dx}{dt}=0 \ \ &{\Rightarrow}& \ \ x(t)+3y(t)=0 \ \ \Rightarrow \ \ x(t)=-3y(t).\\&\downarrow& \\&\text{como } \dfrac{dx}{dt}>0&\end{eqnarray}Finalmente, substituindo na equação da semicircunferência obtemos
$$(-3y(t))^2 + (y(t))^2=10 \ \ \Rightarrow\ \ 10 (y(t))^2 = 10\ \ \Rightarrow\ \ y(t)=1.$$O ponto procurado será o ponto $(-3,1)$.
Cascalho esta caindo e formando uma pilha cônica que aumenta a uma taxa de $3 \ m^3/min$, de modo que o diâmetro do cone é sempre igual a sua altura. Encontre a taxa de variação da altura da pilha quando a altura é de $3 \ m$.
Temos que $V=\dfrac{1}{3} \pi r^2 h$. Como $2r=h$ para todo $t$ então $V(t)=\dfrac{1}{12} \pi [h(t)]^3$. Derivando com respeito ao $t$,
$$\dfrac{dV}{dt}=\dfrac{\pi}{4} \cdot h^2\cdot \frac{dh}{dt}.$$Substituindo $\frac{dV}{dt}=3$ e $h=3$, obtemos $3=\dfrac{\pi}{4} \cdot 9\cdot \dfrac{dh}{dt}$ ou que $\dfrac{dh}{dt}=\dfrac{4}{3\pi} \ m/min$.
Num determinado instante $t_0$, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto $P$ (veja a figura). Neste instante, um dos aviões está a $y_0=150$ milhas do ponto $P$ e se aproxima de $P$ a $450$ milhas por hora, enquanto o outro está a $x_0=200$ milhas do ponto $P$ e se movendo a $600$ milhas por hora, também em direção ao ponto $P$.
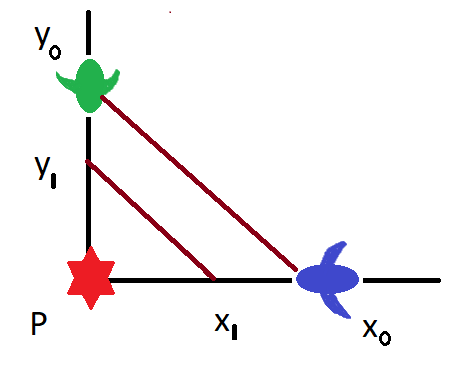
Calcule a taxa de variação da distância entre os aviões no instante $t_0$.
Num outro instante $t_1>t_0$, um dos aviões está a $y_1$ milhas do ponto P e o outro está a $x_1$ milhas do ponto P (veja a figura). Determine a taxa de variação da distância entre os aviões no tempo $t_1$. O que voce pode concluir sobre a taxa de variação da distância?
Os aviões correm risco de choque? em caso afirmativo, quanto tempo o controlador tem para fazer com que um dos aviões mude a sua trajetória?
Usando o teorema do Pitáagoras obtemos no tempo $t$
$$x(t)^2+y(t)^2=z(t)^2.$$Vamos denotar por $x', y'$ e $z'$ as derivadas com respeito ao $t$. Então derivando ambos os lados com respeito ao $t$,
$$2xx'+2yy'=2zz' \ \text{ou} \ z'=\frac{xx'+yy'}{z}=\frac{xx'+yy'}{\sqrt{x^2+y^2}}.$$Dividindo por $x$ o numerador e o denominador e substituindo $x'=600$, $y'=450$ podemos escrever
$$z'=\frac{x'+(y/x) \cdot y'}{\sqrt{1+(y/x)^2}}=\frac{600+(y/x) \cdot 450}{\sqrt{1+(y/x)^2}}.$$No tempo $t_0$, $y(t_0)=y_0=150$, $x(t_0)=x_0=200$ e logo $y_0/x_0=3/4$. Ent\~ao
$$z'(t_0)=\frac{600+(y_0/x_0) \cdot 450}{\sqrt{1+(y_0/x_0)^2}}=\frac{600+(3/4) \cdot 450}{\sqrt{1+(3/4)^2}}=750 \ m/s.$$Observamos que usando triângulos semelhantes $y_0/x_0=y_1/x_1=3/4$. Logo
$$z'(t_0)=\frac{600+(y_1/x_1) \cdot 450}{\sqrt{1+(y_1/x_1)^2}}=\frac{600+(y_0/x_0) \cdot 450}{\sqrt{1+(y_0/x_0)^2}}=750 \ m/s.$$Então podemos concluir que a taxa de variação da distância é constante e não depende do tempo $t$.
Para chegar de $y_0$ a $P$ um avião vai demorar $150/450=1/3$ horas ou $20$ min. Para chegar de $x_0$ a $P$ o outro avião vai demorar $200/600=1/3$ horas ou $20$ min. Logo sim tem risco de choque e o controlador tem menos de $20$ min. para fazer com que um dos aviões mude a sua trajetória.
Uma escada com $13 \ m$ de comprimento está apoiada em uma parede vertical alta. No instante $t_0$, a extremidade inferior, que se encontra a $5 \ m$ da parede, está escorregando e se afastando da parede a uma velocidade de~$2 \ m/s$.
O leitor deve fazer um diagrama baseado no exemplo do texto da semana. Usando o teorema do Pitágoras obtemos $x(t)^2+y(t)^2=13^2$. Derivando ambos os lados com respeito ao $t$,
$$2xx'+2yy'=0 \quad \text{ou} \quad y'=\frac{-xx'}{y}.$$No instante $t_0$ temos que $x=5$, $x'= 2$, e $y=\sqrt{13^2-5^2}=12$. Logo
$$y'= \frac{-2\cdot 5}{12}=-\frac{5}{6}.$$Observamos que a velocidade é negativa porque a escada está escorregando para baixo.
No caso do item (b), o lado vertical do triângulo relevante, correspondente à altura em que se encontra o homem tem comprimento $8$ (veja figura abaixo). Vamos considerar $y_1(t)$ a altura em que o homem se encontra no instante $t$. Usando triângulos semelhantes temos que,
$$\frac{12}{8}=\frac{y(t)}{y_1(t)} \quad \text{ou} \quad y(t)=\frac{3}{2} y_1(t).$$Derivando ambos os lados com respeito ao $t$, obtemos
$$y'=\frac{3}{2}y_1'.$$Nesse caso, no instante $t_0$ temos, pelo primeiro item que $y'=-\frac{5}{6}$. Logo
$$y_1'= -\frac{5}{6}\cdot \frac{2}{3}=-\frac{10}{18}=-\frac{5}{9} \ m/s.$$