Integrais de Linha
Inicialmente vamos recorda este definição para o calculo do comprimento de arco de uma curva - digamos que a curva $\gamma(t):[a,b]\subset \mathbb{R}\rightarrow \mathbb{R}^2$ definida por $\gamma(t)=(x(t),y(t))$ - quando $t$ percorre o intervalo $[a,b]$ a curva percorre um certo arco na plano. O comprimento deste arco é dado por
\[L=\int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt.\]o integrando é o tamanho do vetor tangente.
Digamos que você tenha uma função $f:\omega\subset \mathbb{R}^2 \rightarrow \mathbb{R}$ definida por $z=f(x,y)$. Se o traço da curva $\gamma(t)\subset \omega$, então podemos definir a integral de linha por ser
\[\int_{\gamma}f(x,y)ds=\int_a^b f(x(t),y(t))\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt.\]Da definição percebemos que a integral de linha de um campo escalar pondera o comprimento de arco pelo valor da função $z=f(x,y)$ em cada ponto da curva $\gamma(t)=(x(t),y(t))$.
Em particular, a integral de linha de um campo escalar para o caso em que $f(x,y)=1$ para todo $(x,y)$ nos retorna apenas o comprimento de arco da curva $\gamma(t)$ quando $t\in[a,b]$.
Calcule a integral $\int_C (x^2+y^2) ds$, onde C é a região da esfera $x^2+y^2+z^2=4$ situada no primeiro octante e $y=x$.
Visualizando o problema, temos:
$x^2+y^2+z^2 =4 ; x=y$, com $x,y,z \ge 0$
Ou seja:
\[ \begin{split} 2x^2 + z^2 &= 4, \\\frac{2x^2}{4} + \frac{z^2}{2} &= 1, \\\frac{x^2}{2}+\frac{z^2}{4} &= 1 \end{split} \]Portanto, no plano $xy$, C é representada pela elipse $\frac{x^2}{2}+\frac{z^2}{4} = 1$, limitada no primeiro octante. Parametrizando a curva, encontra-se: $x=\sqrt{2}\cos(t)$, $y=x=\sqrt{2}\cos(t)$ e $z=2\sin(t)$, com $x,z \ge 0$
$\vec{r} = (\sqrt{2}\cos(t),\sqrt{2}\cos(t),2\sin(t)) $, com $0 \leq t \leq \frac{\pi}{2}$
Sabe-se que $ds = \lVert \vec{r'} \rVert$ e portanto:
\[ \rVert \vec{r'} \rVert = \sqrt{2\sin^2(t)+2\sin^2(t)+4\cos^2(t)} = \sqrt{4(\sin^2(t)+\cos^2(t)} = 2 \]Assim:
\[\begin{split} \int_C (x^2 + y^2)ds &= \int_{0}^{\frac{\pi}{2}} 2(\cos^2(t) + \cos^2(t)) \cdot 2 dt\\&= 8 \int_{0}^{\frac{\pi}{2}} \cos^2(t) dt\\&= 8 \cdot \frac{1}{2} \left[ t + \frac{\sin^2(t)}{2} \right]_{0}^{\frac{\pi}{2}}\\&= 4 \cdot \frac{\pi}{2}\\&= 2\pi \end{split} \]Dito isso vamos ao applet. O applet é composto de 3 partes
Na parte à direita podemos ver e editar a função $z=f(x,y)$, o caminho $\gamma(t)$ e o domínio da curva ou caminho.
:
Integral de um Campo Vetorial sobre uma Curva
Suponha que $\vec{F}:\Omega \subset \mathbb{R}^3 \rightarrow \mathbb{R}$ seja um campo de forças definido no aberto $\Omega$ e que uma partícula descreva um movimento em $\Omega$ com função de posição dado por $\gamma:[a,b]\rightarrow \Omega$ ($\gamma(t)$ é a posição da partícula no instante $t$). Se $\vec{F}$ for constante e a imagem de $\gamma$ um segmento, o trabalho $\tau$ realizado por $\vec{F}$ de $\gamma(a)$ até $\gamma(b)$ é, por definição, o produto escalar de $\vec{F}$ pelo deslocamento $\gamma(b)-\gamma(a)$.
Visto isso, segue natural definir o trabalho $\tau$ realizado por
\[\tau =\int_{\gamma}\vec{F}\cdot d\gamma = \int_a^b \vec{F}\left(\gamma(t)\right)\cdot \gamma'(t)dt\]Em um campo vetorial contínuo qualquer $\vec{F}:\Omega\subset \mathbb{R}^3\rightarrow \mathbb{R}^3$, $\Omega$ aberto, e uma curva $\gamma:[a,b]\rightarrow \Omega$, de classe $C^1$. Definimos a integral de linha de $\vec{F}$ sobre $\gamma$ por
\[\int_{\gamma}\vec{F}\cdot d\gamma = \int_a^b \vec{F}\left(\gamma(t)\right)\cdot \gamma'(t) dt\]:
Outra forma notação
Seja $\vec{F}(x,y,z)=P(x,y,z)\vec{i}+Q(x,y,z)\vec{j}+R(x,y,z)\vec{k}$ um campo vetorial contínuo no aberto $\Omega$ de $\mathbb{R}^3$ e seja $\gamma:\left[a,b\right]\rightarrow \Omega$ uma curva de classe $C^1$ dada por $x=x(t)$, $y=y(t)$, $z=z(t)$. Temos
\[\int_{\gamma}\vec{F}\cdot d\gamma = \int_a^b \left[P(x(t),y(t),z(t)) \vec{i} + Q(x(t),y(t),z(t))\vec{j} + R(x(t),y(t),z(t))\vec{k}\right]\cdot \left[\frac{dx}{dt} \vec{i} + \frac{dy}{dt}\vec{j} + \frac{dz}{dt} \vec{k} \right]dt\]Então,
\[\int_a^b\left[P(x(t),y(t),z(t))\frac{dx}{dt}+Q(x(t),y(t),z(t))\frac{dy}{dt}+R(x(t),y(t),z(t))\frac{dz}{dt}\right]dt\]e escrevemos esta integral de linha da seguinte forma:
\[\int_{\gamma} Pdx+Qdy+Rdz\]Calcule a integral de linha $I = \int_C ydx + (x + 2y)dy $ de $(1,0)$ à $(0,1)$ onde C é o arco de circunferência $x=\cos(t)$ e$y=\sin(t)$.
Temos :
\[ dx=-\sin(t)dt ; dy=\cos(t)dt\]Logo, a integral fica da forma:
\[\begin{split} \int_{0}^{\frac{\pi}{2}} -\sin^2(t) + \cos^2(t) + 2\sin(t)\cos(t) \end{split} \]Utilizando as identidades trigonométricas $-\sin^2(x)+\cos^2(x) = \cos(2x)$ e $2\sin(x)\cos(x) = \sin(2x)$ a integral fica da forma :
\[\begin{split} \int_{0}^{\frac{\pi}{2}} (\cos(2t) + \sin(2t))dt &= \left[ \frac{\sin(2t)}{2} + \frac{\cos(2t)}{2} \right]_{0}^{\frac{\pi}{2}}\\&= \left( \frac{0-(-1)}{2} - \frac{0 - 1}{2} \right)\\&= \frac{2}{2}\\&= 1 \end{split} \]Teorema de Green
Seja $\vec{F} = P(x,y)\hat \imath + Q(x,y)\hat \jmath$ = (P(x,y),Q(x,y)) um campo vetorial de classe $C^1$ definido em $C \in \mathbb{R}^{2}$ onde o bordo (fronteira) seja orientada positivamente(sentido anti-horário) e seja D a região delimitada por C.
Em resumo, o teorema de Green diz que uma integral de área do $\,\mathrm{rot}\,2D$ do campo vetorial é equivalente à integral de linha fechada do mesmo campo ao redor de uma superficie.
Dedução do teorema de Green
Define-se C como a união de 4 caminhos, como mostrado abaixo
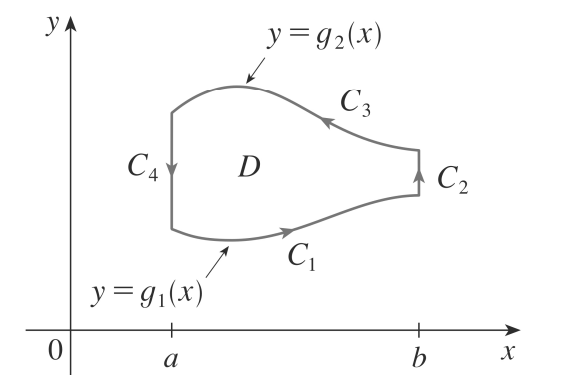
Figura do livro "cálculo", quinta edição, de James Stewart
$C_1$ pode ser descrito como: $r_1(x) = x\hat \imath + g_1(x)\hat \jmath, a \leq x \leq b$
Logo:
\[\begin{split} \int_{C_1} Pdx = \int_{a}^{b} P(x,{g_1}(x))dx \end{split} \]Analogamente
$-C_3$ pode ser descrito como $r_3(x) = x\hat \imath + g_2(x)\hat \jmath, a \leq x \leq b$
Logo:
\[\begin{split} \int_{C_3} = -\int_{C_3} Pdx = -\int_{a}^{b} P(x,{g_2}(x))dx \end{split} \]E finalmente, com relação à $C_2$ e $C_4$, x= constante e portanto, dx=0, logo:
\[\begin{split} \int_{C_2} Pdx = \int_{C_4} Pdx = 0 \end{split} \]Assim:
\[\begin{split} \int_{C} Pdx &= \int_{C_1} Pdx + \int_{C_2} Pdx + \int_{C_3} Pdx + \int_{C_4} Pdx\\&= \int_{C_1} Pdx - \int_{C_3} Pdx\\&= \int_{a}^{b} P(x,g_1(x))dx - \int_{a}^{b} P(x,g_2(x))dx\\&= -\int_{a}^{b} \left[P(x,g_2(x)) - P(x,g_1(x)) \right] dx \end{split} \]Assim, pelo teorema fundamental do cálculo
\[\begin{split} -\int_{a}^{b} \int_{g_1(x)}^{g_2(x)} \frac{\partial P}{\partial y} dydx = -\iint_D \frac{\partial P}{\partial y} dA \end{split} \]Da mesma forma, pode-se provar:
\[\begin{split} \int_C Qdy = \iint_D \frac{\partial Q}{\partial x} dA \end{split} \]Descrevendo D como:
D = ${(x,y) \in \mathbb{R}^{2} : c \leq y \leq d, h_1(y) \leq x \leq h_2(y)}$
Onde $h_1$ e $h_2$ são funções contínuas.
Por fim, combinando as duas equações encontradas:
Cálcular o trabalho realizado por $\vec{F}=(\frac{x^2=y^2}{2},\frac{x^2}{2}+y^4)$ através do bordo da região D={
$1 \leq x^2+y^2 \leq 2$ : $x \ge 0, y\ge 0$
}, orientada positivamente. Interpretando a região, observa-se que está é uma coroa circular localizada no primeiro quadrante. Passando para coordenadas polares, tem-se: $1 \leq r \leq 2$ e $0 \leq \theta \leq \frac{\pi}{2}$O teorema de green diz que: \[\begin{split} \oint_{C} Pdx + Qdy = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA \end{split} \]
Cálculando $\left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)$:
$\frac{\partial Q}{\partial x} = x$ , $\frac{\partial P}{\partial y} = -y$
A integral fica:
\[\begin{split} \iint_D \left( x - (-y) \right) dxdy \end{split} \]Passando para polares:
\[\begin{split} &=\int_{0}^{\frac{\pi}{2}} \int_{1}^{2} (r\cos{\theta} + r\sin{\theta})r dr d\theta\\&= \left[\frac{r^3}{3}\right]_{1}^{2} \int_{0}^{\frac{\pi}{2}} \cos{\theta} + \sin{\theta} d\theta\\&= \left( \frac{2^3}{3}-\frac{1^3}{3}\right) \left[ \sin{\theta} - \cos{\theta} \right]_{0}^{\frac{\pi}{2}}\\&= \frac{7}{3}((1-0)-(0-1))\\&= \frac{7}{3} \cdot 2\\&= \frac{14}{3} \end{split} \]Segue abaixo um applet do geogebra demonstrando um campo vetorial ao redor de uma curva.
:
Winding Number
O winding number ou o número de voltas ou conta giros intuitivamente é a contagem da quantidade de voltas que uma curva dá ao redor de um ponto. O objetivo deste texto é explicar como obter uma expressão analítica para este conceito.
:
Inicialmente vamos considerar o seguinte lema
Seja $f(x,y)$ uma função a valores reais definida no aberto $\Omega \subset \mathbb{R}^2$, um $I$ intervalo aberto e $a<b$ dois números reais e suponha que o retângulo
\[R=\left\{(x,y)\in \mathbb{R}^2: a\leq x\leq b, y\in I\right\}\subset \Omega.\]Suponha, além disso, que $f(x,y)$ e $\frac{\partial f}{\partial x}$ sejam contínuas em $\Omega$. Nestas condições, a função
\[\varphi(y)=\int_a^b{f(x,y)}dx,\,\,\, y \in I\]é derivável e temos que para todo $y\in I$,
\[\varphi'(y)=\int_a^b{\frac{\partial f}{\partial y}(x,y)}dx.\]Considere
Seja $\Omega$ um aberto de $\mathbb{R}^2$ satisfazendo a propriedade: existe $(x_0,y_0)\in \Omega$ tal que, para todo $(x,y)\in \Omega$, a poligonal de vértices: $(x_0,y_0)$, $(x_0,y)$ e $(x,y)$ está contido em $\Omega$. Seja $\vec{F}(x,y)=P(x,y)\vec{i}+Q(x,y)\vec{j}$, $(x,y)\in \Omega$, de classe $C^1$. Nestas condições, se $\,\mathrm{rot}\, \vec{F}=\vec{0}$ em $\Omega$, então $\vec{F}$ será conservativo.
Seja $A=\left\{(x,y)\in \mathbb{R}^2| x\geq 0 \mbox{ e } y=0\right\}$ e seja $\Omega=\left\{(x,y)\in \mathbb{R}^2| (x,y)\notin A\right\}$, isto é, $\Omega$ é o $\mathbb{R}^2$ menos o semieixo positivo dos $x$. Considere a função
\[\varphi(x,y) = \int_0^y{Q(-1,t)}dt +\int_{-1}^x{P(t,y)}dt \]onde $P(x,y)=\frac{-y}{x^2+y^2}$ e $Q(x,y)=\frac{x}{x^2+y^2}$.
É claro $(-1,0)\in \Omega$ e todo $(x,y)\in \Omega$, a poligonal de vértices: $(-1,0)$, $(-1,y)$ e $(x,y)$ está contida em $\Omega$.
Agora calculando o $\,\mathrm{rot}\, \vec{F}= \left(-\frac{\partial(Q)}{\partial y}+\frac{\partial P}{\partial x}\right)\vec{k}=\left(\frac{x^2-y^2}{\left(x^2+y^2\right)^2}-\frac{2 x y}{\left(x^2+y^2\right)^2}\right)=0\vec{k}$. Como $\vec{F}$ é de classe $C^1$ em $\Omega$, segue pelo teorema anterior que
\[\nabla \varphi =\vec{F} \mbox{ em } \Omega.\]Agora como
\[Q(-1,t)=\frac{-1}{1+t^2} \mbox{ e }P(t,y)=\frac{-y}{t^2+y^2}.\]Assim,
\[\varphi(x,y)=\int_0^y{\frac{-1}{1+t^2}} dt + \int_{-1}^x{\frac{-y}{t^2+y^2}}dt.\]Como
\[\int_0^y{\frac{-1}{1+t^2}} dt =\left[-\,\mathrm{arctg}\, t \right]_0^y=-\,\mathrm{arctg}\, y\]e
\[\int_{-1}^x{\frac{-y}{t^2+y^2}}dt =\left\{\begin{array}{lcl}\left[-\,\mathrm{arctg}\, \frac{t}{y}\right]_{-1}^y& \mbox{ se }&y\neq 0\\ 0 & \mbox{ se }& y=0 \mbox{ e }x<0\end{array} \right.\]resulta
\[\varphi(x,y)=\left\{\begin{array}{lcl}0 & \mbox{ se }& y=0 \mbox{ e }x<0\\-\,\mathrm{arctg}\, y -\,\mathrm{arctg}\, \frac{1}{y}-\,\mathrm{arctg}\, \frac{x}{y}& \mbox{ se }&y\neq 0\\ \end{array} \right.\]Observamos ainda que, para todo $y>0$,
\[\,\mathrm{arctg}\, y + \,\mathrm{arctg}\, \frac{1}{y}= \frac{pi}{2}.\]De fato, para todo $y>0$,
\[\left[\,\mathrm{arctg}\, y +\,\mathrm{arctg}\, \frac{1}{y}\right]'=0.\]logo, $\,\mathrm{arctg}\, y + \,\mathrm{arctg}\, \frac{1}{y}$ é constante em $(0,+\infty)$. Como, para $y=1$,
\[\,\mathrm{arctg}\, 1 + \,\mathrm{arctg}\, \frac{1}{y}= \frac{pi}{2}.\]conclui-se que, para todo $y>0$ a igualdade se verifica. Dá para repetir o argumento para $y<0$ e podemos concluir que
\[\,\mathrm{arctg}\, y + \,\mathrm{arctg}\, \frac{1}{y}= -\frac{pi}{2}.\]Assim,
\[\varphi(x,y)=\left\{\begin{array}{lcl}-\frac{\pi}{2}-\,\mathrm{arctg}\, \frac{x}{y} & \mbox{ para }& y>0 \\0& \mbox{ para }& y=0 \mbox{ e }x<0 \\\frac{\pi}{2}-\,\mathrm{arctg}\, \frac{x}{y}& \mbox{ para }&y<0.\\ \end{array} \right.\]Observe ainda que $\Theta(x,y)=\varphi(x,y)+\pi$ é, também, uma função potencial para $\vec{F}$ em $\Omega$.
\[\Theta(x,y)=\left\{\begin{array}{lcl}\frac{\pi}{2}-\,\mathrm{arctg}\, \frac{x}{y} & \mbox{ para }& y>0 \\\pi& \mbox{ para }& y=0 \mbox{ e }x<0 \\\frac{3\pi}{2}-\,\mathrm{arctg}\, \frac{x}{y}& \mbox{ para }&y<0.\\ \end{array} \right.\]Vamos verificar que $\Theta(x,y)$ é o ângulo que a semireta $\left\{(tx,ty)| t\geq 0\right\}$ forma com o semieixo positivo dos $x$.
Para verifica isso, precisamos dividir em casos, um deles seria $x>0$ e $y>0$. Neste caso,
\[\Theta(x,y)=\frac{\pi}{2} - \,\mathrm{arctg}\,\frac{x}{y}\]ou
\[\frac{x}{y} = \,\mathrm{tg}\,\left(\frac{\pi}{2}-\Theta(x,y)\right)= \frac{1}{\,\mathrm{tg}\, \Theta(x,y)}\]e, portanto,
\[\frac{y}{x} = \,\mathrm{tg}\,{ \Theta(x,y)}.\]Faça para os outros casos. Podemos denominar $\Theta(x,y)$ a função ângulo. Você já pode imaginar como seria o gráfico da função $\Theta(x,y)$.
Voltemos agora a discussão inicial queremos determinar uma forma analítica para contar a quantidade de voltas, no sentido anti-horário, que uma curva dá ao redor de um ponto $(x_0,y_0)$. Para muitas curvas tais como:
\[\alpha(t) = (x_0 +a \cos t, y_0+ a \,\mathrm{sen} \, t),\,\, t\in[0,2\pi]\]é intuitivo contar qual seria o números de voltas. Também é claro que se substituirmos $t$ por $-t$ nós obtemos um número negativo, pois neste caso a curva percorre no sentido horário. Apesar de ser intuitivo este calculo, não conseguimos implementar esta conta no computador, para isso precisamos de uma definição analítica.
Considere $\gamma(t)=(x(t),y(t))$ com $a\leq t \leq b$ uma curva suave e seja $P_0=(x_0,y_0)$ por ser um ponto que não esta na curva $\gamma(t)$, então o número de voltas de $\gamma(t)$ dá em torno do ponto $P_0$ é denotado por $W(\gamma, P_0)$ pela seguinte integral
\[W(\gamma, P_0) = \frac{1}{2\pi}\int_a^b{\frac{\left[x(t)-x_0\right]y'(t)-\left[y(t)-y_0\right]x'(t)}{\left[x(t)-x_0\right]^2+\left[y(t)-y_0\right]^2}}dt.\]Isto é o mesmo que a integral de linha
\[\frac{1}{2\pi} \oint_{\gamma} \!{\frac{-(y-y_0)}{(x-x_0)^2+(y-y_0)^2}dx+\frac{(x-x_0)}{(x-x_0)^2+(y-y_0)^2}dy}.\]A consistência da definição segue imediatamente da análise do exemplo.

