Integral tripla sobre uma região do espaço
Visualização da região $ W= \{(x,y,z) \; | \; a \leq x \leq b\;\;\; g_1(x) \leq y \leq g_2(x) , \;\; \; h_1(x,y) \leq z \leq h_2(x,y) \} $ , essa região pode ser entendida como uma região do tipo I no espaço sobre uma região de tipo I no plano. Temos uma estimativa numérica da função $f$ definida sobre $W$.
:
Sólido em Coordenadas Cilíndricas
Da mesma forma que é necessário utilizar uma substituição de variáveis para calcular a integral de regiões circulares em $\mathbb{R}^{2}$, existem duas possíveis mudanças de variáveis no $\mathbb{R}^{3}$. A primeira esta ligada com a parametrização do cilindro em $\mathbb{R}^{3}$. Considere a superfície definida por $x^2+y^2=5$:
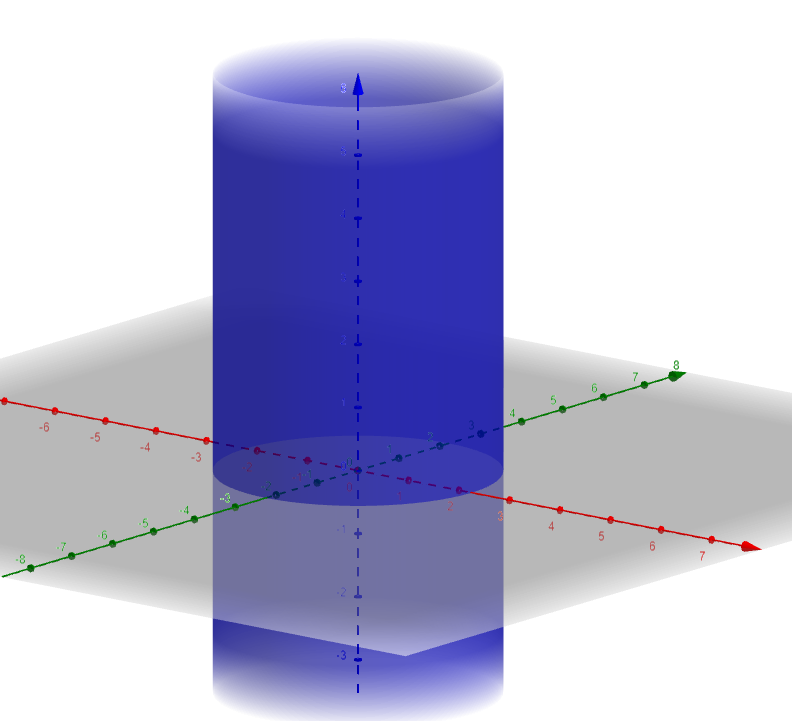
Mais geralmente, considere um cilindro sólido $x^2+y^2\leq R^2$, com $R\geq 0$. Podemos parametrizar esta região com a aplicação: $x=r \cos \theta $, $y=r \,\mathrm{sen} \, \theta $ e $z=z$. Que toma a região do $\mathbb{R}^3$: $0\leq r \leq R$, $0 \leq \theta \leq 2\pi$ e $z \in \mathbb{R}$ e mapeia no cilindro sólido.
As coordenadas cilíndricas nos lembra as coordenadas polares no plano.
Observe que os pontos nos quais tal transformação esta definida não é injetora, apesar disso o conjunto dos pontos nas quais esta transformação não é injetora é um conjunto de medida nula. Além disso, nos pontos interiores a transformação tem o Jacobiano dado por
J= $\frac{\partial(x,y,z)}{\partial(r,\theta,z)}$ = $\det\begin{bmatrix} \cos \theta & \,\mathrm{sen} \, \theta & 0\\ -r\,\mathrm{sen} \, \theta & r\cos \theta & 0\\ 0 & 0 & 1 \end{bmatrix} = r$
Observe como o jacobiano é o mesmo tanto para as coordenadas polares do $\mathbb{R}^2$ quanto para cilíndricas.
Applet abaixo demonstrando como as coordenadas cilíndricas se comportam:
:
Calculando o volume de um cilindro
Vamos utilizar a mudança de coordenadas sugerida acima para determinar o volume $V$ de um cilindro, com $z$ entre $Z_i$ à $Z_f$,
\[\begin{split} \int_{Z_i}^{Z_f} \int_{0}^{2\pi} \int_{0}^{R} 1\cdot r \,\, dr\, d\theta \, dz= (Z_f-Z_i) \cdot R^2 \cdot \pi \end{split} \]Assim se deduzimos a fórmula do volume de um cilindro, que confirma a nossa intuição.
Considere região $W$ limitada pelo paraboloide $z=x^2+y^2$ e pelo cone $z=\sqrt{x^2+y^2}$ no primeiro quadrante: $x \geq 0$ e $y \geq 0$. Calcule a integral de $f(x,y,x)=(x^2+y^2)^9$ nesta região.
:
Ao tentarmos determinar a região de interseção do paraboloide e do cone obtemos uma equação de ordem 4 (uma quártica). Uma maneira mais simples de obtermos esta interseção é considerar a mudança de coordenadas $x=r \cos(\theta)$, $y=r \,\mathrm{sen} \,(\theta)$ e $z=z$, com isso obtemos $z=r^2=r \Leftrightarrow r^2-r=0$ se, e somente se, $r=1$ ou $r=0$. Para $r=0$ temos o ponto $(0,0,0)$ em comum, para $r=1$ temos que a interseção é uma circunferência de raio 1 na altura $z=1$.
Continuando com as coordenadas cilíndricas: $r^2 \leq z \leq r$, como a região se limita no primeiro quadrante, teremos $0 \leq \theta \leq \frac{\pi}{2}$, por fim, $0 \leq r \leq 1$.
\[\begin{split} \iiint_W{f(x,y,z)}&=\int_{0}^{\frac{\pi}{2}} \int_{0}^{1} \int_{r^2}^{r} (r^2)^9 \cdot r \,\,dr\,d\theta\, dz\\&=\frac{\pi}{2} \int_{0}^{1} \int_{r^2}^{r} r^{19} dz\,dr\\&=\frac{\pi}{2}\int_{0}^{1} r^{19}(r-r^2)dr\\&=\frac{\pi}{2}\left[\frac{r^{21}}{21}-\frac{r^{22}}{22}\right]_{0}^{1}\\&=\frac{\pi}{2}\left(\frac{1}{21}-\frac{1}{22}\right)\\ \end{split} \]Sólido em coordenadas esféricas
A outra mudança de coordenada a se considerar vem da parametrização da esfera $S\subset \mathbb{R}^{3}$ definida pela desigualdade $x^2+y^2+z^2=r^2$, de raio $r>0$. Que pode ser parametrizada por $x=r \sin(\phi)\cos(\theta)$, $y=r\sin(\phi)\sin(\theta)$ e $z=r\cos(\theta)$.
Graças a esta parametrização da esfera, podemos calcular integrais que em coordenadas cartesianas seriam muito difíceis. Considere um ponto $P$ que nas coordenadas cartesianas tem coordenadas $(x,y,z)$ e que nas coordenadas esféricas tem coordenadas $(\rho, \varphi, \theta)$, onde $\rho$ representa o comprimento do vetor $\vec{0P}$ e $\varphi$ representa o ângulo formado entre o vetor $\vec{OP}$ e o semi-eixo positivo $Oz$ e $\theta$ representa o ângulo formado entre $OP_1$ e o semi-eixo positivo $Ox$, onde $P_1=(x,y,0)$ que é a projeção ortogonal do vetor $\vec{OP}$ sobre o plano plano XY.

O $0\leq \varphi \leq \pi$ e $0\leq \theta \leq 2\pi$.
A relação entre as coordenadas é dada por:
\[ x=\rho\sin \varphi \cos \theta, \,\, y=\rho\sin \varphi \sin \theta , \,\, z=\rho\cos \varphi \]que mapeia a região $B = \left\{(\theta, \rho, \varphi)\in \mathbb{R}^3: 0\leq \theta \leq \pi,\,\, \rho\geq 0,\,\, 0\leq \varphi \leq \pi\right\}$. em $\mathbb{R}^3$. Reciprocamente, podemos determinar $\rho$, $\varphi$ e $\theta$ por
\[\rho^2=x^2+y^2+z^2,\,\, \,\mathrm{tg} \,(\varphi)=\frac{r}{z}, \,\, \,\mathrm{tg} \,(\theta)=\frac{x}{y} \mbox{ onde } r=\sqrt{x^2+y^2}.\]O Jacobiano das coordenadas esféricas
Por definição o jacobiano é dado por
\[\begin{split} \frac{\partial(x,y,z)}{\partial(\theta,\rho,\varphi)} &= \det \begin{bmatrix} -\rho \,\mathrm{sen} \, \varphi \,\mathrm{sen} \, \theta & \,\mathrm{sen} \, \varphi \cos \theta & \rho \cos \varphi \cos \theta\\\rho \,\mathrm{sen} \, \varphi \cos \theta & \,\mathrm{sen} \, \varphi \,\mathrm{sen} \, \theta & \rho \cos \varphi \,\mathrm{sen} \, \theta\\0 & \cos \phi & -\rho \,\mathrm{sen} \, \varphi \end{bmatrix} \\&= \rho^2 \,\mathrm{sen} \, \varphi \cdot \det \begin{bmatrix} -\,\mathrm{sen} \, \theta & \,\mathrm{sen} \, \varphi \cos \theta & \cos \varphi \cos \theta\\\cos \theta & \,\mathrm{sen} \, \varphi \,\mathrm{sen} \, \theta & cos \varphi \,\mathrm{sen} \, \theta\\0 & \cos \varphi & - \,\mathrm{sen} \, \varphi \end{bmatrix} \\&=\rho^2\,\mathrm{sen} \, \varphi.\\ \end{split} \]Observe que o jacobiano só será zero se $\rho^2\,\mathrm{sen} \, \varphi=0$ se $\rho=0$ ou $\varphi= 0 $ ou $\pi$. Além disso, $B$ é um conjunto compacto, com fronteira de conteúdo nulo. E os pontos que o jacobiano se anula estão na fronteira de $B$
Integrais triplas em coordenadas esféricas
Cálcule $\iiint_W \left(x^2+y^2+z^2\right)\,\,dV$ sendo $W$ a região limitada superiormente pela esfera $x^2+y^2+z^2=16$ e inferiormente pelo cone $z=\sqrt{x^2+y^2}$.
Solução:
Fazendo a interseção das duas superfícies encontramos:
\[x^2+y^2+(\sqrt{x^2+y^2})^2=16 \Leftrightarrow 2(x^2+y^2)=16, \mbox{ com } z=2\sqrt{2}.\]Logo a interseção das superfícies é uma curva contida no plano $z=2\sqrt{2}$ e sua projeção no plano $XY$ forma um círculo de raio $2\sqrt{2}$.
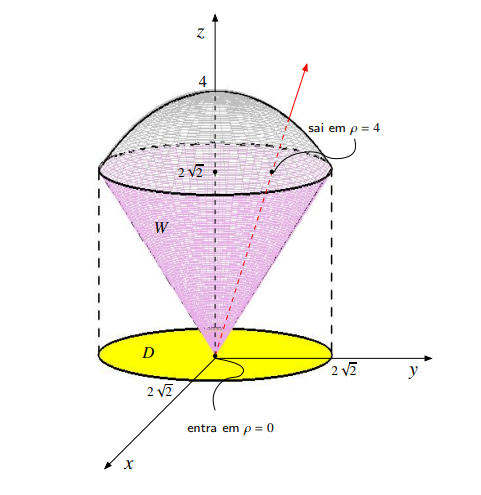
Passando para coordenadas esféricas: vemos que o $\varphi$ deve variar de $0$ até $\,\mathrm{arctg} \,{1}= \pi/4$.
Montando a integral temos:
\[\begin{split} \iiint_W \left(x^2+y^2+z^2 \right)\,dV &= \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{4}} \int_{0}^{4} \rho^2 \cdot \rho^2 \,\mathrm{sen} \,{\varphi} \,\,d\rho\, d\varphi\, d\theta \\&= 2\pi \int_{0}^{\frac{\pi}{4}} \int_{0}^{4} \rho^4 \,\mathrm{sen} \,{\varphi}\,\, d\rho \,d\varphi\\&= 2\pi \left[\frac{\rho^5}{5}\right]_{0}^{4} \int_{0}^{\frac{\pi}{4}} \,\mathrm{sen} \,{\varphi}\,\, d\varphi\\&= 2\pi \frac{4^5}{5} \left[-\cos \varphi \right]_{0}^{\frac{\pi}{4}}\\&= \frac{2 \cdot 4^5 \cdot \pi}{5}\left(-\frac{\sqrt{2}}{2}-(-1)\right)\\&= \frac{4^5 \cdot \pi}{5}\left(2-\sqrt{2} \right) \end{split} \]

