Superfície
Podemos considerar uma integral de superfície como o equivalente bidimensional da integral de linha, sendo a região de integração uma superfície em vez de uma curva. Antes que possamos estudar de maneira compreensível o que são as integrais de superfície, temos que estar de acordo sobre o que devemos entender por uma superfície. Grosseiramente falando, uma superfície é o lugar geométrico definido por um ponto que se move no espaço com dois graus de liberdade. Já conhecemos alguns métodos para definir tais lugares geométricos por meio de fórmulas matemáticas. Um é a representação implícita, na qual descrevemos uma superfície como um conjunto de pontos (x, y. z) verificando uma equação da forma
\[F(x, y, z)=0.\]Algumas vezes podemos escrever uma das variáveis em termos das outras. Digamos que $z$ é dado em função de $x$ e $y$. Quando isso é possível obtemos uma representação explícita, dada por uma ou mais equações da forma $z =f(x, y)$. Como no exemplo da esfera de raio 1 e centro na origem tem a representação implícita $x^2 + y ^2+ z^2 - 1 = 0$. Resolvendo em ordem a z obtemos duas soluções,
\[z=\sqrt{1-x^2-y^2} \mbox{ e } z=-\sqrt{1-x^2-y^2}.\]A primeira nos fornece uma representação explícita da ·semi-esfera superior e a segunda uma representação do mesmo tipo para a semi-esfera inferior: Existe um terceiro método de representação de superfícies, o qual é de maior utilidade no estudo dqs integrais de superfície; trata-se da representação vectorial ou paramétrica, na qual três equações exprimem $x$, $y$ e $z$ em função de dois parâmetros $u$ e $v$
\[x = x(u, v), \,\,\, y = y(u, v),\,\,\, z = z(u, v).\]Aqui o ponto $(u, v)$ é permitido variar sobre um conjunto conexo bidimensional $T$ do plano $U0V$, e os correspondentes pontos (x, y, z) constituem uma porção de superfície no espaço $XYZ$. Este método de descrição de uma superfície é análogo à representação de uma curva, no espaço, por intermédio de três equações paramétricas a um parâmetro. Tudo isso podemos colacar na forma
\[r(u, v) = (x(u, v), y(u, v), z(u, v)), \mbox{ com } (u, v) \in T.\]Existem, naturalmente, muitas representações paramétricas para a mesma superfície. Podemos sempre obter uma delas a partir da forma explícita $z=f(x,y)$ fazendo
\[x(u,v)=u, \,\,\, y(u,v)=v,\,\,\, z(u,v)=f(u, v).\]Por outro lado, se for possível resolver as duas primeiras equações em relação a $u$ e $v$ em função de $x$ e $y$ e substituímos na terceira obtemos a representação explícita $z=f(x, y)$.
Considere a esfera de centro na origem e raio $a$. Através de nossas observações podemos obter a parametrização de por exemplo da calota sul da esfera. Fazendo em $z=-\sqrt{a^2-x^2-y^2}$ $x=u$, $y=v$ e teremos
\[r(u,v)=(u, v,-\sqrt{a^2-u^2-v^2}),\]onde o domínio $T$ é o conjunto $(u,v)$ tais que $u^2+v^2=a^2$.
Mas continuemos examinando a esfera de centro na origem e raio $a$. Se interceptarmos a esfera com o plano $xz$, isto é, fazendo $y=0$ obtemos uma curva, a qual podemos parametrizar $\alpha(v)=(a\cos v,0, a \,\mathrm{sen} \, v)$, com $v\in (-\pi,\pi)$. Agora vamos rodar esta curva em torno do eixo z. A altura é a mesma $a \,\mathrm{sen} \, v$, e o raio $a \cos v$. Então temos
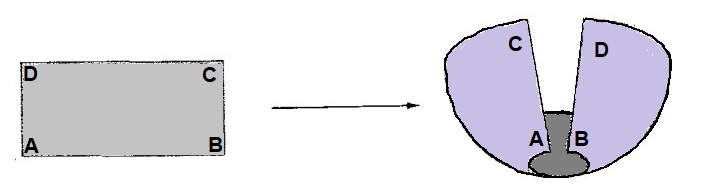
\[r(u,v)= (a\cos v \cos u, a\cos v \,\mathrm{sen} \, u, a \,\mathrm{sen} \, v ),\]onde, $T$ é o retângulo, isto é, $(u,v)$ tais que $0 \leq u \leq 2\pi$ e $-\pi \leq v \leq \pi$. O hemisfério sul é a imagem do rectângulo $[0, 2\pi] \times [-\pi, 0]$ é o retângulo inferior do rectângulo $[0, 2\pi] \times [-\pi, \pi]$. A figura nos fornece uma ideia de como o rectângulo $[0, 2\pi] \times [-\pi, 0]$ é aplicado no hemisfério sul. Imagmemos que o retângulo era construido em material plástico flexível capaz de esticar ou encolher. A figura mostra o retângulo a ser deformado numa semi-esfera. A parte superior do retângulo $AB$ transforma-se aqui no equador, os lados apostos $AD$ e $BC$ são levados à coincidência, e a base $AB$ degenera num ponto (o polo sul).
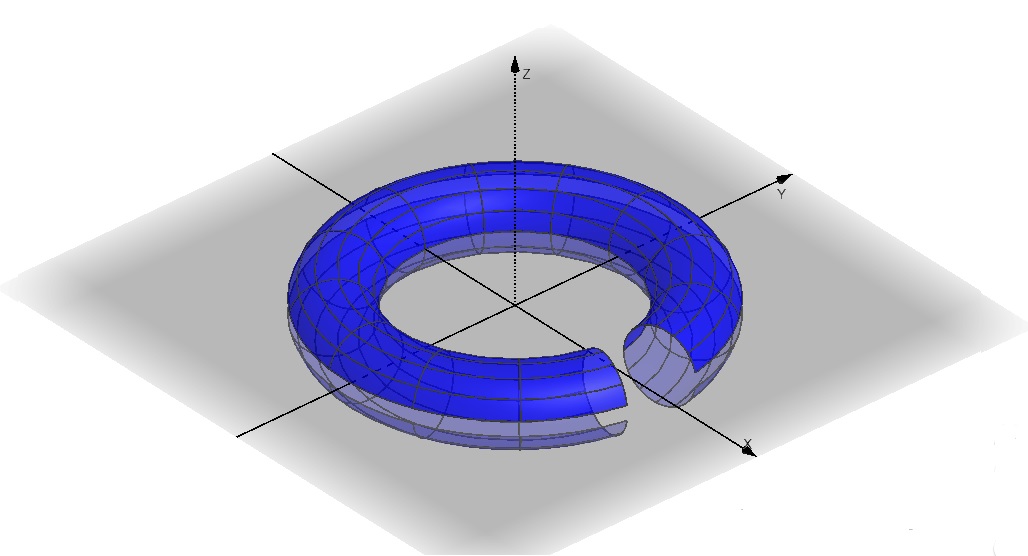
Seja $\alpha(u)=(a+r \cos u, 0, r \,\mathrm{sen} \, u)$, $u\in \mathbb{R}$, onde $0<a<r$, a curva que descreve o círculo contido no plano $x0z$, centrado no ponto $(a,0,0)$, de raio $r$. Considere a rotação de $\alpha$ e torno do eixo $z$, obtemos a superfície de rotação
\[r(u,v)=\left(\left(a+r\cos u\right)\cos v,\left(a+r\cos u\right)\,\mathrm{sen} \, v, r \,\mathrm{sen} \, v\right), \]com $(u,v)\in \mathbb{R}^2$ que descreve o toro. Imagmemos que o retângulo $T$: $0\leq u\leq 2 \pi$ e $0\leq v \leq 2\pi$ é construido em material plástico flexível capaz de esticar ou encolher. A figura abaixo sugere como o retângulo deve ser deformado no toro. A parte superior do retângulo transforma-se aqui na parte de cima do toro, os lados apostos são levados à coincidência, e a base volta a coincidir quando u alcançar o valor de $2\pi$.
Considere a superfície, conhecida como Faixa de Möibus, cuja expressão $(x,y,z)=r(u,v)$, $0\leq u \leq 2\pi$ e $-1\leq v \leq 1$, dada da seguinte forma: para cada $u$ fixo, $(x,y,z)$ descreve o segmento de comprimento 2, com centro no ponto $(\cos u,\,\mathrm{sen} \, u, 1)$, localizado no plano determinado pelo eixo $z$ e pelo ponto $(\cos u, \,\mathrm{sen} \, u, 0)$ e que forma com o eixo $z$ um ângulo $\frac{u}{2}$.
Inicialmente vamos parametrizar o segmento $AB$. Pelo expresso o centro do segmento é dado em função de $u$ por $P=(\cos u, \,\mathrm{sen} \, u, 1)$ e $B=\left(\left(1+\,\mathrm{sen} \,\frac{u}{2}\right)\cos u,\left(1+\,\mathrm{sen} \,\frac{u}{2}\right)\,\mathrm{sen} \, u ,1+\cos \frac{u}{2}\right)$. Disso segue que a parametrização do segmento $AB$ é dado por:
\[(x,y,z)=P+v(B-P),\,\,-1\leq v \leq 1,\]ou seja,
\[(x,y,z)=(\cos u, \,\mathrm{sen} \, u, 1)+v\left(\,\mathrm{sen} \, \frac{u}{2}\cos u, \,\mathrm{sen} \, \frac{u}{2}\,\mathrm{sen} \, u, \cos \frac{u}{2}\right).\]Portanto a expressão de $r(u,v)$ é dada por
\[\left\{\begin{array}{rcl}X(u,v)&=&\left(1+v \,\mathrm{sen} \, \frac{u}{2}\right) \cos u\\Y(u,v)&=&\left(1+v \,\mathrm{sen} \, \frac{u}{2}\right) \,\mathrm{sen} \, u, \mbox{ com }0\leq u \leq 2\pi,\,\, -1\leq v \leq 1. \\Z(u,v)&=& 1+v \cos \frac{u}{2}\\\end{array} \right.\]
Vetor Normal e Plano Tangente
Consideremos uma superfície definida pela equação vectorial
\[r(u, v) = (x(u, v),y(u, v), z(u, v)),\mbox{ com }(u,v)\in T.\]Se $X$, $Y$ e $Z$ são diferenciáveis em $T$, consideremos os dois vetores:
\[\begin{array}{rcl}\frac{\partial r}{\partial u}&=&\frac{\partial x}{\partial u}+\frac{\partial y}{\partial u}+\frac{\partial z}{\partial u};\\\frac{\partial r}{\partial v}&=&\frac{\partial x}{\partial v}+\frac{\partial y}{\partial v}+\frac{\partial z}{\partial v}.\\\end{array}\]O chamaremos o produto vetorial, $\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}$ de produto vetorial fundamental da representação $r$. As suas componentes podem ser expressas por intermédio de determinantes de matrizes jacobianas. Com efeito, temos
\[\begin{aligned} \frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}&= \det \begin{bmatrix} \vec{i} & \vec{j} & \vec{k}\\ \frac{\partial x}{\partial u}&\frac{\partial y}{\partial u}&\frac{\partial Z}{\partial u}\\\frac{\partial x}{\partial v}&\frac{\partial y}{\partial v}&\frac{\partial Z}{\partial v} \end{bmatrix} \\&=\det\begin{bmatrix} \frac{\partial y}{\partial u}&\frac{\partial z}{\partial u}\\\frac{\partial y}{\partial v}&\frac{\partial z}{\partial v} \end{bmatrix} \vec{i}+\begin{bmatrix} \frac{\partial z}{\partial u}&\frac{\partial x}{\partial u}\\\frac{\partial z}{\partial v}&\frac{\partial x}{\partial v}\\ \end{bmatrix} \vec{j} + \begin{bmatrix} \frac{\partial x}{\partial u}&\frac{\partial y}{\partial u}\\\frac{\partial x}{\partial v}&\frac{\partial y}{\partial v} \end{bmatrix} \vec{k}\\&= \frac{\partial(y,z)}{\partial (u,v)}\vec{i}+ \frac{\partial(z,x)}{\partial (u,v)}\vec{j}+\frac{\partial(x,y)}{\partial (u,v)}\vec{k}. \end{aligned} \]Se $(u, v)$ é um ponto de $T$ no qual $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ são contínuas e o produto vetorial fundamental é não nulo; então o ponto imagem $r(u, v)$ é chamado ponto regular de $r$. Pontos nos quais $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ não são contínuos, ou em que $\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v} = 0$ são ditos pontos singulares de $r$. Uma superfície $r$ é dita regular se todos os seus pontos o forem. Toda a superfície admite mais do que uma representação paramétrica (veja o exemplo da esfera). Pode acontecer que em uma parametrização (ver o exemplo dos polos da esfera) uma superfície pode ser regular para uma determinada representação, mas singular noutra. O significado geométrico de pontos regulares e singulares pode ser explicar do modo seguinte: Consideremos em $T$ um segmento de reta horizontal. A sua imagem por $r$ é uma curva (chamada a curva $u$) pertencente à superfície $r$ ( Para um $v$ fixo, consideremos o parâmetro $u$ como representando o tempo. O vetor $\frac{\partial r}{\partial u}$ é o vetor velocidade ao longo desta curva. Quando $u$ varia de $\Delta u$, um ponto inicialmente situado em $r(u, v)$ deve mover-se ao longo de uma curva $u$ de uma distância aproximadamente igual a $\left\|\frac{\partial r}{\partial u}\right\|\Delta u$, uma vez que $\left\|\frac{\partial r}{\partial u}\right\|$ representa a velocidade do ponto ao percorrer a curva $u$. Analogamente, para $u$ fixo, um ponto da curva $v$ deve deslocar-se, durante o intervalo de tempo $\Delta v$, de uma distância aproximadamente igual a $\left\|\frac{\partial r}{\partial v}\right\|\Delta v$. Um retângulo de $T$ com área $\Delta u\Delta v$ transforma-se numa porção de $r(T)$ que aproximaremos por um paralelogramo determinado pelos vetores $\frac{\partial r}{\partial u}\Delta u$ e $\frac{\partial r}{\partial v}\Delta v$. A área do paralelogramo determinado por $\frac{\partial r}{\partial u}\Delta u$ e $\frac{\partial r}{\partial v}\Delta v$ é o módulo do respectivo produto vetorial,
\[\left\|\frac{\partial r}{\partial u}\Delta u \times \frac{\partial r}{\partial v}\Delta v\right\| = \left\|\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}\right\|\Delta u \Delta v\]Deste modo a grandeza do produto vetorial fundamental pode ser considerado como um fator de ampliação de áreas. Nos pontos em que este produto vetorial é nulo o paralelogramo degenera numa curva ou num ponto. Em todo o ponto regular os vetores $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ determinam um plano cujo eixo é o vetor $\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}$.
É possível demonstrar que $\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}$ é normal a toda a curva regular da superfície; por este motivo o plano definido por $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ é chamado de plano tangente à superfície. A continuidade de $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ implica a continuidade de $\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}$; esta, por sua vez, significa que o plano tangente varia continuamente para uma superfície regular. Vemos assim que a continuidade de $\frac{\partial r}{\partial u}$ e $\frac{\partial r}{\partial v}$ evita a ocorrência de arestas, ou pontos na superfície; o não anulamento de $\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}$ assegura a não existência dos casos degenerados antes citados.
Integral de Superfície
Seja $S = r(T)$ uma superfície paramétrica representada por uma função vectorial $r$ definida na região $T$ do plano $OUV$.Como já discutimos a norma do vetor $\frac{\partial r}{\partial u} \times \frac{\partial r}{\partial v}$ pode ser interpretada como um fator de ampliação de áreas. Um retângulo em $T$ de área $\Delta u \Delta v$ é transformado por intermédio de $r$ num paralelogramo curvilíneo de $S$ com área aproximada- mente igual a
\[\left\|\frac{\partial r}{\partial u}\Delta u \times \frac{\partial r}{\partial v}\Delta v\right\|.\]A área de $S$ representada por $a(S)$, é definida pela integral dupla
\[a(S) = \iint_T{ \left\|\frac{\partial r}{\partial u}\times \frac{\partial r}{\partial v}\right\|}du dv.\]

