As curvas paramétricas são representações matemáticas de objetos no espaço. Em vez de descrever uma curva em termos de uma ou duas variáveis como, por exemplo, na equação cartesiana de uma reta:
\(2x+3y=4\)
usamos parâmetros para definir as coordenadas de um ponto ao longo da curva. Então obtemos as coordenadas paramétricas ou parametrização da reta:
\begin{cases} x(t) &= 2-3t \\ y(t) &= 2t\end{cases} \quad ,\,t\in \mathbb{R}
Essas coordenadas são chamadas de equações paramétricas da reta. Ou, diretamente, parametrização da reta. As vezes, essa parametrização é representada em forma vetorial:
X(t)=(2-3t, 2t), \;t\in \mathbb{R}
Se essas equações descrevessem o movimento de um objeto, as equações paramétricas dariam a posição do objeto no intante t. A trajetória do objeto seria a reta em si.
Bem simples!!
Dada a reta \(2x+3y=4,\) calculamos o vetor normal \(\quad \vec{n}=(2,3),\quad\) cujas coordenadas são os coeficientes que acompanham às veriáveis x e y.
Assim, um vetor diretor da reta seria \(\quad \vec{v}=(-3,2),\quad \) por ser ortogonal ao vetor normal.
Substituindo y=0 na equação cartesiana, obtemos o ponto P(2,0) por onde passa a reta. Portanto, a equação vetorial da reta é \(\quad \vec{r}(t)=(2,0)+(-3,2)t,\quad t\in \mathbb{R}\)
Fazendo \(\quad (x,y,z)=(2,0)+(-3,2)t,\quad\) obtemos as equações paramétricas desejadas:
\begin{cases} x(t) &= 2-3t \\ y(t) &= 2t\end{cases} \quad ,\,t\in \mathbb{R}
Ou equivalentemente, \(\quad X(t)=(2-3t, 2t),\;t\in \mathbb{R}\)
Legal, né?
Entre em contato com os monitores se ainda estiveres com dúvidas.
Força!
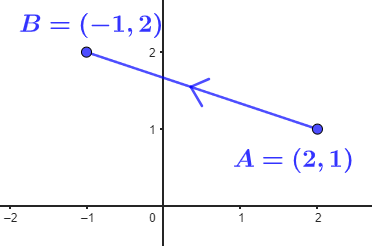 Quais seriam as equações paramétricas ou parametrização do segmento de reta que une o ponto inicial A(2,1) e o ponto final B(-1,2)?
Quais seriam as equações paramétricas ou parametrização do segmento de reta que une o ponto inicial A(2,1) e o ponto final B(-1,2)?